非线性能量阱系统的强调制响应研究

柴凯 李爽 楼京俊 朱石坚

摘要：为了得到谐波激励下本质非线性能量阱系统出现强调制响应的充要条件，开展非线性能量阱系统的强调制响应研究.利用复变量平均法推导主共振下系统的慢变动力流方程；结合多尺度法实现系统快、慢变流形的分离，得到不同参数下系统的慢不变流形以及全局分岔特性；通过构建快变流形的一维映射函数，揭示非线性能量阱系统呈现强调制响应状态的充要条件；搭建非线性能量阱系统的模拟电路，进行强调制响应检测电路试验.仿真和试验结果表明，强调制响应是由耦合系统慢变动力流中极限环的鞍结分岔引起的且真实存在，系统出现稳定的强调制响应必须满足两个条件：一是非线性能量阱系统响应超越慢不变流形上的极值点，又不吸引至慢不变流形某一分支；二是形成连续跳跃环路而不陷入局部循环时.

关键词：非线性能量阱；强调制响应；非线性动力系统；复变量平均法；振动控制

中图分类号：O322 文献标志码：A

Investigation on Strongly Modulated Response of Nonlinear Energy Sink System

CHAI Kai，LI Shuang，LOU Jingjun，ZHU Shijian

（College of Naval Architecture and Ocean，Naval University of Engineering，Wuhan 430033，China）

Abstract：In order to obtain the necessary and sufficient conditions for the strongly modulated response （SMR）of a nonlinear energy sink （NES）system under harmonic excitation，the SMR study of the NES system is carried out. Firstly，the equation of systematic slow variation flow is derived by using the complex-averaging method. Secondly，the multi-scale method is used to realize the separation of the rapid variable manifold and the slow variable manifold. And the systematic slow invariant manifold under the different parameters and the global bifurcation property are obtained. Then，by building the one-dimensional mapping function of the rapid variable manifold，the sufficient and necessary conditions for the NES system in the SMR state are revealed. Finally，the simulation circuit of the NES system is constructed，and the response detection circuit test is carried out. The simulation and experimental results show that the SMR is caused by the saddle-node bifurcation of limit cycles in the slowly varying power flow of the coupling system，and it is an actual phenomenon in engineering. The system in which SMR state can appear must satisfy the following two conditions：the response of the NES system exceeds the amplitude of the extremum point on the slow invariant manifold，but it does not attract to a branch of the slow invariant manifold，and a continuous jump loop without falling into a local cycle is formed.

Key words：nonlinear energy sink（NES）；strongly modulated response（SMR）；nonlinear dynamical systems；complex-averaging method；vibration control

非線性能量阱（Nonlinear Energy Sink，NES）是指刚度近似为立方刚度用于振动控制的非线性振子，它在一定条件下会出现靶能量传递现象.与传统线性吸振器相比，NES能有效增加吸振带宽，大幅提升减振效率，目前在航空航天[1]、房屋桥梁抗震[2]、能量采集[3]以及振动噪声控制[4]等领域得到了广泛的应用.在受外加激励作用的耦合NES系统中，由于非线性参数的作用，系统会呈现几种具有明显差异的响应形式，即周期、弱调制、强调制和混沌响应.广义上前3种类型均属于稳态响应，但其对应相轨迹具有明显差异，使得NES的振动抑制效果也具有很大的不同[5].

NES因其宽频控制的特性引起了相关学者的广泛关注.Jiang等[6]研究了正弦激励作用下，NES在较宽频带从线性振子吸收能量，且不论向前还是向后扫频，均能实现能量定向传递.Zhang等[7]研究了主结构受正弦周期力、多约束下碰撞非线性系统的能量传递问题，指出当激励幅值达到一定阈值时，能量会向NES振子聚积，而且根据激励幅值不同，系统会呈现周期、弱调制、强调制等多种具有明显差异的响应形式.Starosvetsky等[8]通过相轨迹法给出了系统响应类型与平衡点之间的关系，指出系统慢变方程对应周期解是否分岔是NES振子实现靶能量传递的关键.Gourdon等[9]研究了NES系统的强调制响应（Strongly Modulated Response，SMR），给出了系统产生强调制响应的条件，通过对比说明了NES的减振效果在非周期响应时要比稳态周期响应更好.李爽等[10]采用柔性铰链结构提出了一种NES构造方法，分析了简谐激励下耦合系统的局部分岔特性.张也弛等[11]通过数值方法研究了两自由度NES系统在简谐激励下的力学特性与抑振效果.由于强调制响应下NES系统的振动抑制效率比稳态振动更优越，因此有必要对系统产生强调制响应的充要条件作进一步研究.

本文从近似解析计算角度出发，重点研究NES系统的强调制响应.利用复变量平均法推导主共振下系统响应幅值的慢变动力流方程，深入探讨NES 系统产生强调制响应的充要条件，通过电路仿真和试验验证理论分析的正确性和强调制响应的真实性，从而间接证明NES振子在简谐激励能否实现靶能量传递.

1NES系统的慢不变流形

1.1动力学建模

如图1所示，建立机械设备耦合非线性能量阱的两自由度非线性吸振系统动力学模型（以下简称NES系统）.机械设备主系统中m₁为待减振机械设备，通过线性刚度弹簧k₁、阻尼λ₁与刚性基座连接；NES子系统安装于机械设备上层并与其耦合连接，其组成元素包括质量m₂、刚度k₂以及阻尼λ₂；f_b=F cos ΩT为作用于机械设备上的外界激励信号，F为激励力幅值，Ω为激励力频率，机械设备和NES产生的垂向位移分别为z₁和z₂.本文主要研究具有本质非线性的立方刚度型NES，故其非线性弹簧回复力为f_NES=k₂（z₂-z₁）³.

相应的动力学方程为：

采用复变量平均法推导系统的慢变动力流方程.以质量比ε为小参量，引入长度量纲l₀=m₁g/k₁，l₀对应线性弹簧k₁在重量G₁=m₁g作用下的静态形变量，并作如下无量纲变换：

将式（2）代入式（1）可得：

考虑激励频率接近主系统固有频率时的1：1：1主共振响应，令ω=1+εσ，其中σ为调谐参数，用来描述内共振频率之间的接近程度.将系统振动响应分解为质心运动以及两个振子之间的相对运动，对系统再次简化，引入新变量：u=x₁+εx₂，v=x₁- x₂，在不考虑主系统阻尼（即ξ₁=0）的情形下，将u和v代入式（3）可得：

1.2系统慢不变流形

引入新的时间尺度τ_k=ε_kt，k=0，1，…，并令ρ₂=ρ₂（τ₀，τ₁，…），采用多尺度法展开，并忽略高阶项，可得式（6）关于ε的前两阶方程：

考虑慢变幅值ρ₂关于快变时间尺度τ₀的近似解，对式（7）第一式进行积分，可得：

式中：R为关于τ₁尺度的任意函数.令?ρ₂/?τ₀=0，可得系统平衡点方程：

由式（9）可知，平衡点Φ（τ₁）只与τ₁有关，将复变量用模和相角表示，即Φ（τ₁）=N（τ₁）exp[jθ（τ₁）]，（N，θ）∈（R⁺×S¹），代入式（9）求模后可得：

Z（τ₁）=N²（τ₁），对应相位如下：

由图2可知，由于流形的不变性，系统慢变幅值只能沿着曲线运动，当达到折叠线N₁、N₂時，可能从一支稳定分支跳跃至另一支稳定分支，从而出现跳跃现象.此外，在折叠线N₁、N₂处可能存在鞍结分岔过程，从而形成N₁→N_u→N₂→N_d→N₁的连续跳跃环路并使系统响应慢变幅值出现周期性变化，类似于目标能量转移过程中“泵能”与“放能”现象.文献[13]将其称为强调制响应，该响应下NES系统出现靶能量传递现象，在其主共振附近会出现准周期响应，且幅值变化较为剧烈，能使NES具有优异的振动抑制效果.

2强调制响应产生的必要条件

2.1折奇点产生条件和慢不变流形相轨迹特征

式中：Φ（τ₁）=N（τ₁）exp[jθ（τ₁）].对式（12）两边取复数共轭，通过化简得到：

1）当g（N）≠0时为普通平衡点，满足如下表达式：

2）当g（N）=0时为折奇点，满足如下表达式：

式中：

选取系统参数C=4/3，ξ₂=0.2，σ=0，普通平衡点分岔情况如图3所示.由图3可知，当f变化时，系统只存在一个周期解，不稳定解位于折叠线N₁= 0.595 0、N₂= 0.989 6之间.另外，通过联合求解式（14）可得折叠线对应的激励力分岔值为f_b1= 0.241 9、f_b2= 0.989 2.

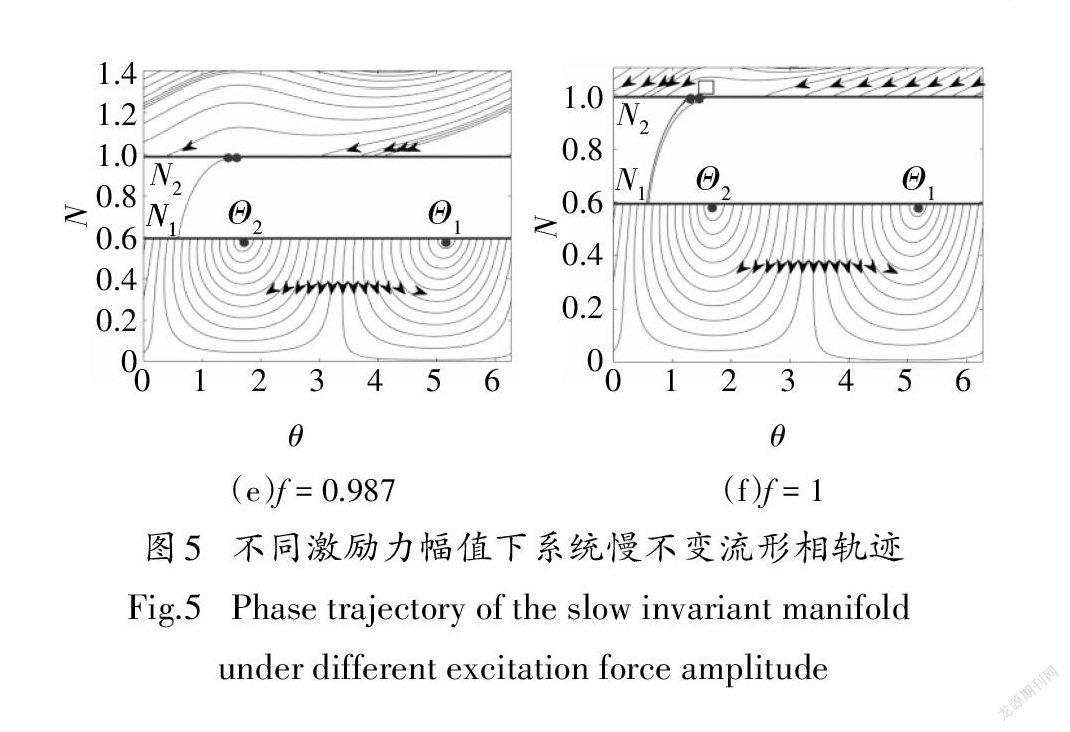
进一步求解f_ck可得折奇点对应分岔值为f_c1=0.1760、f_c2=0.9844，满足f_c1＜f_b1＜f_c2＜f_b2系统的全局分岔如图4所示，图中rp为周期吸引子，fs1、fs2分别为上、下折奇点，bp1、bp2为周期吸引子分岔点，普通平衡点与折奇点稳定性通过慢变系统线性化扰动方程的雅可比矩阵特征值判断.同时，结合Runge-Kutta数值方法与Matlab Streamline命令绘制不同激励力幅值下系统的慢不变流形，如图5所示. 图5中纵坐标为慢变幅值N，横坐标为相位θ，

由图4和图5可知，当f=0时，从N₂上方出发的相轨迹都可以回到N₂，但从N₁出发的相轨迹不能返回至N₁.与图2对比可知，相轨迹从上稳定分支出发时能跳跃至下稳定分支，而从下稳定分支出发的相轨迹不能跳跃至上稳定分支，这与实际系统也是相符合的.当不存在外界激励时，由于阻尼存在，系统能量会逐渐被耗散，直至趋于稳定.当f = 0.1时，对应f ＜f_c1，存在一个稳定的周期平衡点，不存在折奇点，所有的相轨迹都流入该吸引子.当f =f_c1时，普通平衡点出现亚临界分岔，在折叠线N₁处产生一对不稳定的下折奇点.当f = 0.18时，对应f略大于f_c1，存在一个周期平衡点与一对下折奇点（左侧下折奇点为结点，右侧下折奇点为鞍点），从鞍点右边出发的相轨迹都被吸引至周期平衡点，结点左边以及折叠线N₁右边部分出发的相轨迹吸引至结点，而结点与鞍点之间的相轨迹则有可能返回至折叠线N₁，这意味着强调制响应可能发生.当f_c1＜f＜f_b1时，存在一对不稳定的下折奇点和一个稳定的周期吸引子.当f = f_b1时，周期吸引子退化为不稳定解，同时下折奇点由不稳定变为稳定.当f = 0.5时，对应f_b1＜f ＜f_c2，系统性态发生了非常显著的变化：首先，和f = 0.18 相比，普通平衡点消失，同时鞍点与结点沿着下折叠线往两侧移动，其中结点往左侧移动，而鞍点往右侧移动，鞍结点之间的距离扩大，表明最终能回到N₁的相轨迹区域变大，同时出现强调制响应的可能性也将增加；另外，由于在绘制相轨迹过程中，相位只取一个周期（0，2π），当结点运动超过最左侧时，又重新在右端出现，此时折奇点性质已由一对鞍结点通过碰撞演化成了一对稳定的焦点.当f =f_c2时，平衡点再次出现亚临界分岔，此时演变出一对稳定的上折奇点.当f = 0.987时，对应f略大于f_c2，在上折叠线N₂出现一对鞍结点，而下折叠线N₁的一对稳定焦点依然存在，仍有可能出现强调制响应.当f=f_b2时，上折奇点由稳定退化为不稳定，同时周期吸引子再次发生Hopf分岔，由不稳定变为稳定.当f = 1时，对应f ＞f_b2，折叠线N₂上鞍结点演化成了一对不稳定的鞍点，同時在折叠线N₂附近出现了稳定的普通平衡点，此时强调制响应依然有可能出现.

2.2系统响应慢变流形

仍考虑时间尺度的前两阶，令ρ₁（t）=a₁（t）+jb₁（t）、ρ₂（t）=a₂（t）+jb₂（t），对式（5）利用多尺度法直接展开，取ε⁰阶分离实部与虚部，可得四阶常微分方程组：

对比图7中的系统响应时间历程也可验证以上分析结论，图中实线为式（5）数值计算得到的实际响应，虚线为式（16）数值计算得到的慢变幅值.由图7 可知，通过慢变方程计算得到的幅值响应与真实幅值存在一定的误差，这主要是由设定质量比为小参量条件引起的，但总体来说，预测值还是可靠的.

图8给出了C = 4/3、ξ₂= 0.2、f = 0.5、σ=0，而质量比分别为0.05、0.01和0.001时的系统响应慢变流形.质量比并不影响慢不变流形的形状，由图8可知，3种情形均能出现强调制响应，且质量比参数越小，吻合程度越高，但总体而言，通过观察慢变流形变化趋势就可判断系统是否出现了强调制响应.

总结而言，f>f_c1并不能说明系统一定会出现强调制响应，当激励频率变化时，系统响应有可能被吸引至慢不变流形的某一稳定分支或陷入局部循环，从而导致无法形成N₁→N_u→N₂→N_d→N₁的连续跳跃环路，也就不能产生强调制响应.因此，系统出现折奇点只是出现强调制响应的必要条件，仍需进一步探求系统出现强调制响应的充分条件.

3强调制响应产生的充分条件

3.1一维映射函数构建

仍考虑慢变系统，由式（15）可得N₁折叠线上折奇点对应跳跃的边界条件为Θ₁和Θ₂，令相轨迹可能从折叠线N₁跳跃至上穩定分支的相位区间为R=[Θ₁，Θ₂].考虑R→R的一维映射，若从区间R出发的相轨迹经多次N₁→N_u→N₂→N_d→N₁4个阶段后仍可返回至R，则表明慢变系统出现了稳定的极限环，强调制响应必然会发生.而系统能够产生稳定极限环的相轨迹区域则对应出现强调制响应的初始条件，这显然也是产生强调制响应的充分条件.

2）第2阶段：N_u→N₂.由于慢不变流形的确定性，从（N_u，θ_u）出发的相轨迹必然只能沿着上稳定分支运动，对式（13）积分即可得到映射终点（N₂，θ₂）.

3）第3阶段：N₂→N_d.类似于N₁→N_u的映射过程，映射表达式如下：

4）第4阶段：N_d→N₁.类似于N_u→N₂过程，从（N_d，θ_d）出发的相轨迹必然只能沿着下稳定分支运动，同样对式（13）积分即可得到映射终点（N₁，θ₁₀）.因此，可得到一维映射关系：R→R：（N₁，θ₁）→（N₁，θ₁₀）.

显然，当系统存在普通平衡点时，从R=[Θ₁，Θ₂]出发的相轨迹，有可能被吸引至慢不变流形的上下稳定分支，只有通过多次映射后映射终点仍落于R区间时，才能出现稳定的极限环，从而产生强调制响应.

3.2数值讨论与分析

当参数ε= 0.05、C = 4/3、ξ₂= 0.2、f = 0.5、σ=0时，对应Θ₁=-0.9110，Θ₂= 1.5114，各阶段映射过程如图9所示.图9（a）对应第1阶段映射过程，相轨迹从R=［Θ₁，Θ₂］出发跳跃至上稳定分支N处；图9（b）对应第2阶段映射过程，相轨迹通过上稳定分支慢变至N₂折叠线处；图9（c）对应第3阶段映射过程，相轨迹从N₂折叠线跳跃至下稳定分支；图9（d）对应第4阶段映射过程，相轨迹通过下稳定分支慢变至N₁折叠线处.由图9可知，经过一次完整的映射过程后，从R=［Θ₁，Θ₂］出发的相轨迹最终都会落在该区间内，且新得到的相位区间向内收缩，表明无论经过多少次映射，终点都会位于R=［Θ₁，Θ₂］内.因此，在该参数条件下，系统能在θ₁≈0处出现稳定的极限环.

进一步考虑在相同参数条件下，通过局部分岔得到的幅频特性曲线，如图10所示.图10中，HP_i（i=1，2，3）表示第i个Hopf分岔点；SN_j（j=1，2，3，4）表示j个鞍结分岔点.由图10可知，当σ=0时，系统不存在稳定的周期平衡点，从R=［Θ₁，Θ₂］出发的相轨迹无法被普通周期平衡点吸引，都能产生稳定的强调制响应，这也验证了一维映射的分析结果.

当σ= 2.5时，系统存在一个幅值较小的稳定周期平衡点，与σ= 0相比，其一维映射过程也发生了明显的变化，如图11所示.由图11可知，从R出发的相轨迹在第4阶段映射过程中有一部分被下稳定分支上的周期平衡点吸引，从而不能返回至R，在经过一次或多次映射过程后能够返回至R区间的映射终点较映射起始点而言整体向右偏移，表明在经过一次或多次映射过程后，系统响应将从强调制响应状态逃逸；从R区间出发的相轨迹都会逐渐吸引至稳定周期吸引子，从而不能产生稳定极限环，强调制响应也不会持续发生.

由图12可知，当超过该频率区域时，不能产生强调制响应，同时根据一维映射图可以大致判断产生强调制响应的相角范围，该相角范围代表触发强调制响应的系统初始条件；若在频率边界附近产生强调制响应的初始条件范围大大缩小，则意味着出现强调制响应的条件将会更加苛刻.

综上所述，NES系统能产生稳定的强调制响应必须满足以下条件：

2）必须形成N₁→N_u→N₂→N_d→N₁的连续跳跃环路，且轨线不被周期平衡点吸引.

显然以上两个条件对系统参数、外界激励以及初始条件都有严格的要求，特别是在多解共存区域，需要特定的初始条件才能激发稳定的强调制响应. 同时，在某些激励频率区域，系统只存在稳定的强调制响应.仍以σ=0为例，强调制响应的稳定极限环与慢变系统数值计算结果如图13所示.由图13可知：一是稳定极限环对应的初始相位为θ₁≈-0.05；二是一维映射结果与实际系统响应吻合良好，可清晰看到调制响应的两个慢变过程与两个快变过程.

4强调制响应检测电路设计与试验

采用Tina-Ti软件中模拟电路开发模块对特定参数下的NES系统进行仿真计算，并开展强调制响应检测电路试验对理论分析结论进行验证.

4.1电路原理图设计

考虑式（3）所示的动力学系统，将其改写为四维状态方程：

依据微分状态方程与电路状态方程的等价关系，强调制响应检测电路主要由积分电路、反相比例电路、乘法器等几个关键模块组成，其中运算放大器选用UA741封装芯片，而乘法器选用具有8引脚的AD633JN封装芯片，通过2个AD633JN乘法器串联来实现状态方程中的立方项.Tina-Ti仿真软件中模拟电路的原理如图14所示，各元器件工作电压为-15～15 V，输入余弦电压信号幅值为25 mV，频率为159 mHz，输出电压测点布置为VF1与VF2，分别与式（19）中的x₁、x₂相对应.

4.2电路仿真与试验结果分析

利用Tina-Ti电路仿真软件中的瞬态响应求解器得到两个测点的电压响应，并与式（19）系统参数分别取ε= 0.05、C= 2、ξ₂= 0.2、f = 0.5、σ=0，初始条件均为0时的数值计算结果进行对比，如图15所示.由图15可知，VF1测点与VF2测点均呈现稳定的强调制响应，这与数值计算结果中位移响应x₁、x₂的变化趋势保持一致，存在的略微差异是由于输入频率只能近似取整为159 mHz，导致相位上存在一定延迟.

依据电路原理图制作电路板，并开展电路试验. 其中信号发生器用于提供外界余弦激励信号，稳压电源设置为±14.9V，用于提供元器件工作电压，示波器用于采集测点VF1和VF2的电压信号，相互连接关系以及电路试验结果分别如图16和图17所示. 由图可知，试验测试结果与电路仿真结果以及Runge-Kutta数值方法结果吻合良好，表明强调制响应检测电路是有效的，也验证了强调制响应在NES系统中是真实存在的.

5结论

利用复变量平均法推导了主共振下NES系统的慢变动力流方程，通过多尺度法研究快变与慢变两个时间尺度上系统平衡点的特性，从慢不变流形相轨迹、慢变流形特征以及松弛振子一维映射等多视角探究了NES系统产生强调制响应的充要条件，通过电路仿真与试验验证了理论分析的正确性.得出如下结论：

到的平衡点.

3）强调制响应检测电路仿真和试验结果与理论分析结果保持一致，验证了NES系统中強调制响应存在的真实性和靶能量传递的可行性.

参考文献

[1] ZHANG Y W，LU Y N，ZHANG W，et al. Nonlinear energy sink with inerter [J]. Mechanical Systems and Signal Processing，2019，125：52-64.

[2]吴长青，张志田，张伟峰.考虑几何非线性的桥梁后颤振极限环特性[J].湖南大学学报（自然科学版），2018，45（5）：1-10.

WU C Q，ZHANG Z T，ZHANG W F. Limit cycle oscillation of bridge post-flutter with geometric nonlinearities [J]. Journal of Hunan University （Natural Sciences），2018，45（5）：1-10. （In Chinese ）

[3]刘良坤，谭平，陈洋洋，等.非线性能量阱减振系统受基底简谐激励的强调制反应分析[J].北京工业大学学报，2019，45（2）：177-185.

LIU L K，TAN P，CHEN Y Y，et al. Strongly modulated response analysis of nonlinear energy sink absorption system under ground harmonic excitation [J]. Journal of Beijing University of Technology，2019，45（2）：177-185.（In Chinese）

[4] XIONG L Y，TANG L H，LIU K F，et al. Broadband piezoelectric vibration energy harvesting using a nonlinear energy sink[J]. Journal of Physics D：Applied Physics，2018，51（18）：185502.

[5] WANG J J，WANG B，WIERSCHEM N E，et al. Dynamic analysis of track nonlinear energy sinks subjected to simple and stochastice excitations [J]. Earthquake Engineering & Structural Dynamics，2020，49（9）：863-883.

[6]JIANG X A，MCFARLAND D M，BERGMAN L A，et al. Steady state passive nonlinear energy pumping in coupled oscillators：theoretical and experimental results[J]. Nonlinear Dynamics，2003，33：87-102.

[7]ZHANG Y W，ZHANG H，HOU S，et al. Vibration suppression of composite laminated plate with nonlinear energy sink[J]. Acta Astronautica，2016，123：109-115.

[8]STAROSVETSKY Y，GENDELMAN O V. Bifurcations of attractors in forced system with nonlinear energy sink：the effect of mass asymmetry[J].Nonlinear Dynamics，2010，59（4）：711-731.

[9]GOURDON E，LAMARQUE C H. Nonlinear energy sink with uncertain parameters[J]. Journal of Computational and Nonlinear Dynamics，2006，1（3）：187-195.

[10]李爽，楼京俊，柴凯，等.激励力幅值对非线性能量阱系统全局分岔特性的影响研究[J].船舶力学，2021，25（4）：479-488.

LI S，LOU J J，CHAI K，et al. Research on the influence of excitation amplitude on global bifurcation characteristics of nonlinear energy sink system[J]. Journal of Ship Mechanics，2021，25（4）：479-488.（In Chinese）

[11]張也弛，孔宪仁，张红亮.非线性耦合振子间的靶能量传递研究：保守系统中的完全能量传递[J].振动与冲击，2012，31 （1）：150-155.

ZHANG Y C，KONG X R，ZHANG H L. Targeted energy transfer among coupled nonlinear oscillators：complete energy exchange in a conservative system[J]. Journal of Vibration and Shock，2012，31（1）：150-155.（In Chinese）

[12] XIE L，BAGUET S，PRABEL B，et al. Bifurcation tracking by Harmonic Balance Method for performance tuning of nonlinear dynamical systems[J].Mechanical Systems and Signal Processing，2017，88：445-461.

[13] CHEN J E，HE W，ZHANG W，et al. Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks[J].Nonlinear Dynamics，2018，91（2）：885-904.