分孔径离轴同时偏振超分辨率成像光学系统像差校正*

孙昇 王超2)† 史浩东 付强 李英超

1)(长春理工大学,空间光电技术国家与地方联合工程研究中心,长春 130022)

2)(中国科学院长春精密光学机械与物理研究所,应用光学国家重点实验室,长春 130033)

针对宽波段同时偏振高分辨率成像需求,提出一种基于反射式自由曲面光学系统和数字微镜器件的分孔径同时偏振超分辨率成像系统,其具有可用于任意光学波段、多个偏振态同时成像、单探测器、高分辨率、易轻量化等优势.给出了这种成像系统光学结构的像差校正原理及设计优化方法,将Wassermann-Wolf 理论进一步发展,推导了可消除多种像差的反射式Wassermann-Wolf 微分方程;同时结合赛德尔像差理论,在求解Wassermann-Wolf 方程时加入消畸变的边界条件,通过迭代方式,得到同时消除球差、彗差、像散、畸变的光学初始结构.对该初始结构进行离轴处理并进一步优化,编写自定义优化评价函数,严格控制各子孔径和各视场在中间像面和最终像面上主光线落点位置,从而有效地抑制最终系统中的畸变,避免超分辨重建过程中的镜元和像元失配误差,提高重建质量.最终完成了四子孔径自由曲面离轴反射式超分辨成像光学系统的设计,其相对孔径大(F#=2.5),结构紧凑,各个偏振通道成像质量接近衍射极限.以上像差校正原理及像质优化方法可有效指导超宽波段同时偏振超分辨率成像光学系统的设计.

1 引言

偏振探测是一种新兴的探测手段,其利用散射光、背景光和目标光的偏振特性差异,具有“穿云透雾,凸显目标,识别真伪”的特殊效果[1].同时偏振成像是一种一次性获取所有偏振态信息的探测方式,可确保每次测量均是在相同的光照和辐射条件下进行,适用于快速变化目标的检测与跟踪,是偏振探测技术的主流体制.可同时偏振成像并满足轻小型化要求的偏振成像系统构型包括分孔径型和分焦平面型两种[2].其中,分焦平面型偏振成像系统结构简单,但会产生瞬时视场失配误差,且难以通过后续图像处理恢复.而采用分孔径型偏振成像系统构型,利用单个焦平面阵列和一个投影系统,可以将同一视场不同偏振方向的图像投影到一个焦平面阵列的不同位置上[3],可采用单探测器同时获取多个偏振方向数据,且无视场失配问题[4].分孔径偏振成像的主要问题是会损失一半空间分辨率,可配合计算超分辨成像方法来提高成像分辨率,增加对物体细节的辨识能力.

分孔径型偏振成像光学系统设计方面,2005年美国Pezzaniti 和Chenault[5]设计了一种中波红外偏振成像探测仪,采用分孔径型偏振成像系统构型,该偏振成像探测仪的核心元件是中继成像透镜,将四幅相同的图像成像到一个单个焦平面探测器上.2007 年美国 Moultrie 等[6]设计了一种微光偏振成像仪,该偏振成像仪基于孔径分割的方法,可在单个电荷耦合器件(CCD)探测器阵列上同时获取四幅子图像.2007 年美国Leon 等[7]设计了一种工作波长为632.8 nm 的分孔径偏振成像仪,相机一次曝光可获取四幅不同的图像,最终的结果以DOP(degree of polarization),DOLP(degree of liner polarization),DOCP(degree of circular polarization)以及椭圆率的形式表示,避免了分振幅成像仪带来的公差要求严格的问题.2014 年苏州大学贺虎成等[8]根据近轴成像特性,分别给出分孔径偏振成像光学系统偏心量与前组、后组焦距的关系,并结合PW法进行系统初始结构的设计.2018 年中国科学院长春精密光学机械与物理研究所王琪等[9]设计了一种分孔径红外偏振成像仪光学系统,采用共孔径与子孔径结合的技术,具有实时性好,结构紧凑的优点.2021 年刘尊辈等[10]设计了分孔径紫外多波段成像光学系统,去除了望远系统,采取前置分孔径系统加后置合像系统的形式,可以提高探测的准确性,减少背景干扰.以上设计均为透射式分孔径偏振成像光学系统,然而,对于材料吸收率较高的红外波段,透射式结构难以满足宽波段红外谱段高能量利用率成像需求,进一步发展反射式分孔径偏振探测光学结构成为红外偏振探测领域的迫切需求.

本文提出了一种分孔径离轴同时偏振超分辨率成像光学系统的设计原理及方法,该光学系统采用了全反射式二次成像结构,宽工作波段,无中心遮拦,能量利用率高,易轻量化.首先简述了自由曲面反射式同时偏振压缩成像系统总体构成和工作原理;之后基于Wassermann-Wolf 理论和赛德尔像差理论,提出该系统初始结构消像差设计原理和整体设计优化方法,最后给出了光学系统设计结果和像质评价,实现了含数字微镜器件(digital micro-mirror device,DMD)的大相对孔径离轴全反射式超分辨率成像光学系统设计.

2 分孔径离轴同时偏振超分辨率成像系统工作原理

利用同时偏振超分辨率成像原理和压缩感知理论,实现宽波段同时偏振超分辨率成像.如图1所示,系统主要组成包括: 分孔径离轴反射式自由曲面光学系统、DMD、红外偏振焦平面探测器、计算超分重建单元等.

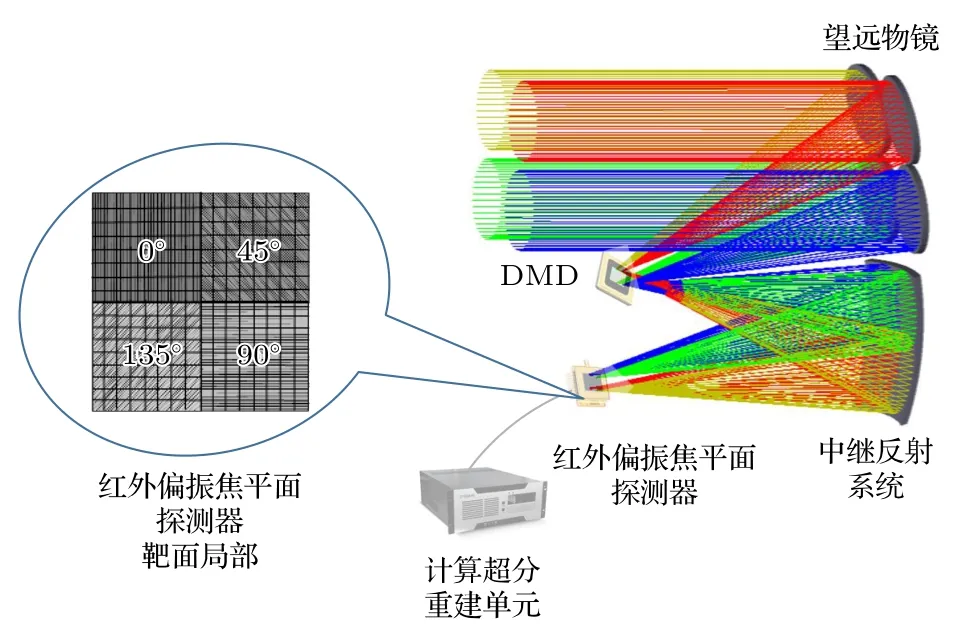
图1 分孔径离轴同时偏振超分辨率成像系统组成图Fig.1.Composition diagram of aperture-divided off-axis simultaneous polarization super-resolution imaging system.

分孔径离轴同时偏振超分辨率成像光学系统由望远物镜和中继反射系统组成.来自远处场景的光线经过望远物镜的四个子入瞳,分别成像到中间像面的四个等大的区域上;利用DMD 对中间像面上的光强进行编码,编码后四束光经DMD 反射,统一经过中继反射系统后分别投影在红外偏振焦平面探测器四个区域上.焦平面“田”字形分割的四个区域分别附加不同方向的宽波段金属光栅偏振片,从而获得四个偏振方向的光强:I(0),I(45),I(90),I(135).变换DMD 编码形式,每变换一次码型进行一次成像,从而获得多帧低分辨率偏振光强灰度图像,经图像处理器进行亚像元重建后输出各个偏振方向的超分辨率偏振图像,进而计算出目标的Stokes 参数[11-15].

3 分孔径离轴同时偏振超分辨率成像光学系统像差校正原理与方法

3.1 基于Wassermann-Wolf 理论和赛德尔系数的光学系统消像差原理

该光学系统采用全反射式结构,属于二次成像系统.一次成像部分为望远物镜,二次成像部分为中继反射系统,中间像面与DMD 相重合.其中像差校正的重点和难点在二次成像部分,其需要满足两个条件: 一是消除球差、彗差、像散等各类影响像质的波像差项;二是为了将n×n(n为超分辨倍率)的编码码元精确投影到探测器的1 个像元上,需严格消除畸变这一不影响像质的像差项.

由于中继反射光学系统缺乏现成的专利数据作为设计起点,将经典的Wassermann-Wolf(WW)[16]设计理论进一步发展,运用至该系统的光学初始结构设计.推导适用于中继反射系统的WW 方程,求解一对消球差、彗差、像散的W-W 表面.

一对同轴反射式W-W 表面M1,M2如图2 所示.光线从左边入射,依次经过M1和M2两个反射面,最终到达像面.其中,i0为M1的入射光线,i1为M2的入射光线,i2为M2的出射光线;设光线与曲面交点为(y,z),将直角坐标写成参数方程的形式为:y=y(t),z=z(t).设i0在M1上的落点坐标为(y1,z1),i1在M2上的落点坐标为(y2,z2),ω*为反射镜M1的光线孔径角,ω＇为反射镜M2的光线孔径角,h1为入射光线i0延长线与M1顶点切线交点A的纵坐标,h2为入射光线i1延长线与M2顶点切线交点B的纵坐标.d1为物面到反射镜M1的距离,d2为两反射镜间距,d3为反射镜M2到像面的距离[17].

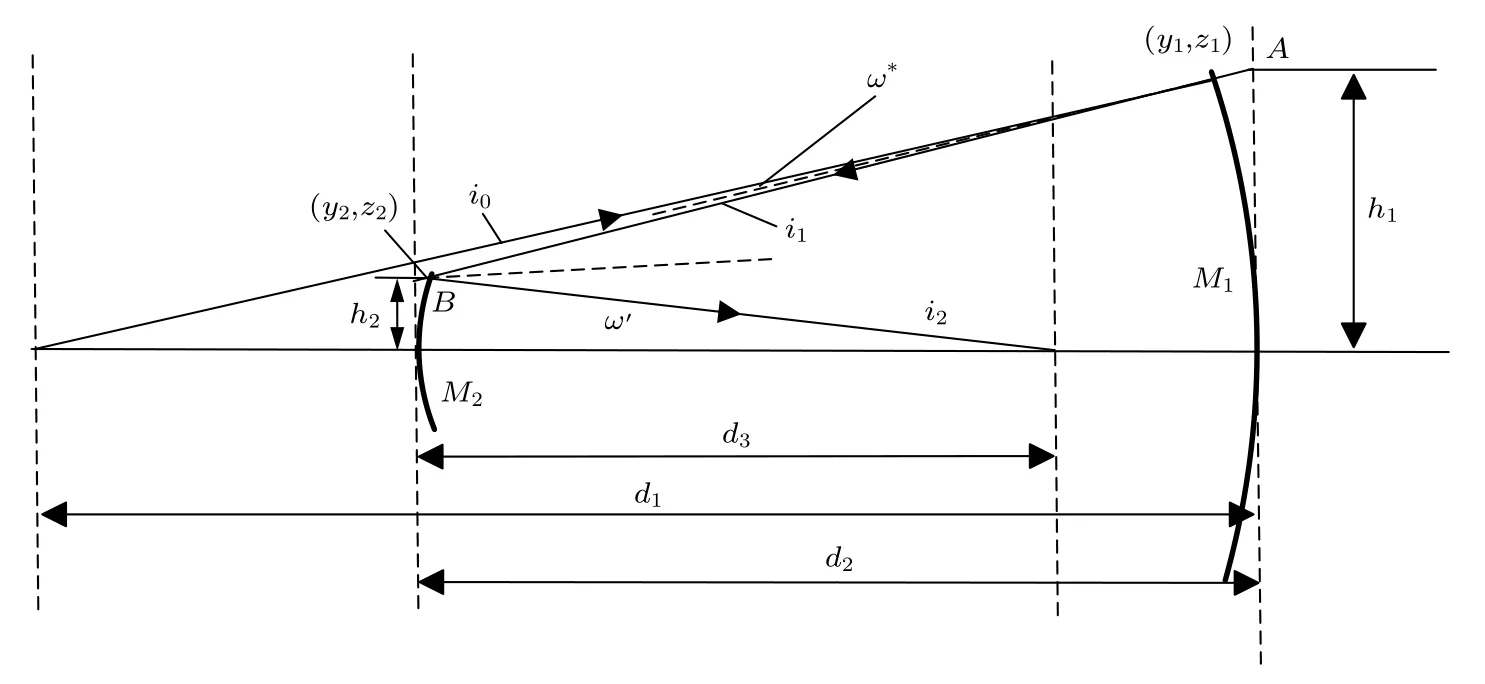
图2 同轴两反W-W 模型Fig.2.W-W model of coaxial two-mirror system.

结合正弦条件与反射定律,得出一组同轴两反的W-W 微分方程:

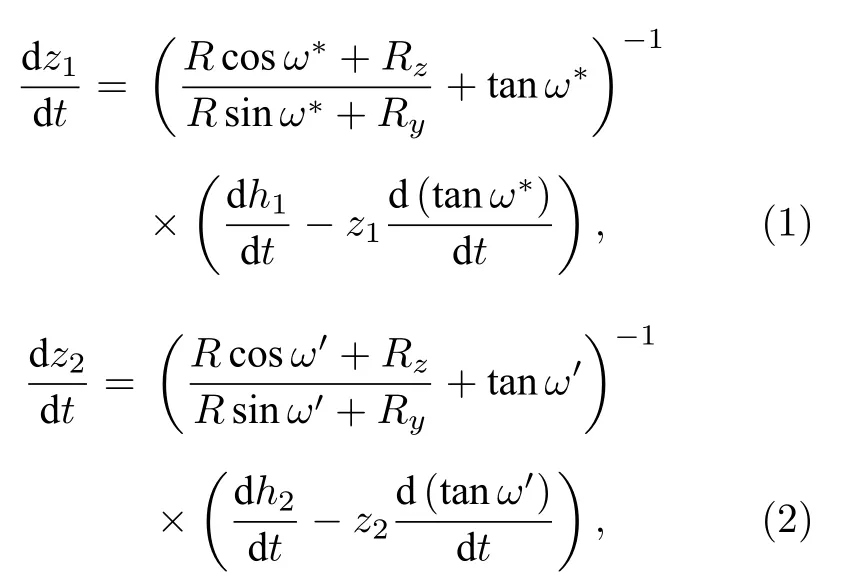
其中Rz=d2+z2-z1,Ry=y2-y1,R=,y1=h1-z1tanω*,y2=h2-z2tanω＇.

求解(1)式和(2)式的过程中,还需满足正弦条件:

其中ω*为入射光线的孔径角,ω＇为出射光线的孔径角,C为常数.

在W-W 两反射面求解过程中,为了使系统结构紧凑,并有合适的伸出量,给出合适的d1,d2和d3的值作为求解的初始条件.其中,d1决定中继反射系统的总体长度,根据系统尺寸要求确定其初值,d2和d3初始值与d1相同.确定后,从主光线开始在物空间追迹光线到M1的切平面,将ω*和h1值储存起来.在像空间,追迹从像点出发的主光线到M2的切平面,将ω＇和h2值储存起来.进而计算.设初始值为y1=0,z1=0 和y2=0,z2=0.利用Runge-Kutta 算法求解下一组z1和z2,即两个表面上的光线交点的z坐标,随之求出y1,y2.记录下(y1,z1),(y2,z2),用作下一次迭代的初值.重复以上过程多次,直到所有光线都计算完成.

解出一系列满足微分方程的坐标,选择偶次非球面面形,对得到的离散数据点进行拟合.最终M1,M2的表面矢高s1,s2分别满足如下方程:

式中,r1,r2分别为反射镜M1和反射镜M2的曲率半径;e1,e2分别为反射镜M1和M2的曲面二次系数;γ为垂直光轴方向的径向坐标;aiγ2i为非球面的高次项.

接下来推导消畸变方程.根据赛德尔像差理论,初级畸变的PW 形式表达式为[18]

式中y为主光线在反射镜上的高度;J为光学系统的阿贝常数;h为边缘视场光线在反射镜上的高度;φ为光学元件的光焦度;P,W,K的表达式分别为

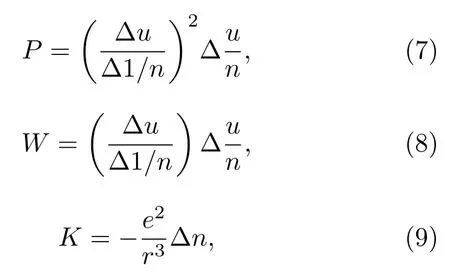
其中 Δn为物方、像方介质的折射率之差,Δu为光学系统的物方、像方孔径角之差,r为反射镜曲率半径,e为反射镜曲面二次系数.

令α为反射镜M2对M1的遮拦比,β2为反射镜M2的放大倍率,β为整个中继反射系统的放大倍率.将反射镜曲率半径、PW 法的P,W,K参量等用α和β2表示,并代入(6)式可得

式中α=h2/h1;h1,h2分别为边缘视场光线在两个反射镜上的高度;β=l2/l1,其中l1,l2分别为DMD 和红外偏振焦平面探测器靶面的边长尺寸.放大倍率β由DMD 的反射面大小和探测器的靶面大小决定,是一个已知量.

中继反射系统初始结构的完整求解流程如图3.将前文进行第一次W-W 方程求解并拟合后得出的两个非球面的e1,r1,e2,r2以及di(i=1,2,3)代入(10)式,如得到的S5值较大,则采用基于模拟退火的多变量函数优化法[19]寻找更合理的系统参数值.进行多轮循环,每次循环中随机性的给d1,d2,d3其中一个参数添加扰动量,其他参数保持不变.di均在一定范围内波动,d1,d2∈[100,150],d3∈[50,100],d2＜d1,单位为mm.基于新的di重新求解W-W 方程得到新的S5,如S5变小则接受新的di,反之则根据Metropolis 准则决定是否接受di.如此循环直到温度降低到设定的终止温度.此时可认为完成了消球差、彗差、像散、畸变的中继反射系统的初始结构设计.

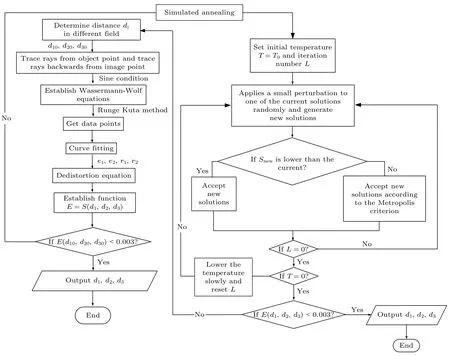
图3 中继反射系统初始结构求解流程图Fig.3.Initial structure design flow chart of relay reflection optical system.

3.2 分孔径离轴同时偏振超分辨率成像光学系统设计方法

3.2.1 望远物镜设计

以单孔径同轴旋转对称式光路作为设计起点,给单片反射镜增加子午方向的离轴、倾斜量,将一次像面调整至合适的位置,确定望远物镜整体结构;接下来复杂化反射镜面形,逐步增加面形数理模型的自由度(偶次非球面→X-Y多项式自由曲面),直到单孔径望远物镜像质接近衍射极限;接下来对望远物镜进行分裂孔径设计,对望远物镜入瞳分别进行X方向和Y方向适当偏心,共4 次,获得含4 个子孔径的光路,且为了缩小整体体积,各孔径需紧密靠在一起,综上获得了分孔径望远物镜的光学初始结构.

由于同时偏振成像需求,要求望远物镜的4 个子孔径分别成像在一次像面处的DMD 等大的四个区域上;四幅图像排列紧密,图像之间不能存在缝隙,从而最大化利用DMD 镜元.因此在优化中,需要对各子孔径系统主光线在DMD 处的落点加以控制.

如图4 所示,在每一个子孔径的像面区域取3×3 典型视场采样点,黑色的点为理想的各视场主光线落点位置,灰色的点为实际光线落点,由于系统关于yoz平面对称,只需要提取子孔径1 和子孔径3 的5×3 个视场采样点进行计算.

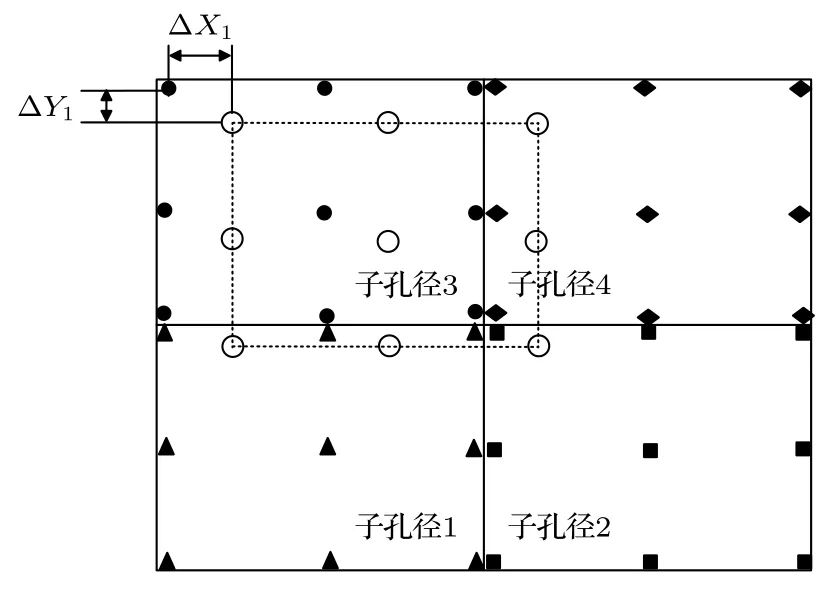
图4 像面处光线理想落点Fig.4.Ideal light spot at the image plane.

利用ZEMAX 宏语言编写自定义优化评价函数,使用RAGX 和RAGY 操作数追迹光线在DMD 上的落点坐标,并获取实际光线落点与理想落点的均方根距离差,编写自定义评价函数,其表达式为

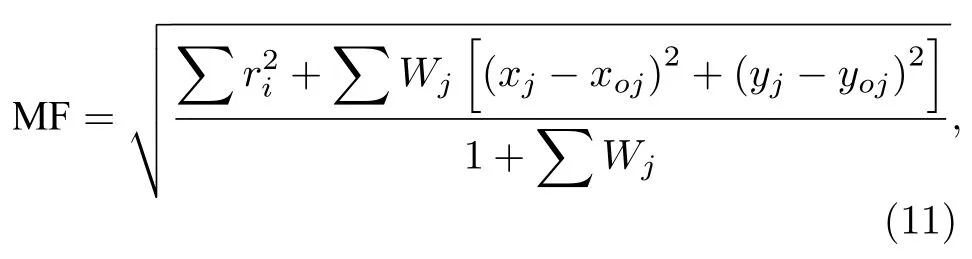
式中,ri为不同视场下弥散斑半径;Wj为不同视场采样点的优化权重值;xi,yi为每个视场的主光线实际落点的坐标值,xoj,yoj为不同视场采样点的理想坐标值,其中,i代表视场的标号,取值范围为1-15.优化时,在自定义评价函数的基础上加入子午和弧矢面的调制传递函数(modulation transfer function,MTF)值及垂轴像差值作为评价,进行优化直到评价函数达到极小值,即完成了望远物镜的设计.

3.2.2 中继反射系统及整体光学系统设计

基于3.1 节中的同轴系统消像差原理,列出同轴中继反射系统的W-W 微分方程并求解,获得一对同轴消像差反射面.为了避免中心遮拦,获得良好的成像质量,对中继反射系统初始结构进行离轴处理.适当复杂化反射镜面形,并使用DISG,DIMX等操作数控制畸变,直到中继反射系统像质接近衍射极限.

最后将望远物镜与中继反射系统相连接,前者的像面作为后者的物面.将一次像面的表面面形由平面换为DMD 微镜阵列面形.望远物镜参数保持不变,仅放开中继反射系统的表面面形参数与两个表面的偏心量、倾斜量等作为优化变量.接下来仿照(11)式编写优化评价函数,使各子孔径在最终像面上的光线落点尽量接近理想值,并控制整体光学系统像质,从而完成了光学系统整体的设计.

4 分孔径离轴同时偏振超分辨率成像光学系统设计

4.1 设计结果

基于前文所述设计原理及方法,设计了分孔径离轴超分辨率成像光学系统.其主要技术指标如表1 所列.

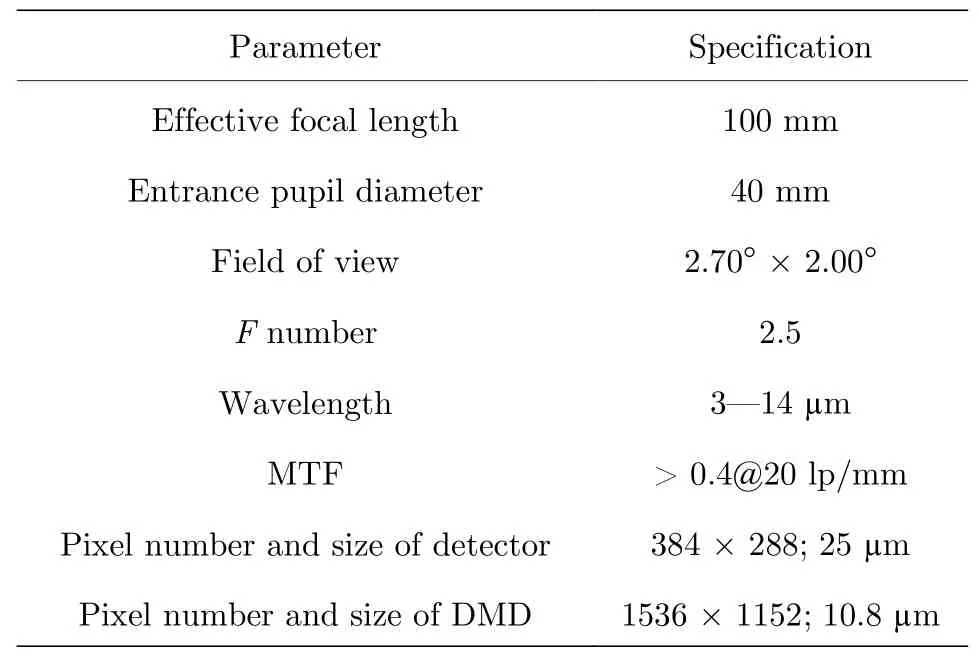
表1 分孔径离轴同时偏振超分辨率成像光学系统指标Table 1. Specification of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system.

该成像光学系统使用的探测器为在北方广微公司GWIR 0202X1A 非制冷型中长波红外探测器基础上开发的偏振红外探测器,在红外焦平面附着不同方向的金属光栅偏振片,靶面偏振方向分布如图1 所示.分孔径离轴同时偏振超分辨率成像光学系统的三维光路见图5.系统焦距为100 mm,视场由探测器靶面大小决定,横向长度为150 mm,纵向长度为147.33 mm,结构较为紧凑.4 个子孔径反射镜、次镜、三镜均为X-Y多项式面形,其中次镜、三镜组成中继反射系统.首先如3.2.1 节中所述完成望远物镜设计,之后按照3.1 节中的方法求解W-W 微分方程,得到次镜、三镜的面形数据点,如表2 所列,其中N为面形数据点序号.此时d1=150 mm,d2=-144.122 mm,d3=94.67 mm.通过拟合程序将次镜和三镜的数据用3.1 节中的方法进行拟合,将拟合得到的一对W-W 曲面导入到 ZEMAX 光学设计软件中,搭建中继反射系统初始结构,并对次镜和三镜进行离轴优化以避免光线遮拦.将望远物镜和中继反射系统进行连接,在一次像面处引入DMD 表面,DMD 表面有多个微镜,具有开、关两种状态.开状态时,DMD 上的反射光线正常进入中继反射系统;关状态时,DMD出射光线全部反射到镜筒内壁,如图6.此时可以通过镜筒内壁涂黑来对非正常光路中的光线进行吸收,避免杂光进入探测器.将各个子孔径的视场扩大到覆盖整个DMD 区域,在光学设计软件中通过不超过10 次的迭代优化得到最终结果.各镜片参数如表3.

图5 分孔径离轴同时偏振超分辨率成像光学系统光路图Fig.5.Layout of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system.

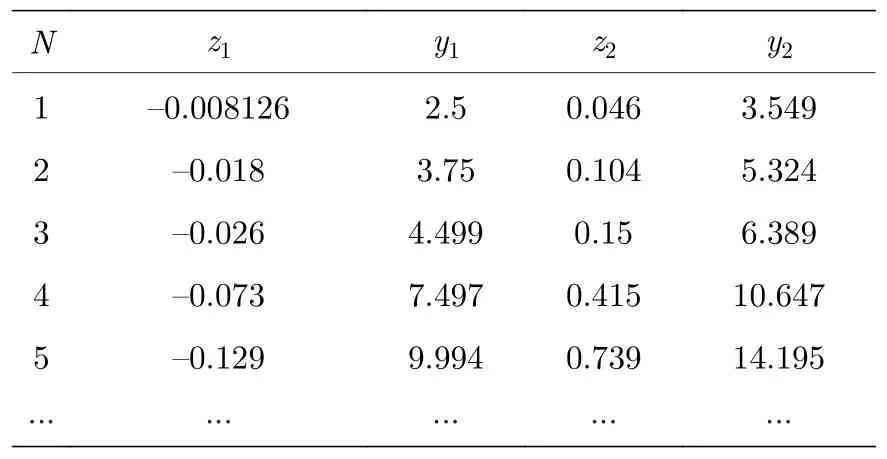
表2 次镜和三镜的面形数据点Table 2. Profile data points of M1 and M2.

图6 DMD 微镜处于关状态时光线走向示意Fig.6.Direction of the light when the DMD micro-mirror is off.

表3 镜头参数Table 3. Lens parameters.

利用MTF 曲线、弥散斑半径、光线像差曲线、光迹分布等对望远物镜、中继反射系统以及整体光学系统的设计结果进行评价,结果如图7-图13所示.图7 为望远物镜各个子孔径的MTF 曲线图,图8 为中继反射系统的光路图、MTF 曲线、点列图以及网格畸变,可见两部分子系统的像差都得到了很好的校正,可保证后续压缩感知图像重建效果.图9 为光学系统整体MTF 图,各个子孔径在系统截止频率20 lp/mm 处的MTF 值均大于0.4;图10 为DMD 处与红外偏振焦平面探测器上光线落点图,可见4 个子孔径在各个不同视场的成像基本处于理想位置,各视场中心光线偏离理想落点最大不超过1 个像元,保证超分辨率编码重建效果.图11 为各子孔径的点列图,可见光学系统各个子孔径光斑均方根(root mean square,RMS)半径均小于探测器像元尺寸;图12 为各子孔径的光线像差曲线图,可见各子孔径初级像差基本被消除,成像质量良好.图13 为各个子孔径的网格畸变图,可见全视场畸变值均小于0.5%.

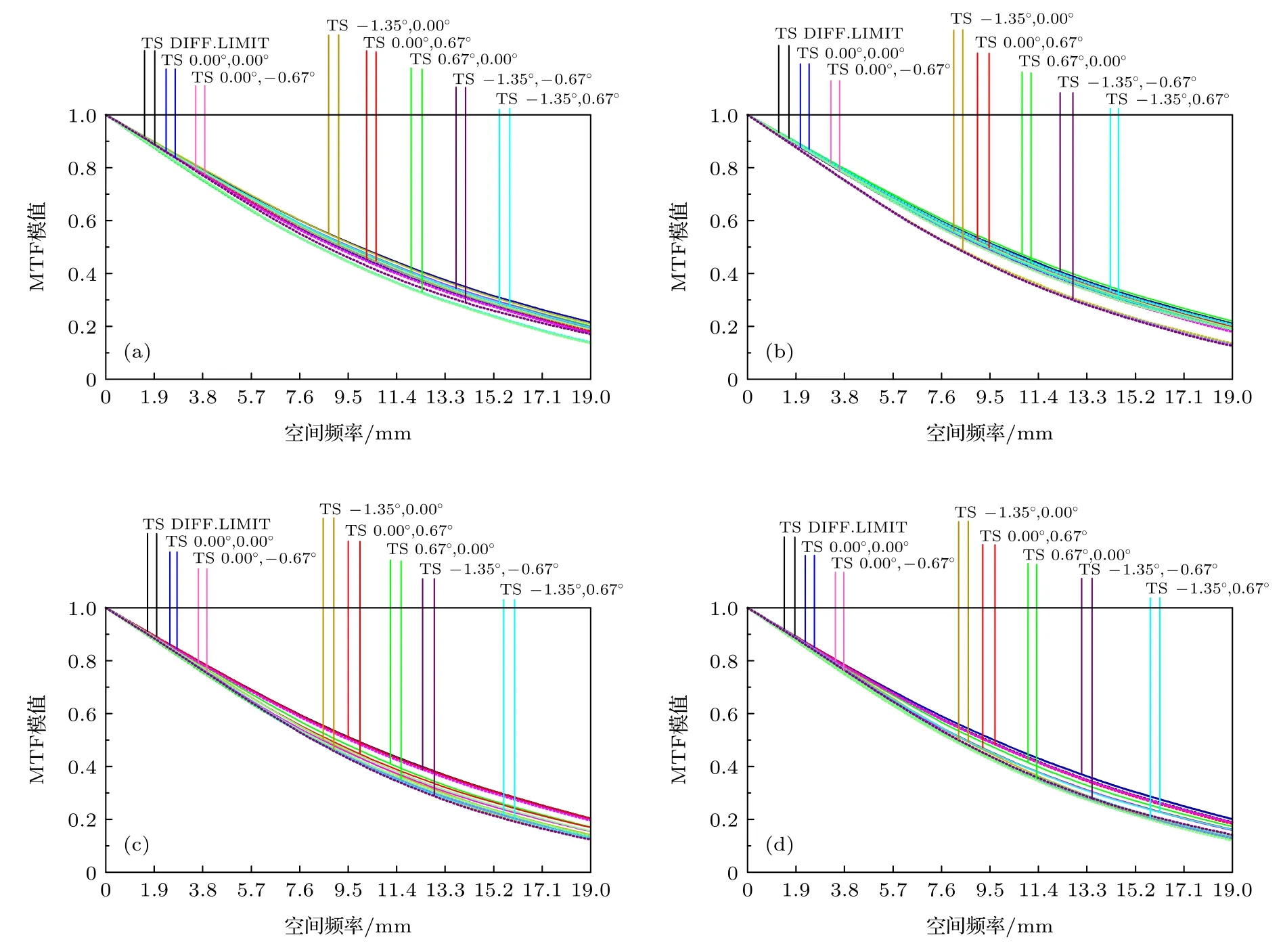
图7 望远物镜MTF 曲线图(T 代表子午方向,S 代表弧矢方向)(a)子孔径1;(b)子孔径2;(c)子孔径3;(d)子孔径4Fig.7.MTF of Long-range objective:(a)Sub-aperture 1;(b)sub-aperture 2;(c)sub-aperture 3;(d)sub-aperture 4.

图8 中继反射系统像质评价(a)光路图;(b)MTF;(c)点列图;(d)网格畸变Fig.8.Image quality evaluation of relay reflection optical system:(a)Layout;(b)MTF;(c)spot diagram;(d)grid distortion.

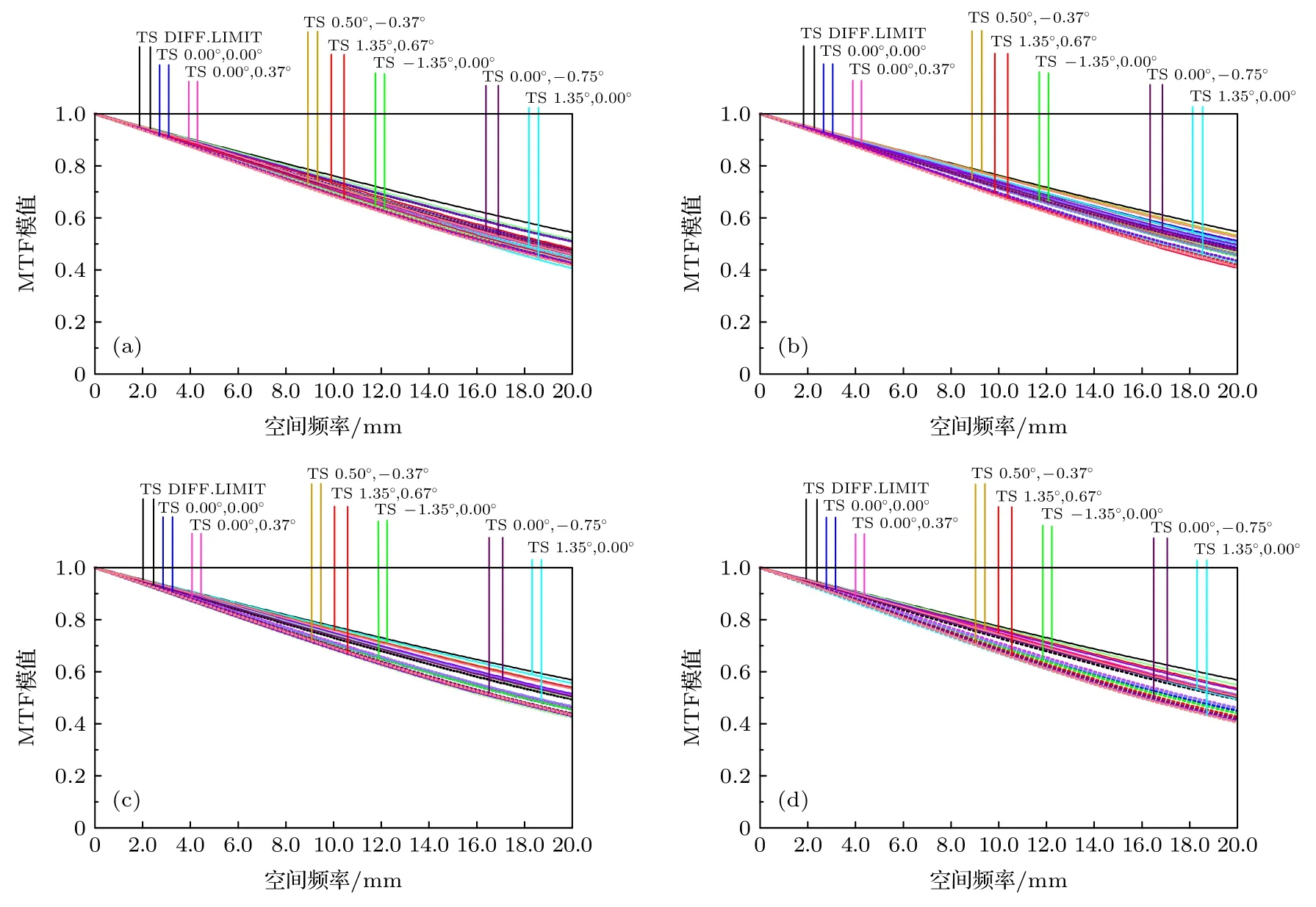
图9 分孔径离轴同时偏振超分辨率成像光学系统调制传递函数(a)子孔径1;(b)子孔径2;(c)子孔径3;(d)子孔径4Fig.9.MTF of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system:(a)Sub-aperture 1;(b)sub-aperture 2;(c)sub-aperture 3;(d)sub-aperture 4.

图10 分孔径离轴同时偏振超分辨率成像光学系统光迹分布图(a)DMD 处;(b)像面处Fig.10.Footprint diagram of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system:(a)At the DMD plane;(b)at the image plane.

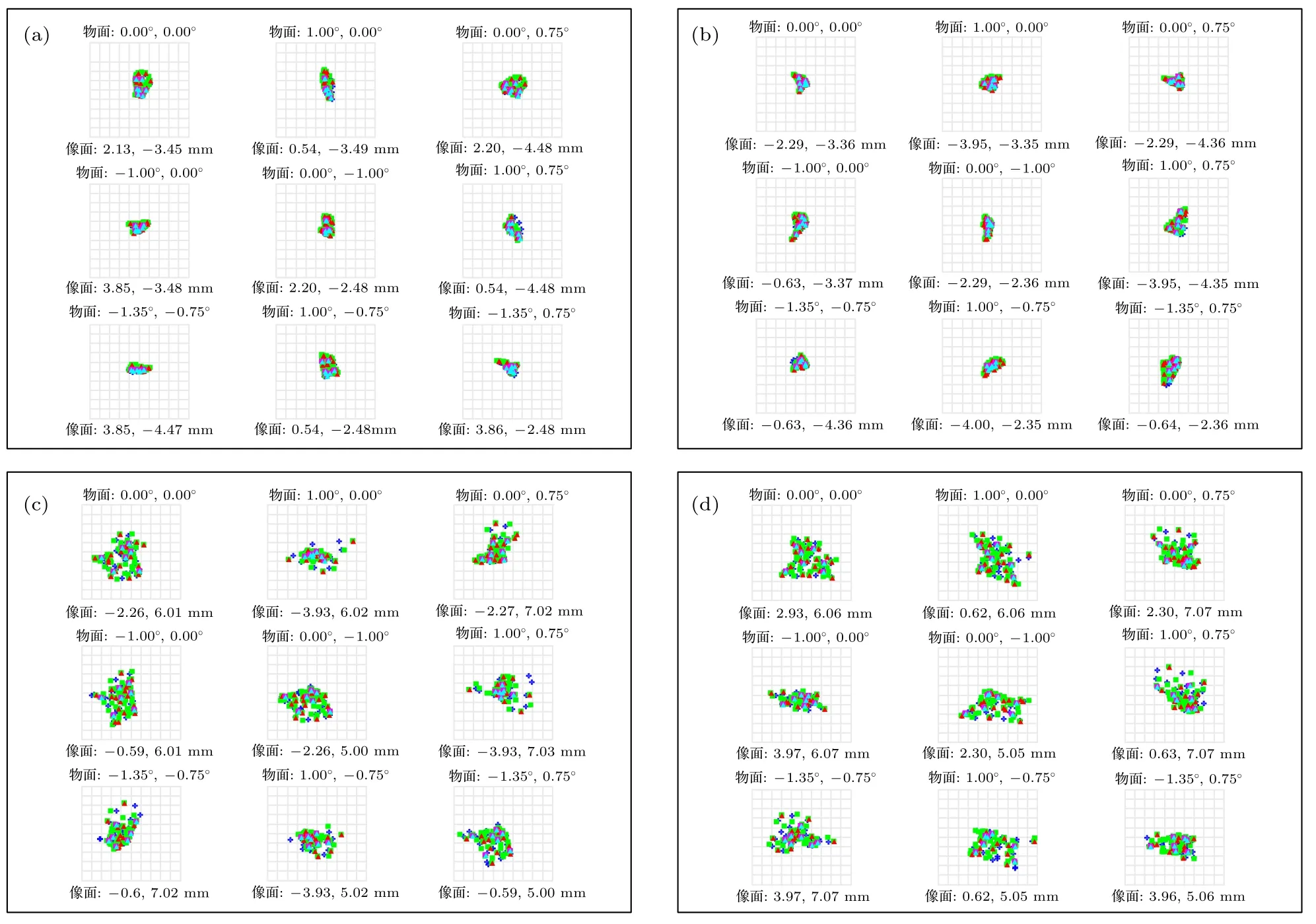
图11 分孔径离轴同时偏振超分辨率成像光学系统点列图(a)子孔径1;(b)子孔径2;(c)子孔径3;(d)子孔径4Fig.11.Spot diagram of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system:(a)Sub-aperture 1;(b)sub-aperture 2;(c)sub-aperture 3;(d)sub-aperture 4.

图12 分孔径离轴同时偏振超分辨率成像光学系统光线像差曲线图(a)子孔径1;(b)子孔径2;(c)子孔径3;(d)子孔径4Fig.12.Ray aberration of aperture-divided off-axis simultaneous polarization super-resolution imaging optical system:(a)Sub-aperture 1;(b)sub-aperture 2;(c)sub-aperture 3;(d)sub-aperture 4.

图13 全系统网格畸变(a)子孔径1;(b)子孔径2;(c)子孔径3;(d)子孔径4Fig.13.Grid Distortion:(a)Sub-aperture 1;(b)sub-aperture 2;(c)sub-aperture 3;(d)sub-aperture 4.

4.2 公差分析

光学系统的公差分为装调公差和加工公差,该反射式系统的装调公差包括: 沿xyz轴的平移公差、绕xyz轴的倾斜公差.加工公差包括: 曲率半径公差、二次曲面系数公差、自由曲面面型公差,公差分配如表4 所列.国内制造能力可以满足本系统的加工装调精度需求[18,20-23].

使用系统RMS 波像差作为最终评价标准,对系统进行500 次蒙特卡罗公差分析,公差参数分配如表4 所示.根据蒙特卡罗分析得知,98%的样本RMS 波像差小于0.08λ(λ=8 μm),满足清晰成像要求.

表4 光学系统的公差分配Table 4. Tolerance distribution of optical system.

5 结论

提出一种利用分孔径反射式自由曲面光学系统和DMD 编码器件实现的分孔径离轴同时偏振超分辨率成像系统,其具有可用于任意光学波段、多个偏振态同时成像、单探测器、高分辨率、易轻量化等优势.同时,研究并获得了含有DMD 的自由曲面离轴反射式分孔径光学系统设计原理及方法.将《光学原理》中经典的W-W 理论进一步发展,推导了适用于反射式系统,可消除多种像差的反射式W-W 微分方程;同时结合赛德尔像差理论,在求解W-W 方程时通过迭代的方式令求出的解满足消畸变的边界条件,从而得到同时消除球差、彗差、像散、畸变的光学初始结构.同时,建立严格控制各子孔径各视场在中间像面和最终像面上主光线落点位置的像质优化评价函数,从而在光学层面上有效地抑制了超分辨重建过程中的失配误差.最终完成了4 子孔径自由曲面离轴反射式超分辨成像光学系统的设计,其各个反射镜面形均为X-Y多项式自由曲面,相对孔径大(F#=2.5),结构紧凑,一次像面DMD 处与最终像面处,各子孔径、各视场像质均接近衍射极限,可满足各个偏振通道成像质量良好的要求.该设计原理及方法可填补宽波段同时偏振超分辨率成像光学系统设计理论的空白,解决传统设计方法用于此特殊系统时,设计效率低,设计结果可靠性差的问题.这种特殊光学系统要投入实际制造,公差分析是必要的一步,因此,下一步计划结合目前我国自由曲面加工水平,为自由曲面曲率半径、多项式系数、反射镜间隔、偏心以及绕x轴倾斜量分配公差值,建立该光学系统的公差模型,为完成实际系统做准备.