线性和非线性干涉仪中宇称测量的特性研究
张建东,王 帅
(江苏理工学院 数理学院,江苏 常州 213001)
0 引言
光学干涉仪具有亚波长量级的测量能力,在微弱信号检测方面展现出重要的应用价值。传统的干涉仪使用相干态作为输入,其测量精度受限于散粒噪声极限为干涉仪中的平均光子数)。为进一步提升测量精度,需要使用量子态作为输入。近年来,许多测量精度能够突破散粒噪声极限的方案陆续被报道,基于N00N态、双模压缩真空态和纠缠相干态等量子态输入的测量精度甚至能够实现海森堡极限。除了量子态本身的奇异特性,基于光子数分辨的测量策略也是测量精度提升的关键。
作为一类常见的光子数分辨策略,宇称测量在量子精密测量方面具有至关重要的作用,其测量算符的形式为Π=exp(iπn)[4-6]。宇称测量最早由Bollinger等人在研究原子态探测时提出[7],随后被Gerry等人应用于相位估计方面[8,9]。对于光学干涉仪,宇称测量仅探测并分辨两个输出端中任意一端的光子数。当探测到的光子数为奇(偶)数时,测量结果被记为-1(1)。因此,测量信号可以表示为偶数光子概率与奇数光子概率的差值,即。
理论上,宇称测量的实现仅需要单一的光子数分辨探测器。但是目前大光子数的光子分辨仍然是一个难题。为了解决这一问题,Plick等人提出了一种替代的方法,他们使用平衡零差测量重构输出态的Wigner函数,进而间接实现宇称测量[10]。另一方面,宇称测量的理论研究也获得了大量关注。先前的研究已经建立了基于相空间的计算方法,可以获得测量信号的解析表示[11]。但是这一方法仅适用于高斯态输入的情况[12,13]。最近,基于有序积分算符技术,我们发展了一种可以用于非高斯态测量信号的解析计算方法[14]。
目前为止,宇称测量被广泛应用于线性和非线性干涉仪中,并且被证明是许多测量方案的最佳策略[15]。但是对不同输出端口实施宇称测量是否等价尚未被讨论。本文针对这一问题开展研究,分别分析了线性和非线性干涉仪中宇称测量信号的特点。在此基础上,还讨论了测量信号与测量精度之间的关系,并对研究结果的物理机制进行了分析。
1 线性干涉仪的宇称测量信号
线性干涉仪也被称为SU(2)干涉仪[16-18],其结构如图1(a)所示。在线性干涉仪中,输入态通过线性分束器进行分束和合束。一般情况下,这类干涉仪被用来估计两个干涉臂之间的相位差。根据SU(2)群理论和算符等式

图1 线性干涉仪和非线性干涉仪示意图

整个干涉仪可以被表示为

式中UBS=exp(-iπJ1/2)和UPS=exp(-iθJ3)分别是分束器和相位移动的算符化表示,

为角动量分量算符。对于双模干涉仪(线性和非线性干涉仪),所有涉及的光学操作均可以通过算符J1、J2和J3进行表示。物理上,这些操作对应于绕着角动量空间中三个轴的旋转操作[19]。数学上,这些操作对应的算符是SU(2)群的转动元。因此,光学操作算符被称为转动算符或转动元,式(3)中的算符被称为转动生成算符或转动生成元。

再根据式(1),可以得到如下关系式
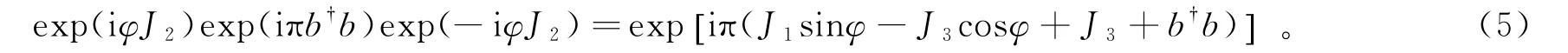
当φ=π时,式(5)转化为
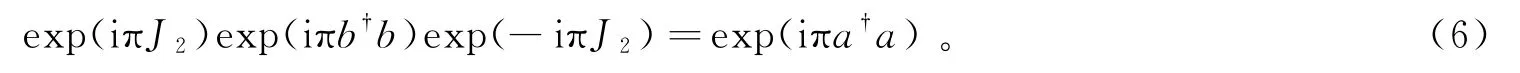
因此,我们得到

式(7)表明,对于线性干涉仪的两个输出端口实施宇称测量是等价的。当待测相位的平移量为π时,两个输出端口的测量信号可以完全重合。
为了检验上述结论,图2展示了两个典型方案的测量信号[2,20]。对于相干态输入的情况,图2(a)说明B端口的测量信号平移π后可以与A端口的测量信号重合。对于双模压缩态输入的情况,图2(b)同样验证了式(7)的结论。需要注意的是,双模压缩真空态的方案具有2重分辨特性,即信号中极大值的数量为相干态方案的两倍。因此,平移量为π时,B端口的测量信号与A端口的测量信号和自身均重合。

图2 线性干涉仪的宇称测量信号(=100)
2 非线性干涉仪的宇称测量信号
非线性干涉仪也被称为SU(1,1)干涉仪[21,22],其合束与分束由非线性过程(如:四波混频)实现,结构如图1(b)所示。由于分束和合束过程的非线性增益,干涉仪内的总光子数会发生变化。因此,通常将第一个非线性分束器后的光子数定义为总光子数[23-25]。此外,不同于线性干涉仪,非线性干涉仪通常被用来测量干涉臂相对于泵浦光的相位和。
首先考虑SU(1,1)群中的3个转动生成算符
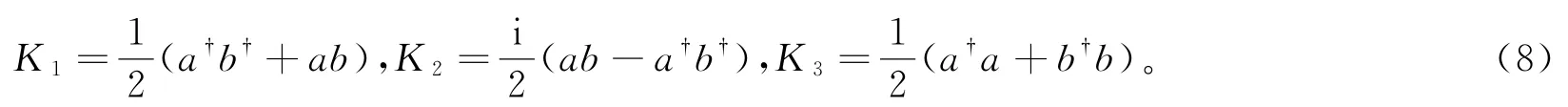

考虑相位移动算符U′PS=exp[i(θ+φ)K3],则B端口的测量信号可以表示为

如果两个端口的宇称测量是等价的,则必然存在一个常量φ使得恒成立。
基于式(1),式(9)和式(10)中的算符可以改写为
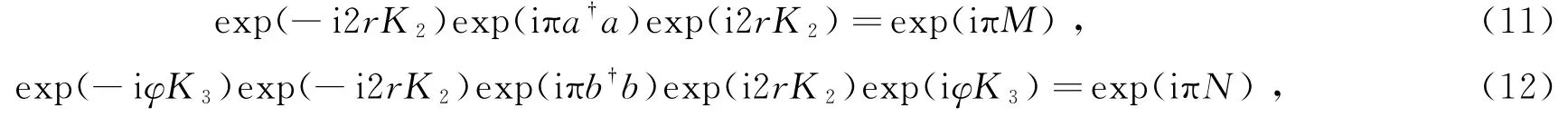
式中

为了检验这一结论,我们同样分析了两个典型方案的测量信号[26],如图3所示。图3(a)的输入态为相干态和热态,图3(b)的输入态为压缩真空态和热态。图中结果表明,两个端口的测量信号不同,并且无法通过平移操作实现重合。这些结果均说明:在非线性干涉仪中,对两个输出端口实施宇称测量并不等价。

图3 非线性干涉仪的宇称测量信号
3 原因分析与进一步讨论
上述章节展示了线性和非线性干涉仪中的宇称测量信号。这里首先讨论两种干涉仪之间的区别。值得注意的是,线性干涉仪中的分束器是无源且平衡的。因此,干涉仪内的总光子数是守恒的。即使两个端口的入射态是任意的,两个干涉臂的平均光子数是相同的。这是因为分束器对于两个模式的算符变换关系可以表示为

当输入态经过第一个分束器后,两个干涉臂的平均光子数差为

这一特性使得两个端口的测量信号可以通过平移操作而相互重合。
但是对于非线性干涉仪,两个非线性分束器是有源且非平衡的,它对于两个模式的算符变换关系为

式中g为非线性分束器的增益系数。
经过第一个非线性分束器后,两干涉臂的平均光子数差一般不为0。即两个干涉臂的平均光子数通常不相同。由于光子数分布的不对称性,两个端口的测量信号不能通过平移操作而重合。特别地,当两个端口输入态相同时,两个干涉臂的平均光子数差为0。此时可以在两个干涉臂中获得对称的光子数分布,两个端口的测量信号能够重合且无需平移。
在此基础上,我们对比分析宇称测量与常规强度测量的特性。根据经典Fisher信息,宇称测量的测量精度可以由误差传递公式计算得到

式中θ是待测相位,与最优测量精度对应的相位值称为最佳工作点θ0。
如图2和图3所示,相比于强度测量,宇称测量的测量信号具有更加明显的尖峰,并且测量信号最大值对应的相位值恰是最佳工作点。这导致宇称测量的测量信号具有更窄的半高全宽。一般而言,经典干涉测量(相干态输入和强度测量)的信号半高全宽被称为衍射极限[27]。当某一方案的分辨率窄于衍射极限时,则被称为超分辨。容易验证,宇称测量的信号具有超分辨特性,这种特性在实际应用中可以缩短扫描区间,具有很大的优势。
另外,式(20)中的分母随着分辨率的增加而增大,这意味着宇称测量通常具有优于常规强度测量的测量精度。另一方面,超分辨率也导致了其他问题。如上所述,最佳工作点附近的测量信号具有较大的斜率,确保了测量精度的提高。然而,当待测相位偏离最佳工作点时,测量信号的斜率迅速减小,这表明测量精度也将迅速下降。综上所述,与强度测量相比,宇称测量通常具有更高的测量精度,但高精度的测量范围较小。
为了更直观地理解这一结论,我们以相干态输入的线性干涉仪为例。图4绘制了不同平均光子数情况下的测量信号与相应的测量精度。从图4(a)中可以发现,测量方案的信号分辨率随着平均光子数的增加而提高。因此,对于最佳工作点,高光子方案在测量精度上优于低光子方案。然而,当待测相位偏离最佳工作点时,高光子方案的测量精度迅速下降。如图4(b)所示,当θ=0.5时,高光子方案的测量精度甚至不如低光子方案。类似的结果在使用其他输入态的测量方案中也广泛存在。若要将宇称测量用于高光子方案,可以通过相位补偿或者自适应算法使得待测相位处于最佳工作点附近。

图4 基于相干态输入的线性干涉仪性能
在实际测量系统中,由于光学器件和周围环境的反射和吸收,不可避免地会产生光子损耗现象。对于常规的强度测量,最佳工作点不随损耗率而变化。然而,宇称测量的最佳工作点将在损耗环境中发生偏移。
图5(a)展示了基于双模压缩真空态输入的线性干涉仪的测量精度。在无损耗情况下,最佳工作点位于π/2,而在损耗环境下,最佳工作点将偏离π/2。图5(b)给出了偏移量与平均光子数和损耗比的关系,其中θ0-π/2被定义为偏移量。结果表明,偏移量随损耗率的增加或者光子数的减少而增大。

图5 基于双模压缩真空态输入的线性干涉仪性能(=100)
值得注意的是,在基于相干态的测量方案中,最佳工作点不会发生偏移。产生这种差异的物理原因是光子损耗破坏了量子态的相干性,但是相干态的相干性在光子损耗的情况下保持不变。鉴于宇称测量的这一特性,在实际测量中,需要评估平均光子数和损耗率以确定最佳工作点。
4 结论
本文研究了线性和非线性干涉仪中的宇称测量信号特性,重点分析了两个输出端口的测量信号之间的等效性。结果表明,任意输入态的情况下,对线性干涉仪两个端口实施宇称测量均等价。然而,只有两个端口的输入态相同的情况下,对非线性干涉仪两个端口实施宇称测量是等价的。此外,我们还通过对一些测量方案的讨论,分析了导致这些结果的原因并探明了线性和非线性干涉仪之间的差异。最后,我们总结了宇称测量在分辨率和测量精度方面的特性。研究结果为基于宇称测量的实用化量子精密测量方案设计提供了理论指导。

