基于敏感因子指数法的垃圾填埋场地下水污染过程识别技术中权重计算方法优化

黄彦，张洁，杨周白露

（1.江西核工业环境保护中心，江西 南昌 330002；2.江西省水利科学院，江西 南昌 330029；3.江西水利职业学院，江西 南昌 330006）

0 引言

垃圾填埋场目前已成为地下水主要污染源之一，而填埋场对地下水的污染，归根结底是垃圾渗滤液透过土壤对地下水的污染［1,2］。垃圾渗滤液中含有高浓度的溶解性有机物和还原性无机物［3］，如果渗漏进入地下水中，其中的部分还原性污染物会和地层中的各种氧化性物质发生氧化还原作用，由于不同的氧化还原反应所需的能量不一，因而造成了在不同的氧化还原环境中发生不同的氧化还原反应的难易程度和次序的不同，这样就导致在地下水流方向上形成了一系列的氧化还原特征区［4-7］。这些氧化还原特征区对污染物的衰减起到重要的作用，控制地下水环境中有机物的降解和无机化学反应的进行。因此，了解氧化还原作用的分布规律是模拟预测污染物在地下环境中衰减和迁移转化的前提，可为垃圾填埋场污染地下水的自衰减修复技术和风险评价提供重要的理论基础。

敏感因子指数法［8］是一种可对垃圾填埋场渗滤液污染羽氧化还原特征区进行识别的有效方法。该方法主要通过确定敏感因子、建立基于特征区表征的量化方法、计算各敏感因子权重值、统计各特征区值并进行划分，最终实现对污染场地氧化还原特征区的识别。其中，由于每个敏感因子在不同特征区中所起作用和影响力不尽相同，需根据每个敏感因子在不同特征区中的重要程度赋予不同的权重。可以说，确定敏感因子的权重直接关系到其对识别结果的“贡献性”大小，是填埋场地下水污染过程识别技术体系建立的一个关键环节。

本文以确定敏感因子指数法中敏感因子的权重为目的，选用主观赋值法中的层次分析法［9］、客观赋值法中的变异系数法［10,11］以及组合权重法这三种方法来计算各敏感因子权重值，通过实际污染场地应用，对比分析得出三种方法中最适用于敏感因子指数法的一种权重计算方法。

1 材料与方法

1.1 方法建立

在垃圾填埋场污染地下水环境中，物理、化学和生物作用将伴随污染物的迁移和转化过程，其中生物作用在地下水自衰减过程中发挥主要作用。微生物利用地下环境中多种最终电子受体，通过好氧呼吸、脱氮、铁还原和产甲烷等代谢途径对有机污染物进行降解［12,13］，从而在地下水环境中形成一系列氧化还原特征区。当前，国内外已有研究表明［14-20］，垃圾渗滤液污染羽中确实存在氧化还原分区现象，而污染物在地下水环境中的自然衰减可能主要依赖于这些氧化还原环境。

在前人研究基础上，敏感因子指数法主要以热力学原理以及生物地球化学作用为依据［21-26］，针对地下水污染过程中主要发生的氧还原、硝酸盐还原、铁还原、硫酸盐还原以及产甲烷反应所产生的五个氧化还原特征区进行识别。方法的主要步骤如下：

首先，确定敏感因子。由于在自然系统中氧化还原反应很少处于平衡状态，因此，采用非平衡方法描述地下的氧化还原环境是有一定意义的，而通过监测不同微生物在代谢过程中所利用的最终电子受体（如O2、NO3-）、代谢最终产物（如Fe2+）和中间产物（如溶解性H2等的消耗量）等氧化还原灵敏性物质浓度的变化来描述氧化还原环境变化的最终电子受体作用（TEAPs）就是其中一种。针对上述五个氧化还原特征区，分别选取一种灵敏性物质作为敏感因子对各氧化还原特征区进行识别，这些敏感因子能够通过其在不同特征区中显著的变化规律来清楚表征各特征区中的氧化还原反应过程，并易于检测。因此，基于前期研究的多种灵敏性物质，本方法中选定溶解氧、亚硝酸盐、二价铁、硫化物以及二氧化碳作为敏感因子。

其次，建立基于氧化还原特征区表征的量化方法以及计算各敏感因子权重值。在不同的氧化还原特征区中发生了不同的氧化还原反应，导致参与反应的敏感因子的分布出现一定的规律性。基于各敏感因子在不同氧化还原特征区中的浓度变化规律，并依据各敏感因子在不同特征区中的重要程度赋予不同的权重值，将识别原理与数理统计方法相结合，建立一种基于特征区表征的量化方法，即将地下水污染羽下游区域划分为若干单元格，通过计算每个单元格内的产甲烷区值（M）、硫酸盐还原区值（S）、铁还原区值（F）、硝酸盐还原区值（N）、氧还原区值（O）来量化表征各氧化还原特征区，计算公式如下：

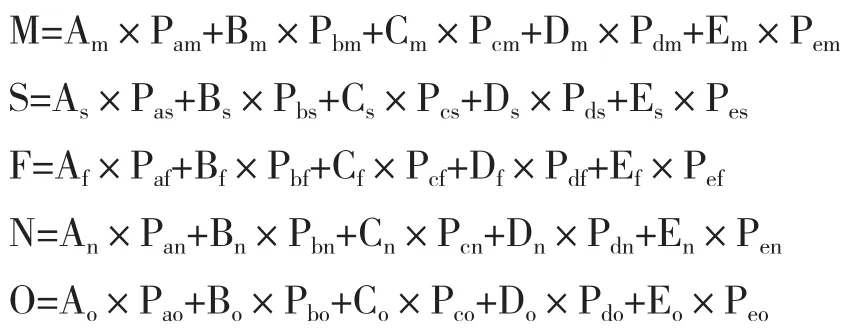
式中：M、S、F、N、O为各氧化还原特征区值；A、B、C、D、E依次表示二氧化碳、硫化物、二价铁、亚硝酸盐和溶解氧在各特征区中所占权重值；P为本方法中的敏感因子特征指数，当计算某一特征区值时，敏感因子实际浓度变化符合其在该特征区的客观规律时，P=1，不符合时，P=0。

然后，将每个单元格的各特征区值排序，区值越大表示该单元格区域的氧化还原环境特征与该特征区越符合，取最大区值即定为该单元格所属特征区。统计识别各单元格所属特征区，最后得到填埋场地下水污染过程识别各氧化还原特征区结果。

综上所述，在该技术方法中，各敏感因子的权重值的确定对于最后的识别结果具有至关重要的影响。本文重点针对敏感因子指数法中敏感因子的权重值计算方法开展研究，对比分析层次分析法、变异系数法以及组合权重法三种不同的权重计算方法对识别结果的影响，并通过实例进行验证，从而优选一种适用于敏感因子指数法的权重计算方法。

1.2 权重计算方法

目前，根据计算权重［27］时采用数据的不同来源，确定权重的方法一般可分为主观赋值法和客观赋值法两大类。主观赋值法，即计算权重所采用的数据主要由评估者根据经验主观判断得到，包括层次分析法等。客观赋值法［28］，即计算权重所采用的数据由各指标在分区识别过程中监测的实际数据得到，包括变异系数法等。这两类方法各有优缺点，主观赋值法客观性较差，但解释性强；客观赋值法确定的权重在大多数情况下精度较高，但有时会与实际情况相悖，对于所得到的结果难以给出明确的解释［29］。然而不论是主观法还是客观法，都具有一定的片面性。因此，还提出了一种主客观相结合的权重计算方法——组合权重法，将定性分析与定量分析相结合，减少主观分析的不确定性，使权重信息利用更全面。

1.2.1 层次分析法

层次分析法（ Analytic Hierarchy Process，AHP）［30］主要通过将复杂问题分解为若干层次和若干因素，对两两指标之间的重要程度作出比较判断，建立判断矩阵，再通过计算判断矩阵的最大特征值以及对应特征向量，得出不同方案重要性程度的权重，为最佳方案的选择提供依据［31］。其特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程定量化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法，尤其适合于对决策结果难以直接准确计量的场合。

1.2.2 变异系数法

变异系数法是根据评价指标的变异性来计算客观权重的一种数学方法，即利用评价指标的标准差与平均值之比来表示其变异量。指标取值差异越大，说明指标间差异越大，具有一定的科学性。此法利用各指标的变异系数来确定其权重，一方面充分利用了各指标本身监测数据所提供的信息，另一方面通过变异系数的归一化处理，可以防止指标之间因量纲不同而对权重产生影响，这样更能反映指标的相对重要程度［32］。求解步骤及计算结果如下：

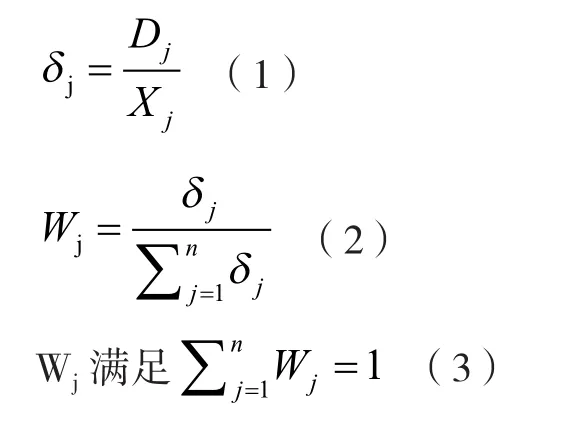
式中:Wj——评价指标j的权重；δj——第j个评价指标的变异量；Dj——评价指标j的标准差；Xj——第j个评价指标的平均值。

1.2.3 组合权重法

组合权重法把敏感因子的权重分为两类：主观权重和客观权重。主观权重是反映敏感因子不同属性对各氧化还原特征区的影响程度，客观权重是反映各区域敏感因子样本值差异信息对各氧化还原特征区的影响程度，组合权重法分别采用层次分析法和变异系数法确定这些权重，再用最小相对信息熵原理［33］把它们综合为组合权重［34］，该方法既可利用专家主观经验信息，又可挖掘各区域样本值的客观差异信息，权重信息利用全面。求解步骤如下：

步骤1:用层次分析法计算指标的主观权重W1j，j=1～m；

步骤2:用变异系数法计算指标的客观权重W2j，j= 1～m；

步骤3:综合指标的主观权重W1j和客观权重 W2j，可得组合权重 Wj，j=1～m。显然 Wj与W1j和W2j都应尽可能接近，根据最小相对信息熵原理用拉格朗日乘子法解得

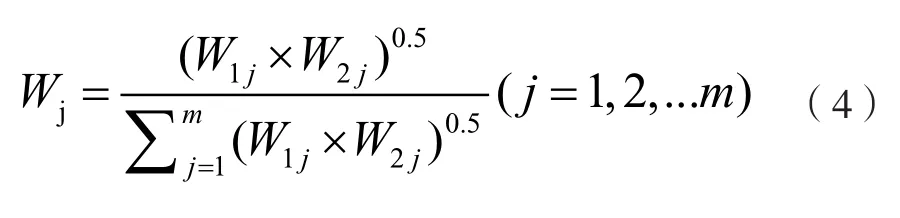
2 结果与讨论

2.1 方法应用

2.1.1 层次分析法应用

通过判断每个敏感因子在各特征区中的重要性确定判断矩阵，计算得出敏感因子在各特征区中所占的权重大小。

（1）确定层次结构。本文采用的层次结构设计为两层，上层是目标层，下层为指标层，即针对各个特征区建立层次结构模型，表征五个敏感因子对各个特征区的影响。

（2）构造判断矩阵。分析系统中各因素间的关系，依据机理特征对同一层次各元素关于上一层次中某一准则（即五个敏感因子对于各个特征区）的重要性进行两两比较判断，构造判断矩阵。判断矩阵的比较尺度Aij包括1、3、5、7、9，其含义分别为两个因素相比，1代表具有同样重要性；3表示一个因素比另一个因素稍微重要；5表示明显重要；7表示强烈重要；9表示极度重要。2、4、6、8均代表上述相邻判断的中值；Aij表示因素i与因素j比较的结果，因素j与因素i比较则为其倒数1Ai，各特征区的判断矩阵如下所示：

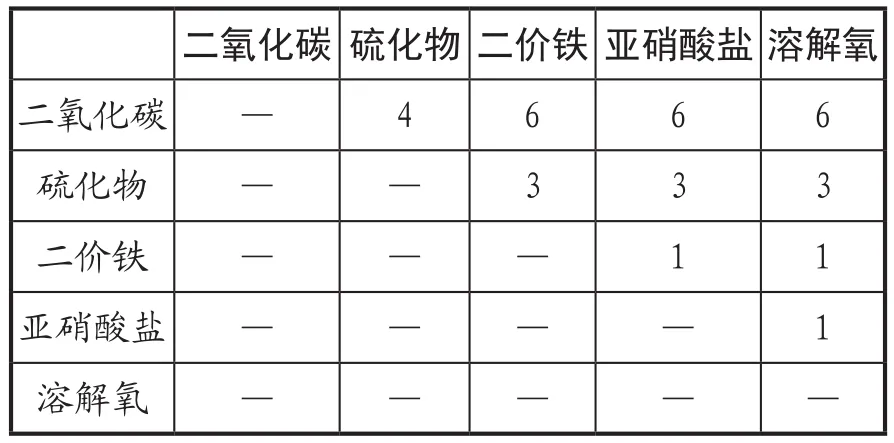
表1 产甲烷区判断矩阵

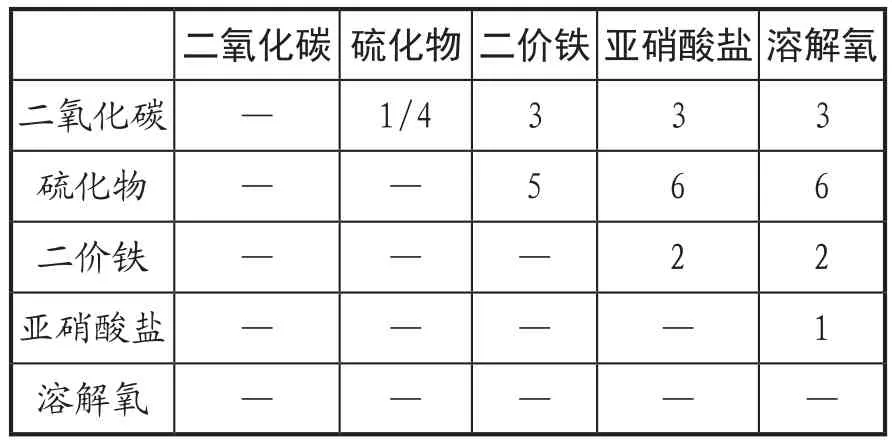
表2 硫酸盐还原区判断矩阵

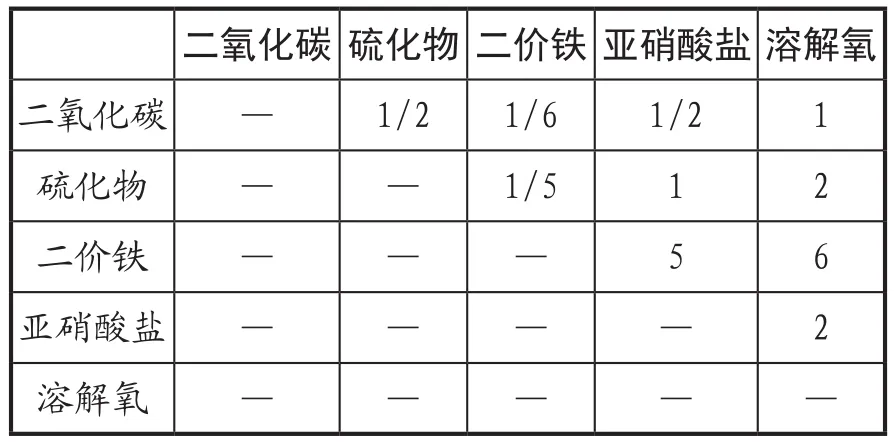
表3 铁还原区判断矩阵

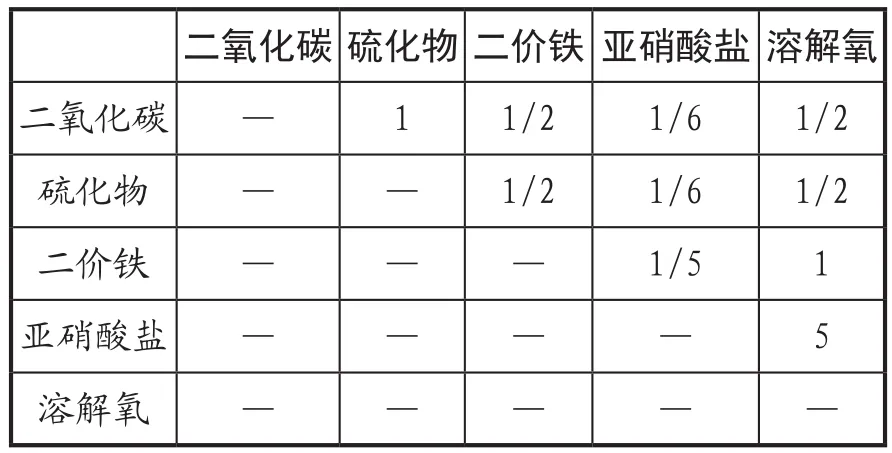
表4 硝酸盐还原区判断矩阵

表5 氧还原区判断矩阵

（3）运用yaahp层次分析法软件，利用上一步构造的判断矩阵对各个特征区内每个敏感因子进行权重值计算，并且通过检验计算，上述五个判断矩阵均具有满意的一致性。最后计算得出每个敏感因子在各特征区中所占的权重大小，见下表6。

表6 层次分析法计算权重值

2.1.2 变异系数法应用

本次研究应用于北方某垃圾填埋场地下水污染过程识别中，数据来源于场地各监测井内所取水样的监测数据，如下表7所示。对污染场地下游区域进行均匀布点取样，每个井位均需要对五个敏感因子浓度进行监测；根据检测值，依据上述求解公式（1-3），求得某一特征区中每个敏感因子的变异量及权重值；以同样步骤求出五个特征区内每个敏感因子所占权重值，如下表8所示。

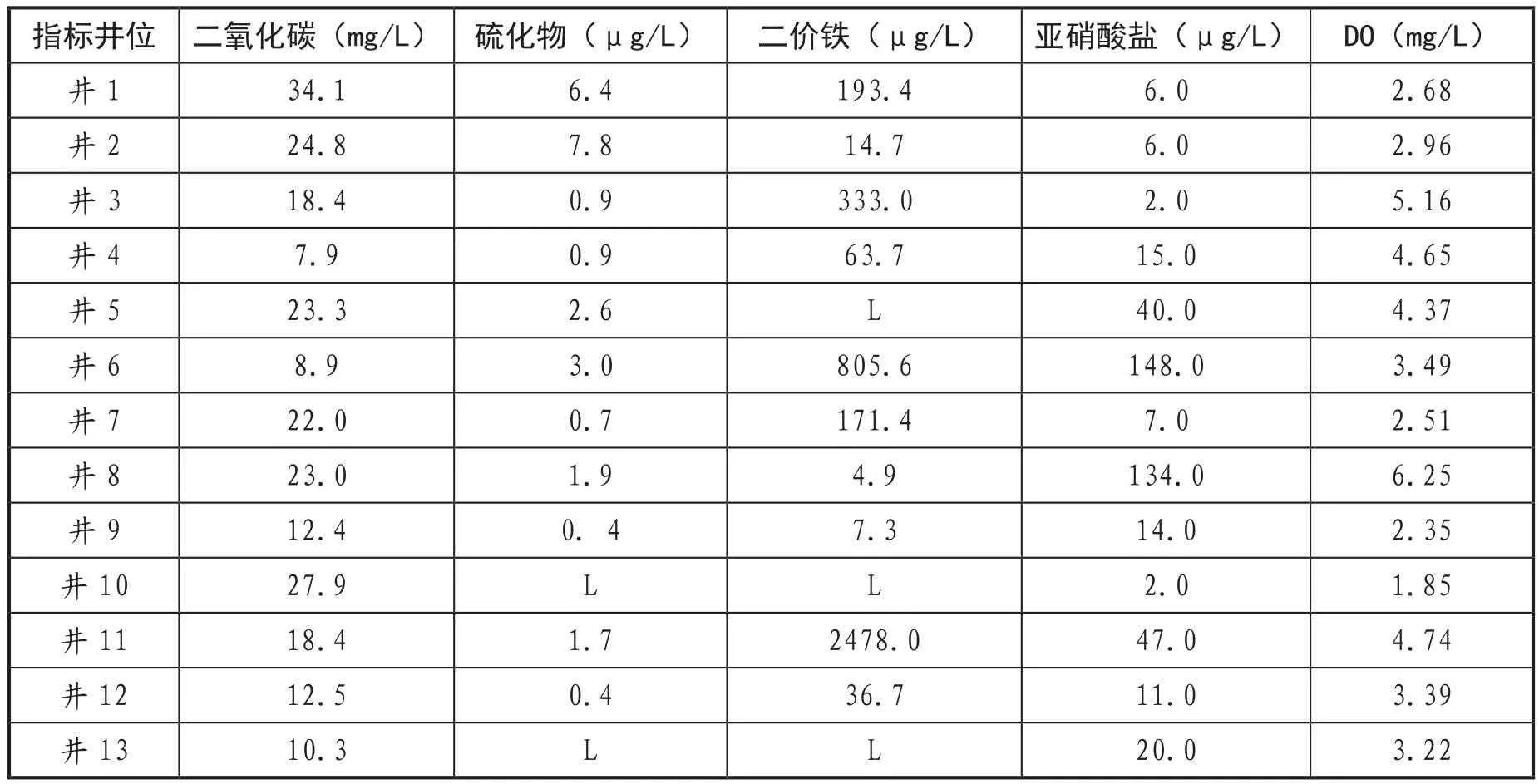
表7 垃圾填埋场监测数据

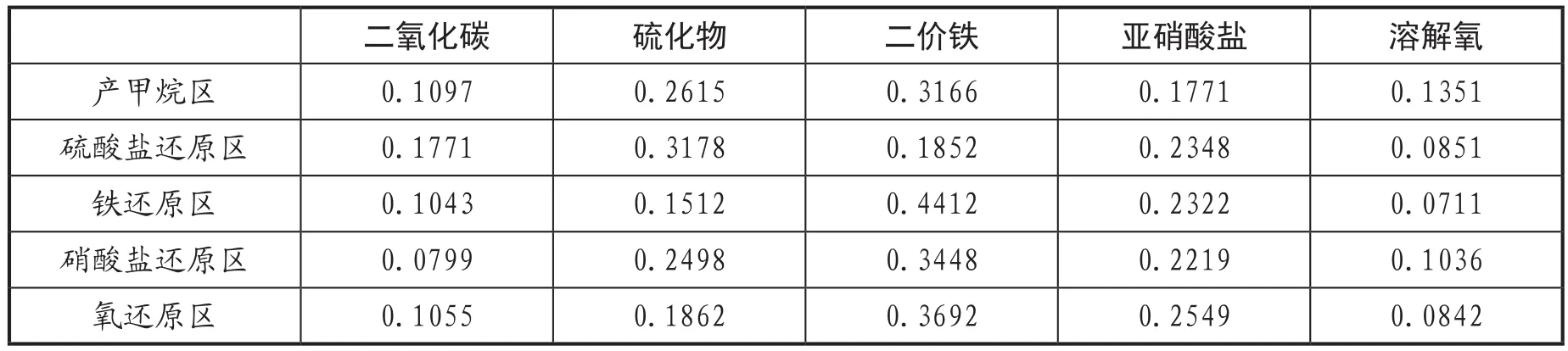
表8 变异系数法计算权重值

2.1.3 组合权重法应用

根据上述公式（4），综合敏感因子的主观权重值（表6）和客观权重值（表8），计算求得每个敏感因子在各特征区中所占权重值，如下表9所示。

表9 组合权重法计算权重值

2.2 结果分析

将上述三种权重计算方法得到的每个敏感因子在各特征区中所占权重值代入敏感因子指数法中，得到北方该垃圾填埋场下游区域的氧化还原特征区分区示意图，分别如下所示：

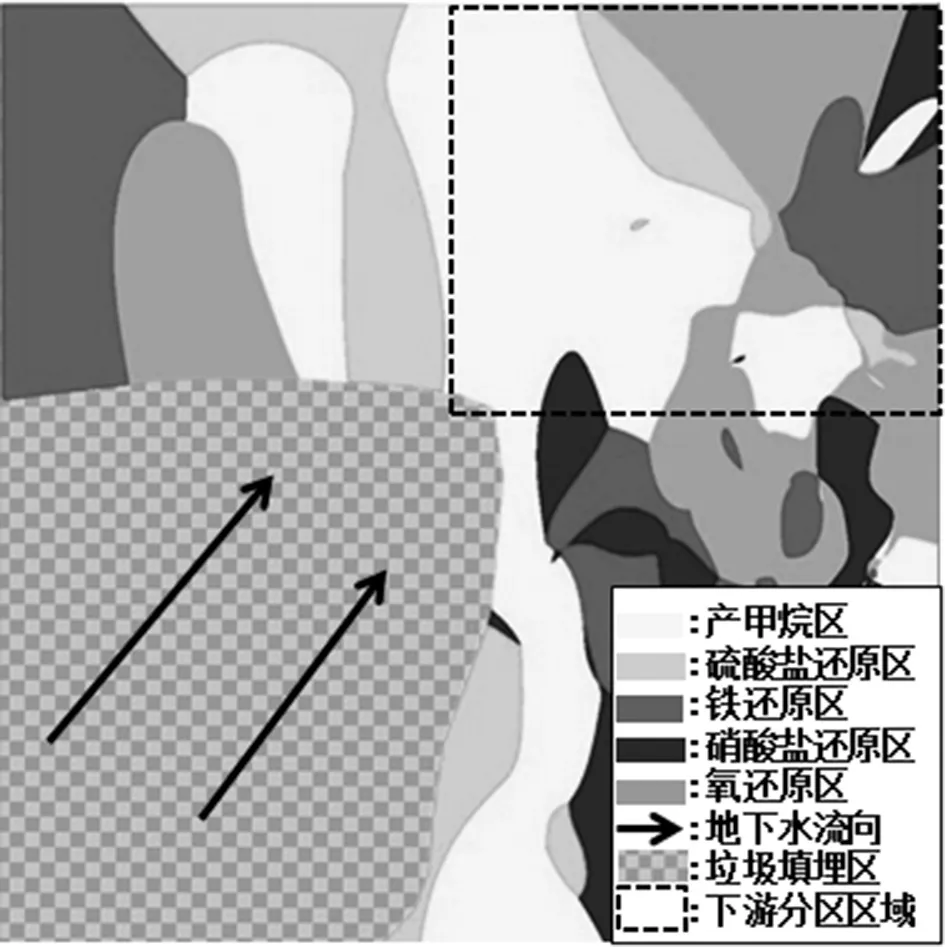
图1 层次分析法识别各氧化还原特征区分布图

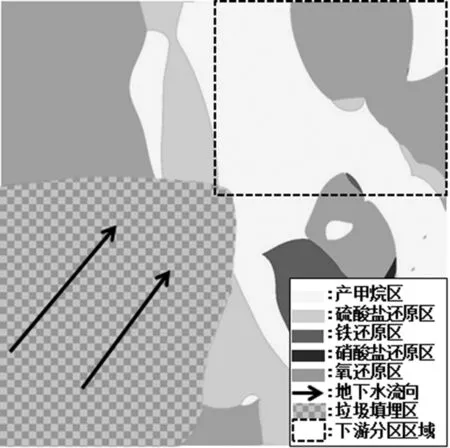
图2 变异系数法识别各氧化还原特征区分布图

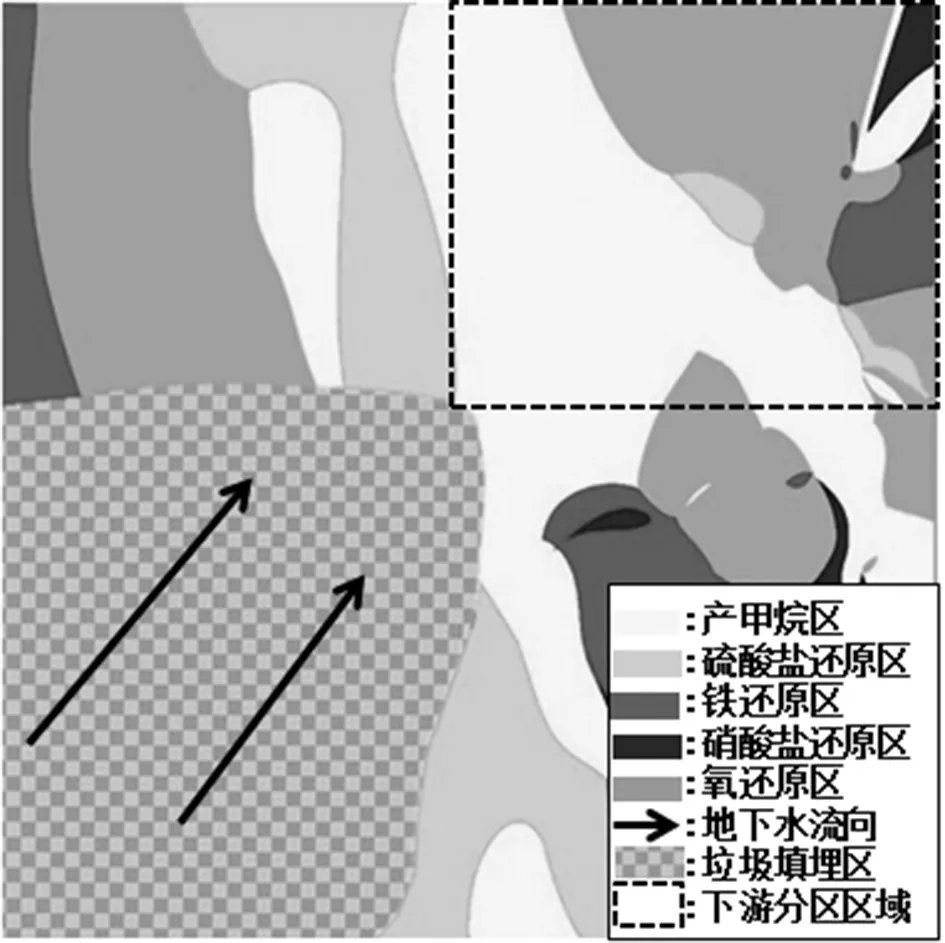
图3 组合权重法识别各氧化还原特征区分布图

从以上三种权重计算方法所得的分区结果可以看出，层次分析法与组合权重法得出的分区结果接近，而变异系数法所得的各特征区分布结果与另两种方法所得结果差异则较为明显。依据地下环境中微生物的最终电子反应排序来看，在垃圾填埋场下游污染羽在地下水流向上，各特征区分布依次应为产甲烷区、硫酸盐还原区、铁还原区、硝酸盐还原区以及氧还原区。该场地监测地下水流向为西南流向东北，沿着场地地下水流向来看，产甲烷区和硫酸盐还原区密切相关，因为他们有相似的氧化还原电位，要严格区分二者比较困难，从这三个分区结果中也可以看出这两个特征区可能有一定程度的重叠，以及交替出现的情况。

在变异系数法的分区结果图中，产甲烷区和硫酸盐还原区后出现了氧还原区，而铁还原区和硝酸盐还原区几乎不存在。对于该场地本身即为高铁环境而且周围遍布民居、养殖场以及农田这种情况来说，最终电子受体Fe3+以及NO3-在地下水环境中应普遍存在，在渗滤液污染地下水环境过程中，铁还原以及硝酸盐还原反应也应显著存在。此外，该客观赋值法采用敏感因子的实际监测数据进行计算，监测数值间的差异较大，其所占权重值亦是，而最后却未出现这两个特征区，表明该权重计算方法所得的分区结果可能无法完全地反映该场地地下水污染过程中各氧化还原特征区分布情况。

而将层次分析法和组合权重法两者分区结果比较来看，氧还原区的异常分布是共同存在的，这可能是由于下游某些局部区域民井较多，使用量较大，对局部的地下水流向和水位波动均有扰动，而这两个因素可能会对氧化还原特征区产生影响，导致该区域被垃圾渗滤液污染的程度较轻所致。此外，层次分析法依据专家经验打分，相较于组合权重法，其分区结果较为混乱，而组合权重法同时结合主观与客观分析，所得出的特征区分布基本与实际情况吻合。因此，选定组合权重法作为敏感因子指数法中计算权重的方法较为合理。

3 结论

组合权重法把敏感因子的权重结构分解为反映敏感因子不同属性对各氧化还原特征区影响程度的主观权重和反映各区域敏感因子样本值差异信息对各氧化还原特征区影响程度的客观权重，分别采用层次分析法和变异系数法通过最小相对信息熵原理把它们综合为组合权重。这种权重计算方法既可充分挖掘评价指标权重结构中的专家主观经验信息和各敏感因子样本值的客观差异信息，其分区结果也更符合垃圾填埋场地下环境中微生物作用规律，比较适用于对垃圾填埋场地下水污染过程进行识别的敏感因子指数法。