基于抽样和变邻域搜索的随机共享单车重平衡问题

贾永基， 恽博文， 许媛媛

(东华大学 旭日工商管理学院， 上海 200051)

随着我国经济的迅猛发展，交通运输需求快速增加，未来仍将长期呈现增长态势，这导致交通运输系统的碳排放所占份额越来越大。在2021年全国两会上，“碳达峰”与“碳中和”首次被写入政府工作报告。为了如期实现“双碳”目标，降低交通系统碳排放，须大力推广零排放的共享单车系统。近20年来，共享单车作为一种低碳、环保的短途出行方式在全球范围内得到广泛应用，在缓解交通拥堵、构建绿色出行体系方面做出了极大贡献[1]。然而，随着共享单车规模的不断扩大，供需不匹配现象愈加严重，在加大企业运营成本的同时，降低用户满意度，这将极大阻碍共享单车行业的健康发展。因而实施有效的共享单车供需重新匹配操作，即共享单车重平衡问题(bike-sharing rebalance problem，BRP)[2]，显得尤为重要。

在目前的研究成果中，所有参数都已知的确定性BRP研究已较为成熟[3]，而在实际运营场景中，客户需求、行驶时间等参数都不可避免地会出现波动，因而随机BRP逐渐引起研究人员的重视。目前随机BRP的主要求解方法大致可分为4类：需求预测、马尔可夫决策过程、滚动时域和随机规划。Zhang等[4]在预测单车库存和用户需求的基础上建立BRP模型。靳文舟等[5]基于用户预约数据进行需求预测，构建了考虑用户满意度的最小化总成本的BRP模型。陈菁等[6]基于小波神经网络预测区域需求量构建BRP模型。Federico等[7]利用历史数据来预测共享单车网络状况并在必要时采取重平衡操作。Pan等[8]建立了基于马尔可夫决策过程的BRP模型，并提出一种基于确定性策略梯度算法的深度学习算法。Legros[9]则使用马尔可夫决策过程开发一种可实施的决策支持工具，帮助运营商在任何时间决定站点优先级及单车库存。Zhai等[10]同样利用马尔可夫决策过程和线性规划方法来解决共享单车车队规模和BRP问题。董红召等[11]加入模糊时间窗约束，以站点满意度最大为目标建立公共自行车系统调度模型，采用滚动时域算法来求解该模型。Shui等[12]也采用滚动时域获得多个阶段的静态子问题，使用改进的人工蜂群算法和路线截断算法来优化每个阶段的重平衡车辆路径。Maggioni等[13]考虑共享单车随时间变化的随机需求，提出两阶段和多阶段随机规划模型，以确定在次日服务开始时每个站点的最优单车数量。

现实BRP系统中，客户随机取车、还车，使得各站点的单车数量时刻处于变化中，因而无法提前获得较准确的预测数据，导致基于需求预测的重平衡模型的计算结果偏离实际值较大。马尔可夫决策过程计算复杂，因而其不适合大规模的实际问题求解。滚动时域采用“wait and see”策略等待随机需求的确定值出现，导致重平衡的时效性较差。随机规划是一种事前策略，同时不要求事先知道所有参数的确定值，因而具有更大的使用范围。据笔者所知，目前还没有文献使用随机规划方法来研究需求随机的共享单车重平衡问题(bike-sharing rebalancing problem with stochastic demands，BRPSD)。

使用共享单车企业的历史数据，可以估计客户随机需求的分布概率。为了简化计算，本文假设客户需求的分布概率是已知的，因而可以使用拉丁超立方抽样(Latin hypercube sampling，LHS)来生成一系列具有给定概率的离散场景来表示客户需求的随机性。在每个场景下，客户需求是固定不变的，因而可以使用常规启发式算法(例如变邻域搜索算法)进行求解。LHS是一种基于蒙特卡洛模拟的方法。Löhndorf[15]研究流行的随机场景生成方法，指出蒙特卡洛方法是目前最流行的方法，但其需要大量样本以确保随机变量概率分布的准确近似，该缺陷可以使用LHS加以缓解。Nikzad等[16]已证实基于LHS获得的结果更接近基于大样本获得的结果，且在相同数量的场景中，LHS比蒙特卡洛方法可获得更准确的近似值。因此，本文采用LHS来生成一系列随机场景。此外，本文重新定义共享单车站点的平衡状态，提出了表示站点平衡状态的平衡区间概念，给出了衡量站点重平衡程度的重平衡效应度函数。在此基础上，建立BRPSD的两阶段随机规划模型，并提出了求解该模型的基于LHS的变邻域搜索算法。

1 问题描述与数学模型

1.1 问题描述

在共享单车系统中，由于单车的单程性所导致的“潮汐现象”会使单车供需不匹配，从而导致用户满意度和单车利用率的下降，不利于共享单车行业的可持续发展。共享单车重平衡是指利用运输车辆将单车从过剩站点运往不足站点，即重新在站点之间分配单车以达到供需平衡。如何经济、高效地实现共享单车重平衡也就成为共享单车行业亟待解决的关键问题。

在共享单车企业实际运营中，为明确工作职责，往往将单车服务区域划分成多个不关联的子区域，每个子区域只由一辆运输车单独进行重平衡操作。考虑到随机重平衡问题的复杂性，不失一般性，本文只考虑一辆运输车辆的情形，且假设每个站点只能被服务一次。BRPSD问题可以描述为：车辆从车库出发，依次访问处于不平衡状态的共享单车站点，通过取车或卸车操作使得所有站点趋于平衡状态，最后返回车库，同时考虑车辆行驶距离的最小化和重平衡效用度期望的最大化。

本文所使用的决策变量和符号如表1所示。

表1 决策变量和符号

1.2 平衡区间和重平衡效应度

现有研究多将共享单车站点的平衡状态设为一个平衡点，但由于客户取车、还车活动的随机性，站点的单车数量是波动的，因而平衡点的设置使得重平衡操作不具有稳定性，提高了重平衡成本。因此，本文将站点的平衡状态由平衡点改为平衡区间[14]，如图1所示，其中aj是站点j的当前单车数量，bj和[(1-θ)bj,(1+θ)bj]分别是其平衡点和平衡区间。当站点的单车数量在其平衡区间内时，该站点就处于平衡状态。即使站点单车数量由于客户活动出现了随机波动，只要波动范围不超过平衡区间阈值，就无需进行重平衡操作，这可以大大减少共享单车系统的重平衡需求，从而提高共享单车企业的重平衡效率。

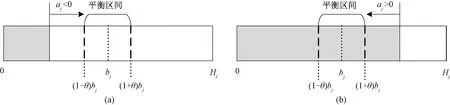
图1 共享单车系统的平衡区间

由于站点单车数量的随机性，本模型不强制要求所有站点在被服务后都处于平衡状态，而采用重平衡效用度[14]来衡量重平衡操作的效益，如图2所示。在重平衡操作后，若站点j的单车数量处于平衡区间[(1-θ)bj,(1+θ)bj]内，那么其重平衡效用度为1。当单车数量小于平衡区间下界(1-θ)bj或大于平衡区间上界(1+θ)bj时，其重平衡效用度随aj与平衡区间差值的逐渐增大而逐渐减小。

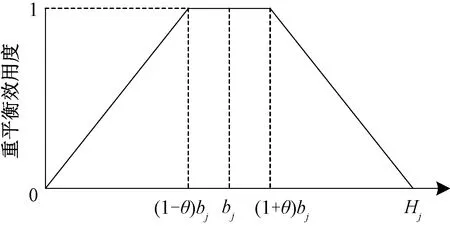
图2 站点的重平衡效用度

1.3 两阶段随机规划模型

基于LHS的两阶段随机规划模型的第一阶段为运输车辆路径优化模型，最大化共享单车系统的总效益；第二阶段基于第一阶段所获得的车辆路径信息，最大化重平衡效用度期望。第二阶段基于第一阶段的路径信息，又影响着第一阶段的路径决策。

第一阶段模型(P1)：

(1)

s.t.

(2)

(3)

∀S⊆V,2≤|S|≤n-1

(4)

xij∈{0,1} ∀i,j∈V,i≠j

(5)

其中：式(1)表示共享单车系统的总效益，重平衡操作产生正效益，系数为ε1，而车辆行驶成本产生负效益，系数为ε2；式(2)表示每个站点只能被访问一次；式(3)表示流量平衡；式(4)用于消除子回路；式(5)表示决策变量的取值范围。

第二阶段模型(P2)：

(6)

(7)

∀j∈N,ω∈Ω

(8)

lj,ω2=lj,ω1-sj,ω++sj,ω-∀j∈N,ω∈Ω

(9)

sj,ω+×sj,ω-=0 ∀j∈N,ω∈Ω

(10)

(11)

(12)

(13)

sj,ω+，sj,ω-，fij,ω≥0 ∀i,j∈V,i≠j,ω∈Ω

(14)

其中：式(6)表示最大化随机场景下的重平衡效用度期望；式(7)表示场景ω下运输车辆的装载量不大于车辆容量；式(8)表示场景ω下车辆服务站点前后的装载量之差等于站点被满足的单车数量；式(9)表示场景ω下站点被服务前后的单车数量之差等于站点被满足的单车数量；式(10)表示场景ω下站点不能同时具有取车和卸车需求；式(11)表示场景ω下的站点重平衡效用度；式(12)表示决策变量sj,ω+不能超过车辆访问站点时的剩余容量；式(13)表示决策变量sj,ω-不能超过车辆访问站点时的装载量；式(14)表示决策变量的取值范围。

2 基于LHS的变邻域搜索算法

2.1 算法流程

BRPSD模型的解由两部分决定：第一阶段的车辆路径和第二阶段一系列随机场景下的重平衡需求。其中，车辆路径可表示为(0,i1,i2,…,in,0)，其中0是车库，而i1,i2,…,in是车辆所访问站点的一个排列。通过改变站点的顺序，可以获得车辆的不同行驶路径。显然，可以通过求解一个旅行商问题来获得第一阶段的最优车辆路径。本文设计了基于拉丁超立方抽样的变邻域搜索(Latin hypercube sampling based variable neighbourhood search，LHS-VNS)算法来求解BRPSD问题，该算法流程如图3所示。

图3 LHS-VNS算法流程图

首先，采用LHS生成一系列随机场景，每个场景都具有相同的概率。接着，使用商业优化软件CPLEX求解第一阶段模型P1，获得车辆最优路径。然后，将车辆最优路径代入第二阶段模型P2，求解该路径在所有场景下完成重平衡操作后达到的重平衡效用度期望的最大值。如果没有达到停止条件，则利用变邻域搜索(variable neighbourhood search，VNS)算法来获得新的车辆路径，并将其代入模型P2进行计算，否则结束迭代，输出车辆最优路径及目标函数F的值。

2.2 随机场景生成

选择适当的场景生成方法并确定最佳场景数是求解BRPSD的首要问题。为了获得好的场景分布，本文使用LHS来生成随机场景。LHS是一种分层随机抽样，具有均匀分层的特性，可以在较少抽样的情况下保证每个变量范围的全覆盖。假设有k个变量x1,x2,…,xk,要从规定的区间中取出N个样本，首先计算每个变量的累积分布，并将其分成N个相同的小区间，随后从每个区间中随机选择一个值，如图4所示，这样每一个变量都会获得N个值，最后将不同变量的值进行随机组合，从而获得所需样本。在进行抽样时，为了简化计算，本文假设每个抽样的概率都是相同的。

图4 拉丁超立方抽样

2.3 站点重平衡需求计算

在第一阶段结果的基础上，第二阶段求解一系列随机场景下共享单车站点的重平衡需求。设站点j的最佳单车数量L=0.5Hj，其在场景ω下的重平衡需求计算过程如图5所示。如果lj,ω1L，站点j需要取走单车，若此时车辆剩余容量足够，则将多余单车移走使得站点j的单车降低到最佳数量L，否则将车辆装满即可。

图5 场景ω下重平衡需求计算过程

2.4 VNS算法

Mladenovic等[17]在1997年提出VNS算法，该算法容易实现，通用性强，目前已经被广泛用于求解各类组合优化问题[18]。本文采用包括3种邻域结构(见图6)的VNS算法来生成新的运输车辆路径，每次随机选择其中一种邻域结构来执行。(1)点插入：随机选择一个站点，将其从原始位置上移除，并插入到另外一个随机位置，如图6(a)所示。(2)节点交换：随机选择两个站点，交换其位置，如图6(b)所示。(3)2-opt：随机选择两个站点，将它们之间的站点逆序，如图6(c)所示。

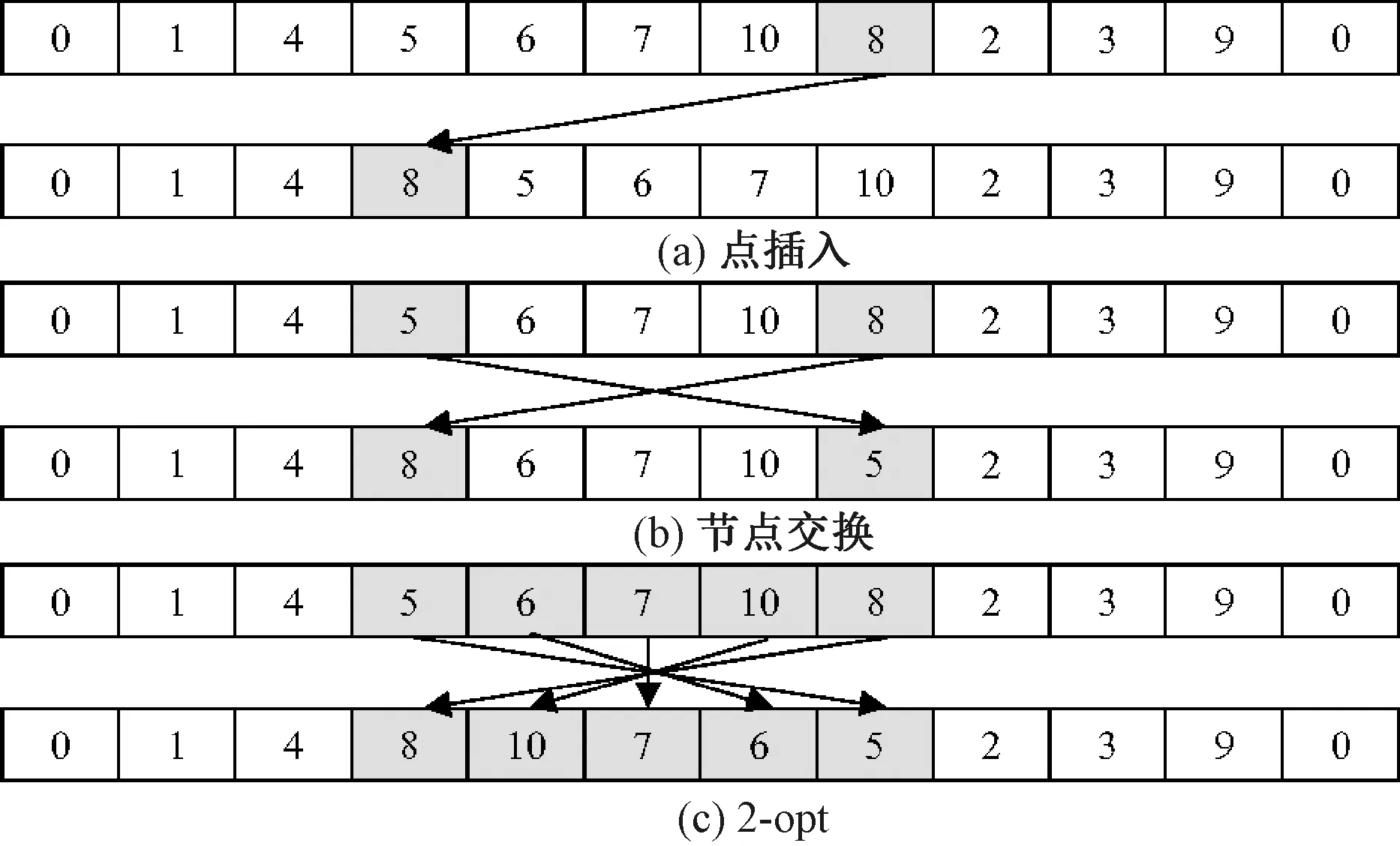
图6 邻域结构

3 仿真测试

使用MATLAB R2014b软件编程实现LHS-VNS算法，所有试验都是在Intel Core i5-8265U和8 GB RAM的笔记本电脑上运行。

3.1 测试算例与参数设置

为测试LHS-VNS算法的有效性，随机生成站点规模分别为15、20、25和30的4组测试实例，每组3个算例。站点的坐标是在纬度31.17°～31.23°和经度121.37°～121.45°内随机生成的，车库位于区域中心，其坐标为(31.20°，121.41°)。站点容量均为100。假设客户需求服从正态分布，所有算例中客户需求的均值和标准差如表2所示。其他参数如下：平衡区间阈值θ=0.2，站点平衡区间均为[40,60]；运输车辆容量为50，出库时的装载量为10；系数ε1和ε2分别取0.5和0.8；抽取的样本数分别为75、100、125和150，迭代次数为10 000。

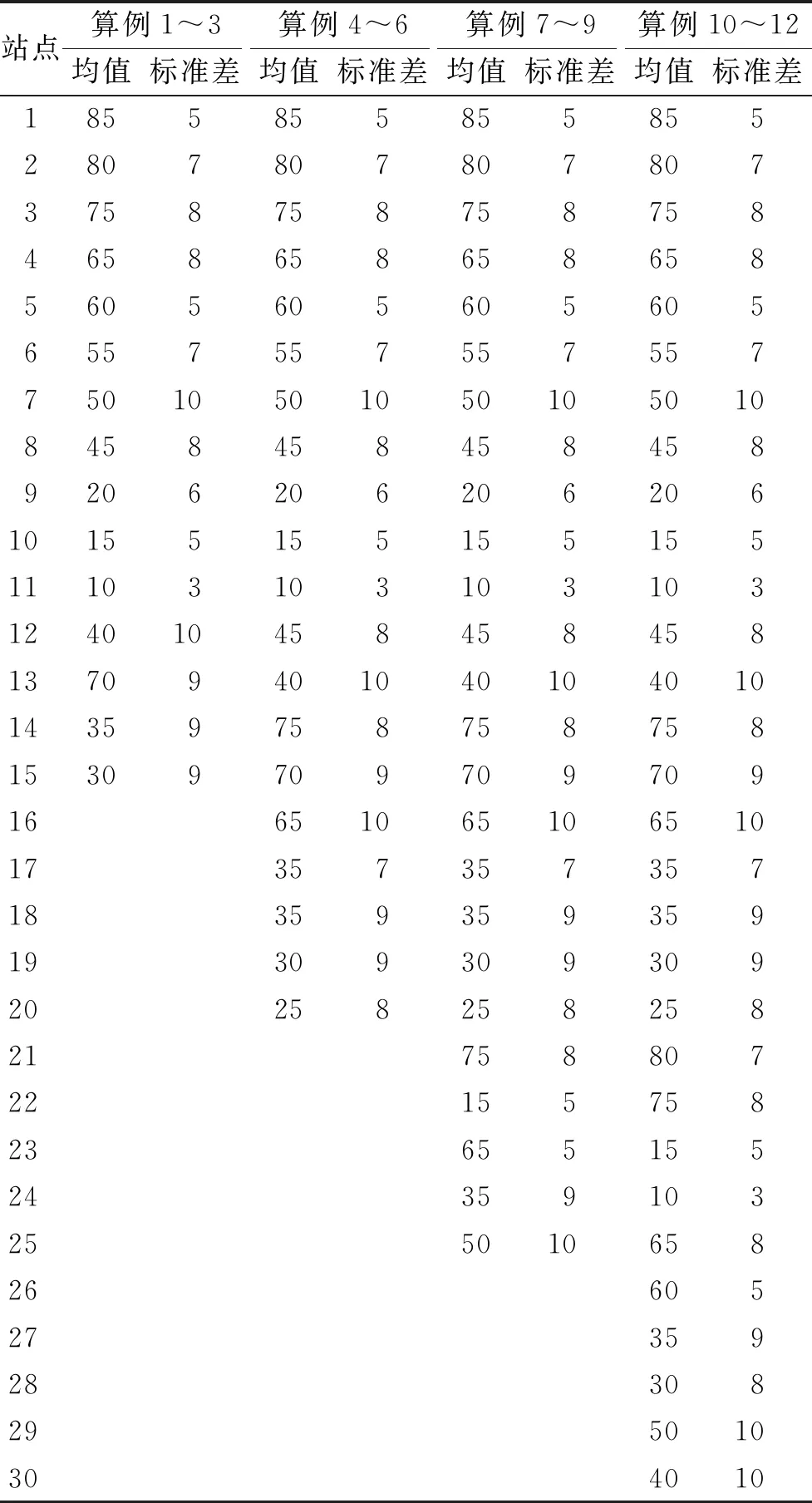
表2 客户需求的均值与标准差

3.2 场景生成效果分析

本节计算LHS所获得样本的均值和标准差，以及与所设定的均值及标准差的绝对差，并与蒙特卡洛抽样的结果进行了对比。算例1的对比结果如表3所示，样本量均为75。由表3可以看出，LHS所获样本的均值绝对差和标准差绝对差的绝大部分都优于蒙特卡洛抽样，且LHS样本的均值与设定均值的绝对差值都小于0.10，标准差的绝对差值都小于0.40，而蒙特卡洛抽样的波动较大，其均值绝对差值和标准差绝对差值最高都超过了1.00。由此说明LHS的抽样效果优于蒙特卡洛抽样。

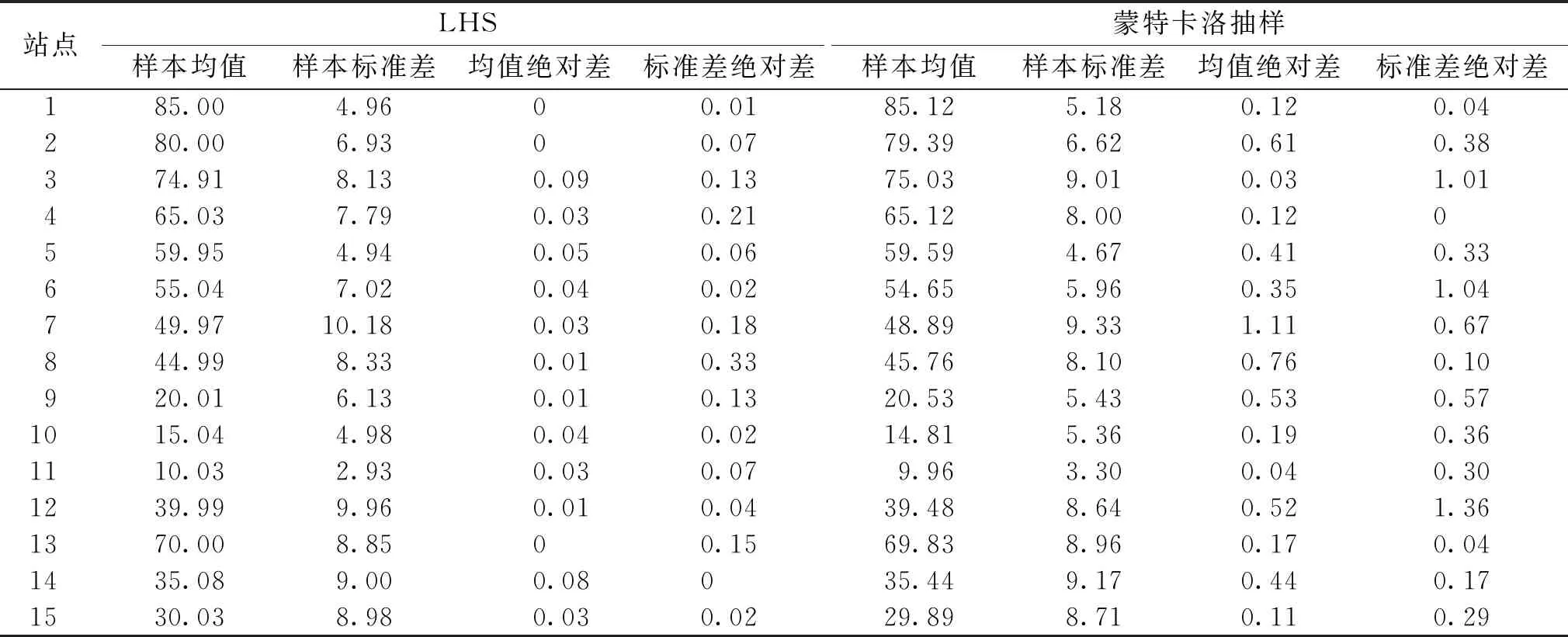
表3 LHS与蒙特卡洛抽样对比结果

将算例6的样本量分别设为50、75、100、125、150和175，LHS的抽样结果如表4所示。由表4可以看出，随着样本量的增大，F的最大值趋于稳定，所有样本的车辆路径均相同，但抽样运行时间却随着样本量的增加而增加。这也验证了LHS的优势，可以使用较小的样本量来生成随机场景，在缩短计算时间的同时获得大致相同的计算结果。

表4 样本量分析

3.3 求解结果分析

基于样本量为100的一系列随机场景，每个算例均运行10次，所求得目标F的最大值、最小值、均值和标准差如表5所示。由表5可以看出，同一规模算例的F均值和运行时间均相差不大，而规模越大的算例，其F值和运行时间越大。此外，所有算例的标准差都小于1.00，说明算法具有良好的稳健性，其中小规模算例1和算例3的标准差为0，说明这两个算例10次的运算结果均相同。

表5 求解结果

为了进一步验证本文算法求解大规模算例的性能，采用同样的方法生成站点规模分别为50(算例13～15)和60(算例16～18)的两组算例。设样本量为100，每组算例均运行10次的求解结果如表6所示。由表6可以看出，所求得结果的稳定性可以接受，但运行时间差异较大。

表6 大规模算例求解结果

4 结 语

针对需求随机的共享单车重平衡问题，引入平衡区间代替平衡点来表示站点的平衡状态，提出了衡量站点平衡程度的重平衡效应度，通过LHS得到一系列具有相同概率的随机场景来表示客户的随机需求，提出了BRPSD两阶段随机规划模型的数学表达。由于该问题是NP-hard问题，因此提出了求解该模型的LHS-VNS启发式算法。为了验证该算法的有效性，设计了多种规模的测试算例，测试结果表明：(1)与蒙特卡洛抽样相比，LHS的抽样效果更优也更稳定，其运行时间更短；(2)LHS-VNS可在较短时间内获得BRPSD的稳定结果，具有良好的稳健性。

未来的研究方向：一方面可以关注提高LHS-VNS的运行效率，以缩短较大规模算例的运行时间；另一方面可以研究使用多辆运输车同时进行重平衡操作，从而扩展本文提出的BRPSD模型。