基于模态参与因子的无轴承开关磁阻电机振动分析与抑制

朱伟明 ，杨 艳，刘泽远，刘程子

(南京邮电大学 自动化学院、人工智能学院，南京210046)

0 引 言

电机作为动力原件广泛用于工业和生活的方方面面，世界电能的70%以上是由各类电机消耗[1]。然而电机在提供动力的同时也会带来较大的振动和噪声，这一结果将直接影响电机的使用寿命。为此，改善电机的振动噪声性能已成为评价电机品质的一个重要指标[2-4]。目前，电机噪声通常包括电磁噪声、机械噪声以及空气动力噪声[5-8]，机械噪声主要由工艺误差引起，而空气动力噪声很小，故一般可以忽略不计。

开关磁阻电机电机(Switched Reluctance Motor,SRM) 由于其双凸极结构，外加导通相定子极受脉动的径向磁拉力作用，相比于其他传统电机，SRM的振动噪声尤为突出，较大的振动噪声阻碍了其应用场合和推广[9-11]。针对SRM振动噪声大的问题，国内外学者对此做了大量的研究。目前这一研究的关注点主要集中在两个方面，一方面是从电机本体结构入手来抑制振动，比如文献[12-13]采用扭曲定转子的方法，延展了定子凸极表面，该方法相比于传统电机具有很好的减振效果。文献[14-15]对转子侧开槽后电机径向电磁力进行分析，得到该方法对径向电磁力具有抑制作用，但是同时会对电机的转矩输出有一定影响。文献[16-19]表明合理改变绕组连接方式可以有效减小SRM的振动。文献[20-21]通过优化定转子凸极的倾斜度来抑制的电机振动。另一方面，学者们从优化控制策略的角度来降低SRM振动噪声也取得了一定的成果。文献[22-23]英国谢菲尔德大学的Liu X.使用电流滞环控制和空间向量脉冲宽度调制的方法对6/4极SRM相电流进行直接控制，通过验证表明电机振动噪声可以得到明显抑制。文献[24]内布拉斯加林肯大学Ma C.使用差异进化算法优化相电流波形，降低了径向力谐波幅值，抑制了电机的振动噪声。文献[25]孙剑波、詹琼华等人将直接转矩控制与两步换相法相结合，兼顾了SRM转矩脉动和振动噪声。文献[26-28]采用两步换相法有效抑制了SRM的振动。文献[29]采用上下双层电机模型，上下双层通入具有相位差的电流并轮流导通，既能输出较高转矩，又能降低电机振动。

无轴承开关磁阻电机(Bearingless Switched Reluctance Motor,BSRM) 是在SRM的基础上发展而来，同样面临振动噪声问题。虽然对于BSRM的振动噪声研究没有SRM成熟，但是也取得了阶段性成果。文献[30]和文献[31]通过分析推导出了考虑磁饱和的径向电磁力数学模型，为研究BSRM振动噪声奠定了基础。针对控制策略方面的研究，文献[32-33]通过分析主绕组方波电流控制、最小磁势控制和平均悬浮力控制等策略，指出不同的控制策略对电机振动的抑制效果也不同，其中最小磁势控制是一种利于BSRM减振降噪的控制策略。针对BSRM转子不平衡引发的振动问题，文献[34-35]从转子偏心补偿角度进行了振动方面的深入研究，并取得了一定进展。文献[36]通过实时控制BSRM悬浮绕组，以达到减振目的。

本文研究的12/8极BSRMWR，其转子齿是将传统BSRM的转子齿由原来的15°变为30°，这一改变解决了BSRM转矩和悬浮力之间的强耦合问题，大大简化了电机的控制策略。然而，BSRMWR作为传统BSRM结构上的一种演变，其双凸极结构及开关供电方式并未改变，故BSRMWR仍然存在较大的振动噪声问题。文献[37]在研究BSRMWR发电运行控制策略时，发现所采用的控制策略有一定效果的减振作用。然而，专门针对该电机振动噪声的研究目前仍相对甚少，基本处于空白状态。本文采用三维有限元法，从电机外壳优化的角度去考虑降低BSRMWR振动的合理策略，结合模态参与因子分析了BSRMWR的振动性能。基于此对壳体添加不同方向的加强筋来进行优化，通过优化前后分析比较，得到对其减振有利的加强筋壳体模型结构。

1 模态参与因子理论分析

在SRM电机实际运行中，一般只是少数几个振动模态被有效激发出来，因此可以用多个单自由度振动系统的线性叠加来模拟电机的实际振动[38-39]。BSRMWR是在SRM和BSRM的基础上演变而来，为了简化分析，处理方便，在研究BSRMWR振动系统时也可以对其进行线性等效模拟。

BSRMWR可等效为一个多自由度系统，对于多自由度振动系统，其动力学方程为

(1)

([K]-ω2[M]+jω[C]){X(ω)}={F(ω)}

(2)

由于矩阵[M]、[C]和[K]中存在非零的非对角元素，因此式(2)是一组具有耦合项的方程组。运用模态矩阵作为变换矩阵，可进行坐标变换。其中模态矩阵和模态坐标如式(3)和(4)所示。

[φ]=[φ1,φ2,…,φN]

(3)

q={q1(ω),q2(ω),…,qN(ω)}T

(4)

根据线性化假设，令{X(ω)}=[φ]{q}代入式(2)，得模态坐标下的运动方程：

([K]-ω2[M]+jω[C])[φ]{q}={F(ω)}

(5)

将式(5)两边左乘[φ]T，利用振型矩阵对质量矩阵和刚矩阵的正交性，并对阻尼矩阵对角化，得：

[φ]T([K]-ω2[M]+jω[C])[φ]{q}=[φ]T{F(ω)}

(6)

由式(6),得到第r阶的解耦方程：

([Kr]-ω2[Mr]+jω[Cr]){qr}=[φ]TF(ω)

(7)

式中,[Mr]、[Cr]、[Kr]分别为第r阶的模态刚度、模态质量和模态阻尼。在第r阶模态坐标的响应为

(8)

式中,qr为第r阶模态坐标，其物理意义表示各阶模态振型φr对系统振动响应的贡献的度量，即模态参与因子[40-41]。

BSRMWR激励力F(t)即为径向磁拉力，该径向电磁力作用于电机定子齿传递到电机定子及机壳上，是引起电机振动的主要原因，故求解分析BSRMWR的径向磁拉力是研究振动响应的首要条件。由于振动总响应是各阶模态响应的叠加，因而对BSRMWR进行模态分析也是必不可少的重要环节。

2 BSRMWR的径向电磁力分析

12/8极BSRMWR本体结构如图1所示，共有12套绕组，各相齿极绕组之间均独立控制。每个定子凸极上只有一套绕组，通过控制各相定子齿极上的绕组电流大小，便可产生不对称气隙磁密，从而控制径向磁拉力，以实现转子的悬浮运行。图2所示为BSRMWR双相导通工作原理图，处于电感上升区的一相提供转矩，处于电感平顶区的一相提供悬浮力。

表1为12/8极BSRMWR样机的主要参数，由此建立图3所示JMAG仿真模型。

表1 BSRMWR模型主要参数

BSRMWR绕组采用的外电路是不对称半桥，结合BSRMWR的工作原理，在JMAG电磁仿真软件中搭建工作电路。其中仿真工况转速为额定转速20000 r/min，导通相电流i=12 A。以A相为例，选取图3中point1处作为电磁力观测点，图4(a)和图4(b)即为BSRMWR径向电磁力及其FFT分析。

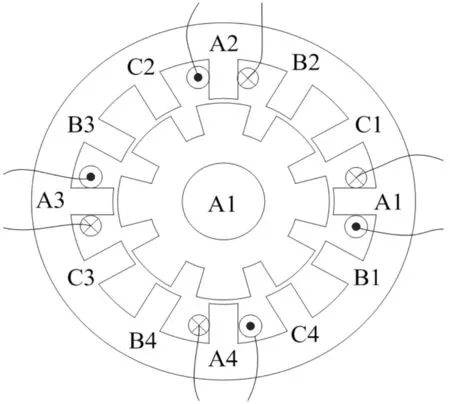
图1 12/8极BSRMWR结构示意图

图2 BSRMWR工作区间原理图

图3 BSRMWR电磁仿真模型

图4中BSRMWR直流分量为75 N，该直流分量并不会引起定子振动。在2666 Hz、5333 Hz、10666 Hz、13333 Hz、18666 Hz等频率处力波幅值相对较大，均可能引起定子较大的振动响应。

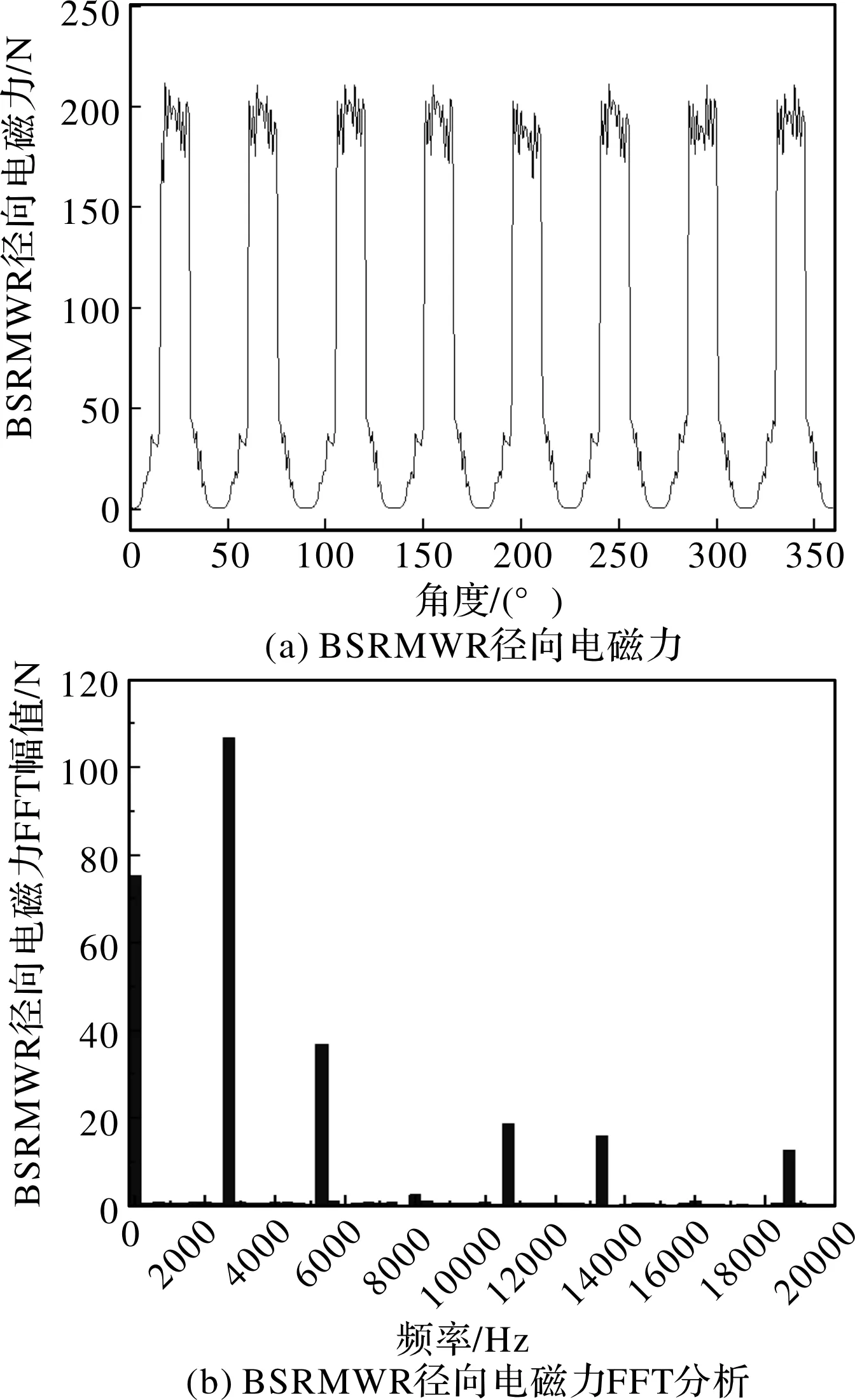
图4 BSRMWR径向电磁力及其FFT分析

3 BSRMWR的模态分析

图5为BSRMWR定子及其壳体模型在前处理软件ANSA下的网格模型，考虑到网格对计算精度的影响，这里设置网格尺寸为2 mm。

图5 ANSA网格模型

将网格模型导入振动噪声分析软件Virtual.lab，利用nastran求解器完成模态分析计算，设频率范围为人耳可听范围20 Hz～20 kHz，材料属性如表2所示。求解结果如图6所示。

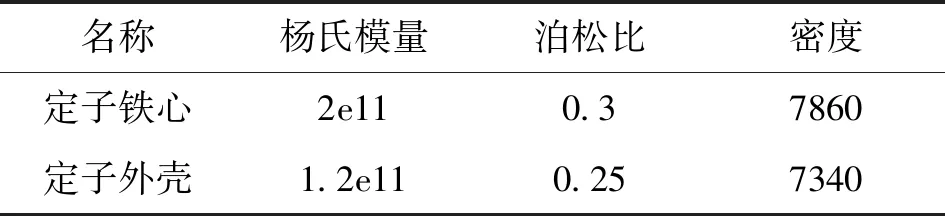
表2 材料属性

图6 BSRMWR模型模态分析

由图6可知，除了0阶模态振型(呼吸模态)以外，其他各阶模态均有两个非常接近的模态频率，这与电机模态分析相关理论一致[42-43]。研究表明：计算与分析电机定子固有频率及其模态对振动分析具有重要作用[44]。

4 BSRMWR振动响应分析

将JMAG中径向电磁力结果通过振动噪声分析软件Virtual.lab加载至电机定子齿作为振动响应的输入，如图7所示。根据图2所示BSRMWR的双相导通原理，转矩相和悬浮相的定子齿均受到径向电磁力作用。以图7所示为例，此时A相和B相工作，此时A1～A4为转矩相，B1～B2为悬浮相，即A相提供转矩，B相控制悬浮。

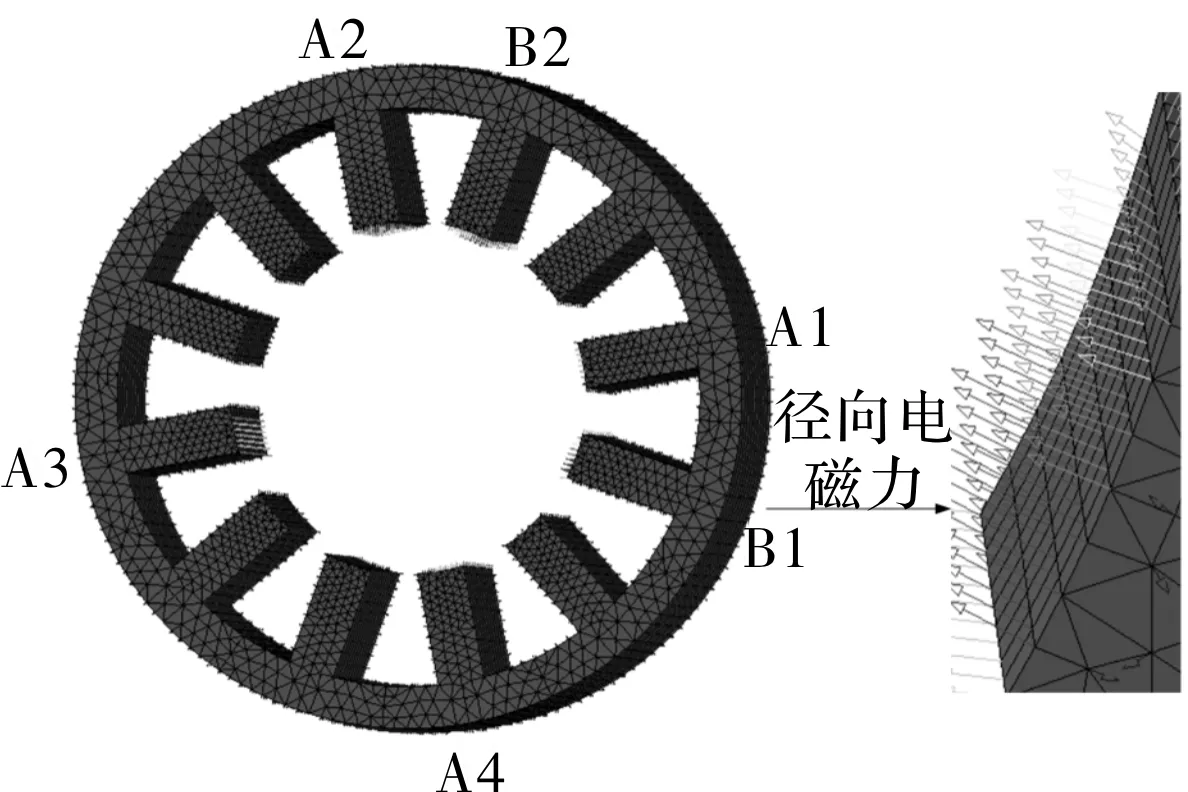
图7 BSRMWR不对称径向磁拉力

图8 BSRMWR振动位移响应云图

电机的振动噪声除了受电磁力的幅值、频率等影响，还与电机的共振状态有关。当BSRMWR径向电磁力的频率和定子模态频率相近时，也会产生较大的振动。因此，通过求解BSRMWR的模态频率为后续振动响应的分析做了铺垫。基于电机模态的频率分析，对BSRMWR进行振动位移响应分析，获得其振动位移响应结果，如图8所示。

由图8所示电机在2659 Hz、5318 Hz、10637 Hz和13296 Hz等频率处有较大振动响应。而径向电磁力幅值在2666 Hz、5333 Hz、10666 Hz和13333 Hz等频率处幅值较大。因此，当BSRMWR径向电磁力幅值较大时，对应的振动位移响应也较大。

为了研究各频率下电机振动位移响应的具体情况，在电机定子齿面和外壳上任意选择三个观测点，如图9所示。提取定子齿面和机壳零部件不同位置方向的位移响应，如图10所示。

图9 BSRMWR振动位移响应观测点分析

图10 BSRMWR振动位移响应

由图10分析可知：

(1)观测点3所处位置即BSRMWR定子齿面处，发现该处的振动位移响应最大，说明径向电磁力使定子齿发生了较大的形变；

(2)径向电磁力幅值在2666 Hz、5333 Hz、10666 Hz和13333 Hz等频率处较大，而振动位移响应在 2664 Hz、5330 Hz、10665 Hz、13305 Hz附近出现位移峰值，这说明径向电磁力较大时，振动响应也比较大。

(3)在8330 Hz、9656 Hz、14300 Hz附近出现振动位移响应峰值，这是因为径向电磁力的频率和电机的固有频率相近。当激振力与固有频率相近时会发生共振，振动加剧。

为了分析各阶模态在BSRMWR振动响应中的参与程度，通过计算模态参与因子即可得到各阶模态对主要峰值的贡献量。图11为BSRMWR振动响应下的前15阶模态参与因子幅值。

由图11可知，第1、2、5、6、8、11阶模态对电机振动的贡献比较大，故可针对这些阶模态进行优化。第8阶出现模态参与因子峰值是因为激励力的频率(9000 Hz)与结构的固有频率(9069 Hz)几乎相近，发生了较大的共振。

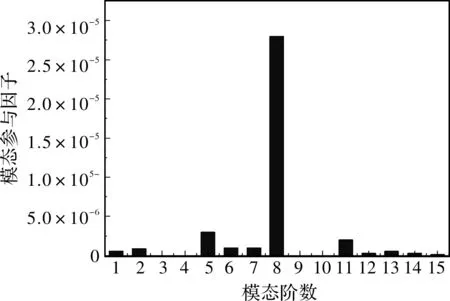
图11 BSRMWR振动响应模态参与因子

5 BSRMWR壳体结构优化

5.1 单向加强筋分析

由模态参与因子分析得出BSRMWR的第1、2、5、6、8、11阶模态对振动响应的贡献较大，本文基于模态参与因子通过添加加强筋以提高结构刚度。图12为加强筋示意图。图12给出了三种方式来添加加强筋，即沿着电机壳体轴向加筋和周向加筋(单向加筋)以及轴向和周向同时加筋(双向加筋)。

图12 加强筋示意图

鉴于篇幅有限，保持宽度和总用量不变，本节对比了不同厚度下单向加强筋周向和轴向两种情况。根据BSRMWR模型尺寸，如图13所示，模型1是BSRMWR外壳没有加强筋的计算模型，模型2是在模型1的基础上添加了轴向加强筋，主要是为了研究轴向加强筋对固有频率的影响。模型3是将模型2轴向加强筋改为周向加强筋模型，并保持加强筋的宽度W和总用量不变。

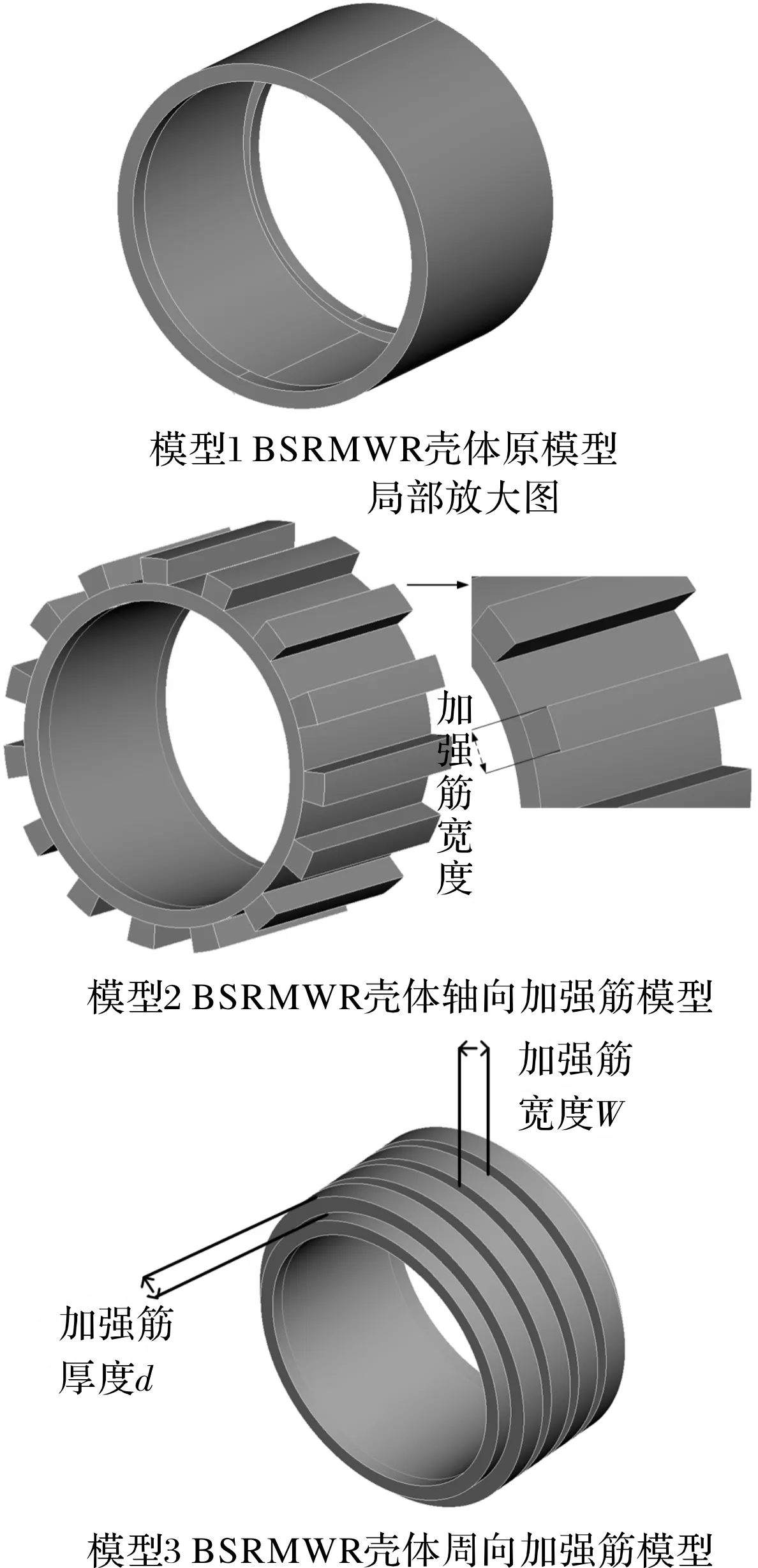
图13 BSRMWR壳体模型

由图11模态参与因子分析可知，第1、2、5、6、8、和11阶模态对振动响应的贡献较大。基于此，在单向加强筋均匀分布的条件下，对比了三种不同模型的模态频率，如表3所示。

表3 不同厚度加强筋模型模态频率

通过以上轴向加强筋壳体模型和周向加强筋壳体模型的对比，由表3可得如下结论：

(1)轴向加强筋壳体模型使电机的固有频率降低，而周向加强筋反之。因此，在利用加强筋对BSRMWR进行减振优选设计时，对加强筋结构的影响应当给予考虑。

(2)从降低电机振动的角度考虑，轴向加强筋模型弱化了电机结构，周向加筋模型使BSRMWR模态频率显著提高，故周向模型优于轴向模型，应当重点考虑电机壳体结构周向加强筋在电机减振方面的优势。

鉴于篇幅有限，为了研究加强筋厚度对模态频率的影响，保持加强筋的宽度和总用量不变，模型4和模型5分别是在模型2和模型3的基础上，改变了加强筋的厚度d。同时，随着加强筋厚度的增加或减小，根数也会相应地减小或增加。如表4和表5所示，分别表示模型4轴向和模型5周向不同厚度下的模态频率，其中厚度d1>d2>d3。

由表4和表5可知：在保持加强筋宽度和总用量不变时，考虑到第8阶模态对振动响应的贡献较大，轴向加强筋壳体模型会降低模态频率，这一结果在一定程度上虽然能抑制振动，但是同时也会弱化结构刚度，所以一般不予考虑。而周向加强筋对提高模态频率有显著作用，从结构刚度角度分析，模态频率提高有利于增强刚度。从减振角度考虑，周向加强筋壳体模型的效果会优于轴向加强筋壳体模型的效果。

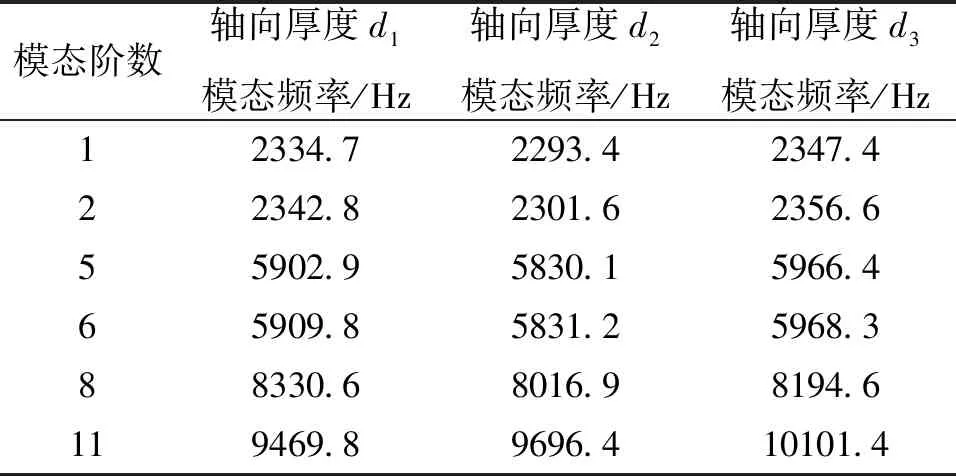
表4 不同厚度轴向加强筋模型模态频率

表5 不同厚度周向加强筋模型模态频率

5.2 双向加强筋分析

为了探究双向加强筋壳体优化结构对电机振动响应的影响，基于前文对单向加强筋的分析，这里将模型2轴向加强筋和模型3周向加强筋模型结合起来，得到图14所示双向加强筋壳体结构模型6。在保持宽度和总用量的情况下，分别分析轴向加筋模型、周向加筋模型以及二者结合的双向加筋模型对电机振动性能的影响。

由于结构的固有频率越低，越容易被外界激励源激励，所以在研究振动性能的时候，考虑更多的是低阶模态对振动的影响[39]，有效提高低阶模态频率对抑制振动有重要的参考意义。对比模型2轴向加筋模型和模型3周向加筋模型，以及二者结合的双向加筋模型6，分析得到第1、2、5、6、8、11阶的模态参与因子，如图15所示。由图15可知：通过给电机外壳添加合适的轴向加强筋或者周向加强筋均可以有效降低各阶的模态参与因子，从而各阶模态对振动响应的贡献度得到有效抑制。从效果上来看，发现双向加强筋的模态参与因子最低，这说明双向加强筋模型对振动的抑制效果更好。在抑制电机振动响应的时候，优选双向加筋模型最佳。

图14 BSRMWR壳体双向加强筋模型

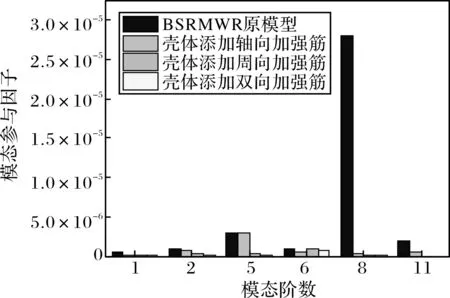
图15 BSRMWR振动响应优化前后模态参与因子

为了进一步说明BSRMWR不同的壳体模型对振动位移响应的抑制效果，这里提取了图9所示定子齿面观测点1处的振动数据，对比了轴向加强筋模型、周向加筋模型和二者结合的双向加筋模型下的振动位移响应，如图16所示。由于各低阶模态参与因子的得到了有效抑制，这说明各低阶模态减小了对振动响应的贡献度，而振动响应是各阶模态的叠加，因此由图16分析可知：优选的双向加强筋壳体模型对BSRMWR在减振方面有显著效果。

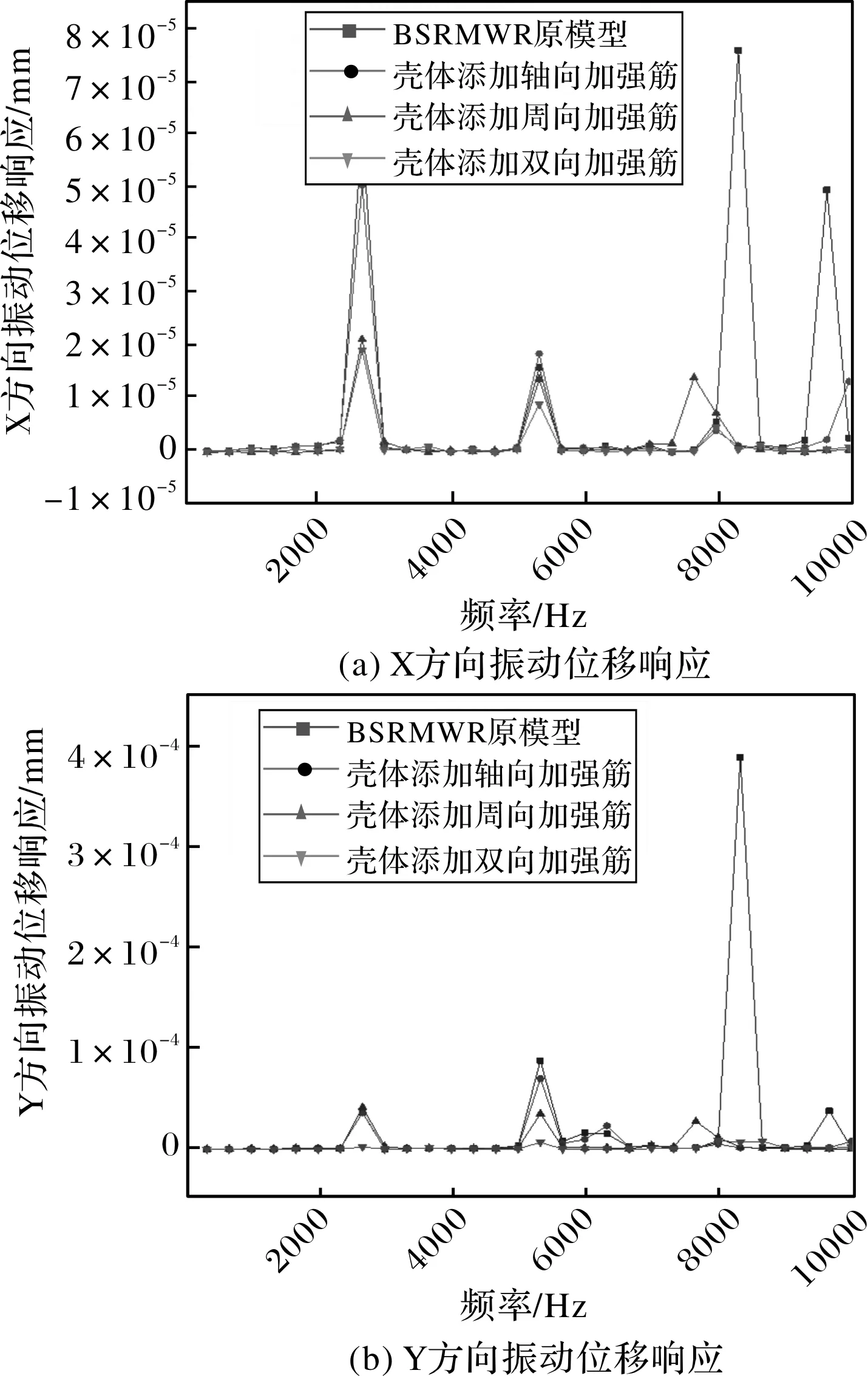
图16 BSRMWR壳体优化前后振动位移

6 结 语

本文分析了BSRMWR的振动响应，通过为电机壳体添加不同方向的加强筋来降低低阶模态对振动位移响应的贡献，从而改善电机的振动性能。得到如下结论：

(1)BSRMWR电磁力波幅值越大，振动响应幅值越大。

(2)当电磁力频率和结构固有频率比较接近时，即使电磁力幅值较小，但是由于共振，电机也会产生较大的振动。

(3)模态参与因子越小，则对应的模态阶数对电机振动的贡献越小。

(4)在加强筋用量一定的情况下，周向加强筋的效果优于轴向加强筋。若进一步将二者结合，则双向加筋模型效果更佳。