聚焦核心素养 考查关键能力——对2022 年苏州中考第8 题的解法探究

安徽省合肥一六八陶冲湖中学 武前炜（邮编：230012）

2022 年是“双减”政策实施后的首次中考，恰逢新课标颁布，各地中考试题备受关注.《义务教育数学课程标准（2022 年版）》指出：中考命题避免套路化，着重减少单纯考查技能熟练性的题目，保证学生有充足的作答时间. 立足核心素养是落实依据课程标准命题的一个重要维度. 逻辑推理是核心素养中最重要的思维品质，通过问题解答反映出学生个体智力或思维水平的差异性，包括深刻性、灵活性、独创性、批判性、敏捷性和系统性.好的试题不仅能客观的将学生在学习知识技能中形成的重要思维品质和关键能力反映出来，还可以体现出数学教育的价值，是学生获得良好数学教育的重要手段之一.2022 年苏州中考试题第8题是一道十分精致的优质考题. 本文通过多方位思考开拓学生解题思路，多角度转化目标，探究问题解决的方法，让思维“可见”，让解法“自然”.

1 试题呈现

（2022 年苏州中考第8 题）如图1，点A的坐标为( 0,2 )，点B是x轴正半轴上的一点，将线段AB按逆时针方向旋转60°得到线段AC. 若点C的坐标为(m,3 )，则m的值为（ ）

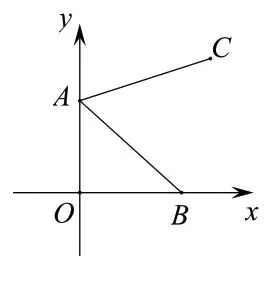
图1

图2

图3

2 图形分析

以旋转为背景，连接BC则可得等边△ABC，动点B在x轴正半轴运动，绕着定点A( 0,2 )旋转60°，容易知道点C的轨迹为射线. 依托等边△ABC可以构造一线三等角全等、等边三角形手拉手全等、辅助圆等等. 思维入口较多.

3 解法探究

思路1 一线三等角

根据∠CEF=∠CAB=∠BDE=60°,AC=AB，可知△CEA≌△ADB,

图4

图5

图6

思路2 抓住定点A( 0,2)

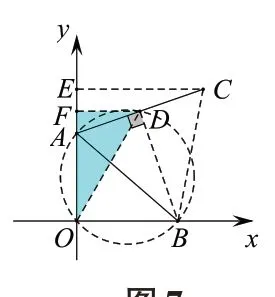
图7

图8

图9

思路3 隐圆转化

评析本解法抓住旋转问题的本质，静态图形联想动态过程，旋转变换遵循“集体行动，步调一致”，从而确定点C的运动轨迹. 实际上本题思维入口可以这么想，由于点B在x轴正半轴运动，那么当点B恰好处于特殊位置（原点O），尝试画出此时图形，点C的轨迹也就随之确定了. 如果继续思考，将△AOB整体旋转后图形即为图9 的△AC2C.

3 试题评价

本题属于几何综合题，图形简洁清晰，考生审题条件和问题清晰明了，展现命题者的人文关怀和命题温度. 在坐标系背景下，巧妙地将旋转和点的坐标结合在一起，结构简洁，数形结合，内涵丰富. 求点的坐标可以从两个方面思考，一是依托图形计算线段长，或者通过表达式. 要求学生具有较强的分解图形、整合条件、合理添加辅助线、构造基本图形的能力，解决方法具有多样性、灵活性. 考查学生直观想象的素养，分析问题的能力，综合运用学科知识分析问题和解决问题的能力，注重思维开放性、灵活性，重探究创新去模式固化，充分发展了学生的几何直观、推理能力、创新意识等初中数学核心素养.

4 教学启示

（1）问题驱使，培育能力

题海无涯，方法和策略是关键！“双减”政策要从从教师“增压”开始，教师要对数学知识有系统而全面的认识. 中考备考阶段，对于难点突破、效率提升、能力培养以及素养提升需要老师进行精心培育和指导，依托解题活动来训练数学思维，通过问题载体建立知识关联、形成良好的认知结构，积累数学活动经验、让学生形成数学思维，进而培养学生解决问题的能力.

（2）问题分析，发展素养

数学核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力及情感、态度与价值观的综合体现，这些是在数学学习和应用过程中逐步形成和发展的. 所以必要的探究活动和问题载体能为学生提供处理问题的思路与方法的平台. 探究过程中思维的点化、体验，是学生经验获取的重要途径. 本文从几何图形的结构入手，剖析旋转本质，建立旋转前后基本图形的特征以及彼此联系，理清了结构、看透了内涵、找准了突破口，最终形成解题经验. 告诫学生学习不能模仿、套用模型，要学会思考分析、形成解决问题的理性思维. 在分析和解决这一类问题过程中感悟转化思想，注重数学知识积累，逐步发展学生的数学运算、逻辑推理、抽象模型等数学核心素养.

（3）及时反思，提高效率

平时坚持解题后反思，怎么想？为什么这么想？这将对发展学生的几何直观大有裨益！教师在数学研究、学习、讲授中，不仅需要关注研究图形的方法、研究图形的结果，还需要感悟图形给我们带来的好处，几何直观就是在“数学——几何——图形”这样一个关系链中让我们体会到它所带来的最大好处. 日常教学中，对一些综合题进行一题多解、一图多思的分析与探究，能调动学生学习数学的积极性，促使学生在平时主动寻找、探究多种策略解决问题，及时反思积累，注重对通性通法的归纳总结. 所以，教师在中考备考中，重视几何图形的剖析，多视角分析综合题，帮助学生分析问题、构建模型、锻炼思维、形成经验积累，让数学思想和方法真正内化，这样能为学生在考场中赢得宝贵时间！