基于均匀设计法的三跨连续梁桥冲击系数多因素耦合

张 旭

（河南理工大学能源科学与工程学院，河南 焦作 454000）

1 引言

交通事业的大力发展，使得公路桥梁交通特征逐渐趋于高速化和重载化，不可避免地出现由路面不平度等因素诱发的车桥耦合振动，尤其当车桥共振过于激烈时，会大大降低车辆舒适性与桥梁结构的安全性[1]。冲击系数（IM）被认为是有效评价车桥耦合振动程度的重要指标，由于早期研究人员对车桥耦合振动认识局限性较大，很多国家主要通过试验获取实桥数据来探究车桥耦合动力特性，高效计算方法层出不穷，车辆模型及桥梁模型逐步精细化，车桥模型越发贴近实际运营状况，因此，高效的理论数值模拟方法成为解决车桥耦合问题的重要手段[2]。目前国内外多数学者利用基频或跨径来制定IM计算公式，我国2015年发布的《公路桥涵设计通用规范》（JTG D60-2015）通过归纳大量实桥数据，将IM 制定为基频的函数。但在实际场景中，公路交通状况发生较大变化，单一因素影响下的车桥响应并不能反映真实交通状态，因此，进行多因素耦合分析更具现实意义[3]。

谭国金等[4]为深入研究简支梁桥IM的影响因素，建立三维空间车型与桥梁模型，基于模态综合法，通过时程响应结果分析车辆行驶速度、车辆作用点及路面不平度等参数影响下的动力放大系数变化规律。邓露等[5]依据桥梁设计规范及大量调查数据拟定车辆模型基本参数，并与国内外车型参数作对比，通过建立4座简支梁桥模型，改变车辆总质量、车辆刚度、车辆阻尼等因素，分析车桥动力响应及IM变化规律，车桥动力响应研究结果表明，动力IM 受车辆总质量这一因素影响最大，呈负相关变化；与车辆刚度呈正相关变化；随车辆阻尼增大表现出先减小后增大的变化规律。朱荣芳等[6]通过建立钢管混凝土系杆拱桥的有限元模型，通过改变不同车辆荷载分析不同工况下IM 的变化规律，结果表明钢管混凝土系杆拱桥IM 随轴重增大而减小，与桥梁中线距离成反比，距离越大，IM越小；IM随车辆行驶速度先增大后减小，没有特定规律。项沛[7]以高敦大跨弯连续刚构桥为研究对象，改变车辆行驶方式、路面不平度、墩高等敏感因素，采用均匀设计法设计了20个工况，利用自编译车桥耦合程序，获得了最不利截面处各参数对IM的敏感程度及影响规律。

综上可知，已有车桥耦合研究主要针对简支梁，且多集中于单一或少量因素的影响研究，并未考虑路面不平度等其它重要因素作用。因此，本文开展多因素耦合下三跨连续梁桥冲击系数研究，以期为现行规范中冲击系数的制定提供参考。

2 冲击系数计算方法

车辆IM计算公式可表述为桥梁在车辆荷载激励下所产生的静态响应增量变化，见式（1）。

式中，Rdmax为汽车激励下桥梁竖向位移最大动力值，m；Rjmax为汽车激励下桥梁竖向位移最大静态响应，m。

中国桥梁设计规范中的IM 从1989 年开始规定为跨径的函数，而后通过研究初始条件各异的7 座桥梁，通过现场大量实桥数据采集，整理并进行回归分析得到基频的函数。公式（2）为《公路桥涵设计通用规范》（JTG D60-2015）中关于冲击系数的表达式。

3 均匀设计法

3.1 均匀试验设计原理

均匀设计原理是将数论和多元统计结合的一种方法，该方法通过选取试验范围内符合均衡分散特点的试验点，确保每一行每一列仅有一个试验点，力求进行最少的试验次数以获得较多的试验目标，与正交设计试验方法相比，试验次数明显减少，假设试验有5 个因素，这5个因素各有3个水平，如若进行全面试验，则需要5×3 种方法。因此，均匀设计特别适用于进行多因素多水平的未知试验[8-10]。

3.2 均匀设计表及试验步骤

均匀设计法的关键是设计均匀设计表，每一个均匀设计试验都有其对应的均匀设计表，即U*m（np），U*表示改进的均匀设计表，m 为试验次数，n 为水平数，p 为列数。

均匀设计主要步骤：①明确本次均匀试验效应及目标；②根据试验范围和试验条件，设置研究因素的合理范围及对应的水平数；③由公式（2）得出各因素范围及对应水平数后，确定U*m（np）的3 个参数；④根据均匀表确定试验方案，开始试验并采集相关数据；⑤将试验所得结果汇总，并利用回归分析方法将所得数据进行分析，达到试验目标。

3.3 回归分析

通过均匀设计法得到试验数据后，根据试验目标及试验性质等条件选择合适的方法进行回归分析。常见的回归方法有线性回归方法、非线性回归方法和二次回归方法等。本文主要采用线性回归方法，假设设计方案中共进行m次试验，随机变量Y与n个自变量X有线性联系，可得多元线性数学模型见式（3）。

式中，B0、B1...Bn为待定参数，ε1、ε2、...εm为m 个服从同一正态分布N（0，σ2）的随机变量。

逐步回归是利用最小二乘法原理并逐步引入各因素的多元线性方法，本质是在试验过程中，每引入一个因素即进行F检验，并对已选因素进行t检验，通过显著分析达到逐步消除影响较弱因素的目的。

4 多因素耦合下大跨连续梁桥冲击系数分析

4.1 工程背景

以国内某高速公路三跨连续箱梁桥为研究对象，桥梁全长220m，上部跨径布置为55m+110m+55m，桥面总宽12m，中间11m 为机动车道宽度，外侧为非机动车道，左右各0.5m护栏，横坡为3%，主梁截面形式为单箱单室，采用C50混凝土，汽车荷载为一级荷载。跨中、支点断面尺寸如图1所示。

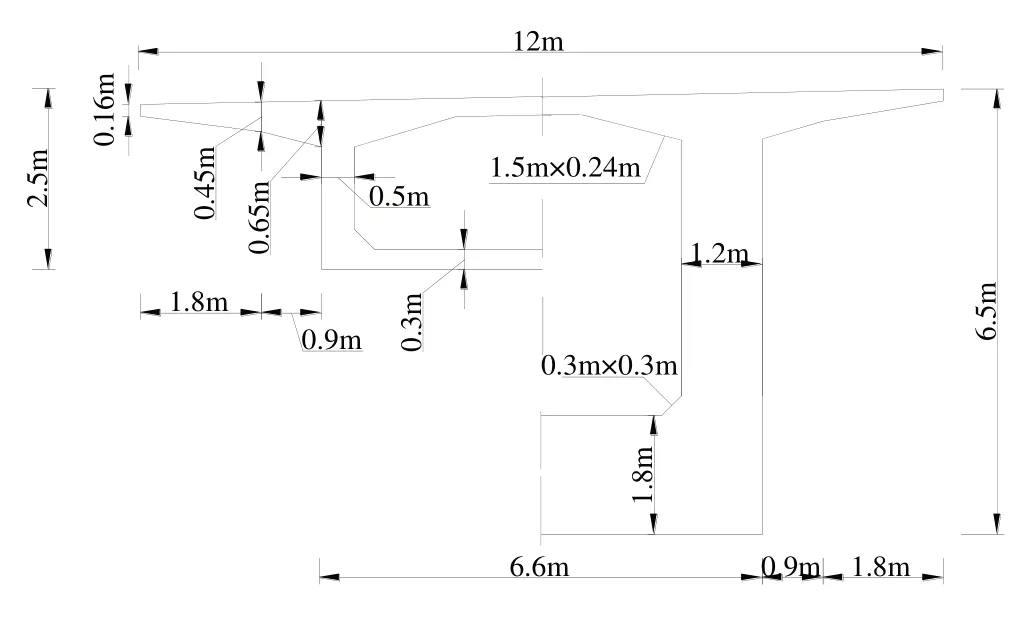
图1 变截面三跨连续梁横断面图

通过ANSYS 有限元软件建立仿真桥梁模型，采用beam188单元，该模型共划分80个单元，有限元模型如图2所示。

图2 三跨连续梁桥仿真示意图

对仿真模型进行模态分析得到节点、单元长度、角频率、阵型等，将模态数据正则化，可得桥梁模态方程：

4.2 车辆模型

选取文献[5]中的五轴重载拖挂车为研究对象，利用虚功原理，采用Largange 推导出车辆动力平衡方程。经分析可知有16个自由度：车头与车厢分别的浮沉、俯仰和侧翻自由度以及每个轴左右轮的10个浮沉自由度。该车辆模型各部件具体参数来自文献[5]，简图如图3所示。

图3 中m1v、m2v分别为车头、车厢质量；θ1、θ2、I1θ、I2θ分别为车体、车厢（纵向）转动角及俯仰转动惯量；φ1、φ2、I1φ、I2φ分别为车体、车厢（横向）扭转角及侧翻转动惯量；b 为左右轮间距；a1～a8为轴间距及质心间距；y1v、y2v分别为车头、车厢竖向位移；yiL、yiR分别为悬架竖向位移(第i 轴的左侧悬架与右侧悬架)；miL、miR分别为非簧载质量(第i轴的左侧质量与右侧质量)；diL、diR分别为车轮与桥梁接触处的竖向位移(第i 轴的左侧车轮与右侧车轮)；Kils、KiRs、Cils、CiRs分别为悬架刚度和阻尼(第i 轴的左侧悬架与右侧悬架)；Kilt、KiRt、Cilt、CiRt分别为轮胎刚度和阻尼（第i轴的左侧轮胎与右侧轮胎）。

图3 五轴重载车辆模型

依据动力学分析可知，任何车辆的平衡方程均可写为：

式中，MV为质量矩阵；CV为阻尼矩阵；KV为刚度矩阵；Fvb为相互作用力向量、yV分别代表加速度、速度和位移向量。

MV为15×15的方阵，矩阵形式见式（6）。

阻尼矩阵Cv、刚度矩阵KV同理可得，车桥耦合振动系统中相互作用力向量Fvb为：

4.3 桥面不平度

桥面不平度是影响车桥耦合分析结果的重要因素，因此在车桥耦合分析时不应忽略，本文采用谐波叠加法模拟桥面不平度，见式（8）。

式中，r（x）为所模拟的桥面不平度样本；m 为采样点数；Gd（ni）为位移功率谱函数；ni为第i 个区间的中心频率；Δn 为频率间距；x 为纵向位移；θi为随机相位角度，范围在[0，2π]内。

选取空间频率上限、下限分别为6m-1、0.01m-1，时间频率上限、下限分别为30HZ、0.5HZ，Gq（no）依据《公路桥涵设计通用规范》（JTG D60-2015）功率谱取平均值，取桥长220m，模拟A、B、C、D等级的桥面不平度如图4～图7所示。

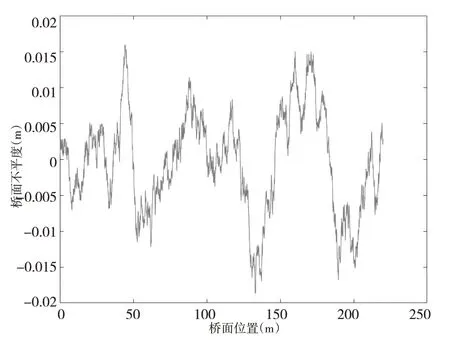
图4 A级桥面不平度样本

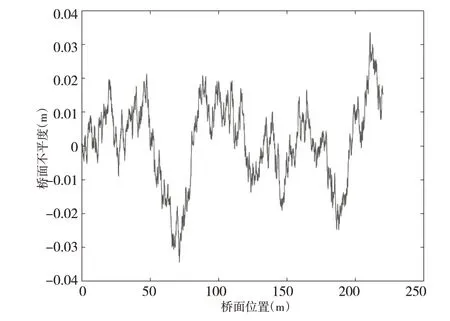
图5 B级桥面不平度样本

图6 C级桥面不平度样本

图7 D级桥面不平度样本

4.4 位移及力平衡建立车桥耦合方程

假设车轮与桥面始终接触，第i轴左车轮与桥梁之间的相对位移Δli、左车轮与桥梁接触位置处的相互作用力Fbv、Fvb可分别表示如下：

式中，Zli为左轮下缘对应的竖向位移；WLi为左轮接触处桥梁的竖向位移；rli为左轮接触位置处的桥面不平度竖向坐标；Kilt、Cilt为左轮的刚度系数和阻尼系数；dil为左轮与桥梁的相对位移。

5 基于拟水平均匀设计法的冲击系数分析

5.1 均匀设计试验方案

在车桥耦合分析中，影响IM 的因素多而复杂，且大多是讨论单因素变化的规律。本文考虑多因素耦合影响，利用均匀设计法减少试验次数，主要分析常见的几种影响因素并确定其水平数，具体见表1。

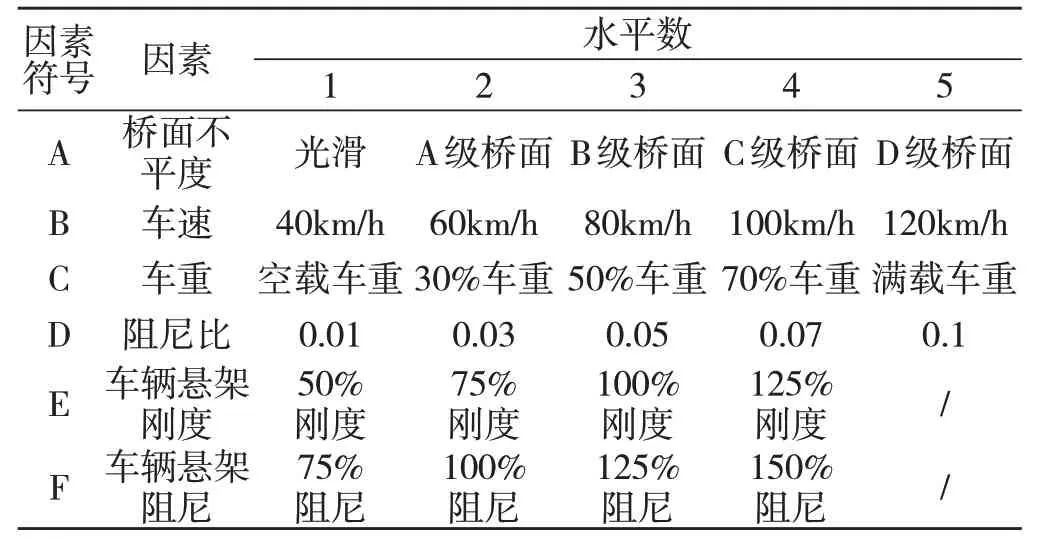
表1 各因素分析表

5.2 均匀设计表

A、B、C、D因素的水平数为5，E、F因素的水平数为4，所有因素水平数不一致。引入拟水平法可有效解决非一致水平数问题，该方法为达到试验目的而将某一因素的水平数按需求改变，改进后的均匀设计表及使用表见表2和表3。

表2 均匀设计表

表3 的的使使用用表表

表3 的的使使用用表表

分析表3 可知，本次试验因素6 个，即选取1、2、4、5、6、7 列设计表格，结果见表4。

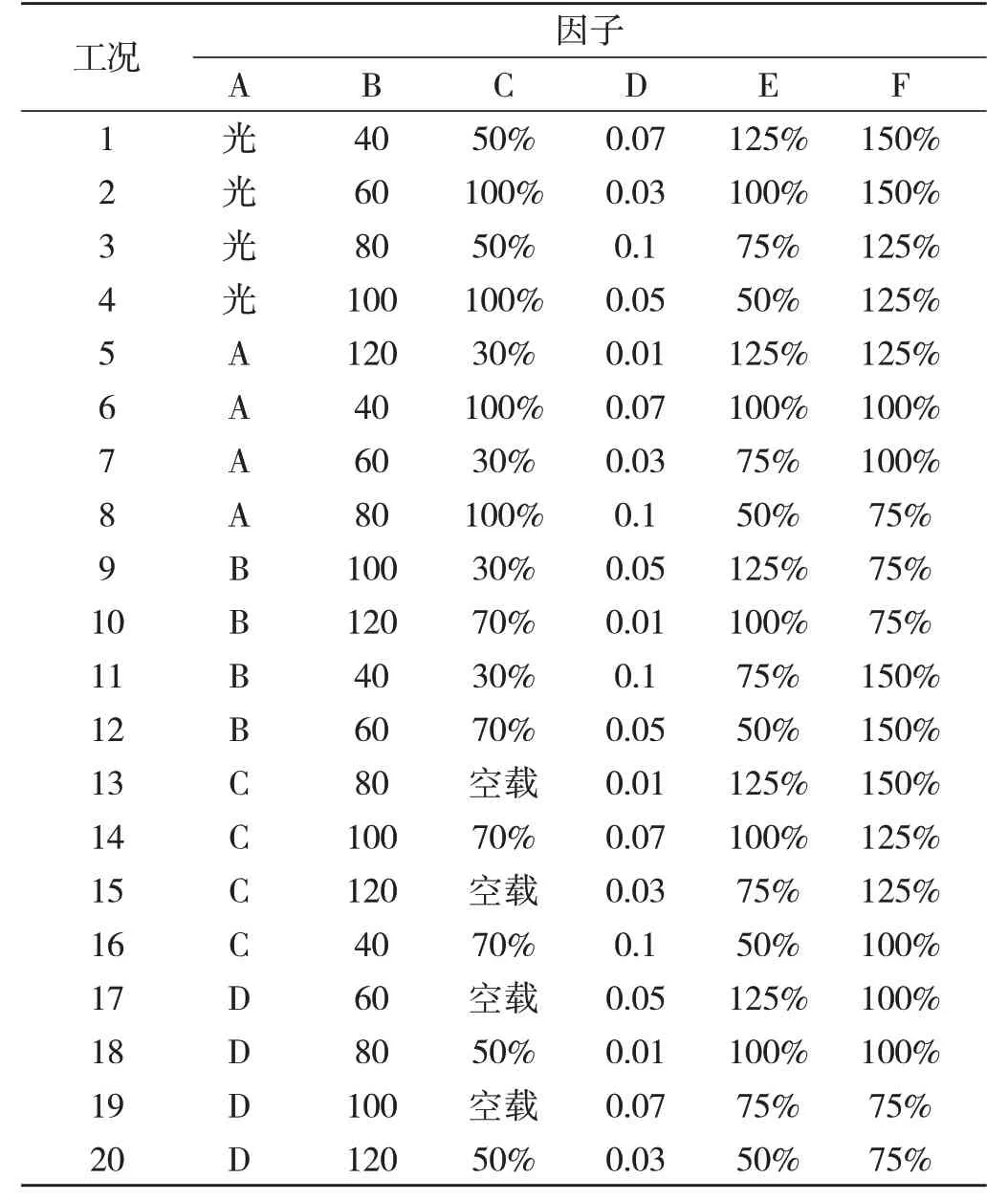
表4 工况设计表

试验方案确定工况后，利用自编车桥耦合程序对相应工况进行求解，得到关键截面的挠度IM、弯矩IM，计算结果见表5。

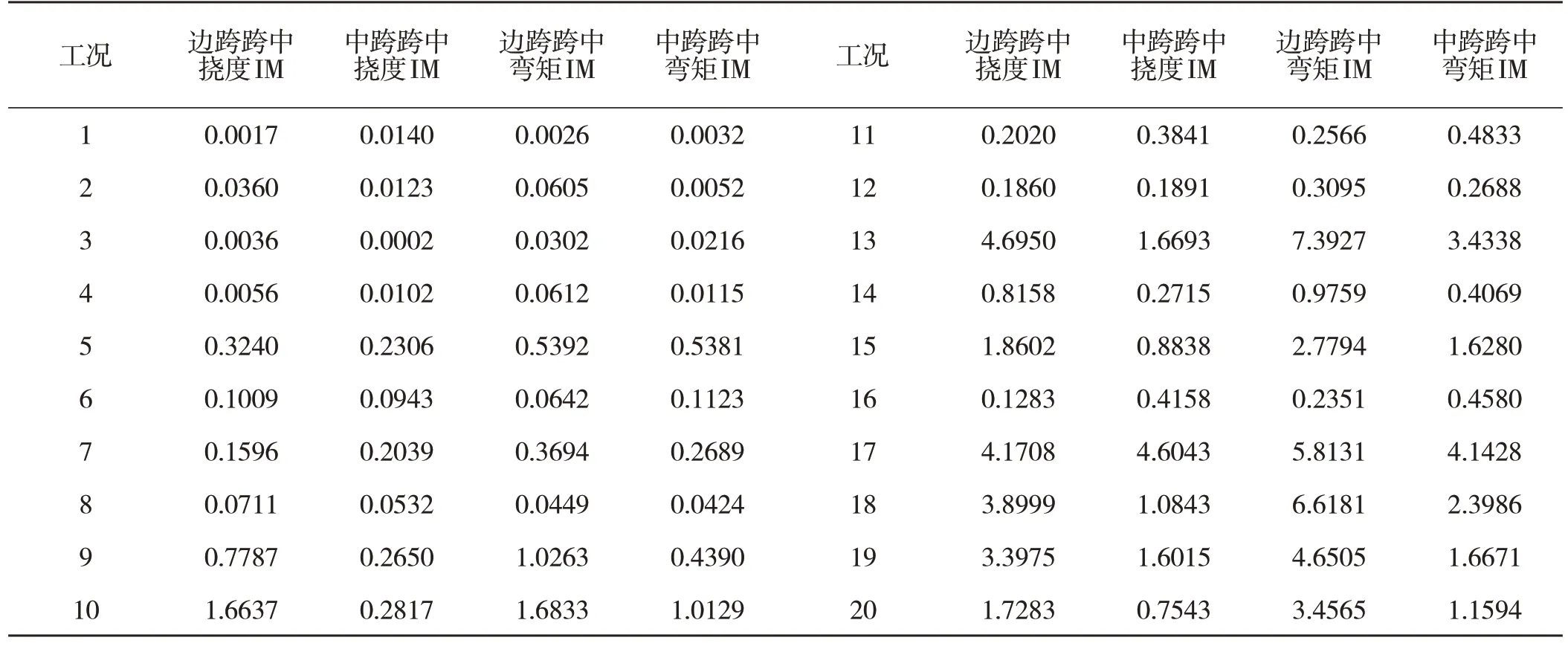
表5 截面冲击系数

通过SPSS分别对基于均匀设计法得到的数据表进行逐步回归分析，结果见表6。

分析表6可知，模型1中，取边跨跨中、中跨跨中两截面处的最大挠度IM 为因变量，Sig 小于0.05，此时受A、E两因素的影响较显著，相关系数R为0.847，相关性良好，可得挠度IM回归方程为：

表6 系数分析表

同理，模型2中，取边跨跨中、中跨跨中两截面处的最大弯矩IM 为因变量，Sig 小于0.05，此时受A、D 两因素的影响较显著，相关系数R为0.832，相关性良好，可得弯矩IM回归方程为：

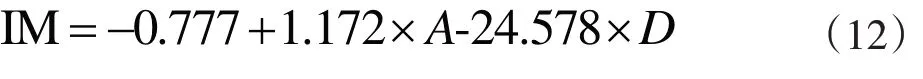
6 结语

①利用ANSYS 软件建立三跨连续梁桥模型，得到桥梁正则化模态方程，采用Largange推导五轴拖挂车动力平衡方程，依据车桥间的位移协调和相互力关系，并加入谐波叠加法模拟的桥面不平度，利用自编车桥耦合程序求解桥梁动力冲击系数。

②选取桥面不平度、车重、行车速度、阻尼比、车辆悬架刚度、车辆悬架阻尼作为主要考虑因素，为降低试验次数，引入均匀设计法，利用SPSS逐步回归得到挠度IM和弯矩IM的回归方程。

③挠度IM 和弯矩IM 的回归模型Sig 均小于0.05，相关系数分别为0.847、0.832，表明拟合公式良好，桥面不平度因素影响最大，因此，建议在相关桥梁IM 的制定中应考虑此因素。