数形结合思想在高中物理解题中的应用策略

孙　婷

数形结合思想在高中物理解题中的应用策略

孙婷

（江苏省江都中学，江苏扬州225200）

在高中物理教学过程中，随着数形结合思想的进一步深入，使得原本比较复杂的物理题目愈发简单、直接，在很大程度上缩短了学生的解题时间，并且也提高了学生的物理学习能力。基于此，本文对数形结合思想在高中物理解题中的应用情况进行了具体的分析。

数形结合思想；高中物理；解题

数形结合思想在高中物理解题过程中的应用主要是为了能够把具体的几何图形同数学方程式联系起来，使得具体问题能够得到一定程度上的简化，为学生解决相关问题提供便利。学生可以通过“数”分析“形”当中的问题，使得题目当中数量关系得到简化；也可以通过“形”分析“数”的本质，使得题目当中的抽象概念能够得到具化。

一、数形结合思想概述

数形结合思想指的是将数和形两者之间的关系有效地联系起来，以对题目当中的图形进行综合性的分析为前提，明确其中的数字表达式，使得物理问题能够得到解决。在高中物理解题过程中，应用数形结合思想能够对题目当中包含的数量关系有进一步的了解，也使得原本较复杂的题目能够得到简化，并且进一步提高学生的解题速度。将数形结合这种解题方式充分应用到物理教学过程中，能够给教师提供一种更加有效的教学方法和解题工具，使得一些物理难题能够得到更加有效地解决。

二、数形结合思想在高中物理解题中应用的重要性

高中物理是在初中物理的基础上对初中物理的一种延伸，无论是在高度上还是在深度上，都达到了一个全新的角度。高中物理可以将更多丰富多彩的物理理论和物理现象展示给学生，使得学生能够学到更加有深度的物理知识，并且对科学探究能够拥有更深的领悟，深刻感受到学习物理的魅力所在。不过，教师在对学生进行知识传授时，最重要的是应该教会学生学习方法和解题思路，并逐渐提升到形成物理思想的层面上，这样更加有利于学生未来的发展。物理作为一门自然基础学科，在学习过程中主要是需要学生能够通过所学知识解决物理问题和物理现象，并且逐渐参透事物的本质和内在关联。在学习如何运用所学的物理知识解决物理问题时，首先应该将物理思想培养起来，使得学生能够对所学的基本知识和基本方法有一个整体性的概括。与其他解题思路和解题方法比起来，学生的物理思想是基础，而解决物理问题的方法则只是一种外在的表现形式。因此，在学习物理知识和解决物理问题时，应该先学思想，然后再学方法。这样举一反三式的学习才能够提高学生的综合素质，促进学生的创新能力发展。

在高中物理教学过程中，应用数形结合思想一方面能够帮助学生从一个更加客观的角度认识现实世界，从而掌握解决物理问题的有效工具与方法，使得学生的物理思想能够得到进一步的丰富。在解决物理问题时应用数形结合思想，可以将物理的内在联系更加直观地表现出来，然后从一个更加直观的角度解决实际问题。目前，将数形结合思想应用到高中物理教学过程中，将数形结合思想作为学生解决物理问题时一个必备的基本思想是非常有必要的。通过数形结合思想将原本深奥复杂的物理难题以更加直观、形象的方式表示出来，给学生提供了更加简单、直接的解题方法，并且可以让学生从一个更加直观的视角认识客观世界，把原本比较复杂的问题逐渐简单化，原本比较抽象的问题逐渐具体化，这样更加有助于帮助学生从更深层次的角度理解事物之间的联系，并且抓住事物的本质特点。

三、数形结合思想在高中物理解题中应用的特点

数形结合思想就是把物体的空间形式和数量关系结合起来，通过数与形之间的对应和转化解决问题的思想。其实质就是把抽象的数学语言、数量关系和直观的图形结合起来。往往能将复杂的问题简单化、抽象的问题概括化，帮助学生找到快捷的解决思路和方法。

首先，运用抽象化的方式认识事物，并对其特征以及一些其他相关问题加以理解，然后运用数形结合思想对事物进行处理。例如，在《电磁学》当中，如果想解决粒子运动的相关问题，那么就需要将粒子或者是对象看作是一个质点。其次，在对相关对象的问题进行讨论时，一般都会应用符号化方法，运用一定的符号语言，以此将事物对象的性质、关系，以及特征通过形式化的方式演算出来。最后，在对具体对象进行研究时，应该将一定的模型建立起来，运用抽象的方式将思维与认识对象之间的数量关系和空间关系以各种图像的形式呈现出来。

（一）高中物理教材与数形结合思想的结合

在高中物理教材当中，其内容与数形结合思想有着非常密切的关联性，基本上每一个章节的内容都可以运用数形结合思想，并且数形结合思想在物理教材当中也有不同形式的体现。一般情况下可以将高中物理教材与数形结合思想的结合形式分成三类：第一类，按照表达对象之间的差异，可以划分成表达式、原理图、流程图、实物图以及示意图；第二类，按照数学知识的应用情况，可以划分成方程和不等式、几何图和向量以及平面函数；第三类，按照不同的呈现方式与应用方式，可以划分成图表语言、符号语言以及模型语言。

（二）运用符号和公式对物理概念与规律进行简化

如果需要对物理学内容加以表示，那么符号语言是其中非常重要的一种方式。在世界上，所有的事物基本上都是具有两面性的，一方面体现在质上，另一方面体现在量上。物理学的基本概念与规律都是在研究质的过程当中形成的，而物理学公式则是在研究量的过程中，对符号语言进行了进一步的浓缩。同时，如果想要探究事物的本质，那么一定要对事物的量进行重点研究，从而更加全面地掌握事物的客观规律。一般情况下，都会使用文字对物理学当中的规律与概念进行表述。这对于高中阶段的学生而言是具有一定难度的，因此需要综合运用一些简单的方式，以此帮助学生进行消化和理解，这时应用符号和公式就是非常适宜的。将物理现象以符号或者是公式的形式体现出来，一方面能够将物理概念与规律以更加简洁、准确的方式呈现出来；另一方面也可以使学生的思维过程得到全面的提高。运用公式将原本晦涩难懂的文字概念表述出来，使得各个物理变量之间的关系能够以更加清晰、直观的形式展现在学生眼前，更加有利于帮助学生消化和理解物理知识概念。

四、数形结合思想在高中物理解题中的实际应用

在高中物理解题过程中，应用数形结合思想主要是把数和形结合起来，以此将数和形的优势充分体现出来，使得原本比较深奥的物理问题能够得到简化，把各种不同的图形转变为可以帮助学生更好地理解的数学表达式，使得学生能够有更加清晰、直观的思路解决物理问题。在应用数形结合思想的过程中，有四种比较常见的解题思路。

（一）形的数化

在解决物理问题时，有非常多的物理题目都是运用图形方式表达出来的，而在解决物理问题时，一定会应用到非常多的物理公式。基于这样的情况，因为物理题目当中的图形往往比较抽象，这就使得学生没有办法第一时间找到解决问题最正确同时也是最精准的表达式，使得学生解题时间大大增加。这时就需要应用形的数化思路，把原本抽象的图形以数学表达式的方式呈现出来。学生在阅读完题目以后，只要能够准确地找出应该使用哪一个具体的数学表达式，就可以对物理题目当中的数形关系进行更加准确地分析与理解，使得学生的解题效率能够得到显著的提升。实际上，在对高考物理试卷进行研究分析时可以发现，有非常多的题目都可以运用数形结合的方式进行解决，而在应用过程中应该注意结合题目当中的图形将数学表达式准确定位出来，然后进行更加细致分析，使得题目能够得到快速并且正确地解答。

例如，如图1所示，A1和A2是两个竖直放置的平行挡板，A1和A2之间的距离是6L。在A1和A2之间存在两个匀强磁场区域，分别是Ⅰ和Ⅱ，但是其方向是反向的，把MN当作是水平面上的理想分界面。应用BO表示Ⅰ区域的磁感应强度，在垂直方向纸面朝向外部，A1和A2分别正对着小孔S1和S2，两个小孔和分界面MN之间的距离是相等的，都是L。在宽度是d的匀强电场上，两个质量分别是m和＋q的例子，从静止到加速以后，沿着水平方向从S1进入到了Ⅰ区域，同时又直接向MN上的P点进行了偏转，而后才进入到Ⅱ区域。P点和A1板之间的距离是L的k倍，在不计算也不考虑重力以及碰到挡板的粒子的情况下，（1）如果k的取值是1，那么匀强电场的电场强度是E，应该如何应用关系式进行表示；（2）如果2＜k＜3，那么在水平方向上的粒子会从S2当中射出，此时在磁场当中粒子的速度v和k之间的关系，以及Ⅱ区域内磁感应强度B和k之间的关系，分别用关系式应该如何表示。

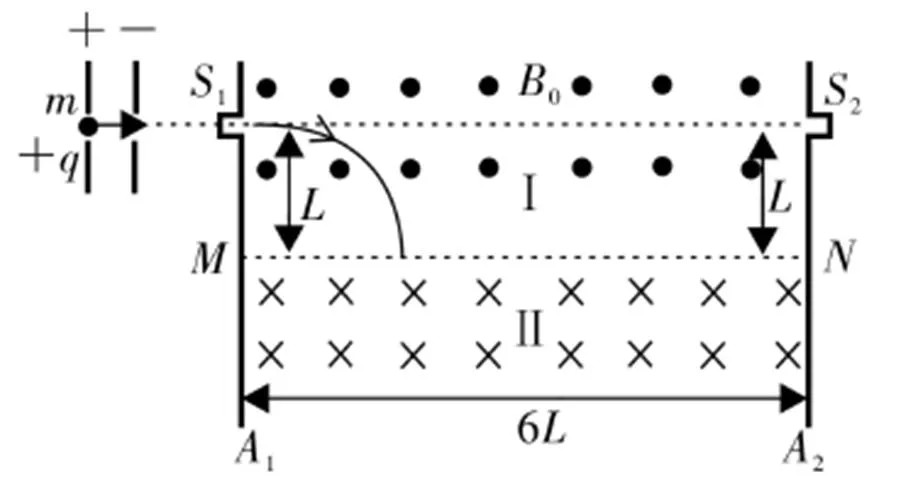
图1

在解决上述物理问题时，首先教师应该将正确的数学表达式表示出来，然后结合学生学过的物理知识，在电场当中运用动能定理将数学表达式列出来：

上海市水资源管理系统以水资源实时监测的建设和完善为基础，以水资源“三条红线”管理应用为核心，以支撑最严格水资源管理制度的实施和考核为目标，其基本要求是：实时掌握全市规模以上取用水户取用水情况、动态掌握重要水功能区及重要城市饮用水水源地水质达标情况；动态掌握全市水资源及其开发利用的基本信息；在线监督全市取水许可、水资源论证、水资源费征收、计划用水等水资源管理制度的执行情况；开展水资源调配，逐步增强对水资源配置工程和重要取水口实行体系化控制的能力；动态掌握突发性供水安全事件及应急处置情况，对重大突发事件进行应急反应和及时处置。

（1）Eqd=1/2mv2

在这个表达式当中，主要表示了粒子在Ⅰ区域当中的洛伦兹力，而其提供的向心力应该表示为：

当k的取值是1时，几何关系R=L，综合上式可以得到：

（2）当2＜k＜3时，通过阅读题目可以知道，在Ⅱ区域当中，粒子只发生了一次偏转，通过几何关系可以得到：

（x-1）2＋（KL）2=R2

在Ⅱ区域当中，粒子的洛伦磁力提供向心力：

通过对称性和几何关系可以得出：

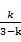
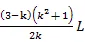
以此按照题意找到最准确的数学表达式，然后按照步骤对数学表达式进行计算，使得物理题目能够得到快速准确地解答。

（二）数的形化

在物理教材当中，无论是哪一个章节，都会涵盖比较多的物理公式，并且在实际解决物理问题时，常常会应用到这些物理公式。特别是在一些比较特殊的情况下，因为物理题目当中蕴含的数量关系比较复杂，使得学生必须要在实际做答时应用非常多的物理公式，学生解决物理问题消耗的时间大大提高。这时就需要应用数的形化思想，以此运用图形表示那些复杂性比较高的数量关系，从而进一步分析并深入理解题目当中蕴含的不同数量关系，进而提高学生解决物理问题的效率。

（三）以数解形

为了使物理问题能够被更加直观地描述出来，一般都会使用图像对问题信息加以表述。图像本身既存在好的一面，同时也存在不好的一面。好的一面在于表现形式直观且形象，而不好的一面在于准确程度不够高。在对物理问题进行处理时，应该逐渐强化学生分析与理解图像的能力，使得学生能够在图像当中找到有用的信息，明确图像和物理变量之间潜在的关联，并且在分析过程中找到其中蕴含的物理规律，并进行合理的转换，以解决相应的物理问题。

（四）以形助数

以形助数主要指的是通过图形解决物理问题，也就是在观察和处理图形的过程中，使得物理概念能够更加具体，使其转化成图形语言，从而使复杂的问题能够得到简化。在解决物理问题的过程中，有一些物理问题是存在已知量和未知量的，但是两者之间的关系却很难得到明确，所以需要依靠图像帮助学生进行分析，从而得到具体的关系方程。另外，在应用代数运算解决一些实际问题时，有一些问题很难得到有效的解答，这时就需要对这类问题实施转化，最便捷的方式就是依靠图形。应用数学语言、文字语言以及物理语言等方式，对物理相关概念和规律以及具体的现象加以解释，可以使问题的难度得到一定程度上的简化，更加有利于学生理解并做答。

五、结语

综上所述，在解决物理问题时，结合实际情况应用数形结合思想，更加有利于解决一些复杂并且抽象的问题，能够使学生更快、更好地掌握解题思路与方法，从而懂得如何寻找正确的解题方向，快速解决物理问题。在实际教学过程中，教师应该强化对学生数形结合思想的培养，使得数形结合思想能够成为学生学习物理知识、解决物理问题的一个重要途径。

[1] 李涤非.数形结合思想方法在高中物理教学中的应用研究[D].苏州大学,2015.

G632

A

1002-7661(2022)29-0070-03