超声速火箭橇流动特征和气动力激励振动分析
余元元, 王方元, 王彬, 孙建红,, 许常悦, 孙智
(1.南京航空航天大学 飞行器环境控制与生命保障工业与信息化部重点实验室, 江苏 南京 210016;2.南京航空航天大学 民航应急科学与技术重点实验室, 江苏 南京 211106)
在各种先进技术的推动下,超声速和高超声速飞行器设计受到了国内外研究机构的重点关注。例如,美国国防部21世纪初开始实施的NHFRP计划,以及2019年发布的“高超声速应用研究国家联盟”项目[1]。开展高速飞行器设计研究需要开展大量的试验以验证新的理论与技术。对于飞行器的空气动力学试验而言,常见的试验方式有风洞试验、真实飞行试验和地面滑行试验等。由于受到空间限制,风洞仅能开展缩比尺寸高速飞行器试验。真实尺寸高速飞行器的空中飞行试验成本较高,不适合在设计阶段开展。
火箭橇试验系统属于一种地面滑行试验装备。它以火箭发动机为动力装置,推动装有被试件的试验平台沿着高精度轨道高速滑行[2]。火箭橇试验系统兼具风洞试验和自由飞行试验的优点。与风洞试验相比,火箭橇试验系统可以开展全尺寸试验而非缩比模型,获取的试验数据更加真实可信。目前学者对于风洞流场品质的改善和试验精度的提高已有过大量研究[3-5],而对于提高火箭橇试验精度的研究较少。相比于自由飞行试验,火箭橇试验系统的整体研制周期更短,试验效费比更高。因此,火箭橇试验系统具备较好的实用价值和发展前景,可应用于机载设备的性能试验、空气动力学试验等研究。
美国是最早开展超声速火箭橇研究并着手建设的国家,设计并建造了二十多条用于火箭橇试验的轨道。其中,最为著名的轨道为霍洛曼高速测试轨道[6]。美国以此为依托进行了多项试验,积累了大量的数据,研究人员也针对这些数据提出了许多火箭橇系统理论。俄罗斯、英国及法国都相继建成了自己的火箭橇试验系统,主要用于弹射与导弹试验[7]。
我国火箭橇试验系统发展较晚,直至1997年才于湖北省建成第一条火箭橇滑轨。随着我国襄北高精度火箭橇滑轨扩建工程的开展,滑轨长度已达六千余米,足以开展超声速火箭橇试验[8]。然而,大量的试验数据表明,随着运行速度的增加,火箭橇在滑轨上产生的不利振动会逐步加剧。该试验场上的多次失败试验结果表明,这种不利振动会威胁到火箭橇试验的安全[9]。火箭橇的振动来源主要涉及橇/轨接触、火箭发动机推力波动以及高速运动带来的气动力致振。其中,气动力致振是指火箭橇头激波与地面、轨道与扣件发生碰撞反射,对橇体产生非线性的气动力激励振动。反射激波与边界层相互作用会形成新的涡流[10],在一定程度上破坏理想试验环境。此外,相较于旋成体部分,滑靴、支撑件等类方柱体结构会发生更为明显的振动响应[11]。
针对火箭橇的气动力问题,国内外学者已经开展了一些相关的试验和数值研究工作。Krupovage等[12]对3种双轨超声速火箭橇进行了多次试验,发现气动力是造成拉力改变的重要原因。Rigali等[13]开展了单轨超声速火箭橇试验,结果表明火箭橇地面试验可以较好地还原低空飞行器的飞行环境。Zhang等[14-16]分析了火箭橇的数值边界条件,并采用结构有限元方法对某型双轨火箭橇进行数值模拟,计算结果与试验结果吻合较好。张立乾等[17]对超声速单轨火箭橇运行过程中的气动变化进行了数值模拟,发现气动力的非恒定性、火箭发动机所产生推力的偏心度都会引起橇身的振动。党峰等[18]对某火箭橇一体化设计结构进行数值模拟,并讨论了跨声速工况时气动外形对流场特性的影响。Lofthouse等[19]利用CFD软件对霍洛曼高速测试轨道的窄轨火箭橇在空气和氦气环境下进行三维数值模拟。结果表明,垂直楔形滑橇产生的激波会冲击到火箭橇体,激波产生的高温高压停滞区域会降低火箭橇性能,甚至会损坏火箭橇滑行试验。Lumb等[20]设计了一种新的火箭橇试验,并利用CFD进行效果测试。通过对运行轨道进行预热,可以把火箭橇运行速度由Ma3提高到Ma5。Strike等[21]对位于固定在轨道上的火箭橇进行了来流Ma为2至5的风洞试验,并改变了离地高度、滚转角等参数,获得了滑块距离、来流马赫数等参数对火箭橇气动载荷的影响。
由于超声速火箭橇常采用尖拱旋成体构型,橇体头锥处形成的斜激波与地面、轨道和轨道扣件发生复杂的碰撞、反射以及相互作用。为了深入认识这些激波结构的特征及产生的气动力影响,有必要逐步剥离反射物体(地面、轨道及其扣件)的影响,进而探索气动力致振的机理。基于这些研究,可以为超声速火箭橇的气动减振设计提供理论依据,这就是本文的研究目的。
1 数值计算方法
1.1 控制方程组
超声速火箭橇的滑行过程属于可压缩湍流问题。因此,超声速火箭橇流场的控制方程为三维可压缩Navier-Stokes方程。在笛卡尔坐标系中,包含连续性方程、动量方程和能量守恒方程的控制方程组可以写作如下守恒形式:

式中:Sij=0.5(∂ui/∂xj+∂uj/∂xi)为应变率张量;T为静温;γ为空气比热比;μ为空气的分子动力学黏性系数,可根据Sutherland公式求出;μT为湍流黏性系数;Pr为层流Prandtl数;PrT为湍流Prandtl数,常近似取定值0.92。
1.2 湍流模型
湍流黏性系数μT需要通过建模求解。本文采用基于SST两方程湍流模型的尺度自适应模拟(SAS)方法[22]开展湍流计算。在SST两方程湍流模型中,湍流黏性系数μT可通过求解湍动能k和涡量密度ω的输运方程得到
湍流黏性系数μT可以通过(10)式求出

(10)
输运方程中的各种参数详见文献[23]。为了实现SAS计算,需要在涡量密度方程(9)中添加SAS源项QSAS
(11)
式中:ζ2=3.51,σφ=2/3,C=2,κ=0.41;L为与湍流长度尺度
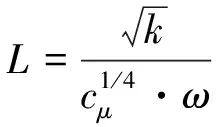
(12)
卡门长度尺度按(13)式计算
(13)
式中:Δ=(ΔxΔyΔz)1/3,CS=0.11。
1.3 计算方法
火箭橇沿着轨道的滑行过程为单一方向的滑行,故可通过指定运动函数的动网格方法对火箭橇的运行过程进行模拟。为了规定网格变形的范围,需要在绘制计算域网格时指定运动部分。本文采用基于铺层算法的动网格技术[23]对火箭橇的滑行过程进行模拟。作者前期的研究表明基于SAS方法的动网格技术可以用于超声速火箭橇滑行流场的模拟[24]。
控制方程组(1)~(3)采用基于结构网格的有限体积方法进行求解。为了捕捉超声速火箭橇流场中的激波等强间断结构,采用二阶精度的Roe通量差分裂格式对黏性项和对流项进行离散。为了保证时间的二阶精度,时间推进采用子迭代技术,单个时间步长内进行20次迭代计算。在当前模拟中,火箭橇流场中的固壁设置为无滑移无穿透的绝热壁,地面、轨道及轨道扣件处的固壁设置为滑移壁。其他边界处设置压力远场边界条件。
1.4 计算物理模型
鉴于超声速绕流存在头激波的特点,为了减少头激波引起的波阻,现有的超声速火箭橇常采用尖拱旋成体构型。本文研究的超声速火箭橇安装在单轨上,橇体采用尖拱旋成体构型,如图1a)所示。为简化计算,数值模拟采用的火箭橇计算物理模型仅保留火箭橇试验平台的橇体、轨道及轨道扣件,去除下方的支撑结构及车身,如图1b)所示。火箭橇橇体长度为2 170 mm,直径为280 mm。轨道扣件长宽高分别为160,150和150 mm,沿轨道周期性安装在地面,相邻扣件间距为1 250 mm。火箭橇中轴线距离地面高度为563 mm。火箭橇流场数值模拟采用长方体计算域,计算域长、宽、高分别为28 328,4 500和4 000 mm。

图1 超声速火箭橇的物理模型图
在超声速火箭橇滑行过程中,旋成体构型的橇体头锥处会形成附体激波。为了对比分析激波结构特征,本文还对2种特殊工况进行研究:①超声速火箭橇橇体的无限空间内绕流;②仅包含地面的超声速火箭橇橇体绕流。在第一种工况中,长方体计算域长、宽、高分别为41 239,26 320和26 880 mm;在第二种工况中,火箭橇中轴线距离地面高度也为563 mm,长方体计算域的长、宽、高分别为41 239,26 320和13 583 mm。
2 计算结果分析与讨论
2.1 计算细节
为了便于讨论分析,对研究的对象分别做如下标记:火箭橇橇体在不受限环境下的超声速绕流记为“Case1”;火箭橇橇体在仅包含地面环境下的超声速绕流记为“Case2”;带轨道及轨道扣件的超声速火箭橇滑行过程记为“Case3”。
3种研究对象模拟均采用结构网格,并且沿壁面法向对边界层内的网格进行局部加密。Case1网格总数约为880万;Case2网格总数约为770万;在Case3中,由于采用基于铺层算法的动网格技术模拟火箭橇的滑行过程,故针对运动区域和静止区域分别构建结构网格。其中,运动区域网格总数约为170万,静止区域网格总数约为1 100万。火箭橇壁面法向第一层网格间距的Δr+值约为O(10),满足SAS方法中的近壁RANS计算要求。其中,Δr+表示利用黏性壁面单位规则化的壁面法向网格间距。所有模拟的时间步长均取定值5×10-6s,环境温度取300 K,来流(滑行)马赫数均取为2,来流(滑行)攻角均为零。此外,为了考察滑行速度对超声速火箭橇气动特征的影响,还对研究对象Case3模拟Ma2.5和Ma3运行速度下的火箭橇滑行过程。Case1的总迭代计算时间为0.05 s,Case2的总迭代计算时间为0.05 s,Case3的总迭代计算时间为0.04 s。
2.2 地面效应对超声速火箭橇气动特征的影响
当超声速气流掠过尖拱旋成体时,会在其头部形成附体弓形斜激波[25]。激波属于一种强间断面,气流在激波面前后的气体参数会发生突然变化,满足Rankine-Hugoniot关系。当火箭橇橇体处于不受限的超声速气流环境时,橇体的超声速流场几乎呈现对称特征,橇体头锥处的斜激波结构向远方传播直至耗散,橇体尾部会形成膨胀波,如图2a)所示。当仅存在地面影响时,激波会在橇体下方发生规则反射,如图2b所示。经过地面反射后的激波传播至橇体下表面,发生激波/湍流边界层相互作用,进而导致橇体表面局部压力上升。由于耗散效应的存在,反射至橇体的激波经过二次碰撞后强度明显减弱。对于超声速火箭橇而言,向下传播的头激波会与轨道、轨道扣件以及地面发生碰撞。由于轨道扣件按照等间距方式安装在火箭橇地面轨道两侧,故高速运动的头激波会周期性地掠过轨道扣件,发生周期性碰撞。对比头激波未作用于轨道扣件时刻和作用于轨道扣件时刻(如图2c)~2d)所示),火箭橇橇体下壁面的压力分布类似,这说明头激波掠过轨道扣件时未产生反射至橇体的激波。然而,当头激波与地面碰撞反射时,也会产生作用于橇体的反射激波。此外,当头激波掠过轨道扣件时,会在轨道扣件后方产生局部高压区。

图2 火箭橇对称截面上的瞬时静压分布
为了定量分析地面效应对火箭橇表面压力分布的影响,图3给出了沿着火箭橇上下表面中心子午线上的压力系数Cp曲线。
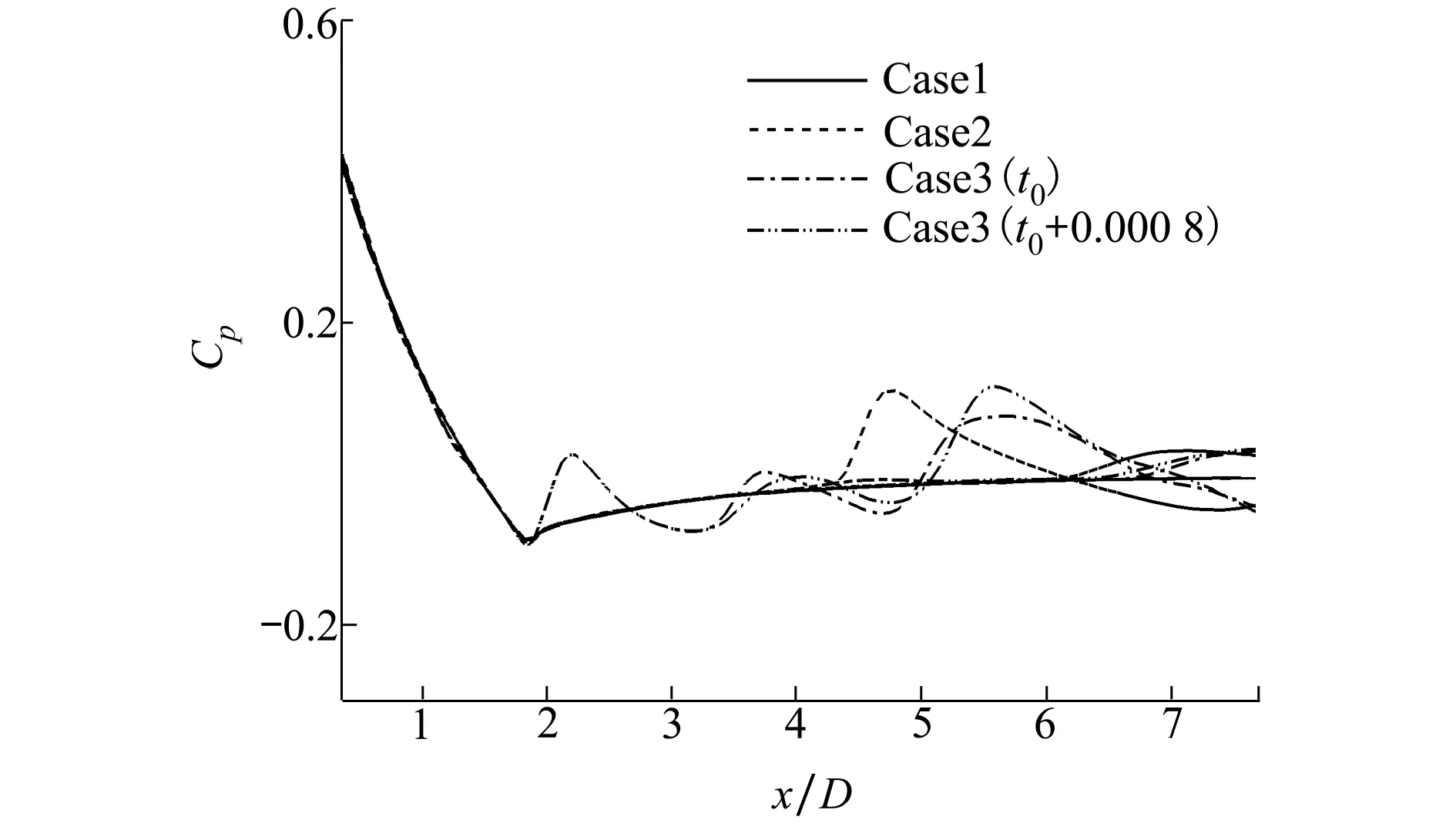
图3 沿火箭橇上下表面中心子午线上的瞬时压力系数分布
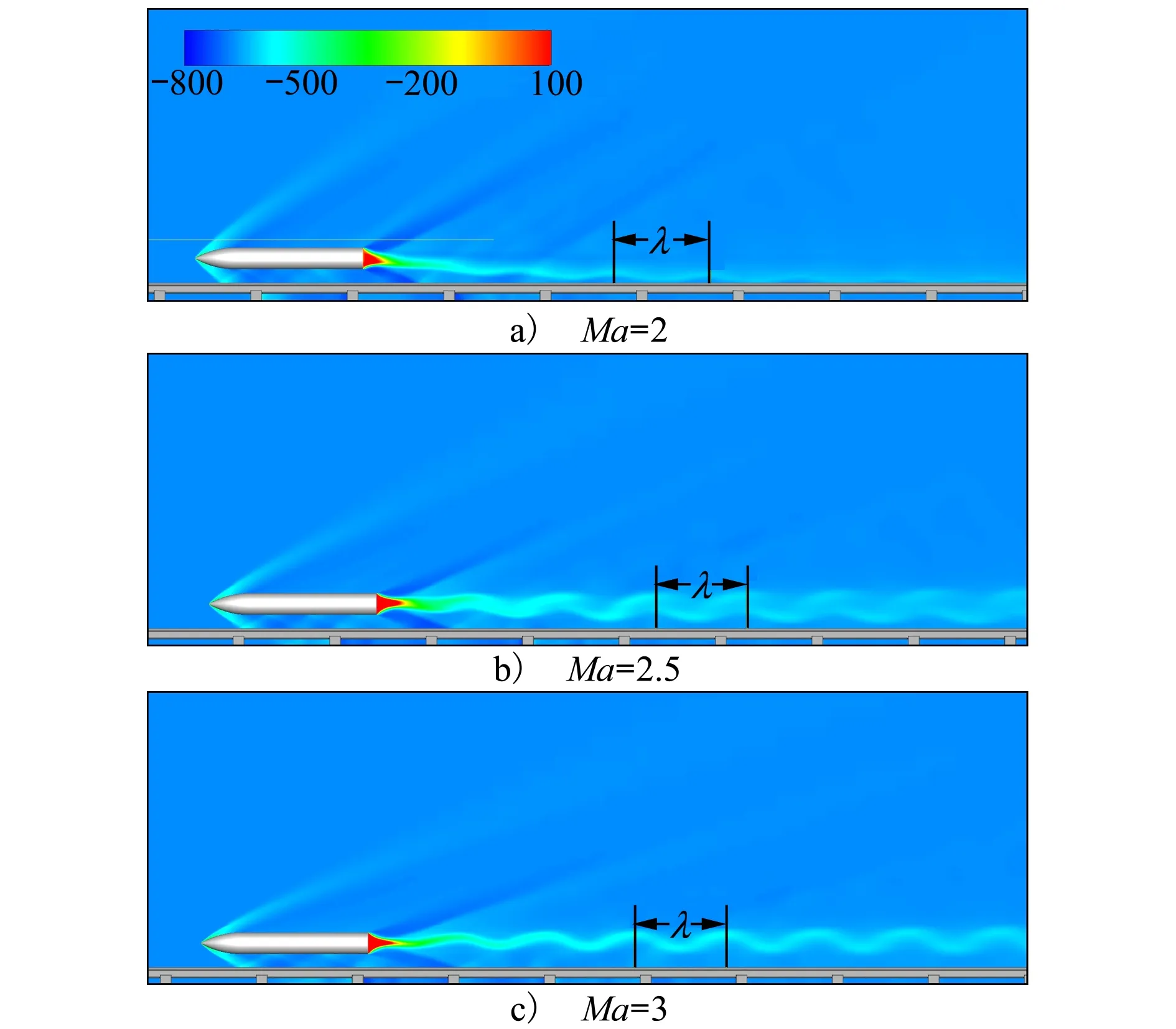
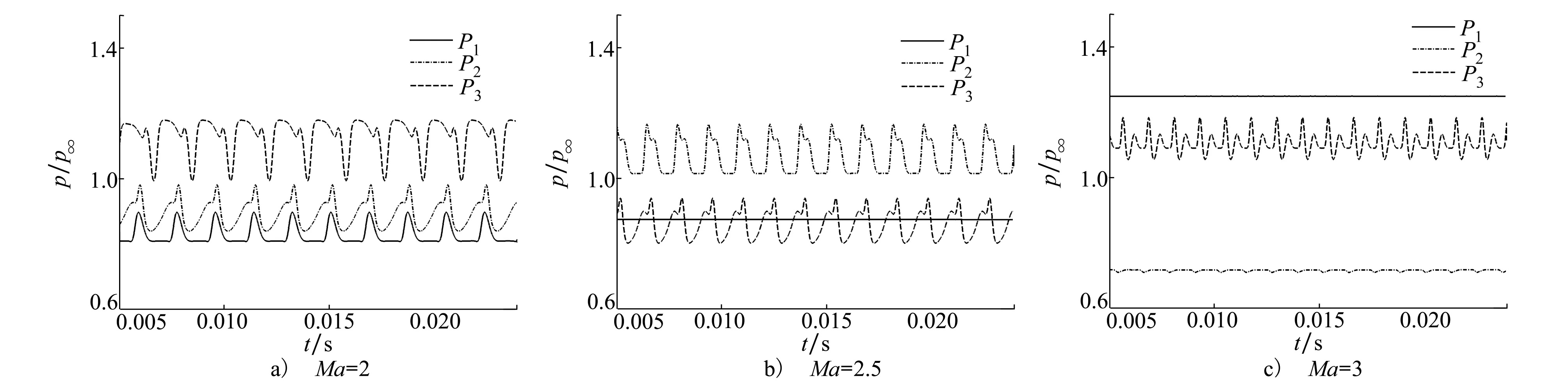
由于头激波的存在,火箭橇头锥处的压力明显高于其他区域。当火箭橇橇体处于不受限环境时,头锥后方的橇体表面压力系数分布较为均匀,这与橇体表面流动未受到周围环境影响有关。当仅存在地面的影响时,头激波经过地面反射作用于x≈4.1D附近的橇体表面,反射激波使得该处的Cp值明显抬升。当地面安装有轨道及轨道扣件时,轨道碰撞反射的激波使得x≈2.2D附近的Cp值得到抬升,地面反射的激波使得x≈5.7D附近的Cp值也得到抬升。需要特别注意的是,在2.2D 反射激波在橇体表面作用的位置并非单独的点,而是沿着橇体表面的一个曲线。因此,橇体下表面的局部压力波动势必导致橇体升力的变化。表1给出了不同工况下的超声速火箭橇受力特征。 表1 超声速火箭橇的平均受力特性 可以看出,反射激波的存在使得火箭橇产生升力,这将加剧火箭橇试验平台车身与轨道接触引起的振动。此外,反射至橇体的激波还会导致火箭橇阻力略微上升。图4给出了橇体下表面的瞬时摩擦阻力系数Cf分布。Cf的定义为 (14) (15) 式中:τw为壁面摩擦应力;n代表橇体表面法向;ρ∞为环境空气密度;U∞为火箭橇来流(滑行)速度。从图4中可以看出,3个橇体的头锥处Cf值明显高于其他位置。根据Rankine-Hugoniot关系不难得知,这与头锥位于头激波波后有关。在Case2和Case3中,如图4b)~4d)所示,由于反射激波与橇体湍流边界层发生相互作用,在橇体下表面形成弧形作用区域。与Case1相比,这些弧形作用区域处的Cf值略有下降,而作用区域下游的Cf值则明显上升。Zuo等[27]也发现了类似的现象。从整体而言,反射激波对橇体产生的气动力激励会使得橇体的表面摩擦阻力增大,这与表1得出的阻力变化趋势一致。 图4 火箭橇下表面上的瞬时摩擦因数分布 激波与湍流边界层相互作用在影响壁面摩擦因数的同时,也对近壁处的涡量生成产生影响。壁面涡通量(ωBVF)可以反映壁面的涡动力学特征[28]。ωBVF的定义为 (16) 当雷诺数较高时,ωBVF可近似改写成 (17) 公式(16)和(17)中:ω为伪涡矢量,n表示壁面法向矢量。从公式(17)中可以看出,ωBVF可以反映壁面的双重动力学影响[29]:一是外部流场对壁面的胀压效应;二是壁面的剪切效应,也即近壁附近涡量产生的机制。 图5给出了火箭橇下表面的瞬时壁面涡通量幅值分布。在3种工况中,橇体头锥处均有明显散布的|ωBVF|峰值,这与橇体头激波的胀压影响有关。在Case1工况中,橇体头锥下游的|ωBVF|值几乎为零;在Case2工况中,地面反射激波对橇体中部产生胀压影响,进而导致该位置处出现|ωBVF|峰值;在Case3工况中,橇体上出现多处|ωBVF|峰值,这与头激波与轨道、轨道扣件以及地面发生碰撞产生复杂的反射激波有关。此外,头激波与轨道扣件碰撞对橇体表面的ωBVF值分布影响较弱,这进一步印证了头激波与轨道扣件碰撞后产生的扰动波属于强度较弱的压缩波。由此可见,反射激波与橇体的湍流边界层发生相互作用是橇体近壁处涡量产生的重要原因。需要注意的是,激波的胀压效应对跨越激波的涡量变化影响可以忽略,激波引起的涡量增加则与流体拉伸效应有关[30]。这进一步验证了ωBVF反映的上述动力学影响机制,即剪切效应是涡量产生的重要原因。 图5 火箭橇下表面上的瞬时壁面涡通量幅值分布 在火箭助推下,火箭橇通过加速实现超声速滑行。由于火箭助推器推力并非完全均匀,火箭橇的超声速滑行过程属于变加速过程。为了对比认识滑行速度对超声速火箭橇流动特性的影响,把超声速火箭橇的变加速滑行过程简化为不同滑行速度下的匀速运动。图6给出了不同滑行马赫数下的超声速火箭橇速度场分布。 图6 不同滑行马赫数下的超声速火箭橇速度场 可以看出,超声速火箭橇的尾迹存在明显的非定常特征,这与反射激波诱导橇体表面的涡量生成有关。随着滑行马赫数的增加,火箭橇头锥处的弓形斜激波激波角变小。当Ma=2时,火箭橇的尾迹向地面偏斜。然而,随着Ma的增加,火箭橇的尾迹向上抬升,且呈现明显的上下周期摆动。经过分析可知火箭橇尾迹的周期摆动波长λ约等于轨道扣件间距。不难得知,这些扰动波的传播速度与火箭橇的滑行速度一致。因此,这些扰动波的传播频率fw可以通过(18)式进行计算 (18) 式中,U∞为超声速火箭橇滑行速度。当火箭橇的滑行马赫数分别为2,2.5和3时,这些尾迹扰动波的波动频率分别为554,680和816 Hz。 与列车轨道类似,火箭橇的轨道扣件也是等间距安装在地面上。当超声速火箭橇滑行时,头激波会周期性地掠过轨道扣件,头激波碰撞到轨道、轨道扣件以及地面时均会产生反射激波。这些反射激波作用在橇体的位置会发生周期性变化,对橇体产生周期性的气动力激励,进而导致火箭橇产生振动。 为了获取火箭橇气动力激励振动的特征频率,在火箭橇橇体下表面设置了3个探测点,如图4d)所示。图7给出了这几个探测点处的压力信号曲线。 图7 火箭橇下表面上的压力信号 图中,p∞为环境压力。当Ma=2时,3个探测点处的压力信号存在明显的周期性波动;当Ma=2.5时,P1探测点处的压力信号几乎不存在波动,这意味着此时P1点位于反射激波作用区域上游;当Ma=3时,P2点处的压力信号也几乎不存在波动,这说明反射激波作用的区域随着滑行速度的增加而向下游继续移动。由此可见,滑行速度增大,头部激波强度增大,激波角度减小,相应的反射激波角也减小,其影响区域后移,影响区域的压力波动频率变高,波动值变化范围减小。 图8 压力信号的功率谱密度分析 反射激波对火箭橇橇体产生的气动力激励振动可以通过对压力信号作功率谱密度(PSD)分析得出。图8为不同滑行马赫数下3个压力信号的PSD分析曲线,曲线峰值对应的Strouhal数(Sr)即为气动力激励振动的特征频率。Sr的定义为 (19) 式中:f为频率。从图8中可以看出,Ma=2,2.5和3时的特征Strouhal数分别为0.224,0.220和0.225(对应的频率分别为554,680和816 Hz)。当滑行马赫数为2时,襄北试验场的实测气动力激励振动Sr数为0.22,这表明当前计算结果具有较好的可信性。由上文分析可以知道,气动力激励振动的频率与尾迹扰动波的波动频率一致,这意味着火箭橇气动力振动对尾迹波动具有锁频现象。这种锁频现象也常见于振翅射流射流和圆柱周期振荡流[31-32]。此外,PSD曲线中还可以看出,反射激波引起的火箭橇气动力激励振动存在倍频关系,这说明气动力振动存在谐声现象,这在Lamb的超声速火箭橇试验中得到了印证[33]。振翅射流和圆柱周期振荡流中的锁频现象也往往在功率谱曲线上出现倍频关系[31-32]。因此,有理由认为气动力振动的谐声现象与气动力振动对尾迹波动的锁频现象密切相关。 本文采用基于铺层算法的动网格技术对超声速火箭橇的高速滑行过程进行数值模拟。为了深入认识地面效应对超声速火箭橇气动特性的影响,对比分析了橇体在不受限环境和仅存在地面效应下的超声速绕流。当前工作还对不同滑行速度下的火箭橇流场拓扑特征以及气动力激励振动进行了研究。通过对计算结果的分析与讨论,有如下结论: 1) 超声速火箭橇的头激波传播至轨道和地面时发生激波反射,头激波与轨道扣件发生碰撞产生强度较弱的压缩波,导致火箭橇表面压力出现不同幅度的振荡。 2) 反射激波的存在使得超声速火箭橇产生升力,且阻力略有增加。升力的产生将进一步加剧火箭橇车体与轨道之间的碰撞振动。此外,反射激波使得橇体表面的涡量增加,进而使得其尾迹区流动呈现非定常波动。 3) 反射激波对超声速火箭橇产生气动力激励振动。通过对压力信号的功率谱分析可知,该振动的频率和尾迹的波动频率一致,即气动力振动对尾迹波动具有锁频现象。此外,功率谱密度分析表明气动力激励振动存在倍频关系,这说明气动力激励振动存在与锁频现象密切相关的谐声现象。
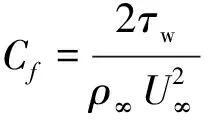
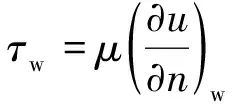


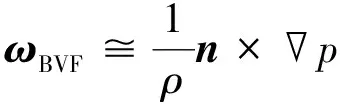

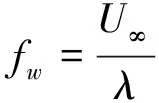
2.3 超声速火箭橇的气动力激励振动

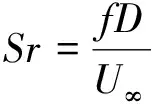
3 结 论

