基于Kalman滤波的改进灰色模型在基坑变形监测中的应用

刘国超，彭卫平，朱晓强

(1.广州市城市规划勘测设计研究院，广东 广州 510060； 2.广东省城市感知与监测预警企业重点实验室，广东 广州 510060)

1 引 言

随着城市化进程的快速推进，大城市人口规模的快速增加，使得城市土地愈发紧张，建筑设计向上要空间，使得楼层越来越高，基坑越挖越深，建筑规模越来越大，随之而来的工程沉降、工程塌陷问题愈发突出。高层建筑一般位于城市核心地带，基坑规模大，周边环境复杂，施工引起的沉降问题不容忽视，如果发生险情可能引发投资增加、工程安全或人员伤亡等一系列问题。基坑监测作为验证基坑设计、保护基坑施工的主要手段，可以直观反映基坑在各种施工工况、岩土体卸荷载状态下的变化情况，通过对监测数据的分析和预测，可以为后续设计和施工提供有益指导[1]。

基坑监测数据由于其离散性、高噪声等特点，使得监测数据呈现一定的波动性、随机性，为了对基坑的稳定状态及变形趋势做出更加准确的分析，国内外学者做了很多有益尝试。文献2中介绍了新陈代谢GM(1，1)模型在建筑物沉降数据预测中的应用，相比于传统的GM(1，1)模型和多项式拟合模型，精度提高明显[2]；文献3中建立了基于卡尔曼滤波的灰色理论预测模型，利用迭代滤波理论和LevenbergMarquardt优化滤波，有效提高了预测精度[3]；文献4中系统阐述了自适应卡尔曼滤波在变形监测数据处理中的应用，并探讨了不同自适应卡尔曼滤波模型的不同应用领域[4]；文献5中详细讨论了离散线性系统的卡尔曼滤波模型建立及精度评定，并将其应用于大坝动态变形监测中[5]。以上探索和尝试，为变形监测分析和预测提供了丰富工具，本文拟采用Kalman滤波+新陈代谢GM(1，1)模型组合方式，利用Kalman滤波对原始监测数据滤波消噪，并结合新陈代谢GM(1，1)模型对变形趋势项进行建模分析，来预测变形趋势。结合实际案例分析，基于Kalman滤波的新陈代谢GM(1，1)相比于传统的单一GM(1，1)、ARMA模型[6-7]，有效降低了观测噪声影响，并具有更高的预测精度。

2 基于Kalman滤波的新陈代谢GM(1，1)模型

2.1 Kalman滤波模型

Kalman滤波是一种利用线性系统状态方程，对系统状态进行最优估计的一种算法，能有效剔除测量数据中随机扰动误差，得到接近真实情况的测量数据。其数学模型包括状态方程(也称动态方程)和观测方程两部分：

Xk=Φk/k-1Xk-1+Wk-1

(1)

Lk=HkXk+Vk

(2)

式中，Xk是tk时刻系统的状态向量；Lk为tk时刻系统的观测向量；Φk/k-1为时间tk-1至tk的系统状态转移矩阵；Wk-1为tk-1时刻的动态噪声；Hk为tk时刻的观测矩阵；Vk为tk时刻的观测噪声。

离散的线性系统Kalman滤波递推公式为：

状态预报：

(3)

状态协方差阵预报：

Pk/k-1=Φk/k-1Pk-1+Qk-1

(4)

状态估计：

(5)

状态协方差阵估计：

Pk=(I-KkHk)Pk/k-1(6)

其中，Kk为滤波增益矩阵，其具体形式为

(7)

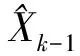
2.2 GM(1，1)模型

灰色模型是通过少量的、不完全的信息，建立数学模型并做出预测的一种方法，是黑箱概念的推广，通过分析系统各因素之间是否具有确定关系来区别白色与黑色系统，进而建立数学模型，并做出预测。

设观测原始序列：

x(0)={x(0)(1)，x(0)(2)，x(0)(3)，…，x(0)(N)}

对x(0)作一次累加生成(1-AGO)，得到：

(8)

从而获得生成序列：

x(1)={x(1)(1)，x(1)(2)，x(1)(3)，…，x(1)(N)}

设x(1)满足：

(9)

其中，常数u称为发展灰数，a为内生控制灰数，是对系统的常定输入。通过最小二乘估计可得：

(10)

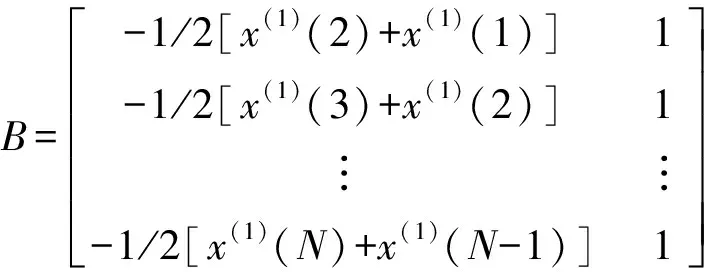
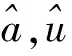
(11)

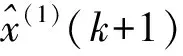
2.3 Kalman滤波与GM(1，1)模型组合及算法实现

Kalman滤波能有效剔除测量数据的随机项，得到接近真实情况的测量数据；新陈代谢GM(1，1)模型可以对监测数据趋势项进行建模，以预测变形趋势。本文拟采用Kalman滤波+新陈代谢GM(1，1)模型组合方式，利用Kalman滤波对原始监测数据滤波消噪，并结合新陈代谢GM(1，1)模型对变形趋势项进行建模分析，来预测变形趋势。

首先采用Kalman滤波对监测数据进行滤波，剔除监测数据中的随机扰动误差，然后对剔除了随机项的监测数据进行GM(1，1)建模。针对灰色系统随时间推移，预测精度与可靠度不断下降的问题，本文拟通过将已经获取的最新已知信息引入模型，淘汰作用弱的信息，淡化灰平面的灰度，以降低模型精度的损失，准确反映系统状态。

图1 基于Kalman滤波的改进灰色模型算法流程

3 算例分析

广州城区某高层建筑，基坑周长约 600 m，开挖深度 16 m，基坑等级为一级。为监测基坑施工过程中的变形情况及周边影响，在基坑及周边建筑布设若干监测点，本文选取基坑桩顶某竖向位移监测点14期数据作为实验数据，通过前10期数据建立模型，预测后4期数据，并与实际监测数据对比，其中每期监测间隔为7天，监测数据如表1所示。

表1 某监测点部分沉降数据

这里选取前4个数据为观测值，定△t=1，组成法方程进行动态平差，采用线性拟合y=a0+a1x+ε，得到状态协方差阵和状态估计参数。利用上面的递推预报与滤波公式可得到监测点的滤波值，如表2所示：

由表2可知，卡尔曼滤波通过建立状态方程和观测方程来描述系统的动态过程，依据滤波增益矩阵的变化，从监测数据中定量提取有效信息，修正状态参量，从而补偿噪声对数据的影响，有效提高数据处理精度。以滤波值为基础，建立新陈代谢GM(1，1)模型，并预测后4期数据，并分别对于传统GM(1，1)模型、ARMA模型进行对比，结果如表3所示。

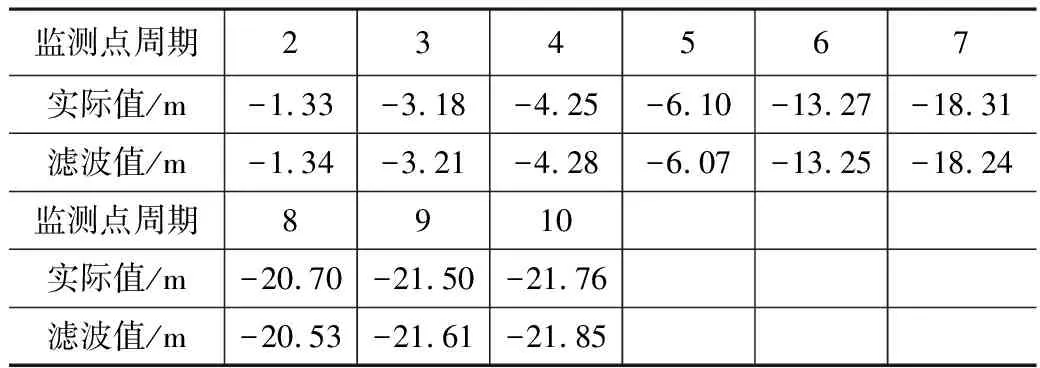
表2 Kalman滤波值与预测值

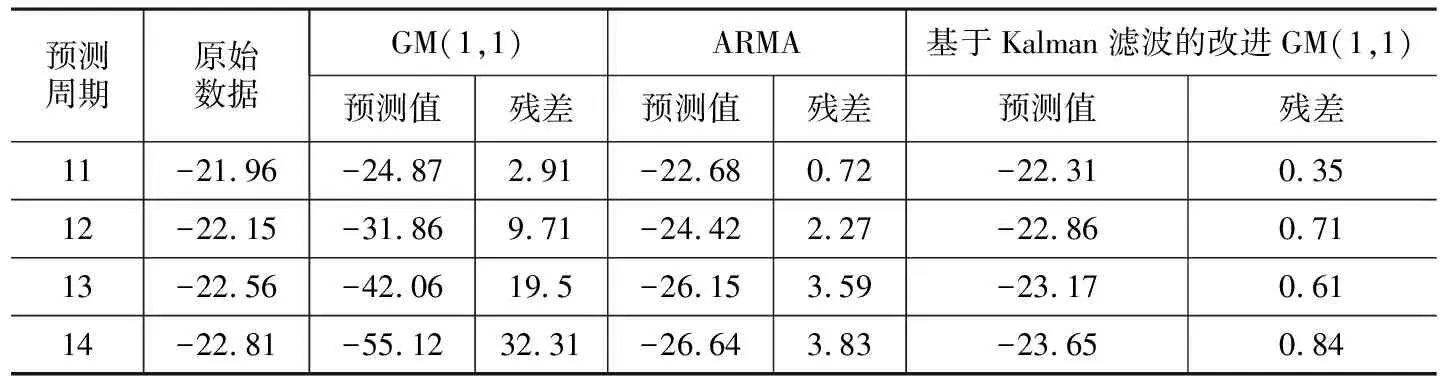
表3 基于Kalman滤波的改进GM(1，1)与传统GM(1，1)、ARMA预测值比较

由表3，图2可知，经卡尔曼滤波处理后的改进GM(1，1)模型具有更高的预测精度，能更好地反映变形趋势，相比于单纯GM(1，1)模型和ARMA模型精度更高。

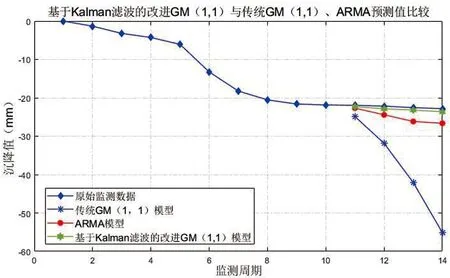
图2 基于Kalman滤波的改进GM(1，1)与传统GM(1，1)、ARMA预测值比较

由表4可知，对比三种模型的预测值、残差值的均方差及中误差，基于Kalman滤波的新陈代谢GM(1，1)相比于传统的单一GM(1，1)、ARMA模型，有效降低了观测噪声影响，并具有更高的预测精度。

表4 三种模型预测精度对比

4 结 论

卡尔曼滤波通过建立状态方程和观测方程来描述系统的动态过程，依据滤波增益矩阵的变化，从监测数据中定量提取有效信息，修正状态参量，从而补偿噪声对数据的影响，有效地提高数据处理精度，结合新陈代谢GM(1，1)模型对变形趋势项进行建模分析，来预测变形趋势。相比于传统的单一GM(1，1)、ARMA模型，有效降低了观测噪声影响，并具有更高的预测精度。但是在使用上述模型时，也要注意以下几点：

(1)Kalman滤波初始值的选取很关键，错误的初始值不能很好反映数据变化趋势；

(2)Kalman滤波的优势在于能实时反映数据变化状态，并通过新数据来更新状态方程，通过增益矩阵来控制观察数据噪声的影响，对提高数据预测精度有很好的效果；

(3)新陈代谢的GM(1，1)模型通过加入新的已知信息，剔除旧的无效信息，来提高预测精度，但也易受到突变信息、粗差信息干扰，导致预测不准。使用模型时，需对新加入的数据做一定的判别和分析。