竖向激励荷载下桩-承台共同作用动力特性试验分析

凡红, 陈合德, 龚维明, 戴国亮, 曹小林

(1.中广核工程有限公司核电安全监控技术与装备国家重点实验室， 广东 深圳 518000； 2.浙江交科工程检测有限公司， 浙江 杭州 311200; 3.东南大学 土木工程学院， 江苏 南京 211189)

近几年，随着中国基础设施建设的快速发展，在桩基础的建设方面也得到快速的发展。由于桩基础的承载力高、沉降量小、能适应各种地质条件和荷载情况的特点而被广泛应用于民用建筑、铁路客运专线、跨海大桥、核电站、海洋石油开采平台以及大型动力机器基础等各种基础工程中。

在实际工程中，桩基础常受到动荷载(如动力检测荷载、交通荷载、地震荷载、波浪荷载和风荷载)的作用，因此其动力特性已得到广泛关注。在分析桩基础的动力响应时，得到桩的位移和刚度至关重要，通过分析桩的位移和刚度随频率的变化规律，研究桩基的动力特性。最早分析桩基动力的方法为Winkler弹性地基梁模型，Winkler弹性地基梁模型是将土体对桩的作用简化为一并联的弹簧和黏壶，建立桩在弹簧和黏壶作用下的动力响应[1-2]。胡昌斌等[3]基于Winkler弹性地基梁模型，研究了桩在纵向振动荷载作用下的振动特性；孔德森[4]对弹性地基梁模型进行了改进，将桩侧土对桩身的作用力用由弹簧、黏壶和滑动元件组成的模型代替，该模型可以模拟桩周弱化土体变形的非线性和桩土界面相对滑移、相对分离等非连续变形。此外，众多学者基于Winkler弹性地基梁模型研究取得了丰硕的成果，这些成果不断地完善了Winkler模型理论[5-8]。基于Winkler模型，Novak[2]提出平面应变模型，该模型假定土体由一系列无穷薄的水平薄层组成，各薄层之间相互独立，土体中位移、应力沿纵向深度无变化，桩土之间完全接触；Yang[9]分析了桩周土径向不均匀性对竖向振动响应的影响；吴文兵等[11]采用平面应变模型并考虑桩的横向惯性效应研究了楔形桩的纵向振动响应。连续介质模型是将桩周土视为三维连续介质，考虑了竖向应力和位移对水平和环向应力与位移的影响，考虑了几何阻尼及材料阻尼对弹性波向外辐射产生的影响[11-12]。基于连续介质模型，Zheng等[13-14]通过直接对土体运动方程进行微分变换，给出了纵向及水平动荷载作用下的振动响应解。饱和土体理论是基于Biot理论，分析考虑饱和土性参数对桩刚度的影响。Zheng等[15]和余俊[16]基于Biot理论，分别分析了管桩饱和土体中管桩的水平振动和端承桩在饱和土中的动力响应。

上述研究成果均为考虑承台的存在产生的作用对桩基承载能力的影响，而在实际工程中桩基包括桩和承台共同承受荷载。该文将基于现场试验进行自由场、单桩和两桩承台的竖向振动，分析桩的存在对桩基竖向加速度、位移幅值和竖向刚度的影响。

1 现场动力试验

1.1 试验介绍

桩基动力试验在南京浦口某工程的场地上进行，试验分为3组，分别为自由场、单桩和两桩承台的激振，承台的详细尺寸见图1。桩身为PHC管桩，内外径分别为150、500 mm，壁厚175 mm。桩身入土深度12 m，自由长度0.2 m，浇筑承台过程中，自由段长度0.2 m嵌入承台中。PHC管桩的预应力钢筋为11φ10.7、有效预应力为6 MPa，开裂弯矩125 kN·m，极限弯矩210 kN·m。承台采用φ12@150双网双向配筋，混凝土为C30。试验之前，浇筑厚度为0.4 m的钢筋混凝土承台，在承台中预埋螺栓，在进行试验前把激振设备固定在承台上。

在竖向强迫激振之前，沿竖向对称布置两个拾振器，用于采集竖向振动产生的加速度；沿竖向对称布置两个位移计，用于采集竖向振动产生的位移。通过动态采集仪收集数据，获得加速度和位移，并通过计算获得桩头刚度。通过旋转质量式激振器进行加载，质量块的总质量为me，偏心距为e，通过偏心质量块提供激振力。设备布置情况见图2。

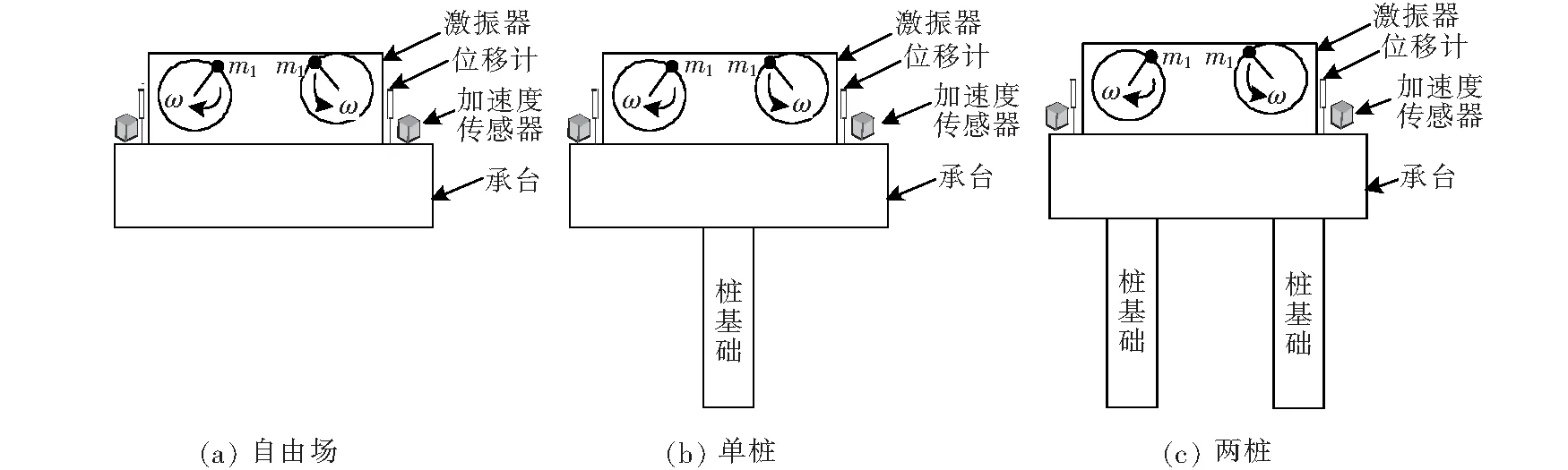
图2 现场激振示意图

1.2 场地地质条件

在南京浦口进行激振荷载下的自由场、单桩和两桩的现场试验。桩周土从上到下为：杂填土、淤泥质粉土、粉砂夹粉土、粉细砂；土层的详细参数见表1，杂填土土性差异较大，表1只给出了杂填土厚度。

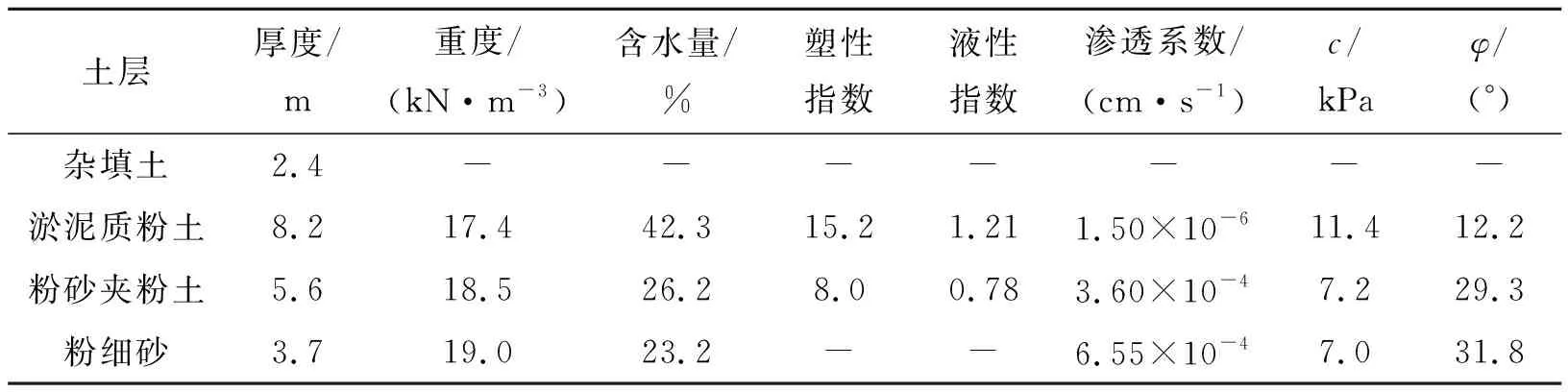
表1 土层参数

1.3 激振荷载

加载设备采用JZQN-30/50动刚度变频多功能激振器，采用配有可控调速器的偏心块机械式激振器，通过改变激振器速度调整激振频率进行竖直激振，设备振动频率为1～50 Hz，竖向激振力为0.09～35.17 kN。桩的激振荷载是由安装在桩承台顶面上的激振器施加，该荷载是由激振器的偏心质量块绕轴旋转而产生，该激振力与转动频率的平方成正比。图3为加载与控制系统图，先通过频率控制器输入频率，激振器接收到信号后，产生幅值为Q0=meeω2的振动荷载，使桩基和承台产生振动，通过加速度传感器和位移传感器将信号传输到电脑。

图3 加载与采集系统

对于旋转质量式激振器，它的总质量m作用在偏心距e处，则产生的激振力为Q(t)=Q0cos(ωt)，其中Q0=meeω2，ω为频率。激振器的频率范围为1～50 Hz。其具体数据见表2。

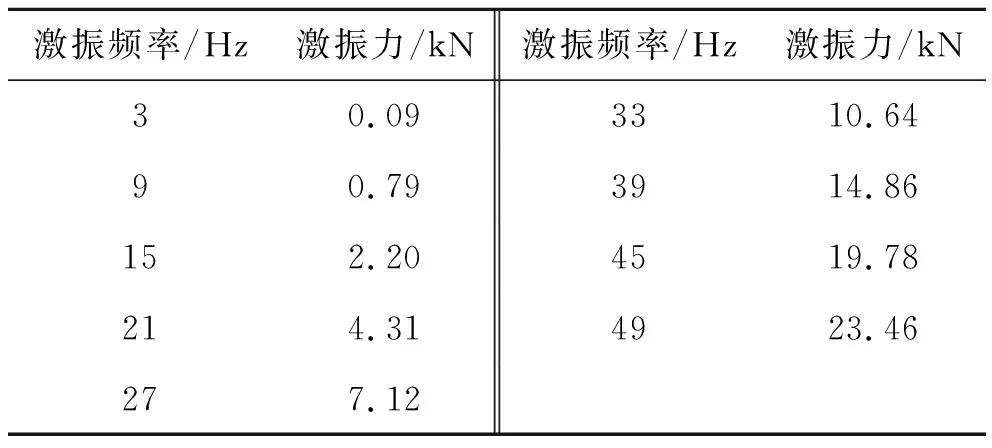
表2 激振频率对应的荷载

2 结果分析

2.1 桩头位移分析

图4为激振荷载作用下自由场、单桩、两桩承台的加速度随着频率的变化曲线。

从图4可得：自由场、单桩和两桩的加速度幅值随着频率的增大而持续增大，这是由于激振力幅值Q0=meeω2是频率的二次方，激振力随着频率的增大持续增大。此外，对比自由场、单桩和两桩的加速度-频率曲线发现，自由场的加速度远远大于单桩和两桩的加速度幅值，单桩桩头加速度幅值约为两桩的2倍。此外，由于两桩在振动过程中，当激振频率达到48 Hz时，个别预埋件的螺丝断丝，无法增大频率继续加载。

图4 加速度-频率曲线

2.2 桩头位移分析

图5为激振荷载作用下自由场、单桩、两桩承台的位移幅值随着频率的变化曲线。从图5可得：自由场和单桩的位移幅值随着频率的增加，呈现先增大后减小的趋势，并出现共振区域，且单桩的共振频率大于自由场的振动频率； 两桩的位移幅值随着频率的增加，呈现先增大后稳定的趋势，并未出现共振区域。另外，对比自由场、单桩和两桩的位移幅值随频率变化曲线发现，自由场的位移幅值远大于单桩和两桩的位移幅值，两桩承台桩基础的位移幅值最小。这是由于桩的存在提高了基础的刚度，使基础的位移降低了很多，改善了基础的承载性能。

图5 激振荷载作用下位移幅值随着频率变化曲线

2.3 刚度分析

2.3.1 计算公式

依据GB/T 50269—2015《地基动力特性测试规范》，竖向阻尼比可以通过式(1)～(4)计算得到:

(1)

(2)

(3)

(4)

式中：ζz为地基竖向阻尼比;ζzi为由第i点计算的地基竖向阻尼比；fm为基础竖向振动的共振频率；βi为位移幅值曲线上选取的第i点振动线位移的比值；fi为幅频响应曲线上选取的第i点的频率(<0.85fm)(Hz)；Ai为幅频响应曲线上选取的第i点的频率所对应的振幅(m)；n为频幅响应曲线上选取计算点的数量。

桩基竖向振动的参振总质量按式(5)、(6)计算:

(5)

(6)

式中：mz为基础竖向振动的参振总质量；fnz为基础竖向无阻尼固有频率(Hz)。

桩基(或地基)抗压刚度和抗压刚度系数、单桩抗压刚度按式(7)～(9)计算:

Kz=mz(2πfnz)2

(7)

(8)

(9)

式中：Kz为桩基(或地基)抗压刚度(kN/m)；Cz为桩基(或地基)抗压刚度系数(kN/m3)；Kpz为单桩抗压刚度(kN/m)；np为桩数。

当固有频率较高不能测出共振峰值时，宜采用低频区段求刚度的方法，其参振质量和单桩抗压刚度按式(10)、(11)计算：

(10)

(11)

式中：P1和P2为幅频响应曲线上选取的第一个点和第二个点对应的激振力；d1和d2为幅频响应曲线上选取的第一个点和第二个点对应的线位移；φ1和φ2为幅频响应曲线上选取的第一个点和第二个点对应的扰力与振动线位移之间的相位角，由测试确定；ω1和ω2为幅频响应曲线上选取的第一个点和第二个点对应的振动圆频率。

2.3.2 结果分析

通过式(2)可得第i点计算的地基竖向阻尼比，把式(2)所得的结果代入式(1)得到自由场和单桩的竖向阻尼比；然后通过式(7)、(8)得到竖向刚度和竖向无阻尼固有频率；由于两桩承台的固有频率较大，未达到共振频率，采用式(9)、(10)计算参振质量和竖向刚度，计算结果见表3。

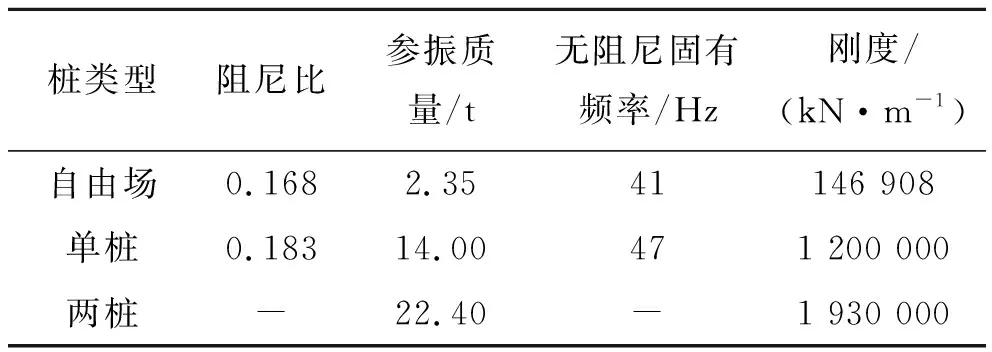
表3 自由场、单桩、两桩承台激振计算结果

由表3可得：自由场的刚度为146 908 kN/m，远小于单桩承台的刚度1 200 000 kN/m，单桩的刚度约为自由场刚度的8倍。说明桩的存在极大地提高了基础的刚度，改善了基础的承载性能；对比单桩和两桩的刚度发现，两桩承台的刚度与单桩承台刚度不存在2倍关系，这是由于两桩作为群桩基础，桩与桩之间存在相互作用影响系数。

3 结论

通过自由场、单桩和两桩承台的现场竖向激振试验，分析桩头加速度、位移幅值和竖向刚度随着频率的变化规律，研究桩与承台共同的承载性能。得出以下结论：

(1) 自由场和单桩的位移幅值随着频率的增加，呈现先增加后减小的趋势，并出现了共振区域，且单桩的共振频率大于自由场的振动频率；两桩的位移幅值随着频率的增加，呈现先增加后稳定的趋势，并未出现共振区域。

(2) 对比自由场、单桩和两桩的位移幅值随频率变化曲线发现，自由场的位移幅值远大于单桩和两桩的位移幅值，两桩承台桩基础的位移幅值最小。这是由于桩的存在改善了基础的承载能力，提高了基础的强度，有效地控制了基础的变形。

(3) 基于规范给出了桩基的刚度计算公式，通过计算发现，自由场的刚度为146 908 kN/m，远小于单桩承台的刚度1 200 000 kN/m，单桩的刚度约为自由场刚度的8倍。

(4) 通过分析自由场、单桩和两桩承台竖向位移幅值曲线和桩基竖向刚度发现，两桩承台的刚度与单桩承台刚度不存在2倍关系。