基于信息量-随机森林耦合模型的山地丘陵县滑坡灾害易发性空间预测

陈 博，王 洋，黄 信，黄精涛

(东华理工大学水资源与环境工程学院，330013，南昌)

0 引言

全国每年平均地质灾害多达1.4万起，其中滑坡灾害约占灾害总数的70%(国土资源部，2010—2016)，造成了巨大的人命财产和经济损失，滑坡已成为中国主要的地质灾害类型之一。科学有效地评价预测滑坡的易发性，可在一定程度上降低灾害带来的损失。目前，常用的滑坡易发性评价模型包括：信息量模型、证据权模型(WEM)、层次分析法(AHP)、逻辑回归模型(LRM)、随机森林模型等[1-4]，国外学者Wei等[5]通过LR模型和 RF 模型对比研究的方法开展滑坡危险性评价，验证结果显示RF模型适用度高于LR模型；Zhao等[6]运用旋转森林(ROF)和RF模型对比开展巴东地区滑坡易发性研究，结果显示 RF 模型精度更高；He等[7]选用RF算法对全球地震诱发的滑坡开展易发性研究，结果表明该模型适用性较好，有助于该类滑坡应急响应的研究。在国内，吴润泽等[8]运用RF模型选取三峡库区湖北段为研究区进行易发性研究，结果显示研究区 3/4左右区域位于较高和高易发区；杨硕等[9]选取乌江地区滑坡为研究对象，运用RF模型对其进行易发性研究，并对评价结果开展了精度验证；管家琳等[10]运用信息量模型与RF模型对比研究龙门镇北部小流域的崩岗风险，结果显示RF模型具有较高的评估精度。一系列国内外研究表明，随机森林模型具有很强的非线性处理能力，且在处理大数据量、高维度数据方面具有很好的泛化能力，预测精度高，适合用于地质灾害易发性评价中[11]，但随机森林模型存在分类精度受不平衡数据影响和投票平局造成算法停滞的问题[12]，而信息量模型可以处理数据分布不平衡的问题。

因此，本文以江西省吉安市新干县为例，建立基于信息量-随机森林耦合模型进行滑坡灾害易发性分区评价，并通过信息量模型进行对比分析，对评价结果使用ROC曲线进行检验，其结果可为地方政府防灾减灾以及规划建设提供科学依据。

1 数据获取与评价方法

1.1 数据来源

地质灾害数据来源于新干县1/5万地质灾害详细调查，DEM数据来源于ALOS，分辨率为5 m；高程、坡度、坡向、平面曲率通过ArcGIS表面分析获得；工程地质岩组和道路来源于新干县1/5万地质灾害详细调查中的MapGIS图件。

1.2 指标体系构建

控制滑坡形成的因素很多，包括基础因素和人类工程活动影响的诱发因素，因此滑坡易发性区划是一个复杂的多元系统[13]。本次研究在野外调查成果的基础上，从基础因素和诱发因素两个方面进行滑坡易发性评价。充分考虑新干县自然地理特征、资料的可获得性、研究范围大小及研究精度等要求，在保证评价有效性的前提下，选取高程、坡向、坡度、工程地质岩组、距道路距离、平面曲率6个评价指标，作为滑坡易发性分区评价的评价指标。

1)高程。高程是坡体内应力值大小的重要影响因素，应力会随着坡高的增加而增加，影响着坡体的势能，从而影响坡体的稳定性[14]。自然斜坡高程一般在50～150 m之间易发生滑坡，大于150 m易发生崩塌。

2)坡向。不同坡向与岩层倾向的空间组合关系不同，对斜坡的稳定性有一定影响[15]。

3)坡度。坡度影响岩土体的天然应力状态，导致自然斜坡形成不同的临空面，从而形成的地质灾害也不一样。坡度一般在10°～45°之间易发生滑坡，大于45°易发生崩塌。

4)工程地质岩组。工程地质岩组是形成地质灾害的物质基础，其决定岩土体强度、应力分布、变形破坏等特征等[16]。一般岩性质地坚硬、结构完整的岩组，产生滑坡的可能性小；而质地松散、结构破碎的岩组，产生滑坡的可能性大。

5)距道路距离。修建道路开挖坡脚、破坏坡面植被，改变斜坡应力分布容易引发崩塌和滑坡地质灾害[17]。

6)平面曲率。平面曲率是等高线弯曲程度的具体量化，其反映的是斜坡在水平方向上的地形变化率，对滑坡发育具有非常重要的影响。平面曲率影响滑坡的表面形态特征，进而影响边坡土地利用类型以及坡体结构特征。

1.3 评价模型的建立

1.3.1 信息量模型 信息量模型(IVM)是把一定地质环境下已经发生变形破坏或可能存在变形破坏的的信息，通过统计分析的方法，计算各影响因素对研究对象所提供信息量大小的统计模型。信息量值越小，说明地质灾害发生的可能性越小；反之信息量值越大，地质灾害越可能发生[18]。对应某种因素特定状态下的地质灾害信息量公式可表示为：

(1)

式中：IAj→B为对应因素A在j状态(或区间)下地质灾害B发生的信息量；Nj为对应因素A在j状态(或区间)下地质灾害分布的单元数；N为调查区已知有地质灾害分布的单元总数；Sj为因素A在j状态(或区间)分布的单元数；S为为调查区单元总数。

由于每个评价单元受众多因素的综合影响，各因素又存在若干状态，各状态因素组合条件下地质灾害发生的总信息量可用公式(2)确定：

(2)

式中：I为对应特定单元地质灾害发生的总信息量；Ni为对应特定因素在第i状态(或区间)条件下的地质灾害面积或地质灾害点数；N为调查区地质灾害总面积或总地质灾害点数；Si为对应特定因素在第i状态(或区间)的分布面积；S为调查区总面积。

1.3.2 信息量-随机森林耦合模型 随机森林( RF )是由Breiman[19]首次提出机器学习中基于多个决策树的分类智能算法。信息量-随机森林耦合模型的总样本由灾点与非灾点1:1构成，其中总样本信息为各评价指标的信息量值，将总样本再分为训练集与测试集，利用训练集生成决策树模型，再将测试集代入决策树模型中，得到分类结果，最后通过投票进行预测分类。由于每颗决策树的训练样本及节点分裂属性均为随机选取，在一定程度上避免了模型的过拟合现象[20]。采用RF模型进行分类预测的流程见图1。

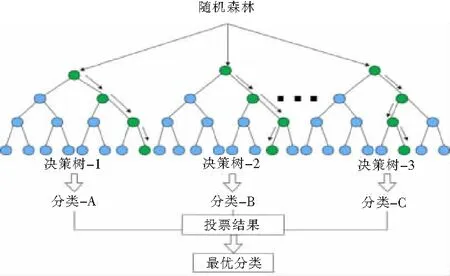
图1 随机森林(RF)模型分类预测流程图

1.4 评价结果与对比验证

基于信息量-随机森林耦合模型的评价模型先计算出每个样本的信息量值，再利用 MATLAB软件编好的RF代码进行训练，得到各指标的客观权重，再将各评价指标专题图和MATLAB软件得到的权重值在 ArcGIS 10.5软件经加权总和工具进行叠加，而信息量模型直接将各评价指标专题图的信息量叠加，得到2个模型全区的滑坡易发性图。采用自然间断点法将易发性区域划分为5个等级，分别为低易发区、较低易发区、中易发区、较高易发区、高易发区。最后采用ROC曲线进行验证，AUC值高的模型，其预测精度更高，更适合此研究区的滑坡易发性评价。

2 实例分析

2.1 研究区概况

研究区位于江西省新干县，总面积1 245.38 km2(115°14′48″～115°43′54″E，27°30′09″～27°57′50″N)，属亚热带季风气候，年平均气温为17.6 ℃，年平均降雨量为1 579.2 mm，最大年降雨量2 295.9 mm(2012年)，属赣江流域。研究区地形以中低山-丘陵为主，地层发育较齐全，分别为第四系松散岩组、红色碎屑岩组、一般碎屑岩组、碳酸盐岩组、变质岩组、岩浆岩组。研究区构造复杂。

2.2 评价指标选取与指标体系建立

本文通过收集影响滑坡发生的相关基础数据，最初选取高程、坡度、坡向、工程地质岩组、平面曲率、距道路距离、距断层距离、距水系距离8个评价指标，但由于距断层和水系近的地方滑坡不发育，而距离远的地方滑坡反而发育。最终选取高程、坡度、坡向、工程地质岩组、平面曲率、距道路距离6个评价指标进行滑坡易发性评价。各评价指标分级图如图2。

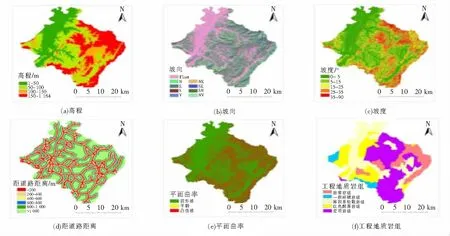
图2 各评价指标分级图

2.3 基于信息量-随机森林模型的滑坡灾害易发性评价

利用 ArcGIS 10.5软件值提取至点工具提取研究区 291个滑坡点各评价指标的属性数据，标记为“1”，接着选取与滑坡点数量相同的非滑坡点，提取291个非滑坡点各评价指标的属性数据，标记为“0”。用高程、坡度、坡向、工程地质岩组、平面曲率、距道路距离的信息量值与是否为灾点(1为灾点，0为非灾点)构成模型的总样本。随机选取滑坡点及非滑坡点样本中的70%(407个)作为训练样本，剩下的30%(175个)作为测试样本。利用MATLAB软件，将训练样本代入编好的代码进行训练，训练之后的模型用于测试样本，随后调用重要性函数得到各评价指标的权重如图3所示。

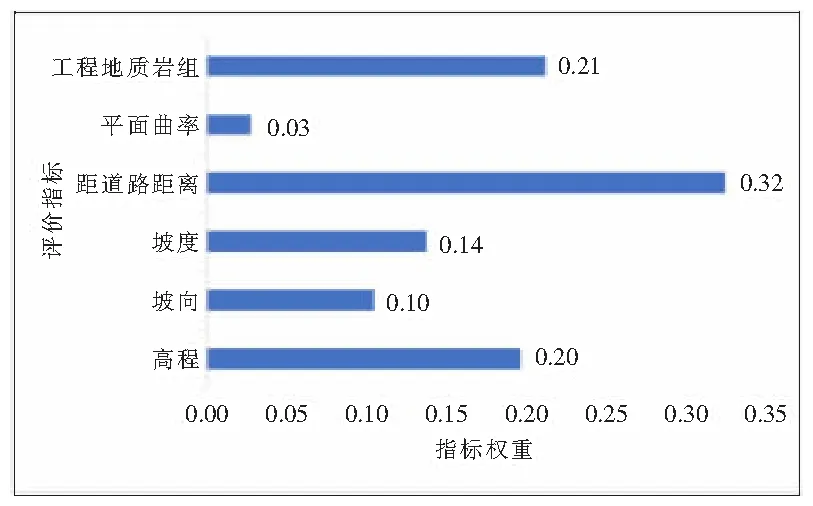
图3 评价指标权重图

2.4 基于信息量模型的滑坡灾害易发性评价

使用 ArcGIS 10.5软件分别将6个评价指标与滑坡点位分布图叠加，计算各个指标类对应的滑坡数量，由公式(1)得出评价指标对应的信息量值(表1)。

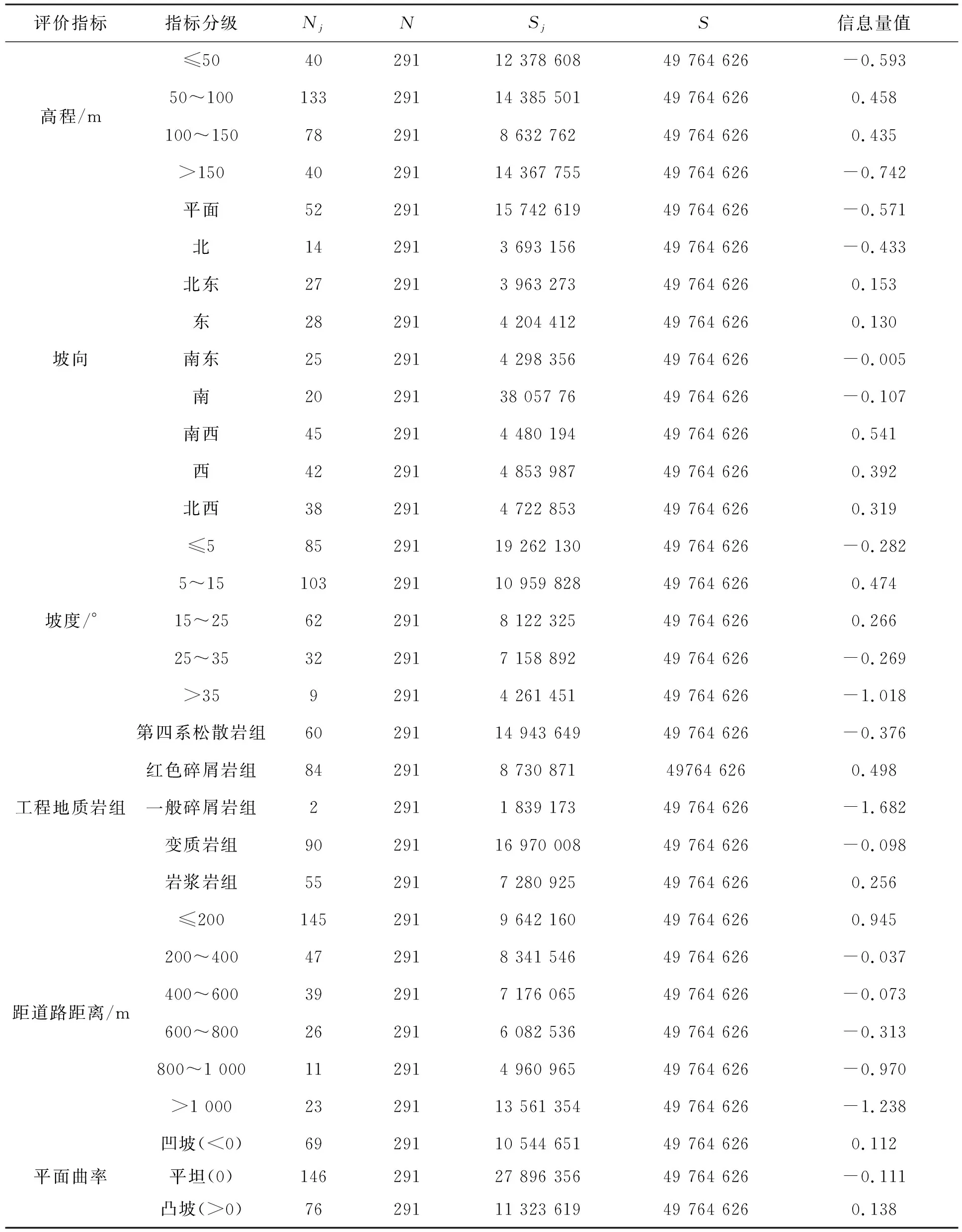
表1 评价指标信息量表

在信息量模型中，信息量值反映了评价指标对滑坡发生的可能性大小，值越大则表示对滑坡发生的可能性越大，负值则表示不利于滑坡的形成[21]。由表 1可知，信息量值较大的评价指标类分别是：高程为50～150 m；坡向为南西、西和北西方向；坡度为5°～25°；工程地质岩组为红色碎屑岩组；距道路距离为200 m以内；平面曲率为凸坡。总体来看，距道路距离对滑坡的影响最大，其次为工程地质岩组、高程、坡向、坡度，而平面曲率则是对滑坡发生影响最小的评价指标。

2.5 滑坡易发性评价结果与ROC对比验证

2.5.1 滑坡易发性评价结果 将各评价指标专题图和MATLAB 软件得到的权重值在 ArcGIS 10.5软件经栅格计算器工具进行叠加，得到全区的滑坡易发性图。采用自然间断点法将易发性区域划分为5个等级，分别为低易发区、较低易发区、中易发区、较高易发区、高易发区。生成的滑坡易发性分区图如图4所示。

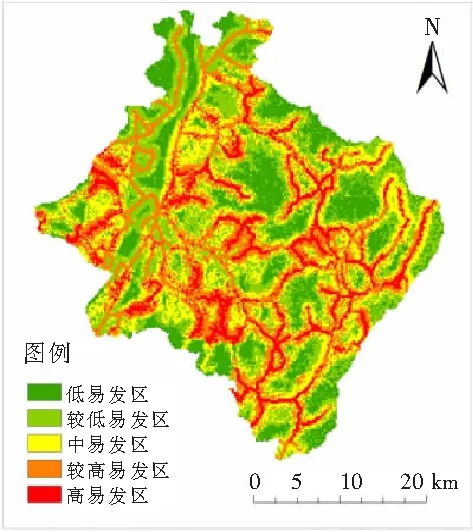
图4 基于信息量-随机森林模型的滑坡易发性分区图

将表1中各评价指标分级的信息量值代入公式(2)得到各评价指标的总信息量I，借助 ArcGIS 10.5软件计算得到该模型下的研究区滑坡的易发性图，采用自然间断点法将易发性区域划分为5个等级，分别为低易发区、较低易发区、中易发区、较高易发区、高易发区，等级划分后生成滑坡易发性分区图如图5所示。

图5 基于信息量模型的滑坡易发性分区图

结合图4和图5可知，信息量模型得出的滑坡易发性分布趋势与信息量-随机森林模型预测结果大致相同，较高易发区和高易发区均呈线性分布在道路附近，影响滑坡的主控因素均为距道路距离。

2.5.2 ROC对比验证 为对比评价信息量-随机森林模型和信息量模型的预测精度，采用受试者特征曲线(ROC)对两种模型的空间预测性能进行检验。通常用曲线与X坐标轴围成的面积(AUC)来评价模型的预测性能，AUC值越大，其预测效果越好[22]。利用SPSS软件绘制出两种模型的ROC曲线图如图6所示。

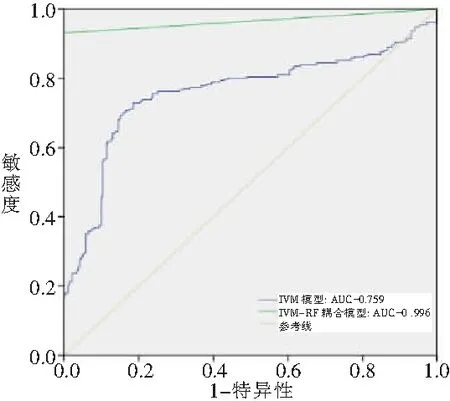
图6 ROC曲线

由图6可知，信息量-随机森林模型及信息量模型的AUC值分别为0.966和0.759，其中信息量-随机森林模型较信息量模型的预测精度高了20.7%。

3 结论

1)对评价指标分析可以得出，在信息量-随机森林模型和信息量模型中最为显著的评价指标都是距道路距离，其中信息量-随机森林模型中次重要的评价指标依次为工程地质岩组和高程，而信息量模型次重要的评价指标依次为坡向、工程地质岩组和坡度。

2)信息量-随机森林模型得出的滑坡易发性分布趋势与信息量模型预测结果大致相同，滑坡高易发区和较高易发区呈线性分布在道路附近，影响滑坡的主控因素为距道路距离。

3)由ROC曲线可知，信息量-随机森林模型及信息量模型的AUC值分别为0.996和0.759，其中信息量-随机森林模型较信息量模型的预测精度高了20.7%，说明信息量-随机森林模型更适合此研究区的滑坡易发性评价。