基于能量法的刚构桥合龙顶推位移计算方法

王 磊, 杨国俊, 刘晓健, 刘志华

(1.中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065; 2.山西省交通科技研发有限公司 桥梁工程防灾减灾山西省重点实验室,山西 太原 030032; 3.兰州理工大学 防震减灾研究所,甘肃 兰州 730050; 4.陕西省高速公路建设集团公司,陕西 西安 710075)

穿越黄土山区沟壑地形的高墩大跨连续刚构桥,“T”构合龙温度与设计合龙温度偏差及成桥后期混凝土收缩徐变使桥墩发生纵向位移,导致高桥墩处于压弯复合受力状态。为减小合龙温差及材料时间效应对结构的不利影响,工程上普遍的做法是在刚构桥合龙时,在“T”构悬臂端进行顶推施工,同时控制顶推位移和顶推力[1]。顶推过程相当于人为迫使桥墩发生反向位移,恰好能够抵消合龙温差及材料时间效应的结构变形,而顶推位移的确定成为刚构桥合龙施工的关键。

目前,多跨刚构桥合龙顶推的相关研究成果较丰富。文献[2]推导了三跨混合梁刚构桥在施工和成桥阶段的简化力学模型,并通过实桥工程实践验证其正确性;文献[3]通过分析2座连续刚构桥墩身变位与顶推力之间相互关系,从设计角度提出大跨高墩连续刚构桥顶推力控制基本原则;文献[4-10]采取多点连续顶推措施,对连续刚构桥多个合龙口进行一次合龙,并对箱梁局部受力进行分析;文献[11-12]分别分析非常规合龙顺序对多跨连续刚构桥成桥状态的影响,并对多跨刚构桥合龙顺序提出相关建议;文献[13]基于力法原理，提出一种适用于单柱式墩连续刚构桥顶推力的计算方法,并以某刚构桥顶推施工为例进行验证;文献[14]用力法方程推导薄壁墩刚构桥合龙顶推力的解析法计算公式,并与有限元计算结果及实际顶推结果进行对比;文献[15]实测某矮墩连续刚构桥合龙过程中的顶推力及顶推位移,并与理论值进行对比分析。

已有相关理论基本能够满足实际工程需求,为刚构桥合龙顶推控制问题提供较全面的技术参考及依据,但对于刚构桥合龙顶推过程的力学特征,尤其是高桥墩的非线性效应对结构的影响,缺乏深入分析。

本文根据最小势能原理,采用Rayleigh-Ritz法，全面考虑连续刚构桥高桥墩在顶推过程中可能位移状态下的应变能与荷载势能,提出刚构桥合龙顶推位移计算公式,并以某大桥合龙顶推控制过程为例,对提出的刚构桥合龙顶推位移计算方法进行验证。

1 采用Rayleigh-Ritz法的能量方程

以典型三跨连续刚构桥为例,刚构桥合龙顶推施工如图1所示。图1中:P为悬臂端合龙口顶推力;e为顶推力合力水平作用线与桥墩顶处的竖向距离;E为桥墩弹性模量;I为桥墩截面惯性矩;l为桥墩高。在顶推力P作用下,高桥墩受力模型如图2所示,桥墩承受水平推力P、上部所有悬臂节段自重N、墩身每延米自重q及墩顶偏心力矩M0。

根据位移边界条件,高桥墩变形曲线可表示为:

(1)

其中:a为顶推力作用下的墩顶侧向位移,即顶推位移。

桥墩在可能位移状态下的势能Π为:

Π=U+UP

(2)

其中:U为桥墩应变能;UP为桥墩的荷载势能。

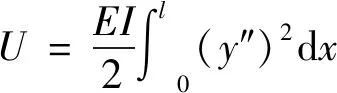
(3)

UP=-Nλ-Pa-

(4)

其中:λ为顶推力作用下桥墩顶的竖向位移;θ为桥墩顶转角变形。则有：

(5)

(6)

M0=Pe

(7)

将(1)式、(6)式、(7)式代入(5)式,则有:

(8)

由(1)式可得:

(9)

将(9)式代入(8)式,计算可得:

(10)

势能驻值条件为:

(11)

则顶推位移计算公式为:

(12)

对(12)式进一步化简可得:

(13)

(14)

(14)式与文献[16]结果一致,由(14)式可以看出,分母实质上是计入垂直力效应的高桥墩抗推刚度,用k墩表示。令N、q取值均为0,可得到不计重力二阶效应的高桥墩横向抗推刚度,即

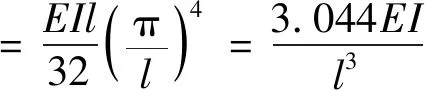
(15)

(15)式与裸墩的横向抗推刚度静定解[17]已相当接近,该静定解为:

k墩=3EI/l3

(16)

(12)式为连续刚构桥合龙顶推位移的Rayleigh-Ritz解析解。由(12)式可知:a受P、N、q和M0影响;对于顶推施工阶段的刚构桥“T”构,P、N、q及e为定值,a与P呈线性变化关系，P越大,a越大。

2 实例分析

2.1 工程概况

常家河特大桥位于包头—茂名高速陕西省境内的铜川至黄陵公路铜川新区至何家坊段。主桥结构为(75+2×140+75) m预应力混凝土连续刚构,5#、6#、7#主桥墩均为单薄壁空心墩,最大墩高85.8 m(6#墩)。主桥设计合龙温度为12°,按照实际施工进度,合龙时间在7月初,合龙期间实测气温远高于设计温度,必须考虑合龙温差的影响。合龙温度24 h监测结果如图3所示。

为确定不同温度下的顶推力施加值,通过有限元法模拟施工阶段,考虑5 a收缩徐变及降温温差效应,分别计算降温4、8、12 ℃(对应合龙温度16、20、24 ℃)及收缩徐变产生的墩顶偏位值,并计算单位顶推力产生的顶推位移，由此得到降温温差与顶推力之间的线性回归关系[4]为:

P1=32.1ΔT+872

(17)

P2=27.0ΔT+741

(18)

其中:P1、P2分别为5#～6#、6#～7#桥墩之间合龙口处施加的顶推力;ΔT为监测温度与设计合龙温度温差。

2.2 计算对比

桥墩采用C40混凝土,弹性模量考虑钢筋影响,取值为39.5 GPa;由于单薄壁空心墩实心部分惯性矩远大于空心段,各桥墩截面惯性矩取平均值,并调整各桥墩计算高度。主桥采用一次合龙方案,监测合龙温度为24 ℃,确定合龙顶推力P1=1 257 kN,P2=1 065 kN。主桥计算参数取值见表1所列。顶推位移计算结果见表2所列。

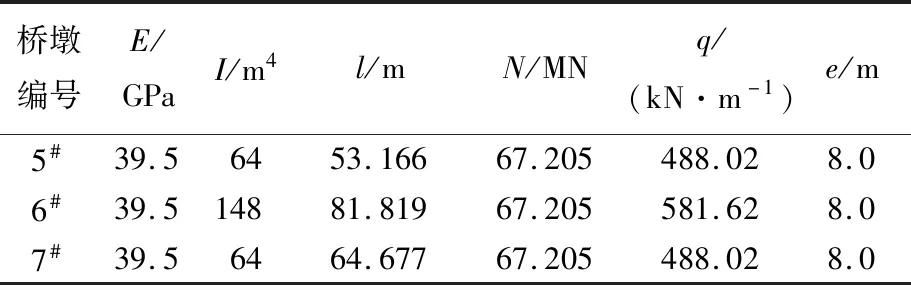
表1 主桥计算参数取值

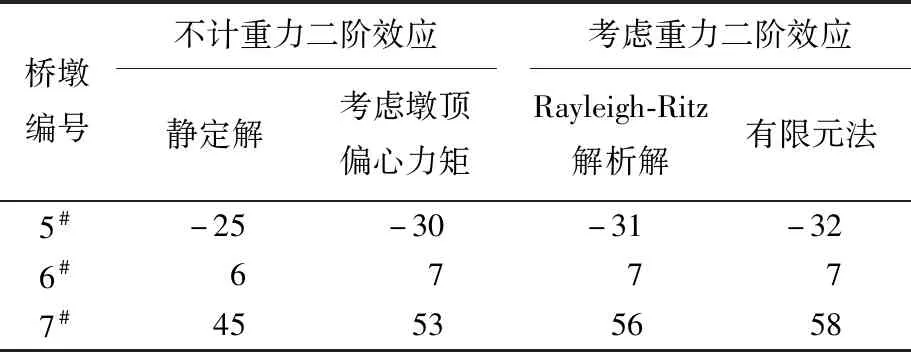
表2 顶推位移计算结果对比 单位:mm

由表2可知:由Rayleigh-Ritz解析解得到的刚构桥合龙顶推位移与有限元法结果最大偏差为3.6%;Rayleigh-Ritz解析解计算结果与不计重力二阶效应时,考虑墩顶偏心力矩结果较为接近(最大偏差5.4%),与静定解最大偏差为19.6%。由此可见,在进行刚构桥合龙顶推位移计算时,墩顶偏心力矩影响较大,不能忽略;基于Rayleigh-Ritz解析解推导的刚构桥合龙顶推位移计算公式误差很小,能够满足实际工程精度需要。

2.3 顶推方案

主桥4个合龙口采用一次合龙方案,在合龙口A(5#～6#墩之间)、B(6#～7#墩之间)同时布置液压式千斤顶进行合龙顶推施工。在顶推过程中,对顶推力和顶推位移实施双控,根据墩顶实际位移,现场调整顶推力施加大小;顶推力共分9级施加,第9级时,A、B合龙口顶推力均累计至1 400 kN,顶推施工结束,焊接A、B合龙口劲性骨架。主桥合龙过程A、B合龙口处的顶推力见表3所列。

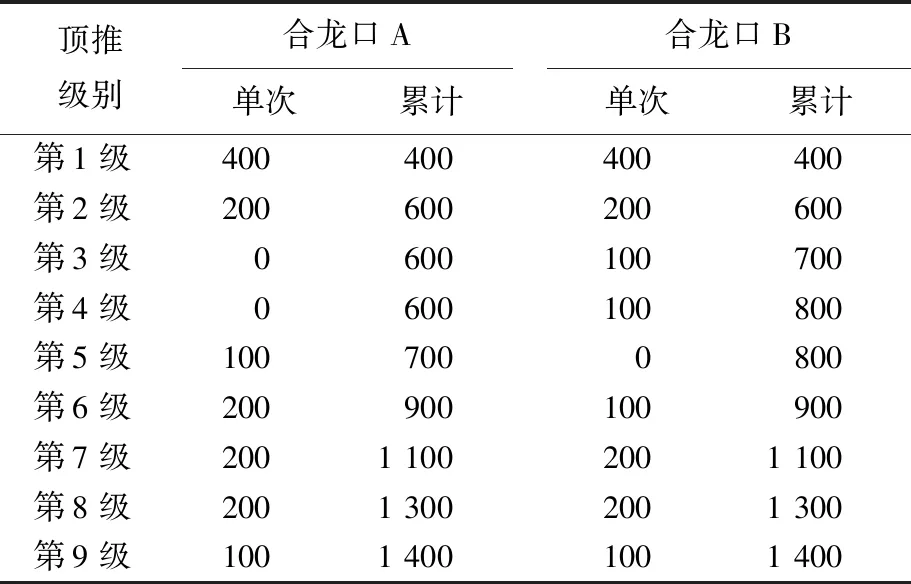
表3 主桥合龙过程A、B合龙口处的顶推力 单位:kN

2.4 顶推结果分析

合龙过程5#～7#墩顶推位移结果如图4～图6所示。从图4、图6可以看出:

(1) Rayleigh-Ritz解析解、不计重力二阶效应及静定解均大于实测值,这是由于力学模型(图2)中未考虑现场施工因素对悬臂端边界约束的影响。

(2) 第9级顶推荷载作用下,Rayleigh-Ritz解析解与设计值(5 a收缩徐变+降温12 ℃)较为接近,5#、7#墩与设计值的误差分别为9.4%、11.0%,说明解析解能够满足设计要求。

(3) 不计重力二阶效应的顶推位移变化与Rayleigh-Ritz解析解极为吻合,说明刚构桥合龙顶推时,重力二阶效应对墩顶位移影响有限。

(4) 相比于不计重力二阶效应的顶推位移,静定解明显较小,且随着顶推力增大,差异明显变大,静定解趋近于实测值,这主要是由于静定解未考虑重力二阶效应及墩顶偏心力矩,而重力二阶效应对顶推位移的影响有限,可判定墩顶偏心力矩对顶推位移的影响不容忽视。

6#墩位于A、B合龙口之间,高度为85.8 m,相对于5#、7#墩,抗推刚度较小。在顶推过程中,其主要作用是平衡A、B合龙口顶推力大小,微调顶推位移。从图5可以看出,A、B合龙口顶推力相等时,6#墩顶理论上保持不动,顶推输出推力不平衡时,墩顶出现较明显的侧向位移;偏心力矩的附加效应也较显著。

3 参数分析

从上述分析可知,重力二阶效应及墩顶偏心力矩对刚构桥顶推位移影响较大。3种计算方法不同墩高下的顶推位移计算结果如图7所示。

由图7可知:墩高增大,顶推位移呈非线性增大变化;桥墩高度较小时,Rayleigh-Ritz解析解与不计重力二阶效应结果差异很小;墩高40～60 m时,偏差仅为2.2%～4.5%,Rayleigh-Ritz解析解与静定解偏差范围在33.3%～26.3%之间;桥墩高度为100 m时,Rayleigh-Ritz解析解与不计重力二阶效应结果偏差为15.1%,与静定解的计算结果偏差达到29.8%。

Rayleigh-Ritz解析解包含了重力二阶效应和墩顶偏心力矩2个因素。相对于静定解,不同因素对顶推位移的影响情况如图8所示。从图8可以看出:随着墩高增大,重力二阶效应对顶推位移的影响程度不断增大,而墩顶偏心力矩影响程度显著降低;墩高超过90 m时,重力二阶效应对顶推位移的影响大于墩顶偏心力矩,其总体表现为桥墩高度超过70 m后,Rayleigh-Ritz解析解与静定解的偏差有所增大。

综上所述,刚构桥顶推位移静定解一般能够满足施工精度要求,其计算结果可作为现场施工顶推位移控制依据;进一步判断参数变化对其影响时,对于一般刚构桥(墩高在50～70 m之间),墩顶偏心力矩影响较大,不能忽视;桥墩高度较高时(墩高在70～90 m之间),重力二阶效应与墩顶偏心力矩应同时计入;超高桥墩(墩高大于90 m)顶推位移计算需重点考虑重力二阶效应的影响。

4 结 论

(1) 基于能量法计算的刚构桥合龙顶推位移计算结果与有限元法分析结果的最大偏差为3.6%,说明推导的计算公式精度较高,能够满足工程计算要求。

(2) 刚构桥实际合龙顶推过程中,Rayleigh-Ritz解析解与不计重力二阶效应结果较为接近,静定解计算结果偏小,这是由于重力二阶效应和墩顶偏心力矩对顶推位移的影响程度不同。

(3) 刚构桥桥墩高度增大,Rayleigh-Ritz解析解与不计重力二阶效应结果、静定解的偏差均变大,最大偏差分别为15.1%、29.8%;重力二阶效应和墩顶偏心力矩对墩高变化敏感性不同,一般刚构桥不能忽视墩顶偏心力矩,超高桥墩顶推位移计算需重点考虑重力二阶效应的影响。