分子信标在一类特殊的整数规划问题中的应用

徐如解, 殷志祥, 唐 震, 杨 静, 崔建中, 王夕远

(1.安徽理工大学 数学与大数据学院,安徽 淮南 232001; 2.上海工程技术大学 数理与统计学院,上海 201620; 3.安徽理工大学 电气与信息工程学院,安徽 淮南 232001; 4.淮南联合大学 计算机系,安徽 淮南 232001)

随着科技的发展,在应对海量的数据信息处理时,传统计算已无法满足要求,人们不得不开始探索新型的计算领域。自文献[1]提出利用DNA计算解决有向Hamilton路径以来,DNA计算受到越来越多研究人员的关注;文献[2-4]介绍了几种不同的DNA计算模型，着重介绍了DNA计算的广泛应用性;文献[5]利用DNA折纸术建立了动态与非门计算模型;文献[6]利用DNA折纸术和杂交链式反应构建了一种新的求解背包问题计算模型。

分子信标是一种荧光标记的寡核苷酸链,通常用作光学探针，具有高灵敏度、易操作以及低检测成本等优点,因此广泛地应用于DNA计算中。文献[7]首次建立分子信标探针,分子信标探针作为一种新型的荧光探针广泛地应用于实时PCR检测[8]、荧光生物传感器[9]及最大匹配问题等[10];文献[11-13]介绍了分子信标在求解0-1整数规划问题、临床检测凝血酶以及生物荧光的IFN-小波冲击检测方法中的应用,并指出利用分子信标模型求解此类问题具有高信息量和易操作化等优点。

整数规划问题是数学规划问题中的一个重要分支,它要求全部或部分决策变量取值为整数，广泛应用于多种问题,如线路设计、背包问题、分派问题等。文献[14-17]介绍了几种求解整数规划问题最优解的计算模型,这些模型的提出进一步说明了DNA计算独特的优势;文献[18]利用DNA折纸术完成了对一类特殊的整数规划问题的求解,该方法具有高度的容错性。

本文设计了一种固定在金(Au)表面上的分子信标模型,用于求解一类特殊的整数规划问题。该模型将变量映射成Au表面上的分子信标,以不同的输入链表示变量不同的取值,并根据荧光信号的颜色和明灭来展示和检测规划问题的结果。

1 分子信标和特殊整数规划问题

1.1 分子信标模型

分子信标是一种荧光标记的寡核苷酸链，一般由环状区、茎干区、荧光基团和淬灭基团3个部分组成。在分子信标的茎环结构中,环一般包含有15～30个脱氧核糖核苷酸,作为识别区与靶分子序列发生碱基互补配对;茎一般包含5～7个脱氧核糖核苷酸,并且相互配对形成茎的结构,同时,在3′端包含一个猝灭基团,在5′端包含一个荧光基团。

具体过程如图1所示。

当维持发夹结构时,猝灭基团-荧光基团靠近会阻断荧光信号的释放;当检测到互补的DNA靶分子时,DNA靶分子与分子信标中的识别区发生碱基互补配对,致使分子信标的发夹结构打开,荧光基团不再受猝灭基团的影响,从而出现荧光信号。

1.2 特殊的整数规划问题

整数规划问题是数学规划的一个重要分支,下面给出整数规划的一般形式。

max(min)u=c1x1+c2x2+…+cnxn;

(1)

其中:max(min)u为整数规划问题的目标函数;大括号中的所有式子是整数规划的约束条件。对于约束条件中的bi,在计算过程中可以看作bi>0。

当bi<0时,不等式两边同时乘以-1,就能够使得bi成为大于0的数。

本文基于分子信标的作用机制,对下述一类特殊的整数规划问题给出了一种新的求解算法。

max(min)u=c1x1+c2x2+…+cnxn;

(2)

下面给出该类特殊整数规划问题的推导过程。(3)式给出整数规划中变量x取值分别为-1、0、1的一般形式:

max(min)u=c1x1+c2x2+…+cnxn；

(3)

对(3)式中的任意一个约束条件,as1x1+as2x2+…+asnxn≤(=,≥)bs,s∈[1,m],如果令xj=xj1,j∈[1,n],那么(3)式中的任意一个约束条件都可以分解为:

max(min)u=c1x1+c2x2+…+cnxn;

(4)

其中：当asj>0时,λasj=1;当asj=0时,λasj=0;当asj<0时,λasj=-1。这个分解形式中,系数|asj|≠0,1变量可以分解成|asj|个相等的变量xs1,xs2,…,xs|asj|。且系数λasj的存在可以保证系数asj在分解前后正负符号不变。由此分解得到一个特殊的整数规划问题。

max(min)u=c1x1+c2x2+…+cnxn;

(5)

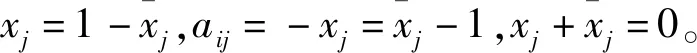
2 分子信标求解特殊整数规划问题

2.1 固定在Au表面上的分子信标模型的构建

根据分子信标的作用原理,本文提出了一种固定在Au表面的分子信标模型。该模型中,Au表面用于固定分子信标链,并且取代了分子信标3′端处的猝灭基团,这是由于Au表面对某些荧光基团具有猝灭能力[19]。3种DNA分子链的设计及其具体的反应原理如图2所示。

从如图2a可以看出,分子信标是一个DNA发夹结构,组成部分为:5′-a-b-a*-3′,其中区域b是分子信标的识别区域,区域a和a*碱基互补配对形成分子信标的茎。在茎的5′端连接有一个二硫化物(S),茎的3′端连接有绿色的荧光素(λem=520 nm)。输入链IA是DNA单链,组成部分为:3′-a*-b*-a*-5′。输入链IB也是DNA单链,组成部分为:3′-a-b*-a-5′。在DNA链的3′端带有一个Cy5(一种红色荧光,λem=694 nm),且输入链IB的5′端携带有分子信标茎3′端绿色荧光素的猝灭基团。同时,a-a*、b-b*遵循沃森克里克碱基互补配对原则,因此输入链IA和IB都可以打开分子信标的发夹结构。

从如图2b可以看出,当没有输入链IA和IB存在时,信标分子3′端存在的绿色荧光基团仍然停留在Au表面附近,此时没有荧光信号产生,代表变量取值为0;当输入链IA存在时,分子信标将会打开发夹结构。此时分子信标3′端的绿色荧光基团远离Au表面,从而释放绿色荧光信号,代表变量取值为1;当输入链IB存在时,分子信标将会打开发夹结构。

输入链IB的5′端的猝灭基团与分子信标3′端的绿色荧光基团结合,绿色荧光猝灭,从而只能观察到来自输入链IB上Cy5的红色荧光信号,代表变量取值为-1。

根据上述固定在Au表面的分子信标模型反应示意图,本文设计了一种固定在Au表面的分子信标模型,用于求解(2)式这一类特殊的整数规划问题。具体思路是:首先将约束条件中的n个变量x1,x2,…,xn设计成n种分子信标固定在Au表面上。其次对于任意一个变量xi(i=1,2,…,n),设计出2种不同的输入链IAi和IBi,通过添加不同的输入链IAi和IBi来表示变量的不同取值。即当xi=0时,不添加输入链IAi和IBi,无荧光信号产生;当xi=1时,向试管中添加输入链IAi,试管中有绿色荧光信号产生;当xi=-1时,向试管中添加输入链IBi,试管中有红色荧光信号产生。最后根据荧光信号的结果来判断解的可行性。以约束条件x1+x2+x3≥2为例,如图3所示。图3中,i=1,2,3。约束条件中有3个变量,因此在Au表面上固定3个分子信标,分别表示变量x1、x2、x3,当变量x1、x2、x3分别取0,1,-1时,向试管中加入输入链IA2和IB3,有一个红色荧光和一个绿色荧光信号产生,即输出结果为0(≤2),因此(0,1,-1)不是约束条件x1+x2+x3≥2的可行解。

综上所述,对于含有n个变量、m个约束方程的整数规划问题,给出(2)式这类整数规划计算模型的具体算法步骤。

(1) 根据问题中n个变量,每个变量取-1、0或1,给出问题的所有可能解(x1,x2,…,xn)的组合,共3n个可能解,取3n个试管。

(2) 根据第1个约束条件中n个变量,首先设计出n种分子信标固定在同一个Au表面上,并置于试管中;然后根据可能解(x1,x2,…,xn)的取值,向试管中加入不同的输入链。具体地,对于任一个变量xi(i=1,2,…,n),通过添加不同的输入链IAi和IBi表示变量的不同取值。即当xi=0时,不添加输入链IAi和IBi;当xi=1时,向试管中添加输入链IAi;当xi=-1时,向试管中添加输入链IBi。

最后根据荧光信号判断出第一个约束条件的可行解。

(3) 重复步骤(2),直到完成规划问题中所有约束条件,最后保留的可行解就是满足所有约束条件的可行解。

(4) 分别计算出各可行解对应的目标函数值并进行比较,最终判断出最优解。

2.2 实例分析

下面以一个包含3个变量、3个子句的整数规划问题来介绍具体的操作过程。

minz=2x1+3x2+2x3;

(6)

(1) 问题中含有3个变量,共有33=27个可能解。分别为:(-1,-1,-1)、(-1,-1,0)、(-1,-1,1)、(-1,0,-1)、(-1,0,0)、(-1,0,1)、(-1,1,-1)、(-1,1,0)、(-1,1,1)、(0,-1,-1)、(0,-1,0)、(0,-1,1)、(0,0,-1)、(0,0,0)、(0,0,1)、(0,1,-1)、(0,1,0)、(0,1,1)、(1,-1,-1)、(1,-1,0)、(1,-1,1)、(1,0,-1)、(1,0,0)、(1,0,1)、(1,1,-1)、(1,1,0)、(1,1,1)。取27个试管进行接下来的生物操作。

(2) 对第1个约束条件x1+x2+x3≥1,设计出3种编码不同的分子信标固定在Au表面,分别表示变量x1、x2、x3。对变量x1设计出2种输入链IA1、IB1,对变量x2设计出2种输入链IA2、IB2,对变量x3设计出2种输入链IA3、IB3。

部分可能解(-1,-1,-1)、(-1,0,1)、(1,1,-1)、(1,1,0)的示意图如图4所示。

对于可能解(-1,-1,-1),向试管中加入输入链IB1、IB2、IB3,试管中出现3个红色荧光信号,表示输出结果为-3,小于1,故(-1,-1,-1)不是第1个约束条件的可行解;对于可能解(-1,0,1),向试管中加入输入链IB1、IA3,试管中出现一个绿色荧光和一个红色荧光信号,表示输出结果为0,小于1,故(-1,0,1)不是第1个约束条件的可行解;对于可能解(1,1,-1),向试管中加入输入链IA1、IA2、IB3,试管中出现2个绿色荧光和1个红色荧光信号,表示输出结果为1,不小于1,故(1,1,-1)是第1个约束条件的可行解;对于可能解(1,1,0),向试管中加入输入链IA1、IA2,试管中出现2个绿色荧光信号,表示输出结果为2,大于1,故(1,1,0)是第1个约束条件的可行解。27个可能解在第1个约束条件下是否是可行解的情况见表1所列。

由表1可知,满足第1个约束条件的可行解有10个,分别记为:1(-1,1,1)、2(0,0,1)、3(0,1,0)、4(0,1,1)、5(1,-1,1)、6(1,0,0)、7(1,0,1)、8(1,1,-1)、9(1,1,0)、10(1,1,1)。

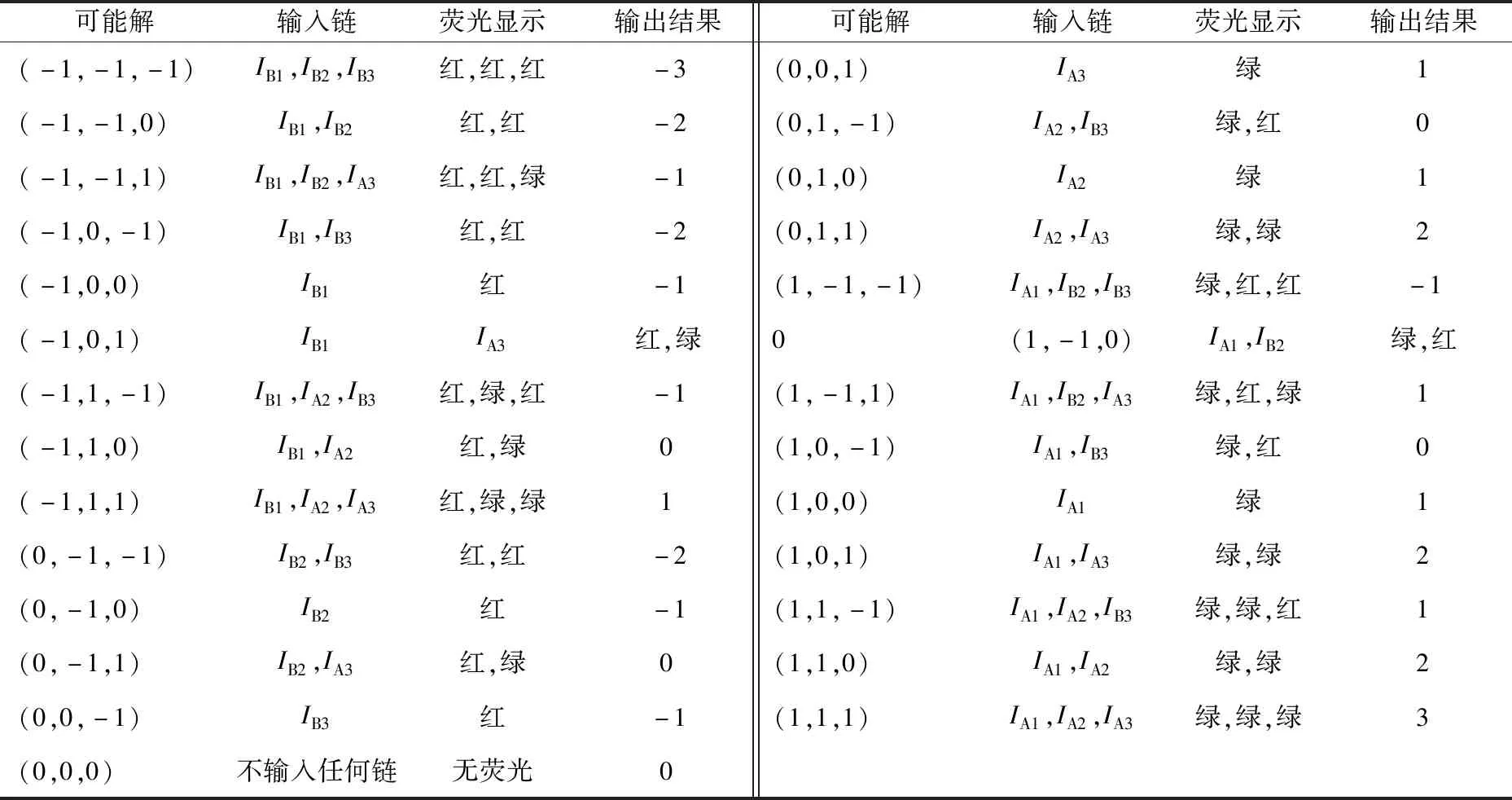
表1 27个可能解的输出结果

(3) 对于第2个约束条件x1+x3≥2,有2个变量,使用步骤(2)中设计的分子信标表示变量x1、x3以及变量x1设计的2种输入链IA1、IB1和变量x3设计的2种输入链IA3、IB3。由于第2个约束条件只含x1、x32个变量,因此只考虑这2个变量。考虑到2(0,0,1)和4(0,1,1);5(1,-1,1)、7(1,0,1)和10(1,1,1);6(1,0,0)和9(1,1,0)中x1、x3变量取值相同。因此只考虑1(-1,1,1)、2(0,0,1)、3(0,1,0)、5(1,-1,1)、6(1,0,0),取值分别为:1(-1,1)、2(0,1)、3(0,0)、5(1,1)、6(1,0)。对于解1(-1,1)向试管中加入输入链IB1、IA3,试管中出现1个红色荧光和1个绿色荧光信号,表示输出结果为0;对解2(0,1)向试管中加入输入链IA3,试管中出现1个绿色荧光信号,表示输出结果为1;对于解3(0,0)向试管中不加入任何链,即没有任何荧光信号,表示输出结果为0;对于解5(1,1)向试管中加入输入链IA1、IA3,试管中出现2个绿色荧光信号,表示输出结果为2;对于解6(1,0)向试管中加入输入链IA1,试管中出现一个绿色荧光信号,表示输出结果为1。

具体操作如图5所示。

由此可知,在满足第1个约束条件的可行解中,5(1,1)满足第2个约束条件。因此,满足前2个约束条件的可行解为:5(1,-1,1)、7(1,0,1)、10(1,1,1)。由于第3个约束条件不涉及变量x1,仅需考虑x2、x3的取值。x2、x3的取值分别为:5(-1,1)、7(0,1)、10(1,1)。继续步骤(2),结果如图6所示。

对于解5(-1,1)向试管中加入输入链IB2、IA3,试管中出现1个红色荧光和1个绿色荧光信号,表示输出结果为0;对于解7(0,1)向试管中加入输入链IA3,试管中出现1个绿色荧光信号,表示输出结果为1;对于解10(1,1)向试管中加入输入链IA2、IA3,试管中出现2个绿色荧光信号,表示输出结果为2。

(4) 第5组解(1,-1,1)和第7组解(1,0,1)是满足所有约束条件的可行解,将可行解带入目标函数并进行比较,可求得目标函数最小值为4。

3 结 论

本文利用分子信标构建了一种固定在Au表面的分子信标模型,该模型用于求解一类特殊的整数规划问题，具有传统分子信标的优点。

(1) 运算过程中没有对酶的要求,可以降低实验成本。

(2)利用荧光信号的颜色和明灭判断解的可行性,可提高检测结果的准确性和实用性。

(3) 操作简单,易于实现,比一般的计算模型更容易观察和检测问题的解。

除此之外,与传统的分子信标计算模型相比,本文设计的固定在Au表面的分子信标模型具有独特的优势。首先,利用Au表面不仅可以固定分子信标链,而且Au表面对荧光团具有猝灭能力,可以取代猝灭基团,极大程度上降低实验成本;其次,将分子信标固定在Au表面上,这种设计允许反复清洗过程;最后,之前发展的分子信标模型一般都用于溶液的检测,这种方式限制了分子信标在活体生物医学研究和生物传感中大规模的应用,而本文设计的固定在Au表面的分子信标模型,不仅可以保持分子信标原有的性质不变,而且可用于大规模的检测,大大提高了分析效率,更便于应用在疾病监测、医药检测中。进一步的工作可改进该模型使之能够应用于更一般的整数规划问题。