一种基于PCB板图像配准优化算法

任永强, 吕华鑫, 晏文彬, 李 润

(合肥工业大学 机械工程学院,安徽 合肥 230009)

图像配准作为图像处理中的一项基本问题,主要被用于求解不同传感器、不同视角、不同时间获取的图像的最佳几何变换,因此，在目标识别、图像诊断、图像拼接、缺陷检测等领域有着广泛应用[1]。其中图像特征点的提取与匹配是图像配准的关键步骤。文献[2-3]提出的SIFT特征检测算法,因对光线、尺度、平移、旋转等具有较强的适应性,从而在图像配准领域得到广泛使用;但在特征点匹配过程中,很容易产生大量的误匹配点,导致图像配准时精度较低。

目前众多学者提出了很多优化的方法。文献[4]直接使用随机抽样一致性(random sample consensus,RANSAC)算法去除外点,但在内点概率较低的情况下估计出的变换矩阵精度较低;文献[5]采用相似三角形的方法去除误匹配点对,但在外点较多时算法容易找出错误的相似三角形,因此鲁棒性较差;文献[6]使用Canny边缘算子与Harris角点结合的方法解决尺度不变特征变换(scale invariant feature transform,SIFT)特征点检测中包含大量无用点的过程,并引入均方根误差来预先删除RANSAC算法迭代过程中产生的错误匹配点,这种方式虽可靠性较高,但过程太复杂,效率较低。

为了改善PCB板缺陷检测时的图像配准精度问题,本文提出一种基于SIFT特征提取的图像配准优化方法。在SIFT算法提取特征后,先利用特征点之间的距离粗过滤去除误匹配点对;再利用改进的RANSAC算法来细过滤,得到精确的匹配点对,并求得对应的变换矩阵;最后设计误差损失函数,使用梯度下降的方法来拟合更加精确的图像变换矩阵。

实验结果表明,该方法能够有效提升PCB图像配准的精度,在PCB板缺陷检测中有着重要的实际意义。

1 图像预处理

由于相机在进行图像采集时,容易受到振动、光照等多种外部环境因素的干扰,导致图像中带有一定的噪声,为了减少噪声对后续图像处理的影响,在进行SIFT特征提取前,需要对PCB图像进行预处理。通过分析噪声的分布规律,综合比较了常用的几种滤波方法,选择中值滤波来去除PCB板常见的椒盐噪声,且该方法能够较好地保护图像的边缘特征。

为了更好地突出PCB图像经过滤波后被模糊的细节,本文通过拉普拉斯算子对图像进行锐化处理[7]。用f(x,y)表示二维图像,图像的拉普拉斯算子的公式为:

(1)

将图像进行拉普拉斯微分算子操作后,会得到该图像的突出边缘,再将原图与拉普拉斯图像进行像素值叠加。使用的计算公式为:

g(x,y)=f(x,y)+c[2f(x,y)]

(2)

其中,c为常数。

预处理后的PCB图像如图1所示。

2 图像特征检测

在实际的图像检测过程中,因为待测图像与标准图像的获取条件很难保持一致,所以对图像进行精确的定位与配准是保证后续检测算法正确执行的关键。常用的图像配准算法主要有基于图像特征、基于灰度信息、基于空间变换域的方法[8]。

考虑到本文研究的PCB板具有较为丰富的特征信息,本文使用基于SIFT特征点匹配的方法来进行图像配准。

2.1 SIFT特征点

SIFT特征点是目前最稳定的特征点,可以对光线、尺度、平移、旋转等具有较强的适应性和稳定性[9-10]。SIFT特征点的尺度不变性特征主要来源于构建图像的多尺度特征,通过对输入图像进行降采样,获得图像金字塔,并在每层图像中使用不同的高斯算子模糊,从而获取新的尺度空间序列,之后在这些序列中进行极值点判定,找出图像的特征点,这样计算机即可在不同尺度下识别该特征。

2.2 特征点方向信息与描述子

SIFT通过求取每个特征点领域内像素的梯度作为每个特征点的方向信息,其梯度方向θ(x,y)的计算公式为:

(3)

特征点梯度的模m(x,y)信息计算公式为:

m(x,y)={[L(x+1,y)-L(x-1,y)]2-

[L(x,y+1)-L(x,y-1)]2}1/2

(4)

SIFT特征描述子是通过将关键点周围16×16的采样点划分为4×4区域,再计算每个区域的梯度幅值和方向,形成一个4×4×8=128维的描述子。特征描述子如图2所示。

通过对PCB板进行SIFT特征点提取,结果如图3所示;再根据这些特征点周围信息即可得到相应的特征点描述子。

3 图像配准

变换矩阵是图像配准中的关键因素,它表示2幅图像之间的对应关系,一般用H来表示。H是一个3×3的矩阵,表示图像旋转、平移、缩放等变换。归一化后的H有8个参数,可以通过图像的特征匹配点来进行计算,每对特征点可提供2个方程来求解2个参数,因此H至少需要4对特征点对,获得精确的特征匹配点对于变换矩阵的求解至关重要[11-12]。本文提出一种改进的RANSAC算法和梯度下降相结合的方法来计算并优化图像变换矩阵。

3.1 计算初始变换矩阵

在第2节得到PCB图像的SIFT特征点后,通过特征匹配获得标准PCB图像和待检测PCB图像的匹配点对,如图4所示。

从图4可以看出,匹配中存在大量的误匹配点,这些误匹配点会对后续图像配准中的变换矩阵计算产生很大的影响。

RANSAC算法是目前广泛采用的一种去除错误匹配点的算法,其主要是从含有异常数据的样本集中计算出该样本集的数学模型参数,并获得有效的样本数据[13]。

PANSA算法的基本流程如下:

(1) 从初始匹配点集中随机抽取4对匹配特征点对计算初始的单应性矩阵H。

(2) 用H计算初始匹配点集中所有剩余的匹配点对。若某个特征点的投影误差小于预先设定的阈值,则将其划分为内点;否则标记为外点。

(3) 记下内点集合中匹配点对的数量。

(4) 重复以上步骤,直到迭代次数大于k。

(5) 将所有计算中内点数量最多的那次模型作为所要求解的单应性矩阵。

最小迭代次数k的计算公式如下:

(5)

其中:p为置信度,经验值为0.995;w为内点的概率;m为最少计算点对数目。

但是RANSAC算法在计算误匹配较多的模型参数时迭代次数变多、效率变低,且计算出的结果并非一定为最佳参数,其可信度与迭代次数成正比。

鉴于此,本文提出一种改进的RANSAC算法来提升运算效率和结果的准确性。改进算法的具体实现过程如下:

(1) 使用SIFT特征检测算法提取特征点并匹配,得到匹配点对集合S。

(2) 将步骤(1)中得到的集合S通过设置匹配点对之间的距离阈值进行初步筛选,得到筛选点集S2。

(3) 通过设置低置信度的RANSAC算法来对点集S1进行快速筛选,粗选出内点数目最多的一组点集S2。

(4) 在粗选点集S2中使用高置信度的RANSAC算法再次进行筛选,精选出内点数目最多的一组点集S3,并得出S3对应的图像变换矩阵H。

(5) 利用精选点集S3中的匹配点对,使用梯度下降的方法对变换矩阵H进行优化求解。

本文所改进的RANSAC算法的具体流程如图5所示。

改进的RANSAC算法中,第1次的低置信度的计算可以大幅降低RANSAC的迭代次数,并进一步去除误匹配点,得到准确率较高的内点集,为第2次高置信度的RANSAC算法提供更高内点概率的样本点集。相较于一开始在内点概率较低的样本集中,通过使用1次高置信度的RANSAC算法求出图像变换矩阵的方法,本文方法可以显著减少RANSAC算法的总迭代次数,减少程序运行时间,并提高结果的精确度。

3.2 优化变换矩阵

在深度学习领域里面,许多神经网络参数的学习都是通过设置一个误差损失函数并使用梯度下降的方法来进行反向传播，从而能够不断地训练模型,最终得到一个较为精确的模型参数。

本文通过上述计算,得到了强匹配特征点集S3和对应的变换矩阵H。由于H是通过S3中随机4个匹配点对求解得到的,对于S3中剩余的匹配点对可能还有些许误差。因此,本文将模仿深度学习里训练模型参数的方法,使用梯度下降来进一步获取更加精确的变换矩阵H。

首先将S3强匹配点集中待测PCB图像的特征点pi作为训练变换矩阵H的输入数据,标准PCB图像中的对应特征点qi作为标签数据,构造损失函数J(H)，即

(6)

其中:m为S3中点集的个数;d为欧氏距离。

将损失函数对H求偏导,最后使变换矩阵H沿着其梯度方向进行迭代更新,即

(7)

其中,α为超参数,用来控制H每次沿着其梯度方向迭代变化的幅值。

实验经验表明,α取0.01时可以使损失函数较快收敛,且并不会产生局部震荡的现象。

上述结果说明,本文改进方法在进行梯度下降时,可以使损失函数达到最小值并得到精度更高的图像变换矩阵H。

4 实验结果与分析

本文实验环境为:Ubuntu 16.04系统,Intel Core i7处理器,16 GiB内存(RAM),CLion 2012实验平台。使用C++编程语言,调用了OpenCV开源库和Ceres开源框架。其中:OpenCV库主要是进行图像处理方面的计算;Ceres框架集成Eigen矩阵计算库,广泛应用于求解最小二乘问题,具有很强大的算力,因此本文主要用它来进行梯度下降方面的矩阵运算。

实验图片是来自某公司实际生产线采集到的PCB板图片。通过采用多组图片在不同条件的图像配准实验来对比本文方法的效果。

在不同光照和尺度下分别使用本文方法、文献[6]算法和主流的SIFT+RANSAC算法进行图像配准实验,不同条件下的实验结果如图6～图8所示。

在标准环境下使用本文方法得到的图像变换矩阵如下:

(8)

使用文献[6]算法得到的图像变换矩阵如下:

(9)

使用SIFT+RANSAC算法得到的图像变换矩阵如下:

(10)

为验证本文方法求出的变换矩阵的准确性,本文采用均方根误差(ERMS)作为几何误差,并将其作为评价变换矩阵的精确度指标。

ERMS计算公式如下:

(11)

其中:N为所有强匹配点点数;H为变换矩阵;pi、qi分别为待测图像与标准图像中相对应的匹配特征点矢量;d为欧式距离。实验数据对比见表1所列。

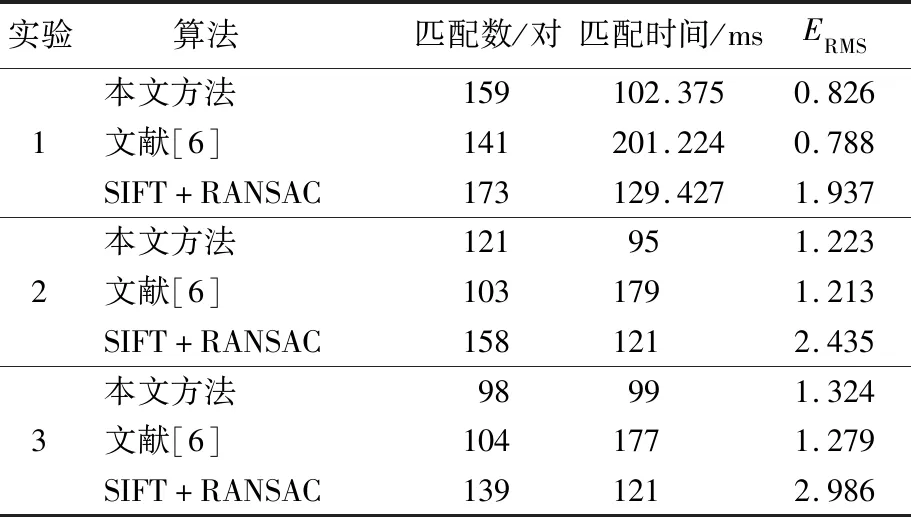
表1 实验数据对比

从表1可以看出,虽然文献[6]算法比主流SIFT+RANSAC算法得到的变换矩阵精度有了提升,但是该算法整体较为复杂,运行效率较低;本文方法在提高变换矩阵精度的同时,降低了算法运行时间,提高了执行效率,可以使PCB板图像配准更加精准迅速。

5 结 论

本文提出一种基于改进RANSAC算法和梯度下降相结合的优化方法来解决PCB板缺陷检测中的图像配准精度问题。首先使用图像预处理去除图像噪声并增强图像相关细节信息,通过SIFT特征检测提取出PCB标准版和待测板的图像特征点,利用匹配点之间的距离阈值可以初步去除误匹配点对,再通过本文改进的RANSAC算法快速获得强匹配点对以及对应的图像变换矩阵,最后使用梯度下降法进一步拟合出精确的变换矩阵。实验结果表明,本文方法能够有效提升图像变换矩阵的精度并减少运算时间。

本文方法不仅在PCB图像配准中可以应用,在一定程度上也适用于其他的图像变换场景,具有较强的实用性。