基于机器学习的进离场航空器排序优化研究

张洪杨，刘子彤，赵世豪，刘媛媛，冯晓康，张召悦

（中国民航大学，天津 300300）

终端区作为航班进离场的主要区域，其空域结构之复杂、航迹交织之密集是民航运输业发展的瓶颈所在。一般来说，在民航空域不扩张的情况下，扩大机场容量的主要方法有新建航站楼，增加跑道数量或者对进离场飞行程序进行增加和优化，重塑航班次序等，但这些方法需要大量时间和资金，多方进行沟通协调，短期内难以满足需求。相比之下，通过调整航班进离港次序的方式来提升机场容量显得更加合理高效。

终端区航班排序技术一直以来受到国内外学者的广泛关注。国内外对航空器排序算法的研究有约束位置交换算法，滑动时间窗算法和遗传算法等。Chandrasekar等依据机场跑道的运行模态、分布等提出了进离港航空器协同调度，通过分支定界法进行精确求解；Ahmed等提出了一种协同进化遗传算法，用于求解飞机航空器进离场的跑道决策与飞机排序优化的联合问题。在欧美发达国家开发了进离港辅助决策系统，例如AMAN、DMAN系统及德国的COMPAS系统。国内相较国外稍滞后，张启钱等提出基于滚动时域的遗传算法模型；张军峰等采用分支定界法对规定的时间窗内航空器进行优化仿真排序。综上，本文研究的主要内容可以概括为以下几点：介绍终端区的基本结构、根据先到先服务算法在单跑道模型上计算飞机的总延误时间、通过运用遗传算法实现单跑道模型优化的求解及将仿真算法与优化算法进行比较分析。

1 模型建立

1.1 终端区

终端区流量管理的主要措施是流量排序，机场终端区航路网络作为保障民航运输的最后一个组成部分，是保障空中交通高效运行的空中“最后一公里”。

终端区的主要结构包括进离场点、起始进近定位点、中间定位点、最后进近定位点和对应航道及机场跑道。航班穿越管制区移交点到达终端区时，要理顺航路与进近的关系，通过调整高度、速度及姿态对准进场点，当航班量过大时需要在等待区域等待进场，此时在进场排序和计量区边界的进场点就会形成等待队列，空中交通管制员也会在这个阶段为航空器进行进场排序。进场航班需汇集到同一航线上，然后依次消失高度和完成航迹的对正依次到达起始、中间进近定位点。在到达最后进近定位点之后，不再改变航班次序，按照例行程序降落在跑道上。通过对机场终端区进行网络建模，就可以知道终端区网络中各航路、各飞行程序的运行特性，有利于对机场终端区空域结构进行有效分析，做到充分高效地使用有限的终端区空域资源。

1.2 航空器进场排序模型建立

针对规划终端区飞机进场顺序，基于多架次航班单跑道降落，以总延误时间最小为目标函数，采用先到先服务算法，使用遗传算法进行求解。

假设变量：

n为划设终端区范围内需要排序的飞机总数；

i为飞机序号；

j为紧随i飞机之后的飞机序号；

ETAi为第i架飞机预计到达时间；

STAi为第i架飞机实际到达时间；

Tij为前架飞机i与后架飞机j必须保持的最小安全时间间隔；

Pi为第i架飞机；

D为总延误时间；

tj为飞机j理想着陆时间；

H为重型飞机；

M为中型飞机；

L为轻型飞机；

A为超重型飞机。

根据国际民航组织的最新规定，各型号飞机之间的尾流距离间隔（单位：km）矩阵T如下。

根据以上假设变量，建立出如下模型：将飞机的ETA（预计到达时间）、机型、呼号及飞机各个机型的尾流间隔矩阵T依次输入。假设在某一段时间，有n架飞机进入规定的飞机排序区，对这n架飞机的序列进行调整，使之在最短时间内进行降落。不考虑空中延误时间，假设飞机一架一架连续着陆，并且不同类型的飞机按照规定的尾流间隔保持安全距离，若第一架飞机未延误即STA1=ETA1，则第二架飞机的实际到达时间STA2=STA1+T12，则第二架飞机延误时间为STA2-ETA2。

根据以上假设变量，建立出如下模型：将飞机的ETA（预计到达时间）、机型、呼号及飞机各个机型的尾流间隔矩阵T依次输入。假设在某一段时间，有n架飞机进入规定的飞机排序区，对这n架飞机的序列进行调整，使之在最短时间内进行降落，且飞机i最早的降落时间为Ei，最迟降落时间为Ki。不考虑空中延误时间，STA为实际到达时间，假设飞机连续着陆，并且不同类型的飞机按照规定的尾流间隔保持安全距离，建立数学模型如下。

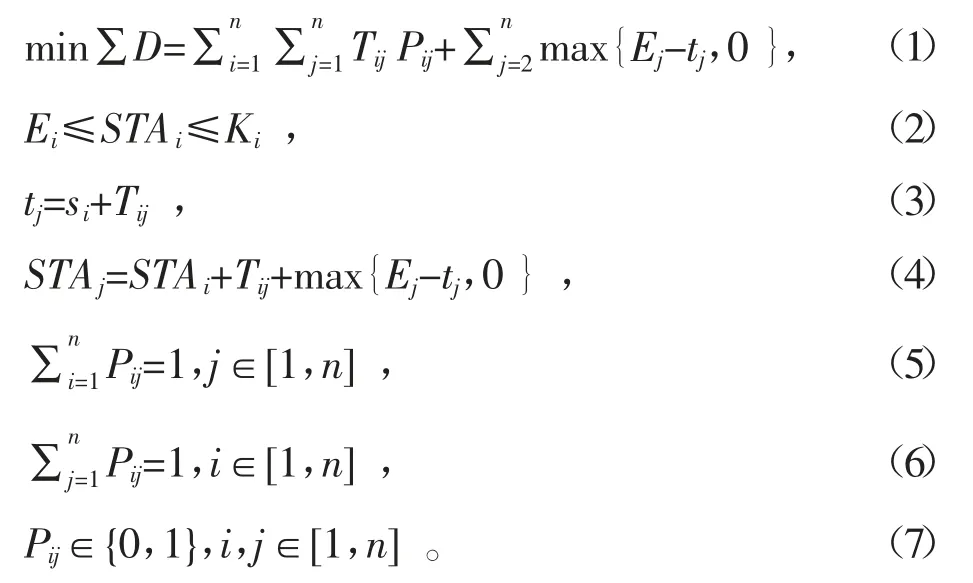
公式（2）保证排序的合理性，即实际到达时间在可接受范围内；公式（4）表示飞机实际到达时间，同时也满足尾流间隔要求；公式（5）（6）（7）代表飞机连续且存在，目标函数（1）表示求解航空器连续进离场的最小总延误时间。

2 遗传算法流程

遗传算法于20世纪70年代被提出，该算法是基于生物学上的进化、变异而提出的，其基本思想是模拟达尔文自然选择和遗传学机理中的生物进化及变异过程。在需要进行大量航班排序的情况下，传统的遍历算法耗时较长，采用遗传算法进行复杂模型运算的时候可以较快地取得较好的优化结果。其流程大致如下。

（1）初始：设置遗传代数基准时间t=0，随机生成M个个体作为初始种群P（0），并设置可接受最大遗传代数为T。

（2）种族优劣评价：计算种群P（t）中个体的适应度。

（3）选择：对群体做选择函数变换，把竞争优胜的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代，以上操作基于群体中个体的种族优劣评价。

（4）交叉：对群体做交叉函数变换。

（5）染色体变异：群体做变异算子运算。即模拟生物界染色体交叉变异可能产生优良后代，对个体的某些基因座上的数值变化。群体P（t）经过选择、交叉、染色体变异运算之后得到下一代群体P（t+1）。

（6）终止输出：当t=T，仿真结束，输出整个遗传过程中的具有最大适应度个体。

3 仿真实例分析

在本文中，采用遗传算法与先到先服务的总延误时间分别对飞机进场与离场进行对比。

3.1 单跑道飞机进场排序

进场排序运用终端区空域，建立四维坐标，根据航空器的相对位置和ETA（预计到达时间）精确时序间隔，优化排序，从而降低总体延误时间，减小终端区空域压力，如图1所示。

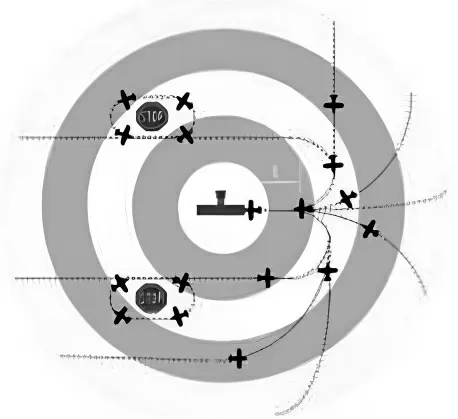
图1 终端区示意图

首先，对于单跑道飞机进行建模排序，以某个机场上空终端区为例，根据不同机型飞机在终端区的平均飞行速度，对尾流间隔（单位：s）进行时间维度的估算，得到矩阵如下。

仿真以15架飞机进行排序，表1包括飞机类型及预计到达时间。

表1 进场15架飞机名称、类型及预计到达时间

由表1可知，假定第一架飞机正点到达，不考虑飞机在空中的延误，取种群大小为200，交叉概率为0.8，变异概率为0.1，终止代数为150。得到新排序结果为：01/05/03/04/06/02/08/10/09/11/07/15/14/12/13；与采用先到先服务的排序结果进行对比，得到表2。

表2 遗传算法和先到先服务法排序结果对比

由表2可看出，遗传算法排序的总延误时间为20.7 min，平均延误时间为1.32 min；先到先服务算法排序的总延误时间为49.15 min，平均延误时间为3.28 min。所以采用遗传算法时，15架飞机队列排序总延误时间比先到先服务算法节省28.45 min，使用遗传算法后除少数飞机延误时间较长，其余飞机着陆时间均优于先到先服务排序着陆，提高运行效率。

3.2 单跑道飞机离场排序

相较于进场排序，离场排序是一个逆序推导过程。其目标是根据尾随间隔和停机位置等参数，缩小总体间隔、合理运用跑道来优化排序。航空器的离场不仅仅需要管制单位的排序，还需要与航空公司协调，更加繁杂。其主要工作流程如图2所示。

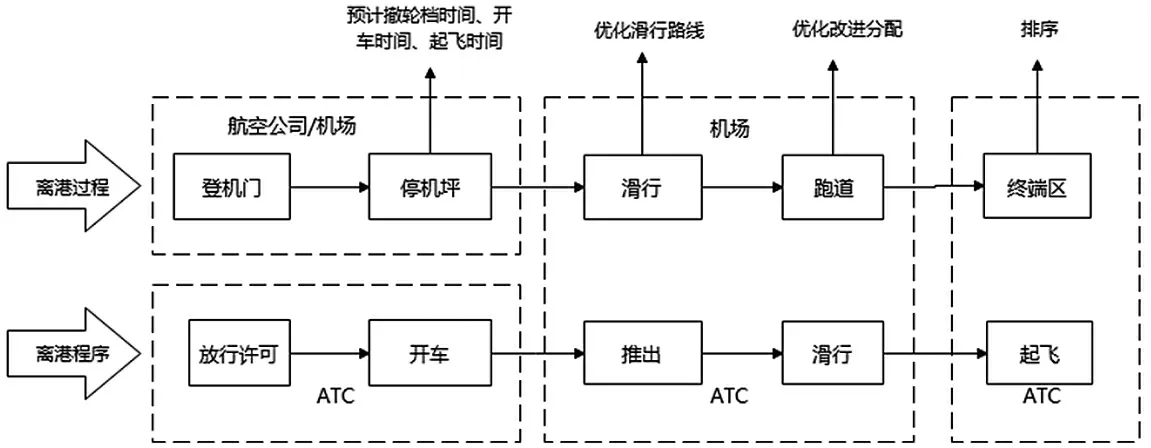
图2 离场排序工作流程

以15架航空器为例，随机分配停机位置，假设跑道运行情况良好，表3给出待起飞飞机编号预计起飞时间STD。表4给出了离场排序结果，离场排序延误时间为21.8 min。

表3 离场15架飞机名称、类型及预计到达时间

表4 离场排序结果

假设第一架飞机按时正常推出，不考虑地面等待延误，取种群大小为200交叉概率为0.8，变异概率为0.1，终止代数为150。

总延误时间为36.3 min，对应排序为13/01/02/11/08/15/04/12/09/10/03/05/14/07/06。

4 结束语

随着中国民航事业的不断发展，终端区容量已不能满足日益增加的航班流量，对终端区流量进行排序规划，调整航班进离港次序逐渐成为主流。本文通过运用遗传算法对航空器队列次序进行优化设计，以航空器总延误时间最小为目标函数，将求解结果与先到先服务算法所求结果进行对比。结果表明，通过遗传算法优化后的航空器次序优于先到先服务航空器次序，可提高航空器运行效率，从而更加有效地利用终端区空域，达到了经济、绿色和高效的管制效果。