基于分类DQN的建筑能耗预测①

李 可,傅启明,陈建平,陆 悠,王蕴哲,吴宏杰

1(苏州科技大学 电子与信息工程学院,苏州 215009)

2(苏州科技大学 江苏省建筑智慧节能重点实验室,苏州 215009)

3(苏州科技大学 建筑与城市规划学院,苏州 215009)

4(重庆工业大数据创新中心有限公司,重庆 400707)

近年来,建筑已逐渐成为全球能耗占比最高的领域[1],建筑能耗的增加不仅提升了二氧化碳的排放量,还加剧了能源危机及温室效应.因此,提升建筑能效、实现节能减排,进一步实现建筑碳中和是社会发展的重要任务.建筑能耗预测作为提升建筑能效的重要组成部分,在提高电网效率[2],改善需求响应[3],评估建筑设计方案及建筑运营策略等方面发挥着重要作用[4].

建筑能耗预测的解决方法可大致分为两类: 一类是工程方法,另一类是数据驱动方法.其中,工程方法也称白盒方法,其利用建筑传热原理和物理学方程对建筑系统进行分析建模,从而计算建筑的能源消耗[5].然而,这种方法需要详细的建筑结构信息和环境参数.一旦仿真设备参数不够准确,将会导致较高的预测误差[6].相比之下,数据驱动方法无需了解建筑内部信息,可在使用历史数据的情况下进行能耗预测.不仅如此,先前的研究已经表明,数据驱动方法可借助其解决非线性问题的能力获得优于工程方法的预测精度[7].

一般而言,数据驱动方法可分为机器学习,深度学习两类.在机器学习领域,Li 等人[8]采用支持向量机(support vector machine,SVM)构建了办公建筑冷负荷能耗预测模型,其预测结果的均方根误差和平均相对误差约为BP 神经网络(back propagation neural network,BPNN)的50%,验证了SVM 算法在能耗预测领域的优越性.Wang 等人[9]使用集成模型随机森林(random forest,RF)进行每小时的建筑能耗预测,并将其与传统的机器学习算法回归树(regression tree,RT)及支持向量回归(support vector regression,SVR)进行比较.实验结果表明,RF 可以取得更高的预测精度,具有更强的预测能力.文献[10]提出了一种基于决策树(decision tree,DT)的能耗预测模型,该方法可以准确分类并预测建筑能耗水平,同时自动排序影响建筑能耗的关键因素.与其他机器学习方法相比,该方法的竞争优势在于预测结果具备较强的可解释性.

然而,与深度学习相比,传统机器学习的特征提取能力稍显欠缺,其仅能挖掘出输入数据的浅层特征.而深度学习具有多个处理层,可将输入数据进行多次转换,获取数据内部潜藏的深层特征[11].因此,深度学习在建筑能耗预测领域受到了广泛关注.Fan 等人[12]将无监督学习提取的特征作为网络输入,而后利用深度神经网络 (deep neural networks,DNN)预测建筑冷负荷,发现可以显著提高预测精度.文献[13]则提出了一种深度递归神经网络 (recursive neural network,RNN)预测模型,以小时为单位预测办公建筑的能耗,与传统的多层感知器 (multilayer perceptron,MLP)相比,其预测的相对误差较低.

深度强化学习作为深度学习的一个重要分支,其将深度学习的感知能力与强化学习的决策能力相结合,近年来在机器人,自动驾驶等方向都获得了快速发展[14,15].而在建筑领域,深度强化学习常被用做优化控制,例如Zhang 等人[16]将深度强化学习算法用于HVAC系统控制,实现15%的供热节能.Kazmi 等人[17]则利用深度强化学习控制建筑的空间加热,并通过实验结果证明其性能优于基于规则的控制方法.但深度强化学习的能力远不止于此,它可将能耗预测建模为高维连续状态空间中的优化问题进行求解,这吸引了众多研究者的关注.Liu 等人[18]探究了深度确定性策略梯度 (deep deterministic policy gradient,DDPG)算法与异步优势行动者评论家算法(asynchronous advantage actor-critic,A3C),并将其与BPNN,RF 等算法进行比较,发现DDPG 算法建筑能耗预测精度最高.Zhang等人[19]则在DDPG 的基础上,添加了自适应早期预测方法及奖赏激励机制,进一步提高预测精度并确保算法的收敛性.但现有的研究多关注于DDPG 算法,而忽视了经典的DQN.一个可能的原因是DQN 算法只能处理离散动作空间问题.但和DDPG 相比,其优势在于可以花费更少的训练时间.

为在少于DQN 算法训练时间的情况下,取得优于DDPG 算法的预测精度,本文提出一种K-DQN 算法框架.其将深度Q 网络 (deep Q-network,DQN)算法与K 近邻 (K-nearest neighbor,KNN)分类器相结合,构建缩减动作空间进行能耗预测.具体而言,K-DQN算法将预测下一时刻的能耗转换为动作选择的形式,并针对动作空间大而导致的算法收敛慢及精度低的问题,将原始动作空间平分为多个子动作空间,并将每个子动作空间对应的状态全部划分为一类,以此训练KNN 分类器.而后在借助KNN 分类器的基础上,对不同类别相同次序的动作进行统一表示,从而将原始动作空间映射至单一子动作空间,实现对原始动作空间的缩减,使算法更易寻找最优值.此外,考虑到缩减的动作空间内每个动作具有多重含义,故将原始状态及其对应的类别概率相结合,构建出新状态作为网络输入,帮助确定动作含义并提高算法的收敛速率及预测精度.实验结果表明,K-DQN 算法在建筑能耗预测方面优于DQN、DDPG 算法,且花费更少的训练时间.

1 理论基础

1.1 深度强化学习

1.1.1 强化学习

强化学习是机器学习领域的一个重要分支,它与监督学习,无监督学习不同,其目标是最大化Agent 获得的累积折扣奖赏的期望[20].通常,强化学习问题可以被建模为马尔科夫决策过程进行求解.一个马尔科夫决策过程可以表示为一个五元组 (S,A,P,R,γ),其中S表示状态集合,A表示动作集合,P为转移函数,R为奖赏函数,γ为折扣因子.五元组可看作是Agent 与环境进行交互产生的结果.在一次交互过程中,Agent 观察到状态st,根据策略 π选择动作at,并通过转移函数P(st+1|st,at)转移到状态st+1,获得立即奖赏rt+1.此处,策略 π的具体含义为状态空间S到动作空间A的映射,P(st+1|st,at)则表示 Agent 在状态st下执行动作at,转移到下一状态st+1的概率.

Agent 的最终目标是最大化累积折扣奖赏的期望,而这一目标可通过找寻最优策略实现.策略 π可利用动作价值函数与最优动作价值函数进行评估与改进,从而产生最优策略 π*,实现最终目标.其中,动作价值函数Q表示在状态s下执行动作a的累计折扣奖赏的期望:

最优动作价值函数则表示在状态s下执行最优动作时的累计折扣奖赏的期望为:

1.1.2 深度Q 网络

传统的强化学习算法,例如Q-learning,SARSA[21,22],只能解决状态空间较小或离散的相关问题.虽然采用函数逼近等方式可以打破这一限制,但这些方法通常不够稳定,不易收敛[23].而深度Q 网络利用经验回放机制和目标网络解决了这一问题.

经验回放机制,即将Agent 与环境交互的数据样本存入经验池中,而后从经验池随机采样训练神经网络.这种方式破坏了输入数据之间的相关性,使神经网络更易收敛.其次,DQN 新构建目标Q网络用于Q网络的更新.具体而言,在网络第i次迭代时,Q网络的loss函数为:

其中,(s,a,r,s′)为一个经验池样本,目标Q网络的输出值为Q网络输出值为Q(s,a|θi).目标Q网络的引进一定程度上降低了Q值和目标Q值的相关性,提升了DQN 算法的稳定性.此外,目标Q网络的更新依赖于Q网络参数.每过J步,Q网络的所有参数将复制到目标Q网络中,完成目标Q网络的更新.

1.2 K 近邻算法

KNN 是一种基本的机器学习方法,该算法用作分类时,以样本的特征向量为输入,输出样本的类别.其基本原理如下: 对于给定的新样本,计算其与所有训练样本的距离,而后找出距离最近的K个点投票得出分类结果.K值不同,其分类的最终结果也不同.

K值选择的问题本质是一个超参数问题.选择较小K值时,算法的近似误差会降低,但估计误差会增大.同时,算法结果对近邻的样本点会非常敏感[24].一旦近邻样本为噪声,分类结果就会出错.而选择较大K值时,算法的估计误差会减少,但近似误差会增大.与样本点相关性较弱的其他样本可能也会参与投票,降低分类结果的正确性.故在实际应用中,常采用交叉验证法选择最优K值.

2 基于K-DQN 算法的能耗预测模型

2.1 K-DQN 算法的能耗预测模型

图1 展示了K-DQN 算法进行建筑能耗预测的模型框架.在数据预处理阶段,能耗数据按日期划分为训练集和测试集,并采用异常值检测方法对训练集数据进行异常值检测.同时,在考虑能耗数据日期属性及所属时刻两种因素的前提下,采用均值法对异常能耗数据进行替换.特征提取是选取一定数量的历史能耗数据作为特征的过程.可将待预测时刻的能耗当作标签,待预测时刻前的一定数量的历史能耗当作特征,对替换异常值后训练集数据进行重构,生成新的样本及标签.

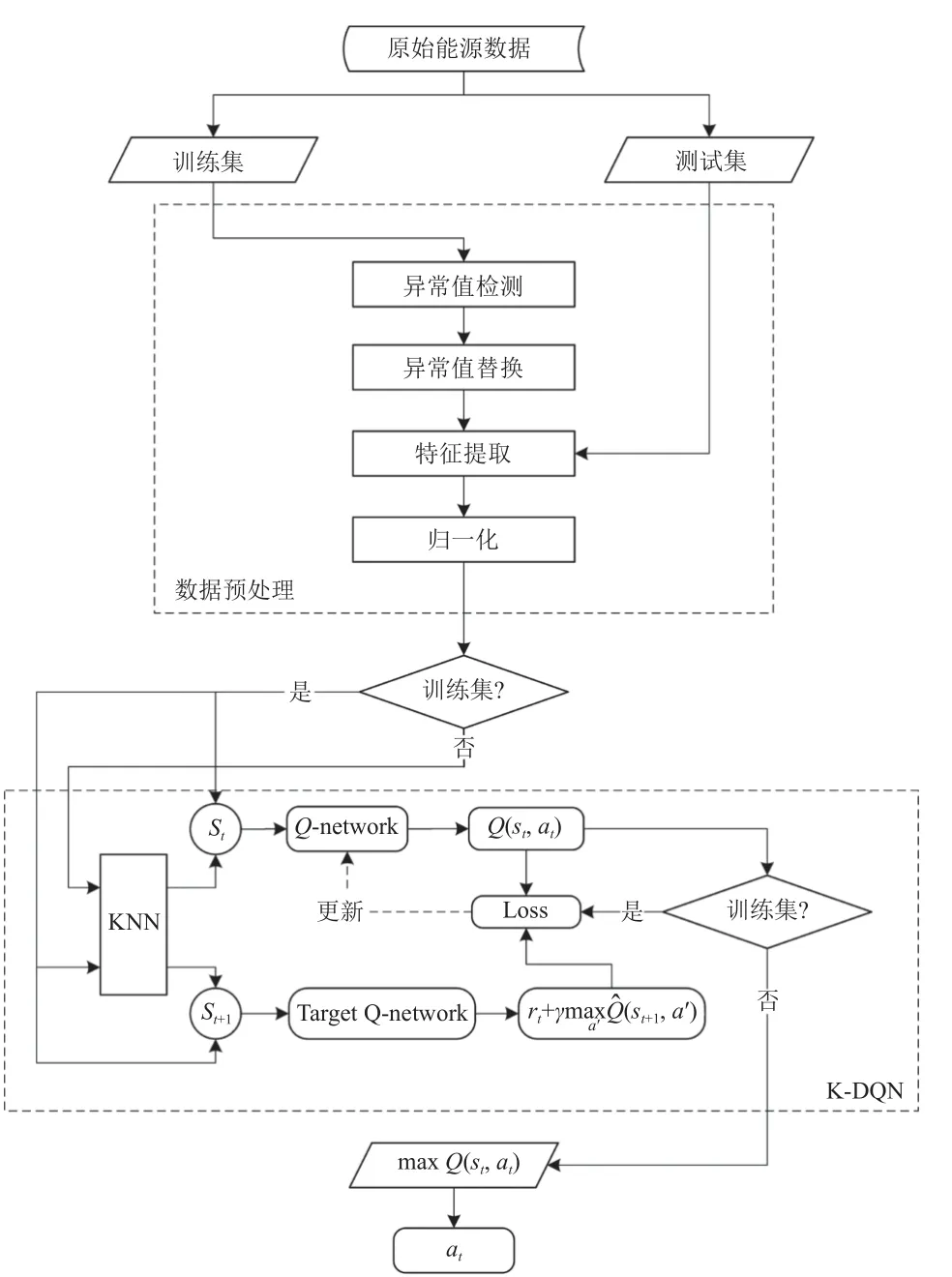
图1 K-DQN 算法能耗预测模型框架

在训练过程中,归一化后的新样本首先传入KDQN 模块中的KNN 分类器对其进行训练.待KNN 分类器训练完成后,该样本重新输入至分类器获取分类概率.此时,再将分类概率与归一化后的新样本进行合并,构建出t时刻的状态st.Q网络将st看作输入,计算动作空间下所有动作的Q值.同理,利用分类概率和归一化样本构建状态st+1传入目标Q网络,计算所有动作的目标Q值.利用目标Q值与Q值构建损失函数进行Q网络的更新.

在测试过程中,归一化后的新样本首先传入训练完成的KNN 分类器获取分类概率,而后与分类概率组成新状态传入Q网络.Q网络计算出动作空间下的所有动作的Q值,选取最优动作作为预测的能耗.

2.2 数据预处理

研究采用上海某一办公建筑能耗数据,数据采集范围为2015.1.1 至2016.12.31,采集频率为1 h/次.此外,由于2016.2.29 全天数据缺失,故总数据个数为17 520.

由于建筑内部可能存在电表混用或空调末端接入插座的现象,故需采用局部异常因子 (local outlier factor,LOF)算法和均值法对能耗数据分别进行异常值的检测和替换,以提高能耗预测的准确性.LOF是基于密度的高精度离群点检测算法[25],其计算每个样本对其邻域的局部密度偏差 (即LOF值),以发现可能的异常值.LOF值计算公式如式(4):

其中,ρk(P)表示点P的局部可达密度,即点P第k邻域内的所有点到P点的平均可达距离.Nk(P)表示点P的第k距离邻域.

直接丢弃异常数据会破坏能耗数据的时序周期性,故采用均值法进行异常值的替换.异常值的替换考虑日期和时刻两种因素.具体而言,若工作日的能耗数据存在异常,则需将前一个工作日相同时刻的正常能耗和后一个工作日相同时刻的正常能耗求和取平均,替换异常数据.若节假日的能耗数据存在异常,则利用节假日相同时刻的正常能耗进行替换.此外,研究设定训练集数据的日期范围为2015.1.1 至2016.10.31,即异常值的检测和替换操作的数据均在此日期范围,不使用测试集的任何信息.

替换异常值后的训练集数据需进行特征提取构建新样本和标签,方能传入K-DQN 模块.例如,若预测t时刻能耗,则选择t-h至t-1时刻h个历史能耗数据作为特征.此时(E～t-h,E～t-h-1,···,E～t-1)看作样本,Et看作其对应的标签.在训练集数据总数为M时,可将训练集重构为M-h个新样本和标签.同时,为了降低不同特征间的影响,提高能耗预测精度,对新样本按特征进行归一化操作:

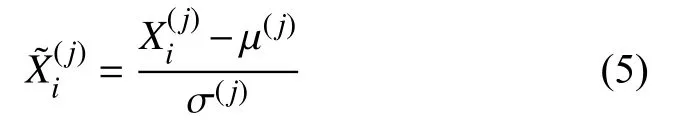
其中,和分别表示第i样本j特征的原始值和归一化值,μ(j)和σ(j)分别表示j特征的均值和方差.

2.3 MDP 建模

使用K-DQN 进行能耗预测时,需将能耗预测问题转化为MDP 过程进行求解,并对状态,动作,奖赏等进行设置.

K-DQN 算法的MDP 建模本质上是DQN 算法建模的一种改进.在使用DQN 进行能耗预测时,状态由一定数量的历史能耗数据组成,动作则根据训练集能耗数据范围进行设置.最低的能耗值可看作第一个动作,而最高的能耗值为最后一个动作.具体而言,假设历史能耗数据范围为[x,z],在步长为g的情况下,其动作空间大小为{x,x+g,x+2g,···,z},动作总个数为(zx)/g+1.

而DQN 算法的MDP 建模缺陷在于,一旦动作空间增大,动作总个数则随之增长.Q网络需计算更多动作的Q值,从而影响该算法进行能耗预测的精度和收敛速度.相比之下,K-DQN 算法采用缩减动作空间的方式进行MDP 建模,通过减少原有动作空间大小及动作总个数,提升能耗预测的精度及收敛速度.现以能耗数据范围[10,59],步长为1 为例进行说明.如图2 所示,原始动作空间X共包含50 个动作,且其内部动作值等同于Agent 预测的能耗值.实际上,原始动作空间X的动作值均可写作在某一动作值基础上进行增加的形式.转换结果如图2 中间部分,此时动作空间X转换为动作空间Y,且动作空间大小未发生改变.

图2 缩减动作空间示例

对动作空间Y而言,每行可看作一个子动作空间.若将每一子动作空间对应的状态划分为一类,则动作空间Y对应的所有状态被划分为5 类,即C0,C1,C2,C3,C4.此时,不同类别相同次序的动作可表示为:

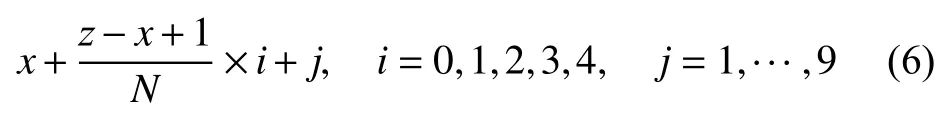
其中,N表示状态类别总个数,i表示第i类状态,j表示第j个动作,x,z为能耗数据范围的最低值10 和最高值59.由此动作空间Y可被动作空间Z替代,总动作个数由50 减少至10.更进一步考虑步长为g时的情况,此时不同类别相同次序的动作可表示为:

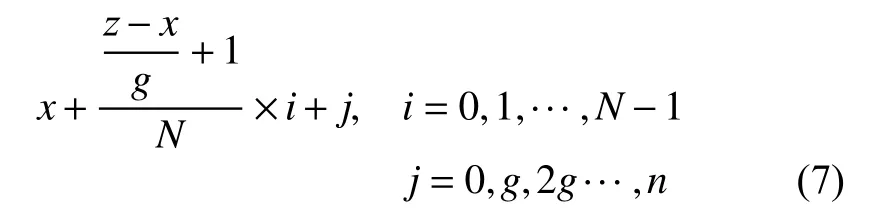
最终,N×n个总动作可减少至n,实现原始动作空间的缩减.

此外,由于缩减后的动作空间是由不同类别相同次序的动作组合而成,因此每个动作具有多重含义.例如,缩减后的动作空间第一个动作可表示每一个子动作空间的第一个动作.映射至神经网络中,则意味着一个神经元具备多种含义,这影响了Q网络的收敛速率及算法的预测精度.

为解决上述问题,我们将类别概率与归一化后的新样本进行组合,构造出状态st传入至Q网络中.在训练过程中,状态类别概率可以确定当前状态类别,从而将缩减后的动作空间映射至唯一确定的子动作空间.如图3 所示,当状态类别为C0时,缩减后的动作空间可看作是第一个子动作空间,从而确定每一动作的具体含义,提高Q网络的收敛速率及算法预测精度.

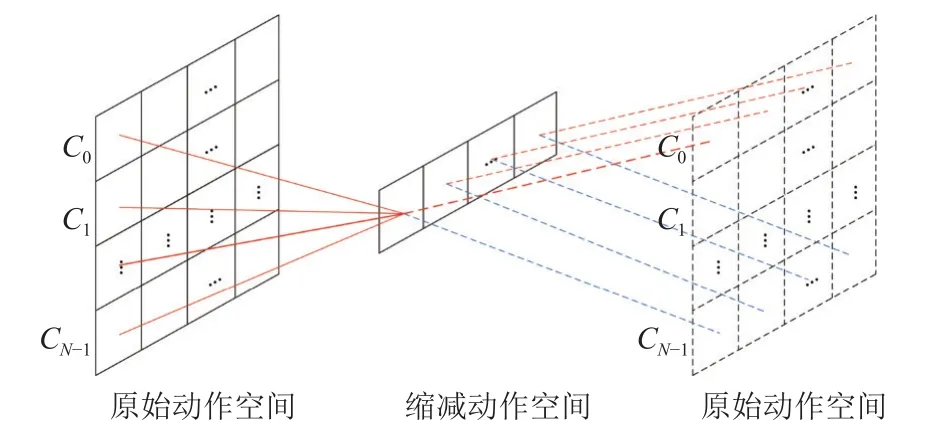
图3 缩减动作空间与原始动作空间的映射

K-DQN 算法利用缩减的动作空间进行能耗预测时,状态st由归一化样本及其对应的各类别的概率组成,表示为其中,表示归一化处理后的历史能耗数据样本,Pi表示该样本被判断为i类的概率.动作at表示Agent 在t时刻的预测能耗值,rt为t时刻Agent 获得的立即奖赏,具体表示为:

其中,Et表示t时刻的真实能耗.由式(8)可知,奖赏越接近0,Agent 预测能耗的误差越低.

2.4 K-DQN 算法流程

将能耗预测问题建模为MDP 模型后,便可利用K-DQN 算法进行建筑能耗的预测.具体来说,首先按照日期将数据集划分为训练集和测试集,并对其进行异常值的检测和替换.而后根据训练集能耗范围及设定的状态类别总数N,将原始动作空间的动作总个数缩减N倍,构建缩减的动作空间.其次,对训练集数据进行特征提取及归一化,生成新样本及标签训练KNN 分类器.

K-DQN 算法在训练时,每回合从经验池中随机选择样本作为原始状态,同时利用KNN 分类器获取该样本的各类别概率,并将二者结合构建新状态st传入Q网络.同理,构建新状态st+1传入目标Q网络.而后利用两个网络各自输出的结果,构建损失函数(yj-Q(sj,aj;θ))2更新Q网络,直至其收敛.算法1 详细描述了此训练过程.

算法1.K-DQN 算法进行能耗预测1)初始化状态类别总数D N 2)初始化经验池Q Qθθ-=θ 3)初始化 网络和目标网络 参数,4)按日期划分数据集5)对训练集数据进行异常值检测和替换6)构建缩减的动作空间7)特征提取及归一化8)训练KNN 分类器9)每一回合:10)随机选择样本11)使用KNN 分类器获取当前样本的各类别概率st 12)构建新状态13)每一步:14)在缩减的动作空间中,概率选择随机动作,概率选择1-ε max(st,a;θ)ε 15)执行所选动作获取立即奖赏st+1 rt 16)构建新状态(st,at,rt,st+1)D 17)将存入经验池(sj,a j,rj,sj+1)18)从经验池中采样19)计算y j=■■■■■■■■■rj,j+1步结束r j+γmax a′images/BZ_163_584_2354_605_2385.pngimages/BZ_163_605_2331_627_2361.pngQ(sj+1,a′|θ-),否则(y j-Q(sj,a j;θ))2Q 20)利用更新 网络JˆQ=Q 21)每步设置22)23)Until 最终状态 or 最大步数24)Until 最大回合数st←st+1

3 实验仿真

在本节中,我们将采用DQN,K-DQN,DDPG 算法进行建筑能耗预测的分析与比较.第4.1 节描述了3 种算法的基本实验设置.第4.2 节选取了3 种评价指标比较不同算法的预测结果.第4.3 节从预测精度,收敛速率,训练时间3 个角度分析3 种算法的优劣.

3.1 基本实验设置

在特征提取阶段,实验采用前24 个时刻历史能耗数据作为特征,预测下一时刻的能耗.由此3 种算法的超参数设置如下: DQN,DDPG 算法输入层神经元个数为24,K-DQN 输入层神经元个数为 24+N(N为状态类别总数).此外,由于训练集能耗数据范围为 [24,2703],故DQN,K-DQN 算法采用步长为1 的方式,将连续动作空间转换为离散动作空间进行能耗的预测.同时,为保证算法比较的公平性,3 种算法均使用相同学习率及相同网络架构.对输出层而言,DQN,K-DQN 算法的输出层神经元个数取决于动作总个数,而DDPG 算法由于自身处理连续问题的性质,需将其设置为1.表1详细列举了3 种算法所使用的超参数.

表1 超参数设置

此外,由于K-DQN 算法内部使用KNN 分类器,且K值选择问题是超参数问题,故实验采用6 折交叉验证选取最优K值.

3.2 评价指标

为比较3 种算法的预测精度,选取平均绝对误差(mean absolute error,MAE),均方根误差 (root mean square error,RMSE),决定系数(coefficient of determination),作为评价指标.其计算公式分别为:

其中,m表示样本总个数,yi和y′i表示第i样本的真实值及预测值,为整体样本的均值.

3.3 结果与分析

研究使用的实验结果均建立在表1 超参数设置的基础上,且为降低训练过程中其他随机因素的影响,每一实验结果都取自10 次实验结果的平均值.

图4 展示了DQN,DDPG 以及不同类别总数情况下K-DQN 算法的整体预测情况.其中,横轴表示算法的预测能耗值,纵轴表示真实能耗.蓝色实线为经过原点的斜率为1 的直线,代表预测值和真实能耗值相同.故图像中的散点越靠近该直线,则说明算法的预测精度越高.此外,蓝色虚线是20%的误差线,靠近纵轴的蓝色虚线意味着预测能耗值是真实能耗值80%,靠近横轴的蓝色虚线则表示预测能耗值是真实能耗的120%.二者组成的阴影部分为预测值和真实值相差20% 的误差带.从这个角度看,DQN 算法在真实能耗值低于500 时有较多的预测点处于误差带之外,说明预测精度较差.相比之下,DDPG 算法的预测结果整体偏向于左上方,说明该算法的整体预测值均偏小.对KDQN 算法而言,由于其算法内部使用KNN 分类器对状态进行了划分,故预测出的能耗点呈现出一定的分类趋势.例如状态类别总数为6 和8 的K-DQN 中,有较为明显的簇.

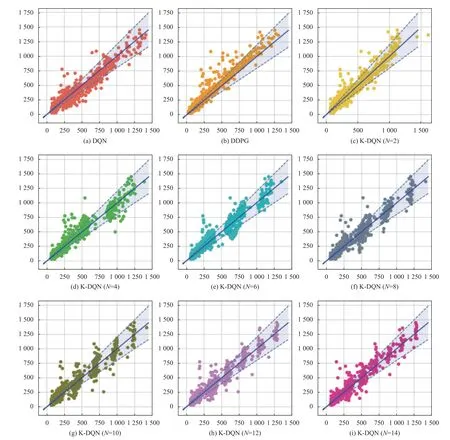
图4 3 种算法预测结果 (其中,横坐标表示算法的预测能耗值 (kWh),纵坐标表示真实能耗 (kWh))

表1 和表2 描述了3 种算法的具体预测精度.从MAE角度看,DQN 算法预测精度最低,为51.566,而状态类别总数为7 的K-DQN 算法预测精度最高,其MAE值为39.852.DDPG 与状态类别总数为14 的KDQN 算法预测精度相近,其预测结果的MAE值均为44 以上.在比较RMSE指标的情况下,不同类别总数的K-DQN 预测精度均高于DQN,DDPG 算法,其整体RMSE值处于70 以下.类别总数为3 时的K-DQN是个特例,其原因可能是测试过程中KNN 分类器对新样本分类错误导致.R2指标反映了算法模型的拟合精度,越靠近1 则说明算法的预测精度越高.由表1、表2 可知,K-DQN 算法的预测精度均高于DQN、DDPG 算法,且类别数为6、7 的K-DQN 算法预测精度最高.

此外,对K-DQN 算法而言,类别数越多,动作空间总动作个数越低,算法的预测精度越高.但由于其内部分类器的分类准确率会随类别数的增加而逐渐降低,从而影响算法预测精度,故表3 中K-DQN 的预测精度整体呈先上升后下降的趋势.综合来看,类别总数为7 的K-DQN 模型效果最优,预测精度最高.

图5 展现了3 种算法训练过程中的MAE变化趋势.其中,DQN 算法的收敛速度最次,且收敛后的MAE值高于DDPG 及K-DQN 算法.此外,由于DQN及N=2 时的K-DQN 算法起始MAE值较高,以致图5不易比较分析DDPG 及其他分类总数下的K-DQN 算法.故将二者去除,生成图6.图6 由第3 回合开始进行展示,可以看出DDPG 算法与类别总数为8 的K-DQN算法收敛趋势相近,但收敛后的MAE值略高.对KDQN 算法而言,KNN 分类使得K-DQN 具有较低的MAE初始值,且状态类别数越多,K-DQN 算法收敛速率越快,收敛后的MAE值越低.故该实验中,类别总数为14 的K-DQN 算法收敛速率最快.

图5 3 种算法的MAE 变化趋势

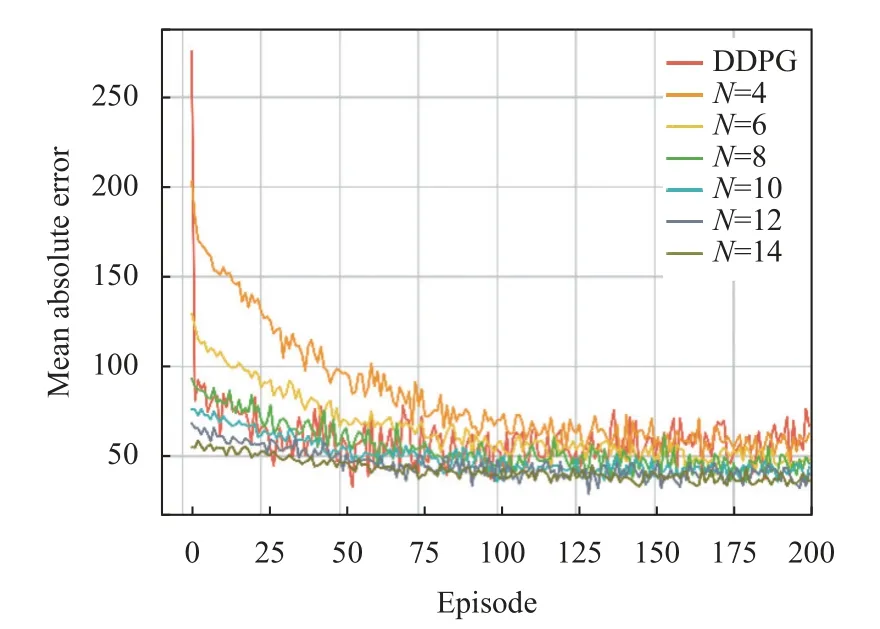
图6 3 种算法的MAE 变化趋势 (从第3 回合开始)

表2 和表3 同时展示了3 种算法的训练时间.其中,DDPG 算法的训练时间最长,为1 353.058 s.DQN算法训练时间其次,为1 190.733 s.而K-DQN 算法的训练时间则取决于状态类别总数.一般而言,状态类别总数越多,动作空间越小,网络训练所需的参数越少,训练时间越低,故K-DQN 算法的训练时间随类别数增加整体呈下降趋势.但由于实验过程中随机因素无法完全消除,以致于出现个别偏差值,例如类别数为10 时的K-DQN 算法情况.

表2 DQN 和DDPG 算法的预测精度及训练时间

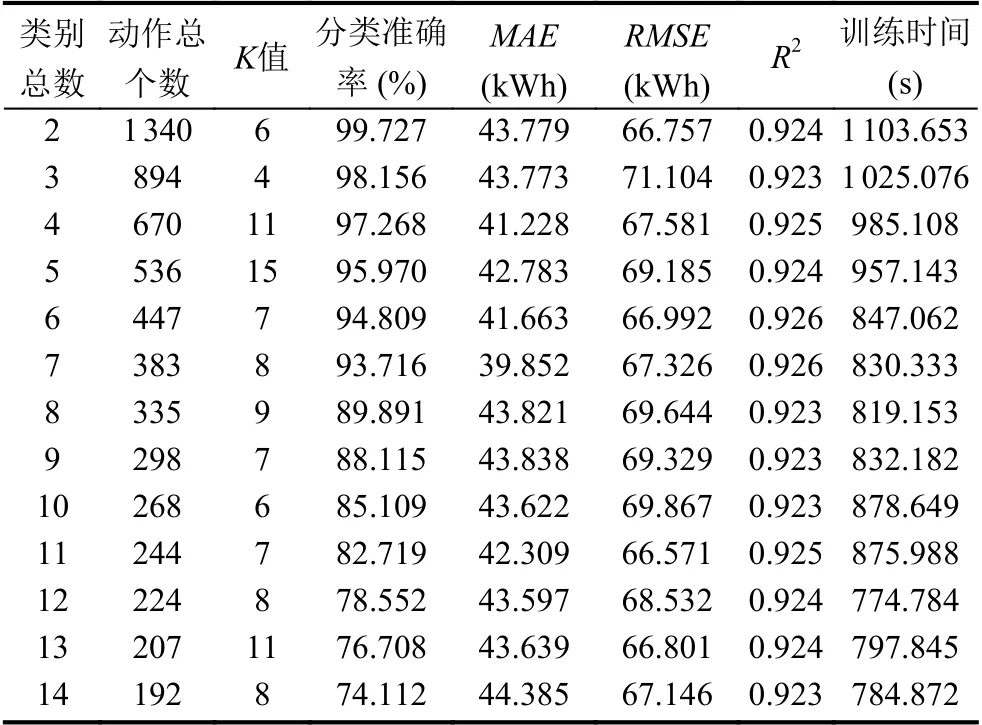
表3 K-DQN 算法的预测精度及训练时间

4 结论与展望

K-DQN 是一种将KNN 分类器与DQN 相融合的算法框架,可在减少网络训练时间的情况下,获得优于DQN、DDPG 算法的建筑能耗预测精度.该算法首先对原始动作空间进行平均划分,产生多个子动作空间,而后将每个子动作空间视作一类训练KNN 分类器.并在此基础上,对不同类别相同次序的动作进行统一表示,从而将原始动作空间映射至单一子动作空间中,实现原始动作空间的缩减.缩减后的动作空间与原始动作空间相比,动作个数更少,算法更易寻找最优值,进而提升建筑能耗预测的精度.此外,K-DQN 算法将历史能耗数据及其对应的分类概率组合构建为 Q 网络的输入,确定了单一动作在网络中的具体含义,提高了算法的收敛速率及预测精度.最终的实验结果证明,与DQN,DDPG 算法相比,类别为7 的K-DQN 算法在预测精度,收敛速率,训练时间方面均取得更优结果,验

证了K-DQN 算法的有效性.此外,由于K-DQN 算法的本质是缩减动作空间,故在建筑能耗范围较大时,算法特性会发挥得更加明显.在后续工作中将对这一特性进行讨论说明,提升K-DQN 算法框架的通用性.