区间多阶段双侧随机联合概率机会约束规划模型
——以民勤县红崖山灌区水资源优化配置为例
边乐康 张成龙 郭 萍 潘 琦
(中国农业大学 水利与土木工程学院,北京 100083)
目前,全球水资源短缺形势日益突出,2020年我国人均综合用水量仅为412 m,农业用水占总用水量超过60%。我国西北干旱地区,90%的水资源用于农业灌溉,水资源与土地资源之间的关系更为密切。因此,在水资源有限的前提下,对农业水资源进行优化配置是实现水资源可持续发展的必要措施。
水资源优化配置模型可以实现水资源利用的科学化和土地灌溉面积分配的合理化。已有研究结合不同方法进行水资源优化配置:结合区间参数规划(Interval parameter programming, IPP)方法和多阶段随机规划(Multi-stage stochastic programming, MSP)方法的区间多阶段随机规划方法(Interval multi-stage stochastic programming, IMSP)可以解决以区间形式存在参数的不确定性,并且描述系统的动态变化过程。例如,付强等将区间多阶段随机规划模型应用于灌区多水源优化配置,引入水分敏感指数权重系数,实现了灌区多水源系统灌溉的动态配水;Zhang等建立区间多阶段多目标随机规划模型及相应的求解方法,通过应用于黑河流域中游地区的灌溉水分配案例中证实模型有效性。但是,对于约束过程中的随机不确定性,在上述方法中并不能得到很好的解决。当约束条件双侧的参数存在不确定性且约束存在一定的违规风险时,可以引进机会约束规划(Chance-constrained programming, CCP)方法解决。系统约束在一定的违规风险的情况下,决策变量可以获得更大的优化结果,多阶段之间的动态变化过程导致它们之间的违规概率水平存在一定的相依关系,因此研究多阶段的联合概率关系和独立概率互动具有一定意义,可以考虑在模型中引入联合概率规划(Joint-probabilistic programming, JPP)方法反映不同时段违规风险水平的联动效应。例如,Zhang等构建应用于黑河中游作物灌溉面积动态规划的区间多阶段左手边随机联合机会约束规划模型,很好的解决了以区间形式存在的不确定性参数及部分随机不确定性参数。
本研究结合区间多阶段随机规划与双侧随机机会约束规划,同时引入联合概率规划,拟构建区间多阶段双侧随机联合概率机会约束规划模型,并应用于民勤县红崖山灌区。模型应用时以灌区地表水可利用水量的预测为基础进行水资源优化配置,以期为决策者提供不同违规概率情况下的决策方案。
1 模型建立
1.1 区间多阶段随机规划模型
在水资源优化配置过程中,将区间数学规划与随机数学规划结合起来可以形成诸如区间两阶段随机规划和区间多阶段随机规划等方法。对于区间多阶段随机规划,如果预先给定的可利用水量能够满足用水需求,则会带来经济效益;反之,如果预先给定的可利用水量不能满足用水需求,则会带来相应的经济惩罚。一般的IMSP模型形式如下:
(1)
s.t.
i
=1,2,…,I
;t
=1,2,…,T
式中:f
为规划期内的目标函数;±表示区间值;i
为用水单元,共有I
个用水单元;t
为研究时段,共有T
个研究时段;为预先给定的用水单元i
在时段t
的灌溉目标;和为最大和最小的灌溉目标;为用水单元i
在t
时段内的灌溉效益;为用水单元i
在t
时段内的惩罚系数;K
为每个时段的情景数;p
为每种情景出现的概率;为用水单元i
在t
时段k
情景下带来缺水惩罚的缺水量;为指时段t
在情景k
时的可利用水量;和为上一时段盈余或者匮缺的水量。1.2 双侧随机联合概率机会约束规划模型
双侧随机机会约束规划(Double-sided stochastic chance-constrained programming, DSCCP)可以处理约束双侧随机不确定性问题。同时,模型引入的联合概率规划JPP可以反映在不同联合违规概率和不同独立违规概率下的优化结果。二者结合的双侧随机联合概率机会约束规划(Double-sided stochastic joint-probabilistic chance-constrained programming, DSJCP)的一般形式如下:
(2)
s.t.
(3)
x
≥0j
=1,2,…,m
i
=1,2,…,I
式中:f
为线性目标函数;x
为实数决策变量;c
为实数参数;a
,b
分别为约束双侧的随机变量,服从随机正态分布;μ
为均值;σ
为标准差;p
为j
阶段机会约束的独立违规概率,共有m
个阶段;1-p
为j
阶段给定的约束满足程度;p
为联合概率,即所有机会约束给定的违规概率之和。对于约束双侧存在独立正态分布变量的式(3),为便于计算,需要将该约束条件进行线性化。根据Zhang等的研究,式(3)可以转化为非等价但有效的式(4):
(4)
式中:Φ(1-p
)为随机变量1-p
的概率密度函数,Φ(1-p
)为Φ(1-p
)的逆函数。1.3 区间多阶段双侧随机联合概率机会约束规划模型
为解决模型中参数的不确定性问题并反映不同违规风险下的优化结果,本研究结合IMSP模型和DSJCP模型,建立了区间多阶段双侧随机联合概率机会约束规划模型(Interval multi-stage double-sided stochastic joint-probabilistic chance-constrained prog-ramming, IMDSJCP),一般形式如下:
(5)
s.t.
1-p
(k
=1,2,…,K
)(6)
1-p
(k
=1,2,…,K
-1)(7)
x
≥0其中:i
=1,2,…,I
;t
=1,2,…,T
;j
=1,2,…,m
根据1.2部分提及到的线性化方法,当p
≤0,x
≥0时,将式(6)和(7)进行等效线性化:(8)
其中:t
=1,2,…,T
;k
=1,2,…,K
;j
=1,2,…,m
(9)
其中:t
=1,2,…,T
;k
=1,2,…,K
。2 实例应用
2.1 研究区域
民勤县为甘肃省武威市下辖县,位于石羊河流域下游,其地理位置处于东经101°49′41″~104°12′10″、北纬38°3′45″~39°27′37″,夏季平均气温约22.8 ℃,冬季平均气温为-9.9 ℃,且昼夜温差较大;年均相对湿度为50%,年均降水量100 mm,年均蒸发量2 485.8 mm(20 cm蒸发皿)。降水稀少且蒸发量大,属于典型的大陆性沙漠气候。
石羊河干流经过蔡旗镇汇入红崖山水库,最终流入民勤县。位于蔡旗镇的蔡旗断面的地表水与环河灌区(纯井灌区)地下水部分交换后,会在红崖山水库蓄积,其是民勤盆地的主要地表水来源,用以调节农业灌溉,因此设立于蔡旗镇的蔡旗水文站是监控流入民勤县境内水量的控制断面。民勤县的红崖山灌区南接红崖山水库,是民勤县境内面积最大的灌区,同时也是重要的粮食和农产品基地,主要经济收入来源于土地种植,主要种植粮食作物有小麦、玉米,主要种植经济作物有蔬菜和瓜果等,灌区的人口、粮食产量及农业总收入均占全县前列。红崖山灌区灌溉以地表水为主、地下水为辅,其地表水可供水量由红崖山水库提供。根据多年的观测资料分析,蔡旗断面到红崖山水库出库断面之间的输水效率约为0.89,因此可以构想基于对蔡旗断面径流量的预测来实现对红崖山灌区进行水资源优化配置。在此案例中,只考虑地表水灌溉,将地下水灌溉和由于水资源不足而引发的外调水共同视为带来缺水惩罚的部分。图1示出研究区域概况图。
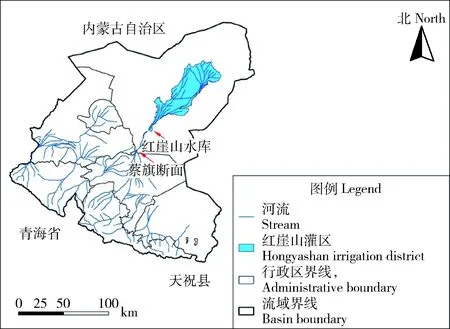
图1 研究区域概况图Fig.1 Research area map
2.2 模型应用
本研究选取石羊河流域的红崖山灌区为研究区域,用i
表示用水单元,即研究作物,选取灌区粮食作物、蔬菜和瓜果类(瓜果、坚果、饮料及香料)经济作物为研究作物;选取2021—2025年、2026—2030年、2031—2035年作为研究时段(t
),分别表示为t
=1,2,3;假设应用过程共有3种流量水平,L表示低流量水平,M表示中流量水平,H表示高流量水平,3种流量水平出现概率分别为0.2,0.6,0.2;用K
表示每个时段流量水平,每个时段有3种流量水平,则在第二时段有9种流量水平,第三时段有27种流量水平,即t
=1时,K
=3(L,M,H);t
=2时,K
=9(LL,LM,LH,ML,MM,MH,HL,HM,HH);t
=3时,K
=27(LLL,LLM,LLH,LML,LMM,LMH,LHL,LHM,LHH,MLL,MLM,MLH,MML,MMM,MMH,MHL,MHM,MHH,HLL,HLM,HLH,HML,HMM,HMH,HHL,HHM,HHH),流量水平设置示意图见图2。模型求解所需数据参考《武威市统计年鉴》(2016—2020年)、《民勤县人民政府关于印发民勤县国民经济和社会发展第十四个五年规划和二〇三五年远景目标纲要的通知》、《武威市国民经济和社会发展第十四个五年规划和二〇三五年远景目标纲要》和调研获得的研究区域内部资料。不同情景下蔡旗断面径流量及出现概率根据桂泽瑛研究结果获得,取值见表1、表2和表3,应用过程中的其他基础数据见表4。
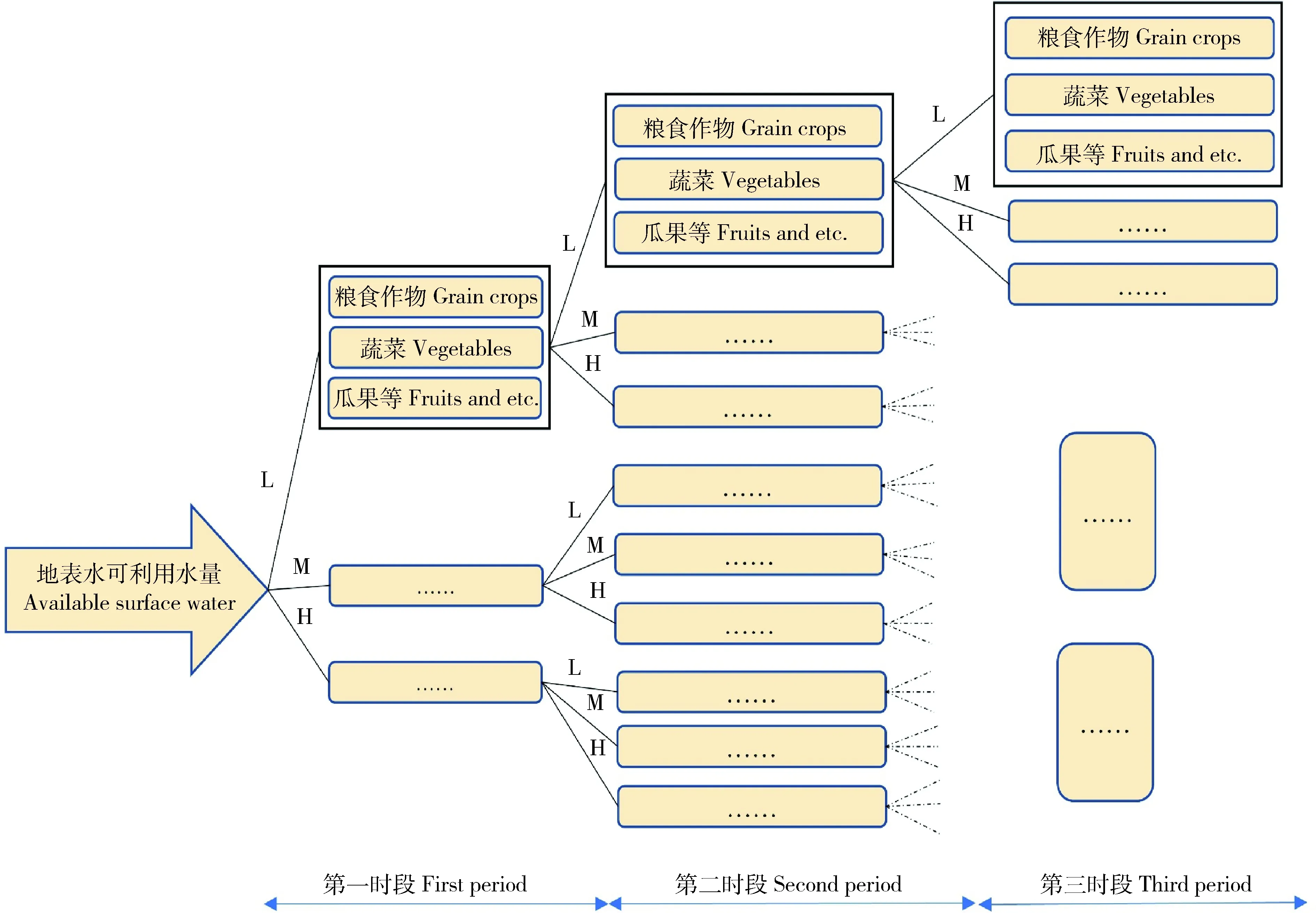
L、M和H分别表示低流量水平、中流量水平和高流量水平。表1, 表2和表3同。 L represents low flow level. M represents medium flow level. H represents high flow level. Same asTables 1, 2 and 3.图2 模型应用过程中的多阶段情景数示意图Fig.2 Diagram of multi-stage scenario number in model application
表1 第一时段(=1)蔡旗断面径流量及出现概率
Table 1 Predicted runoff of Caiqi section and occurrence probability for the first period
流量水平Flow level径流量/(106 m3)Runoff概率ProbabilityL[225.90,308.20]0.2M[253.33,335.64]0.6H[280.77,363.07]0.2
注:=1为第一时段,2021—2025年。表4和表5同。
Note: =1 is the first period, 2021—2025. Same as
Tables 4 and 5.
表2 第二时段(=2)的蔡旗断面径流量及出现概率
Table 2 Predicted runoff of Caiqi section and occurrence probability for the second period
流量水平Flow level径流量/(106 m3)Runoff概率Probability流量水平Flow level径流量/(106 m3)Runoff概率ProbabilityLL[240.97,323.27]0.04MH[295.84,378.14]0.12LM[268.40,350.71]0.12HL[240.97,323.27]0.04LH[295.84,378.14]0.04HM[268.40,350.71]0.12ML[240.97,323.27]0.12HH[295.84,378.14]0.04MM[268.40,350.71]0.36
注:=2为第二时段,2026—2030年。表4和表5同。
Note: =2 is the second period, 2026-2030. Same as
Tables 4 and 5.
表3 第三时段(=3)的蔡旗断面径流量及出现概率
Table 3 Predicted runoff of Caiqi section and occurrence probability for the third period
流量水平Flow level径流量/(106 m3)Runoff概率Probability流量水平Flow level径流量/(106 m3)Runoff概率ProbabilityLLL[256.04,338.34]0.008MMH[310.91,393.21]0.072LLM[283.47,365.78]0.024MHL[256.04,338.34]0.024LLH[310.91,393.21]0.008MHM[283.47,365.78]0.072LML[256.04,338.34]0.024MHH[310.91,393.21]0.024LMM[283.47,365.78]0.072HLL[256.04,338.34]0.008LMH[310.91,393.21]0.024HLM[283.47,365.78]0.024LHL[256.04,338.34]0.008HLH[310.91,393.21]0.008LHM[283.47,365.78]0.024HML[256.04,338.34]0.024LHH[310.91,393.21]0.008HMM[283.47,365.78]0.072MLL[256.04,338.34]0.024HMH[310.91,393.21]0.024MLM[283.47,365.78]0.072HHL[256.04,338.34]0.008MLH[310.91,393.21]0.024HHM[283.47,365.78]0.024MML[256.04,338.34]0.072HHH[310.91,393.21]0.008MMM[283.47,365.78]0.216
注:=3为第三时段,2031—2035年。表4和表5同。
Note: =3 is the third period, 2031—2035. Same as
Tables 4 and 5.
2
.2
.1
目标函数(10)
式中:为预先给定的红崖山灌区i
作物t
时段的灌溉面积,为红崖山灌区i
作物t
时段单位面积的净效益,10元/hm;p
为t
时段k
情景出现的概率,每个时段各个情景的概率和为为红崖山灌区i
作物t
时段由于不用地表水灌溉而带来的单位面积经济惩罚,10元为决策变量,即红崖山灌区i
作物t
时段在情景k
下的地表水灌溉面积,hm。当t
分别取1, 2, 3时,目标函数可改写为:(11)
表4 3个阶段的研究作物灌溉定额和地表水用于农业灌溉的比例
Table 4 The irrigation quota of crops and the proportion of surface water for agricultural irrigation in three stages
参数Parameter指标Index作物种类Crop species研究时段 Study periodt=1t=2t=3灌溉定额Irrigating quota均值/(m3/hm2)标准差/(m3/hm2)粮食作物6 9456 8106 810蔬菜 6 6456 6456 645瓜果等 6 2406 2406 240粮食作物481481481蔬菜 537537537瓜果等 537537537地表水用于农业灌溉的比例Proportion of surfacewater for agriculturalirrigation均值标准差粮食作物0.570.570.57蔬菜 0.570.570.57瓜果等 0.570.570.57粮食作物0.016 30.016 30.016 3蔬菜 0.016 30.016 30.016 3瓜果等 0.016 30.016 30.016 3
2
.2
.2
约束条件1)地表水可供水量约束:地表水灌溉所用的全部地表水要小于等于地表水用于农业灌溉的水量。同时前一阶段盈余或者亏缺的水量会影响下一阶段的可用水量,形成一个动态规划过程。
1-p
(t
=1;k
=1,2,3)1-p
(t
=2;k
=1,2,…,9)1-p
(t
=3;k
=1,2,…,27)1-p
(t
=1;k
=1,2,3)1-p
(t
=2;k
=1,2,…,9)式中:K
为蔡旗断面到红崖山水库出库断面之间的输水效率,本研究取K
=0.89; iq为红崖山灌区i
作物t
时段灌溉定额,m/hm,假设服从正态分布为t
时段k
情景时的地表水预测量,分别为时段t
和时段(t
-1)在情景k
对应的地表供水量的盈余或亏缺水量,10m;β
为地表水用于农业灌溉的比例,假设服从正态分布2)联合概率约束:
式中:p
为联合违规概率,反映3个时段之间的关联,采用联合概率违规约束;p
为t
时段的独立违规概率。3)种植(灌溉)面积约束:根据红崖山灌区续建配套与现代化改造实施方案,红崖山灌区的经粮比和第二类作物与第三类作物的比值均限制在一定范围内。
式中:FC,FC为粮经比的最小比例与最大比例,3个阶段相同,本研究取0.55和0.61;VC,VC分别为i
与i
作物比值的最小比例与最大比例,本研究取0.37和0.45。4)灌溉需求:地表水和地下水联合配置量必须大于最小灌溉需求,以保证作物最小产量。
(t
=1,k
=1,2,3)(t
=2,k
=1,2,…,9)(t
=3,k
=1,2,…,27)式中:TWBmin为作物最小灌溉需水量的地表水参与灌溉量,m,第一和第二阶段取10 003.8万m,第三阶段取10 371万m。
5)非负约束:
根据交互式算法对模型进行求解,根据上下限子模型求解所得的结果得出最终区间解。
2.3 结果分析
本案例设置3个连续增加的联合违规概率0.01,0.05和0.1,联合违规概率的递增表示决策者的决策风险在增加。同时为了更深入的研究不同阶段在不同违规概率情况下的优化结果,每个阶段划分3种独立违规概率变化趋势,并据此设置3种情景:
1)A情景,3个阶段的独立违规概率相同,即3个时段的约束违规风险程度相同;
2)B情景,3个阶段的独立违规概率递增,即3个时段的约束违规风险程度依次增加;
3)C情景,3个阶段的独立违规概率递减,即3个时段的约束违规风险程度依次减少。
同时,本案例通过设置1A,1B,1C,2A,2B,2C,3A,3B,3C共9种分析情景分析不同联合违规概率与独立违规概率组合情况下的优化结果。A,B,C字母之前的系数1,2,3分别表示3个递增的联合违规概率。区间多阶段双侧随机联合概率机会约束规划模型可以展现在不同约束违规概率的情况下灌溉目标、灌溉方案和灌溉效益的变化。
2
.3
.1
灌溉目标使用LINGO软件求解过程中,引入决策变量Z
,Z
∈[0,1],使则作物的灌溉目标可以根据Z
权衡。当Z
取1时,表示决策者对i
作物在t
时段的灌溉面积持有积极的态度,决策者会根据种植更大的作物面积来获取更大的灌溉效益,但是也同时会带来更大的经济惩罚;相反地,当Z
取0时,表示决策者对i
作物在t
时段的灌溉面积持有保守的态度,同时会获得较低的灌溉效益和经济惩罚。模型通过求解得到作物优化灌溉目标(表5)。可见,对于粮食作物,在9种情景下Z
值会有变化,这表明粮食作物对于违规概率和独立概率的改变较为敏感,而且粮食作物的用水竞争性低于经济作物。例如,在2A情景下,粮食作物在3个时段的Z
值分别为0,0.27,0.98,这表明在灌溉过程中优先灌溉经济作物会获得更大的灌溉效益,同时随着上一个时段盈余水量的增加,粮食作物的灌溉面积也越来越大。对于经济作物,蔬菜和瓜果等作物在3个时段的Z
值均取1,这表明决策者为了获取更高的灌溉效益,会对经济作物的种植保持积极的态度。表5 9种情景下研究作物的优化灌溉目标
Table 5 Optimized irrigation objectives of crops under nine scenarios
情景Scenario粮食作物 Grain crops蔬菜 Vegetables瓜果等 Fruits and etc.t=1t=2t=3t=1t=2t=3t=1t=2t=31A000.681111111B000.981111111C000.331111112A00.270.981111112B00.340.981111112C000.981111113A00.840.981111113B00.830.981111113C00.670.98111111
注:A,B,C分别表示独立违规概率在3个阶段不变、递增和递减的情景,字母前面的系数分别表示3个递增的独立违规概率。下表、图同。
Note: A, B and C respectively denote the scenarios in which the individual violation probability is constant, increasing and decreasing in three stages, and the coefficients in front of the letter represent three increasing individual violation probabilities. Same as the following
Tables and Figs.
2
.3
.2
灌溉方案不同情景下的优化灌溉方案可以根据决策变量WS衡量。模型求解得到的优化结果可以反映不同作物在不同阶段和不同情景下的灌溉面积,从而反映出3类研究作物在时段内的用水竞争性以及不同时段间的用水竞争性。因为3个阶段(t
=1,2,3)为3个以规划年为单位的时段,所以在3个时段均需要进行3种研究作物的灌溉。在不同的流量水平,违规概率(p
)和独立违规概率(p
)情况下,作物的优化灌溉面积不同。1)不同流量水平下的灌溉方案分析。
在违规概率(p
)以及独立违规概率(p
)相同时,为避免偶然性,不同流量水平下的作物灌溉面积的变化采用第一时段的1A、2B、3C情景分别分析,模型求解得到研究作物的优化灌溉面积(图3)。可见,对于不同作物,当流量水平增大时,作物地表水灌溉面积增大,同时需要的地下水和外调水进行灌溉的面积就越少,带来的惩罚损失越少,反之亦然。对于3类作物,为满足《民勤县人民政府关于印发民勤县国民经济和社会发展第十四个五年规划和二〇三五年远景目标纲要的通知》中红崖山灌区研究作物种植比例(粮食作物面积:经济作物面积:林业面积为33∶54∶13)约束条件,优化结果显示瓜果类作物的灌溉面积大于粮食作物的灌溉面积,并依次大于蔬菜作物的灌溉面积,此时可以使系统灌溉效益最大。值得注意的是,在第一时段,A或B情景相对于C情景下的独立违规概率较小,导致约束空间变窄,地表水可利用水量变少,所以A和B情景下的各类作物在不同的流量水平下的下限灌溉面积相等。2)不同违规概率和不同独立违规水平下的灌溉方案。

图3 时段1不同研究作物在1A、2B、3C情景地表水灌溉面积的上下限优化结果Fig.3 Optimization results of upper and lower bound of surface water irrigation area for different research crops under scenarios 1A, 2B and 3C in period 1
3个不同时段对应着有动态变换关系的3个作物生长时段,因此不同的违规概率和独立概率水平对应的约束双侧的违规程度会对地表水的优化灌溉面积产生影响。当流量水平以及独立违规概率(p
)相同时,不同违规概率(p
)下作物灌溉面积的变化采取对第二时段1A、2A、3A情景的求解数据进行分析。模型通过求解得到该时段作物的优化灌溉面积(图4)。可见,由于第一时段多余的水量也在这一时段进行灌溉分配,因此这一时段的用水竞争性更大。在LH、MH、HH 3种流量水平情景下,3类作物的优化灌溉面积比第二时段流量水平为L或M时的灌溉面积更大。从情景1A,2A和3A的求解结果可以看出,随着联合违规概率的增大,研究作物的优化灌溉面积在增大,这是因为在相同的流量水平下,决策者可利用的地表水灌溉水量随着联合违规概率的递增而增多。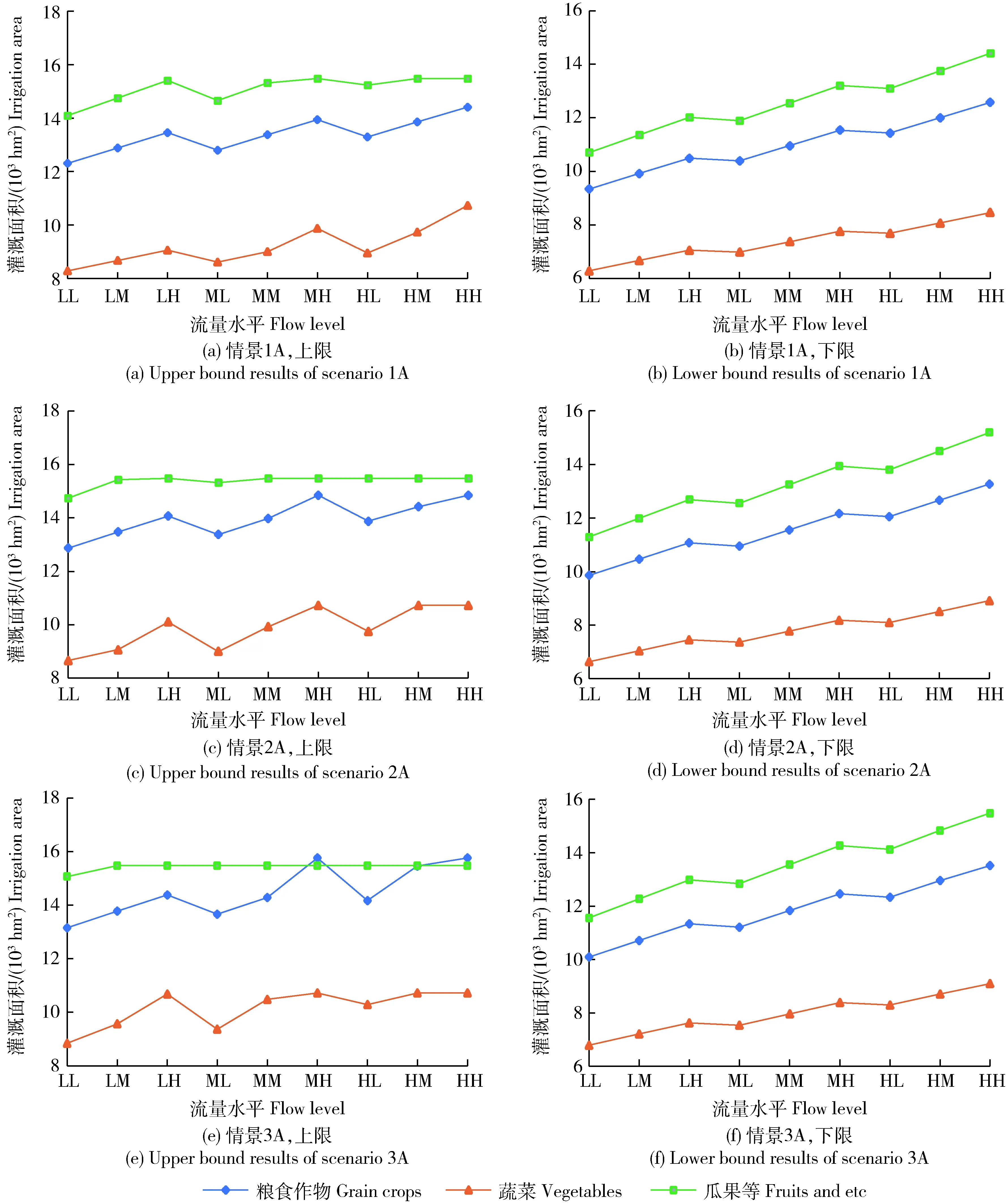
图4 时段2不同研究作物在1A、2A、3A情景地表水灌溉面积的上下限优化结果Fig.4 Optimization results of upper and lower bound of surface water irrigation area for different research crops under scenarios 1A, 2A and 3A in period 2
当流量水平以及联合违规概率(p
)相同,独立违规概率(p
)不同时,分别在2A,2B,2C的情景下进行分析。模型通过求解得到该时段在情景2B和2C的作物优化灌溉面积(图5)。结合图4中情景2A的求解结果,可见在这3种情景下地表水灌溉面积变化趋势不大,而且对于上限结果,瓜果类经济作物变化趋势低于其他两类作物,说明瓜果类经济作物在灌溉时被优先满足。综上,在不同的独立违规概率变化趋势下,瓜果类的灌溉面积大于粮食作物的灌溉面积,蔬菜的灌溉面积最小。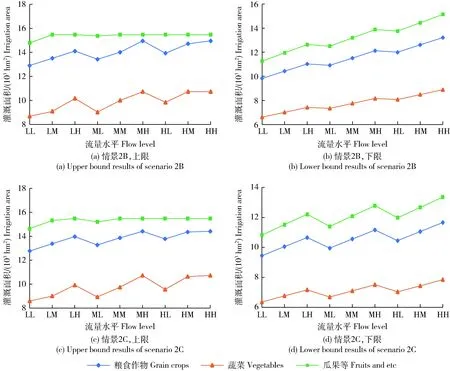
图5 时段2不同研究作物在2B和2C情景地表水灌溉面积的上下限优化结果Fig.5 Optimization results of upper and lower bound of surface water irrigation area for different research crops under scenarios 2B and 3C in period 2
2
.3
.3
灌溉效益在不同的联合违规概率和独立概率变化趋势下,系统获得的灌溉效益也不同。本案例采取的蔡旗断面径流量数据根据桂泽瑛对蔡旗断面径流量的预测研究获得。由于人类活动在2013年以后对蔡旗断面径流量大小产生正向作用,所以本案例获取的径流量上下限区间值差距较大,获得的灌溉效益也会产生相应的结果。图6为模型求解所得到的灌溉效益。可见,灌溉效益随着违规概率的增大而增大,这也符合地表水可利用水量随着违规概率增加而增多,灌溉效益随灌溉面积增大而增大的规律。例如,当分析情景为1A,2A和3A,此时联合违规概率逐渐增大,系统灌溉效益分别为[52.32,107.88]亿元、[56.64,111.62]亿元和[58.87,113.19]亿元。此外,在违规概率相同的情况下,不同的独立违规概率情景下的灌溉效益也不同,并且在3个不同违规概率情况下分别呈现不同的变化趋势。例如,在违规概率p
=0.01时,1A,1B,1C情景下的灌溉效益分别为[52.32,107.88]亿元,[52.57,107.99]亿元和[51.88,107.55]亿元。在B情景下,违规概率为0.01时有最高的灌溉效益。除此之外,B情况下,对于违规概率p
为0.05或0.1时,下限效益值均取得最大值,上限效益值均取得最小值。对于保守的决策者则可以在较高的下限效益值的情景下进行决策,积极的决策者则可以在较高的上限效益值的情景下进行决策。综上,不同的灌溉定额和不同的地表水用于农业灌溉的比例会对作物的灌溉效益产生不同的结果,二者的随机性会直接影响农业系统的经济效益。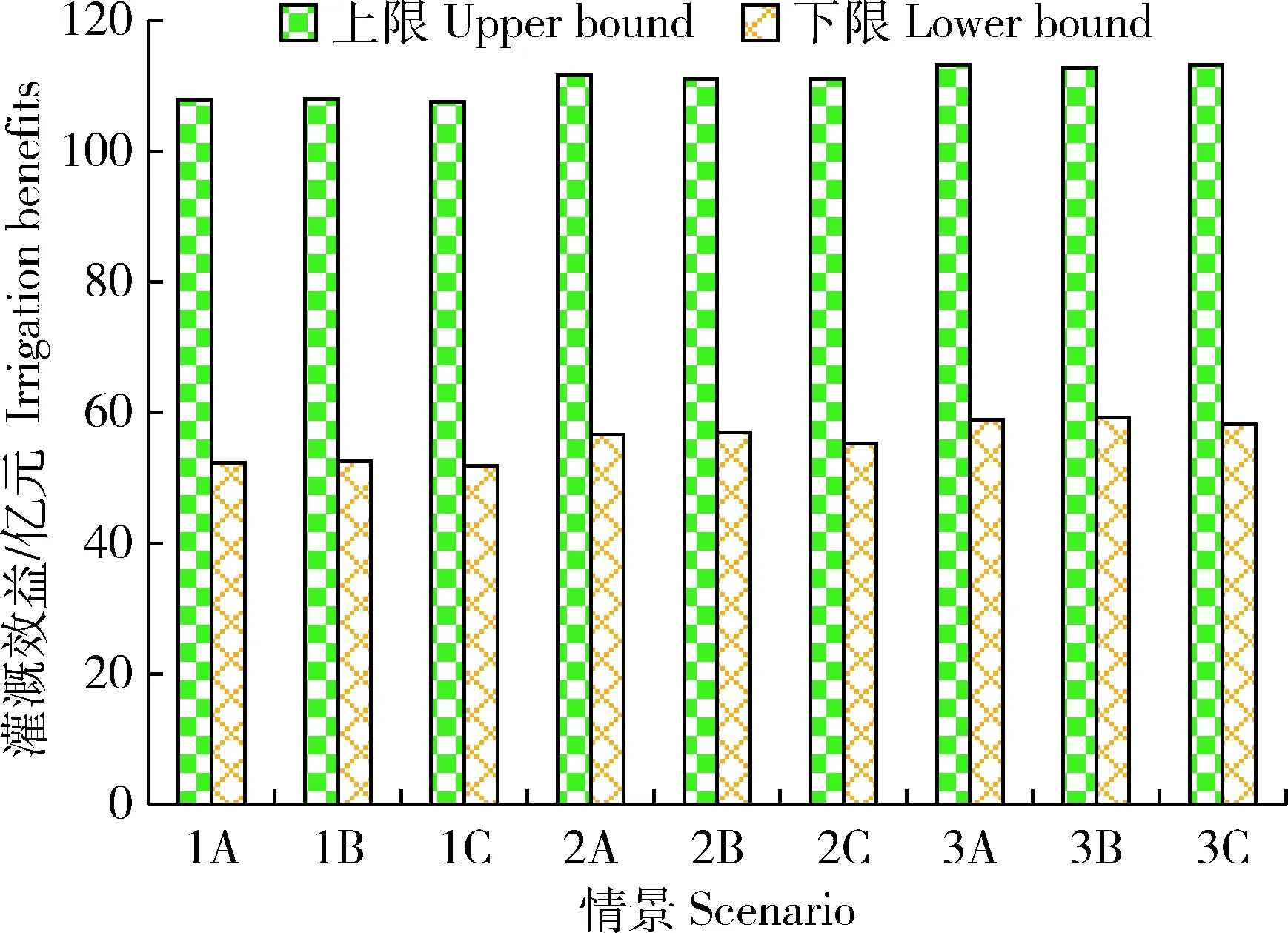
图6 不同情景下的系统灌溉效益Fig.6 Irrigation benefits under different scenarios
3 结 论
本研究结合区间多阶段随机规划、双侧随机机会约束规划和联合概率规划,构建了区间多阶段双侧随机联合概率机会约束规划模型,并将其应用于甘肃省民勤县红崖山灌区,得到了9种情景下的优化灌溉方案。灌溉方案显示,在3个研究时段,粮食作物的用水竞争性小于经济作物的用水竞争性。同时本研究可以衡量在不同的违规风险下系统的灌溉效益和研究作物的灌溉面积之间的权衡关系,系统的灌溉效益随着违规概率的增大而逐渐增大,例如当独立违规概率不变,联合违规概率为0.1时的灌溉效益比联合违规概率为0.01时的灌溉效益上下限值分别增大5.31亿元和6.55亿元;对于研究作物的灌溉面积,灌溉方案显示瓜果类经济作物的灌溉面积最大,粮食作物灌溉面积次之,蔬菜的灌溉面积最小。本研究可以为当地水资源管理者提供不同的决策方案,也可以为类似灌区的农业水资源优化配置提供方法依据。

