一类非参数不确定系统的自适应神经网络重复学习控制①
许昌源 谢树宗 陈强
(浙江工业大学信息工程学院 杭州310023)
0 引言
重复学习控制适用于在无限区间上周期运行的被控对象,利用上一周期运行的数据修正当前周期的控制输入,实现对周期轨迹的零误差跟踪。与其他控制方法相比,滑模控制方法能够实现对被控系统的降阶控制,具有稳定范围宽、动态响应快、鲁棒性强、控制实现简单等优点,能够很好适用于重复学习控制。因而重复学习控制在实际系统中获得了广泛应用,如在机械臂、数控机床、精密加工等领域[1-2]。
经典的重复学习控制通常也被称为重复控制,主要思路是通过在频域内应用内模原理构造周期为T的任意周期信号内模,实现对周期信号的完全跟踪[3-4]。文献[5]针对具有周期性干扰的时滞系统,设计了新型的连续时间重复控制器。文献[6]针对一类线性系统,提出了基于二维连续离散混合模型的不确定系统设计重复控制系统的方法。文献[7]针对一类具有非周期性扰动和时变结构不确定性的严格适当线性系统设计基于观测器的改进重复控制器。
近年来,基于Lyapunov 方法的重复学习控制引起了广泛关注[8-12]。文献[13]针对一类时变参数不确定非线性系统,提出一种周期自适应学习控制方法,并证明闭环系统的全局渐近稳定性。文献[14]针对一类非线性参数化系统提出一种自适应重复学习控制方法,在存在未知常数和周期时间函数的情况下,可以实现自适应系统的全局稳定性和跟踪误差的渐近收敛。然而,实际系统往往存在的负载转矩和未建模动态等非参数不确定性使得参数化的重复学习控制方法不能直接适用。
针对带有非参数不确定性的非线性系统,文献[15]提出了一种新型自适应重复学习控制方法,实现对非参数化不确定的非线性动态系统的周期性轨迹的完全跟踪。文献[16]在重复学习控制中引入Pade 逼近方法解决系统中的不确定问题,并将该方法应用于平面机械手,实现高精度跟踪。文献[17]提出了一种基于backstepping 控制策略的重复学习控制方法来处理具有非参数不确定性的非线性动力系统的周期性跟踪任务,但并未考虑对重复学习律中的学习项进行限幅。文献[18]针对带有非参数不确定性的步进电机,设计鲁棒重复学习控制器,保证转子位置跟踪误差指数收敛到极小的范围内。文献[19]针对工业双轴精密龙门提出一种自适应鲁棒重复控制方法,利用傅立叶级数展开估计和补偿周期性不确定性,进而设计非线性鲁棒项减小轮廓误差。上述文献中,非参数不确定性的界限要求在控制器设计中已知或部分已知,且学习律大多设计为部分限幅学习律,难以保证将学习项限制在指定的界内。
基于以上讨论,本文针对具有非参数化不确定性的永磁同步电机系统,提出一种自适应神经网络重复学习控制方法,实现对周期性期望轨迹的高精度跟踪。针对永磁同步电机中的非参数不确定性,将其分为周期性部分与非周期性部分,其中周期性部分可设计重复学习律进行处理,非周期性部分通过设计神经网络进行估计和补偿,避免使用Lipschitz假设条件。同时,本文设计全限幅学习律对周期性期望控制输入进行估计,与已有的部分限幅学习律相比,该学习律可保证估计值被限制在指定的界内。
1 问题的提出
考虑如下非参数不确定系统

其中,x=[x1,x2,…,xn]T∈Rn为系统状态,u∈R表示控制输入,f(x)和g(x) 为未知光滑有界的非线性函数,其中f(x) 表示系统中的非参数不确定性,g(x) 表示与状态相关的控制增益。
假设1假设存在正常数g0和g1,满足g(x)≥g0>0,且≤g1。
本文考虑周期为T的有界期望轨迹xr=[x1r,x2r,…,xnr]T,即xr(t)=xr(t -T),可构造期望控制输入

满足

由xr的周期性可知,ur同样为周期为T的周期信号,即ur(t)=ur(t -T)。
本文控制目标为,根据期望轨迹xr和期望控制输入ur的周期特性,设计神经网络重复学习控制器u,实现系统状态x对期望轨迹xr的高精度跟踪。
2 神经网络重复学习控制
2.1 误差定义与滑模面设计
定义跟踪误差为

设计滑模面为

其中ci(2 ≤i≤n) 为设计参数,并使得多项式en +cnen-1+…+c2e1为Hurwitz 多项式。
对式(5)求导可得:
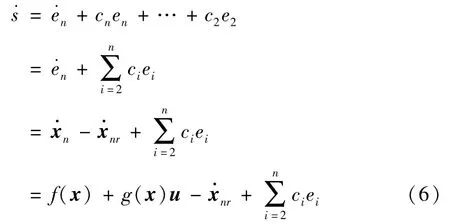
由式(6)可得:
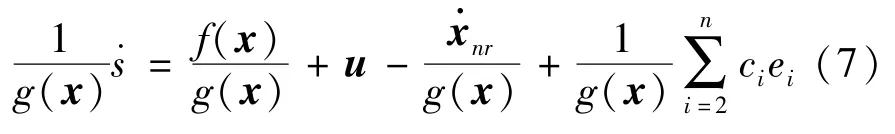
在滑模动态式(7)中,系统不确定性并无表现出明显的周期特性,因而难以直接基于式(7)设计重复学习控制器。为此,本文构造周期性期望控制输入式(2),并由式(7)可得:
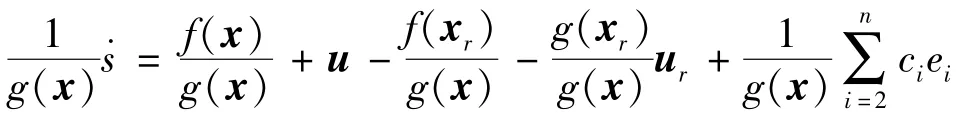
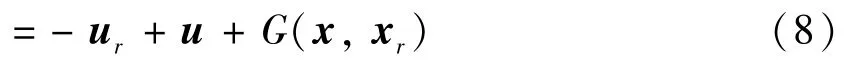
其中,非周期不确定性G(x,xr) 表达式为
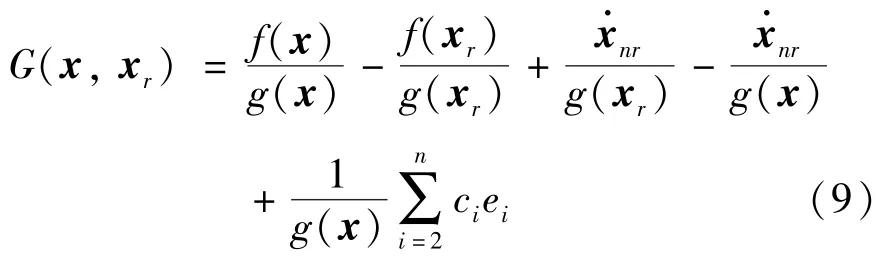
非周期不确定项G(x,xr) 可通过神经网络进行估计,由式(2)以及f(xr)、g(xr) 的有界性可知,期望控制输入ur为有界函数,即存在正常数满足| ur|≤。根据期望控制输入ur的周期性,可设计重复学习律为
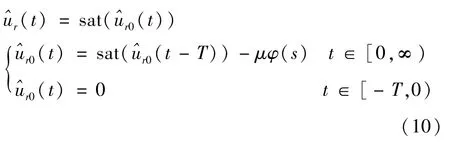
其中,μ为学习增益,sat(·)为饱和函数,对任一标量a有

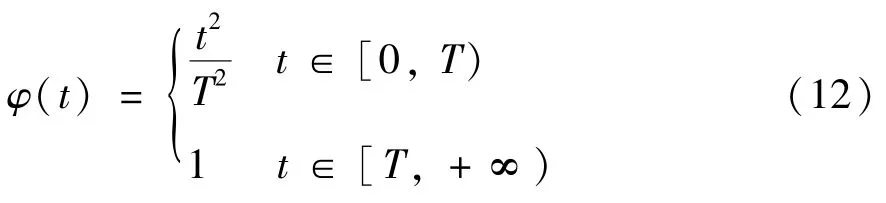
本文通过构造周期参考输入信号ur设计重复学习律进行估计,而非周期不确定性G(x,xr) 通过神经网络进行估计补偿,以实现对给定周期信号的高精度跟踪。
注1为处理非周期不确定项G(x,xr),现有文献[18]多采用局部Liptchiz 条件将其放缩为参数不确定进行处理。与文献[18]不同,本文采用神经网络估计该非周期不确定项,从而避免使用Lipschitz 假设条件。
注2为保证估计值的有界性,现有文献[15,18]中多采用部分限幅形式的学习律,形式为-φ(t)μs。然而,未限幅项φ(t)μs的存在,使得难以被限制在指定界内。与文献[15,18]不同,本文设计的全限幅学习律式(10)由于对和分别进行限幅,因此能够确保被有效限制在指定的界内。
2.2 神经网络重复学习设计
设计神经网络逼近不确定函数为
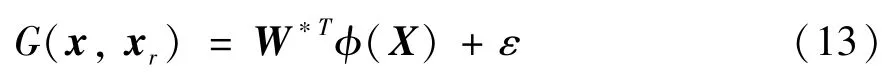
其中,X∈ΩZ为输入向量;ΩZ∈R为一紧凑子集;ε为近似误差,存在一个正常数εN,满足| ε|≤εN;ϕ(X) ∈Rν为神经网络的基函数;ν(ν >1) 为神经网络的节点数;W*∈Rν为理想权重矩阵,定义为
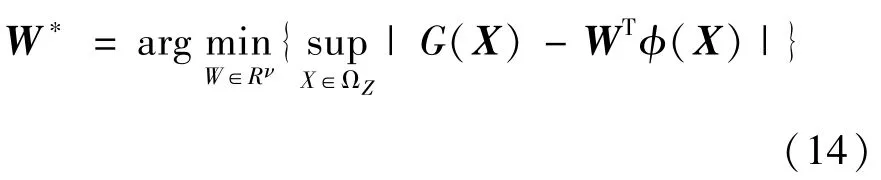
其中,W∈Rν为权重矩阵,选择以下sigmoid 函数

其中,l1、l2、l3、l4为适当的正常数。
选取Lyapunov 函数
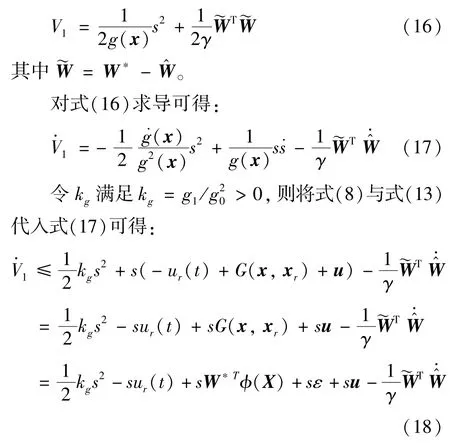
由式(18)可设计控制器为
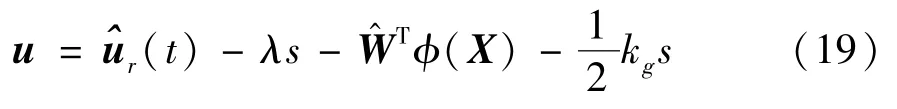
其中,λ、kg >0,将式(19)代入式(18)可得:

其中,σ >0,将式(21)代入式(20)得:
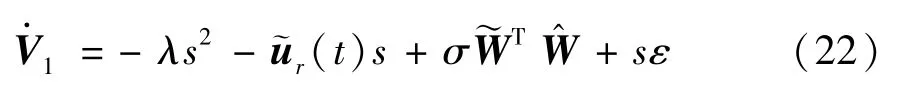
3 收敛性分析
引理1[20]对于给定标量a和b,若| a |≤ˉb,其中ˉb为b的上界,以下不等式成立

定理1针对系统式(1),给定周期性期望轨迹xr,设计重复学习控制器式(19),重复学习律式(10),自适应律式(21),系统的跟踪误差可收敛至原点附近的邻域内。
证明选取Lyapunov 函数

对式(24)求导,并根据性质a2-b2=(a+b)(a -b) 可得:
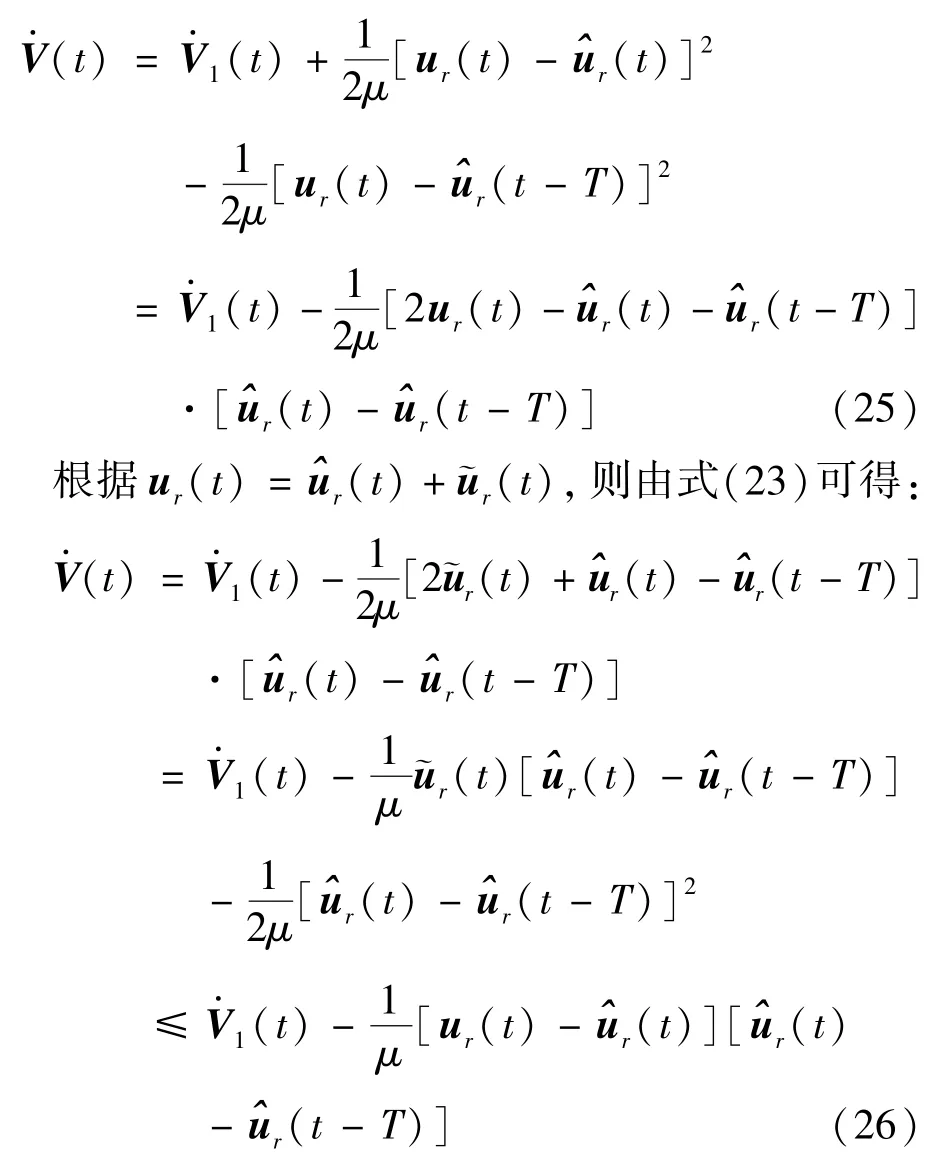
根据式(10),则由式(26)可得:
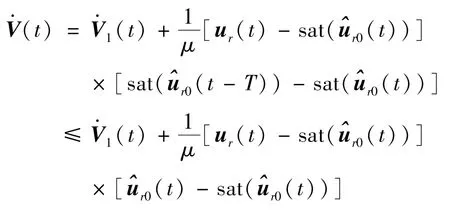

将式(10)代入式(27)并根据引理1 可得:
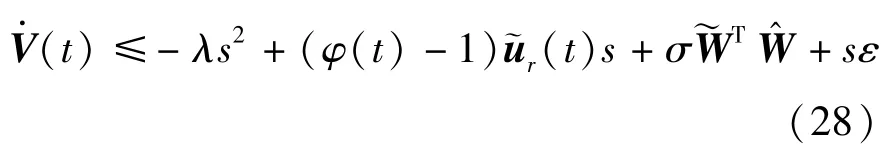
根据杨氏不等式可得:
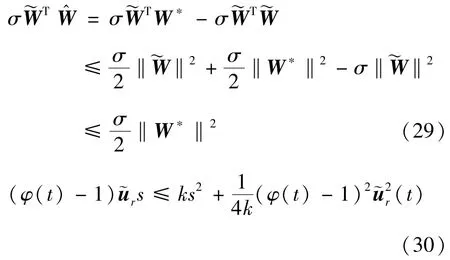
将式(29)和(30)代入式(28)可得:

根据滑模面式(5)的定义,跟踪误差e1能够渐近收敛到零点附近的邻域内。
4 仿真结果及分析
本节通过永磁同步电机模型进行验证所提神经网络重复学习方法的有效性,并将本文所提方法(M1)与自适应神经网络控制方法(M2)进行对比。
永磁同步电机模型表达式如式(35)所示。

其中,iq为q轴定子电流,J是惯性系数,B为粘滞摩擦系数,np是极对数,ϕf是磁链,TL(θ) 表示与位置有关的负载转矩,θ、ω分别是转子位置和角速度。


表1 永磁同步电机的模型参数
仿真中设置转子位置的参考轨迹x1r(t)=0.2πsin(2πt),其周期为T=1 s,永磁同步电机的初始状态设置为x1(0)=0,x2(0)=0。本文方法(M1)的控制律如式(14)所示,神经网络参数为l1=3.9,l2=10,l3=8,l4=0.5;控制参数设置为kg=0.02,λ=0.02,[0,0,0,0]T;参数σ=5,μ=0.5,γ=0.9。
自适应神经网络控制方法[21](M2)的控制律为
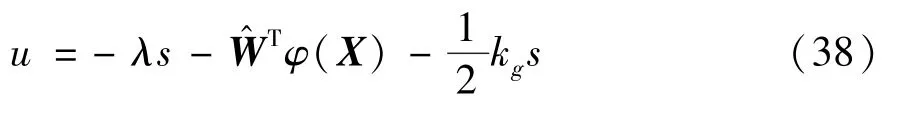
神经网络参数为l1=15,l2=2,l3=10,l4=0.5,控制参数的设置与M1 方法一致,即kg=0.02,λ=0.02,[0,0,0,0]T,参数σ=5,γ=0.9。
仿真结果如图1~图5 所示,图1 为M1 和M2方法的位置跟踪效果图,可以看出本文所提M1 方法较M2 具有更好的跟踪精度。图2 和图3 分别为位置跟踪误差对比图和速度跟踪误差对比图,通过对比可以看出M2 方法的跟踪误差仍具有一定的周期性。与M2 相比,本文提出的M1 方法由于能够有效补偿周期不确定性,因而可以减小稳态跟踪误差,实现对给定周期性期望轨迹的精确跟踪。图4 给出了M1 方法的重复学习律对期望控制输入ur的估计图,从图中可看出式(12)中φ(t) 的设计,使得参考输入的估计值保持连续性,且重复学习律式(10)对于周期性非参数不确定性实现了较好的补偿性能。两种方法的控制输入如图5 所示,从图中可以看出,两种方法的控制信号幅值比较接近。仿真结果显示了本文所提出的重复学习方法能较好地处理系统中的非参数不确定性,实现了对给定周期期望轨迹的精确跟踪。
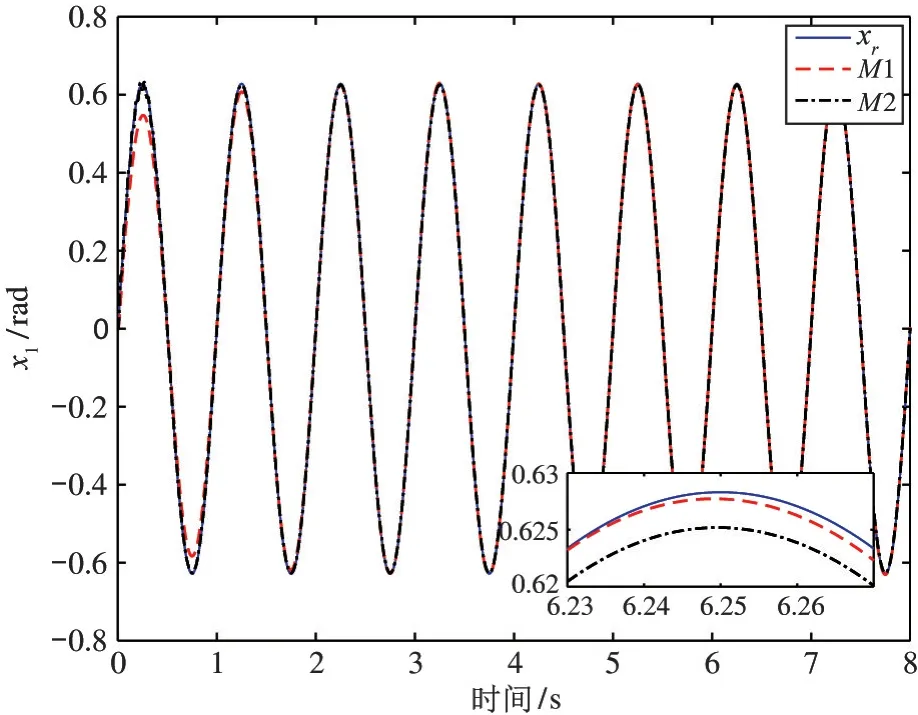
图1 位置跟踪效果
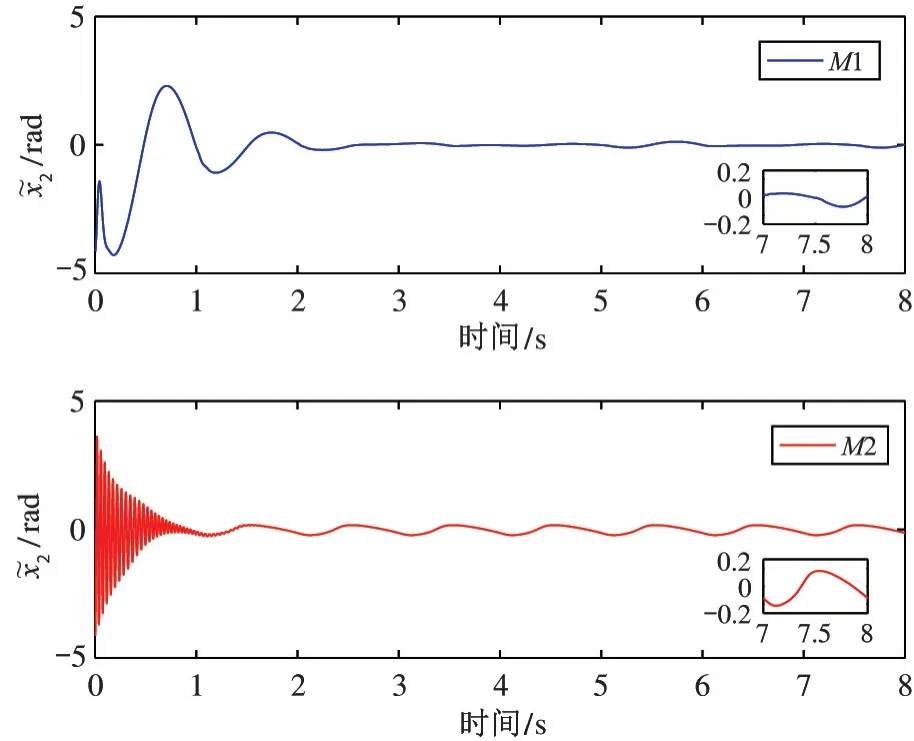
图2 位置跟踪误差
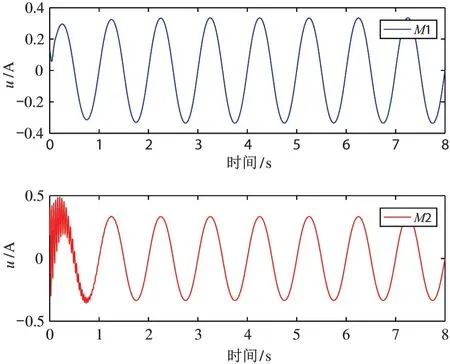
图3 速度跟踪误差

图4 M1 方法期望控制输入ur 的估计
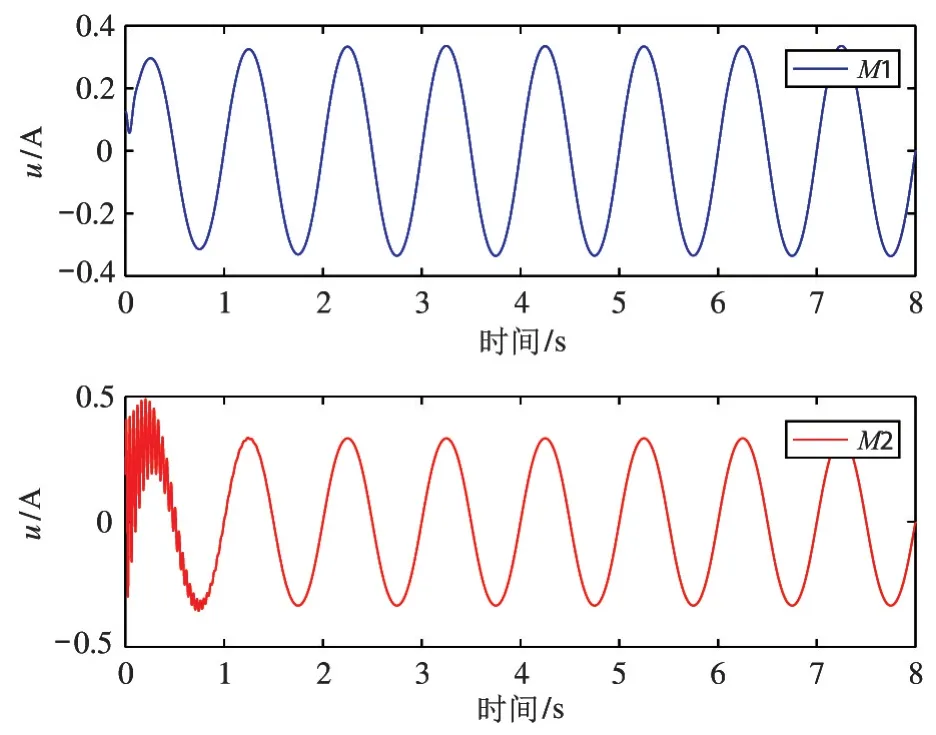
图5 控制输入
5 结论
本文针对一类非参数不确定系统提出一种自适应神经网络重复学习控制方法。利用期望周期轨迹的周期特性构造周期控制输入信号,并设计全限幅学习律进行估计,保证学习项的有界性。基于Lyapunov 方法设计重复学习控制器,并设计神经网络对非周期不确定性及干扰进行估计,使跟踪误差收敛于零点附近的邻域内,实现高精度跟踪。最后,基于Lyapunov 方法对误差收敛性进行了分析,并通过仿真以及电机实验验证了本文所提方法的有效性。

