构配件性能缺陷对模板支撑体系承载性能的影响

陆征然，林志浩，张 磊，郭 超

(1.沈阳建筑大学土木工程学院，辽宁 沈阳 110168;2.沈阳建筑大学管理学院，辽宁 沈阳 110168;3.中国建筑股份有限公司技术中心，北京 100037)

扣件式钢管模板支撑体系由于具备搭设方便、承载力高、适用范围广等优点，成为工程建设中使用最为广泛的一种形式。然而，作为一种临时性结构，其安全性没有得到足够的重视，导致坍塌事故时有发生[1]。

近些年来，国内外学者对模板支撑体系承载性能展开了较多研究。L.Jia等[2]考虑直角扣件螺栓拧紧力矩、部件状况(新或旧)等因素，讨论直角扣件的力学性能对支架承载性能的影响。陆征然等[3]利用Matlab软件编写程序分析了不同搭设参数条件下，管径、壁厚、转动刚度、弹性模量等构造因素对承载力的影响。索小永等[4]通过对完好与漏设水平剪刀撑空间模型的非线性屈曲分析，探究二者极限承载力及失稳形态，强调了水平剪刀撑构造作用的重要性。此外，还有学者针对模板支撑体系的各种缺陷、边界条件展开了大量有限元模拟及可靠度分析[5-6]。

模板支撑体系在周转使用的过程中，扣件和钢管必将产生一定的磨损、锈蚀，这将导致各构配件材料性能、截面几何属性、扣件约束功能退化，此处将上述统称为构配件的性能缺陷。针对这一实际问题，学者也展开了相应研究[7-8]。

目前，对于模板支撑体系的研究多针对于构造因素及初始缺陷等[9-11]，而构配件性能缺陷对模板支撑体系承载性能的影响研究相对较少。基于此，笔者以搭设步距为1.5 m，纵横向间距均为1.2 m的模板支撑体系为对象，在ABAQUS中建立有限元模型，利用Python编制脚本程序，研究具有不同缺陷程度的构配件，在空间位置随机分布条件下，支撑体系稳定承载力的变化；对于构配件的性能缺陷(即构配件性能退化)，通过在原有构配件性能参数上按照不同百分比折减的方式进行考察；在构配件的空间分布上，按照具有性能缺陷的构配件是否出现在同一根立杆上，研究前述各性能缺陷耦合程度的差异对支撑体系承载性能的影响规律。研究表明:存在性能缺陷的构配件分布位置(从立杆排数上看)以满排且集中的状态出现，架体稳定承载力达到最低;不同构配件性能缺陷及抽样比例下支撑体系失稳模式会发生变化。

1 影响因素及参数选取

经查阅文献[5]以及施工现场实际调查，发现管径、壁厚的减小、弹性模量的变化、扣件转动刚度的降低，属于普遍现象。因此，笔者分别选取管径D、壁厚t、弹性模量E以及扣件转动刚度SPR作为构配件在材料性能、几何属性、约束功能方面的代表性参数。参考文献[12]中对钢管尺寸及材料性能的现场测量结果，经统计分析得出D、t、E均服从正态分布，具体参数如表1所示。

表1 钢管尺寸及性能参数Table 1 The steel pipe size and performance parameters

此外，《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)[13]将钢管截面管径×壁厚由48 mm×3.5 mm修改为48.3 mm×3.6 mm。因此，按照新规范的要求，以48.3 mm×3.6 mm作为几何属性完好状态下的钢管截面尺寸，2.06×105MPa作为材料性能完好状态下的弹性模量。同时，《建筑施工临时支撑结构技术规范》(JGJ 130—2013)[14]中规定直角扣件的转动刚度为35(kN·m)/rad，文献[15]通过对施工现场扣件拧紧力矩进行实际测量得出相应转动刚度服从截尾正态分布，其均值为27.16(kN·m)/rad，变异系数0.333，截尾为下限8.94(kN·m)/rad。可以看出，实际工程中扣件刚度很难达到规范的规定值。此外，文献[16]中指出新的扣件和钢管表面涂有油漆，同时二者接触面之间还可能存在突出油漆颗粒造成的间隙，由此导致的咬合力降低使得很多新扣件的刚度比周转多次后的刚度还要低。考虑扣件刚度的随机性大以及下限值较低，文中偏于安全的将性能完好条件下的扣件转动刚度取为25(kN·m)/rad。

按照表1中影响因素分布的均值及90%置信区间，并结合影响因素性能完好状态下的取值(将此状态性能指标视为100%)，分别确定D、t、E参数3个等级下的取值。对于扣件转动刚度，由于其离散性较大，根据文献[15]中的数据分布，在合理范围内人为地设置其在90%性能指标的基础上以20%的比例逐级降低，并添加其完好状态下的取值在后续分析中提供参照对比，共形成5个等级下的取值。按照上述方式所形成各影响因素具体取值如表2所示。

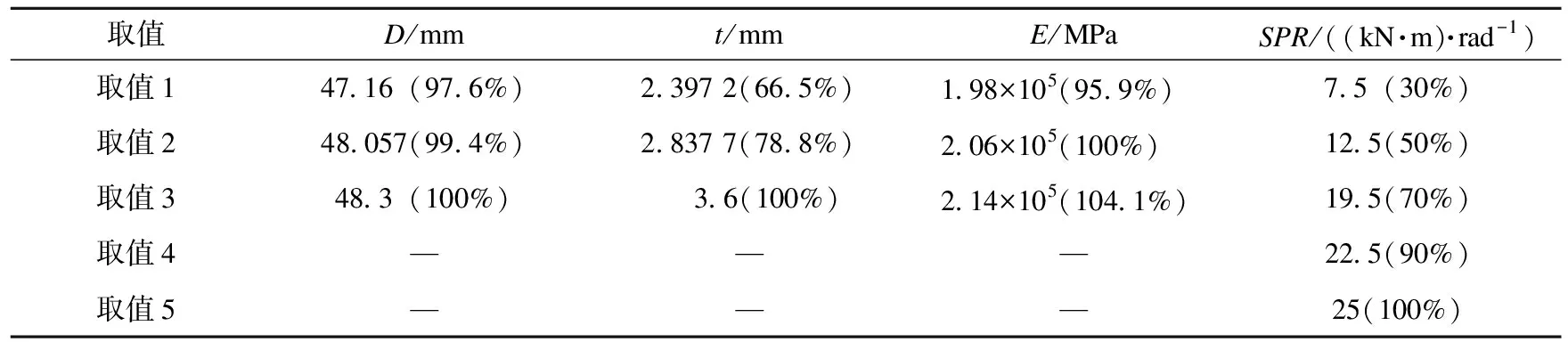
表2 影响因素取值及性能指标Table 2 The influencing factors and performance indicators

2 随机有限元的抽样规则制定

为了有效模拟具有不同程度性能缺陷的构配件，在施工现场支撑体系实际搭设中空间位置的随机性，利用Python编制脚本程序，驱动ABAQUS有限元软件，进行考虑具有缺陷的立杆占比、构配件性能缺陷因素耦合数量及程度、构配件性能指标等条件下的随机有限元分析，各影响因素耦合方式如表3所示。

表3 影响因素耦合方式Table 3 The coupling mode of influencing factors

其中，对于多因素耦合中深/浅层次两种耦合形式，以D+E+SPR为例绘制模板支撑体系随机有限元分析流程图如图1所示。

图1 多因素深/浅层次耦合支撑体系随机有限元分析流程Fig.1 The stochastic finite element analysis flow of multi factor deep / shallow coupling support system

对表2、表3中的等级参数进行交叉组合，共形成222种计算工况。基于蒙特卡罗法的基本原理，计算在相应工况下的体系稳定承载力，并且每种工况循环计算1 000次。

3 模板支撑体系承载性能的随机有限元分析

3.1 搭设参数的取值

《建筑施工模板安全技术规范》(JGJ 162—2018)[17]规定模板支架扫地杆高度为0.2 m。《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)[13]规定立杆伸出顶层水平杆中心线至支撑点长度不应超过0.5 m。文献[18]研究扫地杆高度发现，当其为0.2 m时支撑体系承载力最高;当其大于0.4 m时承载力下降加快。考虑扫地杆高度过低不便于设置，建议扫地杆高度应小于0.4 m。综上，笔者选取的支撑体系计算模型搭设参数如下:立杆步距1.5 m，纵、横向间距均为1.2 m，扫地杆高度与立杆顶部伸出考虑其边界值分别取0.4 m和0.5 m。

3.2 有限元计算结果分析

3.2.1 单因素对体系稳定承载力的影响

分别对D、t、E、SPR四种因素，在不同性能指标条件下模板支撑体系稳定承载力的随机有限元计算结果进行统计，发现均服从正态分布，其统计结果如表4所示。

从表4中可以看出，D、t、E三种因素单独作用，对于稳定承载力的影响并不明显。其中，当抽取的立杆占比为80%，且其壁厚指标为66.5%时，稳定承载力下降最多，但仅3.6%;其余工况下，体系稳定承载力的下降程度均在2%以内。扣件转动刚度SPR对体系稳定承载力的影响最大，对其进行详细分析。

表4 单因素影响下体系稳定承载力计算结果分布统计Table 4 The statistics calculation results of system stable bearing capacity under the influence of single factor

(1)SPR性能指标退化的影响:当SPR性能指标为90%时，不同立杆占比下的体系稳定承载力下降幅度较小，均在6.2%以内;随着SPR性能指标的不断降低，相同立杆占比下的稳定承载力降低幅度逐渐增加。当SPR性能指标为30%时，承载力下降幅度最大，其中当抽取的立杆占比为80%时，稳定承载力下降了51.8%。当SPR性能指标为30%，抽取的立杆占比为40%和60%时，其稳定承载力分布的标准差相近，且大于立杆占比达到80%时承载力分布的标准差。

综上可以说明：前两种抽样比例下，具有缺陷的扣件空间位置分布对体系稳定承载力影响较小，且该规律同样适用于其他三种扣件性能指标。

(2)具有缺陷的扣件空间分布影响:通过对不同扣件性能指标工况下最低/高稳定承载力缺陷扣件的空间分布进行分析，发现具有较强的共性规律。现以抽样立杆占比80%，SPR30%为例并进行说明，分别绘制该条件下体系稳定承载力最低/高时，缺陷扣件的位置分布(见图2),其对应的支撑体系失稳模式如图3所示。

图2 缺陷扣件位置分布Fig.2 The location distribution of defective fasteners

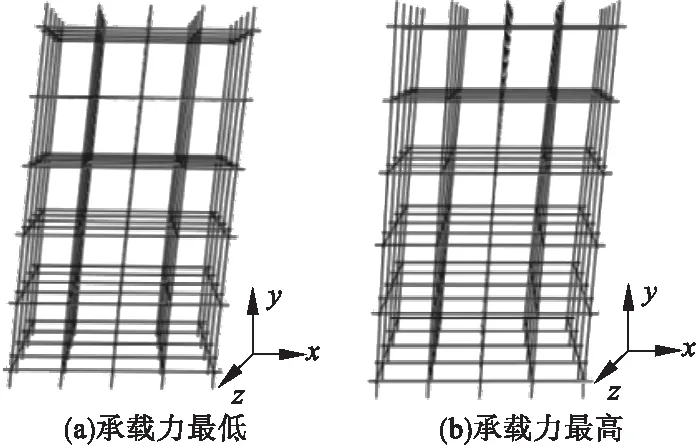
图3 支撑体系失稳模式Fig.3 The instability mode of support system

对比图2和图3可以看出，存在性能缺陷的扣件分布位置越集中(从立杆排数上看，缺陷扣件满排且相邻)，其整体承载力越低。支撑体系失稳模式较性能完好状态下的失稳模式发生了变化，由最开始的沿z轴正方向失稳逐渐转变到沿x轴正方向失稳。在全部扣件完好条件下，模板支撑体系的各杆件发生同一方向的整体失稳且单杆稳定承载力最高；当具有性能缺陷的扣件按照图2(b)分散布置时，各杆件稳定性最弱的方向不一致，当其沿各自稳定性最弱的方向发生失稳时，由于扣件的连接，相互制约，导致其稳定承载力较高；当具有性能缺陷的扣件按照图2(a)聚集布置时，导致多数杆件稳定性弱的方向再次重合，各杆件发生同一方向的整体失稳且单杆稳的概率增加定承载力最低。

因此，结合图2、图3，建议对于存在性能缺陷的扣件应尽量分散、不满排地布置于多列(排)相邻立杆上。

3.2.2 多因素功能退化耦合作用对体系稳定承载力的影响

对多因素、不同耦合形式模板支撑体系稳定承载力的随机有限元计算结果进行统计，发现均服从正态分布。部分多因素耦合条件下的体系稳定承载力均值如表5所示，其对应标准差如表6所示。

表5 部分多因素功能退化深/浅层次耦合稳定承载力均值Table 5 The mean value of deep/shallow coupling stable bearing capacity with partial multi factor functional degradation N

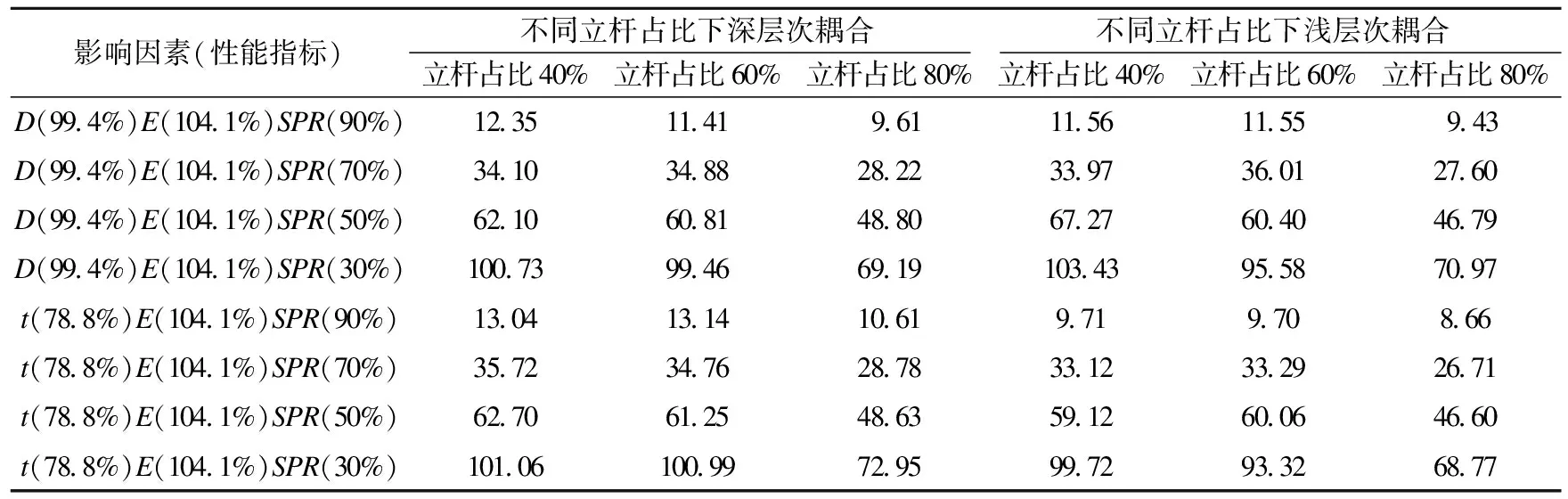
表6 部分多因素功能退化深/浅耦合稳定承载力标准差Table 6 The standard deviation of deep / shallow coupling stable bearing capacity with partial multi factor functional degradation N

从表5可看出，t、E、SPR三种因素耦合作用对体系稳定承载力的影响比D、E、SPR耦合时略高。对比表5和表4，发现多因素耦合时，对稳定承载力产生影响的最主要因素，为SPR。

将多因素在深、浅层次耦合条件下的稳定承载力计算结果进行比较后发现，只有D(99.4%)、E(104.1%)、SPR(30%～90%)四种情况下深层次耦合的稳定承载力低于浅层次耦合。由此说明大多数情况下，多种影响因素性能指标降低同时作用于一根立杆及立杆上的全部扣件时，对体系稳定承载力的影响更大。

同时，当D、E、t性能指标一定时，随着SPR指标的提高，深、浅层次耦合体系稳定承载力的差距逐渐减小，当SPR性能达到90%时，二者稳定承载力几乎相同，说明当D、E、t保持足够的性能指标时，随着扣件SPR性能的提升，缺陷杆件位置分布对体系稳定承载力的影响逐渐减小。

从表6可以看出，t、E、SPR三因素浅层次耦合的体系稳定承载力分布标准差小于深层次耦合，并且随着SPR性能指标的提高，二者差距逐渐减小。说明当t、E、SPR的性能指标一定时，多因素深层次耦合对体系稳定承载力的影响高于浅层次耦合，但随着SPR性能指标的提高，二者对体系稳定承载力的影响逐渐相近。D、E、SPR三因素浅层次耦合下的承载力分布标准差绝大部分小于深层次耦合，但二者相差较小。说明大多数情况下，当D、E、SPR的性能指标一定时，两种耦合形式对体系稳定承载力的影响相近，并且随着SPR性能指标的提高影响程度逐渐降低。同时，浅层次耦合下D、E、SPR承载力分布标准差普遍高于t、E、SPR，说明当E、SPR的性能指标一定时，浅层次耦合形式下t性能指标变化对体系稳定承载力的影响要高于D。

此外，在构配件性能指标一定的条件下，抽取立杆占比为40%、60%时，稳定承载力分布的标准差相近，且大于抽样立杆占比80%时的标准差，可以说明，前两种构配件性能指标下，具有缺陷的构配件占比及空间位置分布对体系稳定承载力的影响较大。并且，通过对其余工况下的体系稳定承载力数据进行比较分析，发现该规律同样适用。

对各工况下最低/高稳定承载力缺陷构配件的空间分布状况进行分析，发现存在较强的共性规律。以t(66.5%)、E(95.9%)、SPR(30%)为例，分别绘制该条件下深/浅层次耦合、抽取不同比例立杆，体系稳定承载力最低/高时缺陷的构配件位置分布，如图4所示。抽样立杆占比80%时对应的体系失稳模式如图5所示。

图4 不同耦合程度及立杆占比下稳定承载力最高/低时的缺陷构配件分布Fig.4 The distribution of defective components and fittings under different coupling degree and proportion of vertical pole when the stable bearing capacity is the highest / lowest

图5 深/浅层次耦合支撑体系失稳模式Fig.5 The instability mode of deep / shallow coupled support system

从图4可以看出，深层次耦合形式下，存在性能缺陷的构配件分布位置越集中(从立杆排数上看，缺陷构配件满排且相邻)，其整体承载力越低，且这种分布规律随着具有缺陷杆件总体占比的提升更加明显。

浅层次耦合形式下，体系稳定承载力变化主要由具有性能缺陷的扣件分布位置决定:存在性能缺陷的扣件，在体系内部占比越高且布置越集中(从立杆排数上看，缺陷扣件所在的立杆满排且相邻)，其整体承载力越低。并且，这种分布规律随着具有缺陷杆件总体占比的提升更加明显。此外，从图4(b)、(d)中可看出，当D、E、SPR性能指标变化的情况同时出现在一根立杆，且该类杆件不成排、相邻地布置(即间隔距离越大)，架体承载力越高。

结合表5与图5对于存在缺陷的构配件应搭配、间隔使用，尽量不要将具有缺陷的构配件满排、紧邻地布置。

4 结 论

(1)单因素分析中，D、t、E三种因素性能退化对于体系稳定承载力的影响并不明显，SPR性能退化对体系稳定承载力的影响最大。其中，当SPR性能指标仅为30%，抽取立杆占比为80%时，稳定承载力下降最多，为51.8%。此外，在SPR性能指标30%的条件下，抽取的立杆占比为40%和60%时，具有缺陷的扣件空间位置分布对稳定承载力影响较大。但当立杆占比达到80%时，具有缺陷的扣件空间位置分布对稳定承载力影响较小。

(2)多因素耦合对承载力影响以SPR为主导。其影响程度随着SPR性能指标的提高而逐渐降低。

(3)杆件自身稳定性最弱的方向并不一致，具有性能缺陷扣件的分布位置会直接影响整体的失稳方式，从而对架体的稳定承载力产生影响。结合计算结果、相应失稳模式、缺陷构配件分布位置，考虑实际使用过程中的安全性，支撑体系搭设过程中存在缺陷的构配件应搭配、分散间隔使用，尽量避免将具有缺陷的构配件满排、紧邻地布置。