计及电压预测的主动配电网分布式电源在线优化决策方法

席向东，侯香臣，萨仁高娃，朱星旭，孙哲彬，梁涛，刘鹏宣，王晓櫆，李翠萍，李军徽

(1. 内蒙古电力经济技术研究院，呼和浩特市 010010；2. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林省吉林市 132012)

0 引 言

在“双碳”背景下，配电网中分布式电源的接入量越来越大[1]。伴随着配电网分布式电源的渗透率逐渐增大，配电网逐渐从无源变成了有源，与此同时也使得配电网具有了一定的主动性，于是便出现了主动配电网的概念[2-6]。主动配电网具有主动管理分布式电源、储能设备的功能，其可以通过主动调控分布式电源以及储能设备的输出设定值使配电网的运行经济型最优[7-8]。

针对主动配电网主动调控的问题，相关学者在传统电力系统在线优化潮流研究的基础上对该问题进行了展开研究。文献[9]提出了一种分布式最优潮流优化算法，其主要是利用交替方向乘子法(alternating direction method of multipliers，ADMM)解决了集中式优化所面临的计算信息量过大的难题。文献[10]提出了一种改进的粒子群算法，其主要是在建立双层联合优化调度模型的基础上，利用所提改进算法进行优化调度模型的求解。文献[11]提出了一种割平面一致性算法，该算法主要是在对潮流方程线性近似的基础上，利用拉格朗日对偶松弛技术对集中式模型进行解耦分析，进而求解各个解耦区域的最优解。文献[12]提出了一种基于数据自适应鲁棒优化的经济调度方法。

上述文献对主动配电网主动调控问题的研究都是针对5 min及以上时间段的。由于分布式能源的出力具有极强的波动性，这就会导致在5 min及以上时间段所制定的分布式能源输出设定值是不经济的甚至是无效的。针对这个问题相关学者提出了时变最优潮流算法并对该算法进行了相关的展开研究。文献[13]提出了一种双馈电机机群并网系统时变最优潮流的优化追踪算法。文献[14]提出了一种配电网分布式时变最优潮流在线优化算法，其主要是将配电网划分成若干子区域，然后将各区域之间的灵敏度进行解耦，进而使各区域在仅获取内部信息以及边界信息的条件下进行数据交换，从而完成时变最优潮流问题的求解。文献[15]提出了一种分布式反馈控制算法，其主要是持续驱动逆变器输出功率以解决交流最优潮流问题。文献[16]提出了一种考虑对偶投影梯度法的在线优化算法，该算法可以在不明确了解系统模型的情况下将最优潮流的解引导至最优解，并且可以实时跟踪最优解。文献[17]提出了一种时变激励的配电网在线优化算法，其可以在时变过程中时刻满足运行约束的条件下，使得配电网的整体运行效益最大。文献[18]提出了仅需要本地量测信息即可实现在线优化的方法，但其无法考虑电压上下限约束的问题。文献[19]提出了一种在连续动作域中使用基于拉格朗日的深度强化学习的实时最优潮流方法。文献[20]提出了分布式在线优化算法，其主要是将配电网各区域之间进行解耦，然后在各区域边界条件以及内部信息已知的条件下进行信息交互，从而求解时变最优潮流问题。文献[21]提出了一种参数分布最优潮流方法，该方法将最优调度策略和潮流状态作为可再生能源输出的解析函数。文献[22]提出了一种分布式实时最优潮流控制策略，借助双向通信和分布式传感器等最新的通信技术，所提方法可以避免负荷预测的需要。文献[23]提出了一种交流最优潮流实时算法，该算法使用二阶信息在快速时间尺度上提供次优解，并且可以显示当估计的二阶信息足够准确时的最优潮流解。文献[24]提出了一种基于深度神经网络和Levenberg-Marquardt反向传播的双延迟深度确定性策略梯度方法，该方法可以提高交流最优潮流的计算性能。文献[25]提出了一种基于动态最优潮流(dynamic optimal power flow，DOPF)的调度优化算法，该算法主要是用以减轻可再生能源发电的预测限制。

文献[13-25]对主动配电网秒级的时变最优潮流算法展开了相关研究，但是其未考虑分布式电源当前时段的决策值对未来时段决策值的影响，即储能设备在当前时刻依据所决策的充放电功率所进行的能量变化，会影响未来时段内储能设备的决策值。因此针对该问题，本文提出一种计及电压预测的主动配电网分布式电源在线优化决策方法，就已有算法存在的未考虑当前时段决策值对未来时段决策值的影响进行改善。从而实现在考虑分布式电源当前时段决策值对未来时段决策值影响的条件下，系统运行经济性最优的目标。首先，基于配电网开环运行的特性进行网络电压灵敏度的求取。之后利用负荷波动值并结合所求电压灵敏度进行配电网潮流状态的预测。进一步利用网络潮流状态的预测值进行分布式电源的决策。然后依次迭代从而实现对配电网时变最优潮流的求解。

本文的主要创新性总结如下：

1)针对含大量分布式光伏电源以及储能电源的配电网提出一种时变最优潮流在线优化决策方法，该算法能够在保证各时刻各节点电压均在合理范围内的前提下，进行时变最优潮流的追踪求解。

2)针对未来时段配电网节点电压状态，基于电压灵敏度思想进行预测求解，然后用预测值进行分布式能源的决策，避免负荷波动进行潮流计算后再用计算结果进行决策的过程。

3)与现有在线优化算法相比，本文所提在线优化决策方法不仅考虑当前时间段对储能能量的需求，而且还可以根据未来时刻对储能能量的需求制定当前时间段储能电源的充放电计划。

1 问题的数学描述

本文研究的是含分布式光伏以及储能的配电网时变最优潮流追踪问题，其核心是如何在各节点注入有功功率不断变化的过程中，在满足相应约束的条件下，决策可以使配电网运行目标趋于最佳的分布式电源决策设定值。

基于本文所研究的问题，构建含分布式光储配电网的时变最优潮流的模型。

1.1 目标函数

(1)

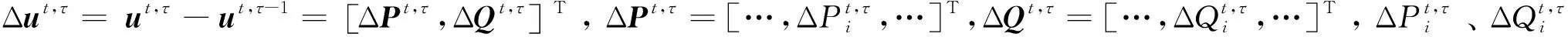
针对不同的电源，Ct,τ(Δut,τ)表示的含义相同，均表示电源的运行成本相较于上一时刻的变化量，若为光伏电源时，则可以表示为：Ct,τ(Δut,τ)=apv(ΔPt,τ)2+bpv(ΔQt,τ)2；若为储能电源时，则可以表示为：Ct,τ(Δut,τ)=ab(ΔPt,τ)2+bb(ΔQt,τ)2。apv、bpv分别为光伏电源的有功、无功调节成本系数；ab、bb分别为储能的有功、无功调节成本系数。

1.2 约束条件

1)潮流约束。

(2)

2)节点电压约束。

(3)

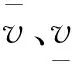
3)光储运行约束。

(4)

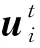
2 算法描述

本节主要阐述求解配电网时变最优潮流的相关问题，针对已有求解算法未考虑不同时间段决策值之间耦合关系的缺点，提出了一种计及电压预测的主动配电网分布式电源在线优化决策方法，首先对负荷波动后配电网潮流状态进行预测求解，然后在预测求解的基础上对时变最优潮流问题进行在线求解。本文所提在线优化决策方法实现框架如图1所示。

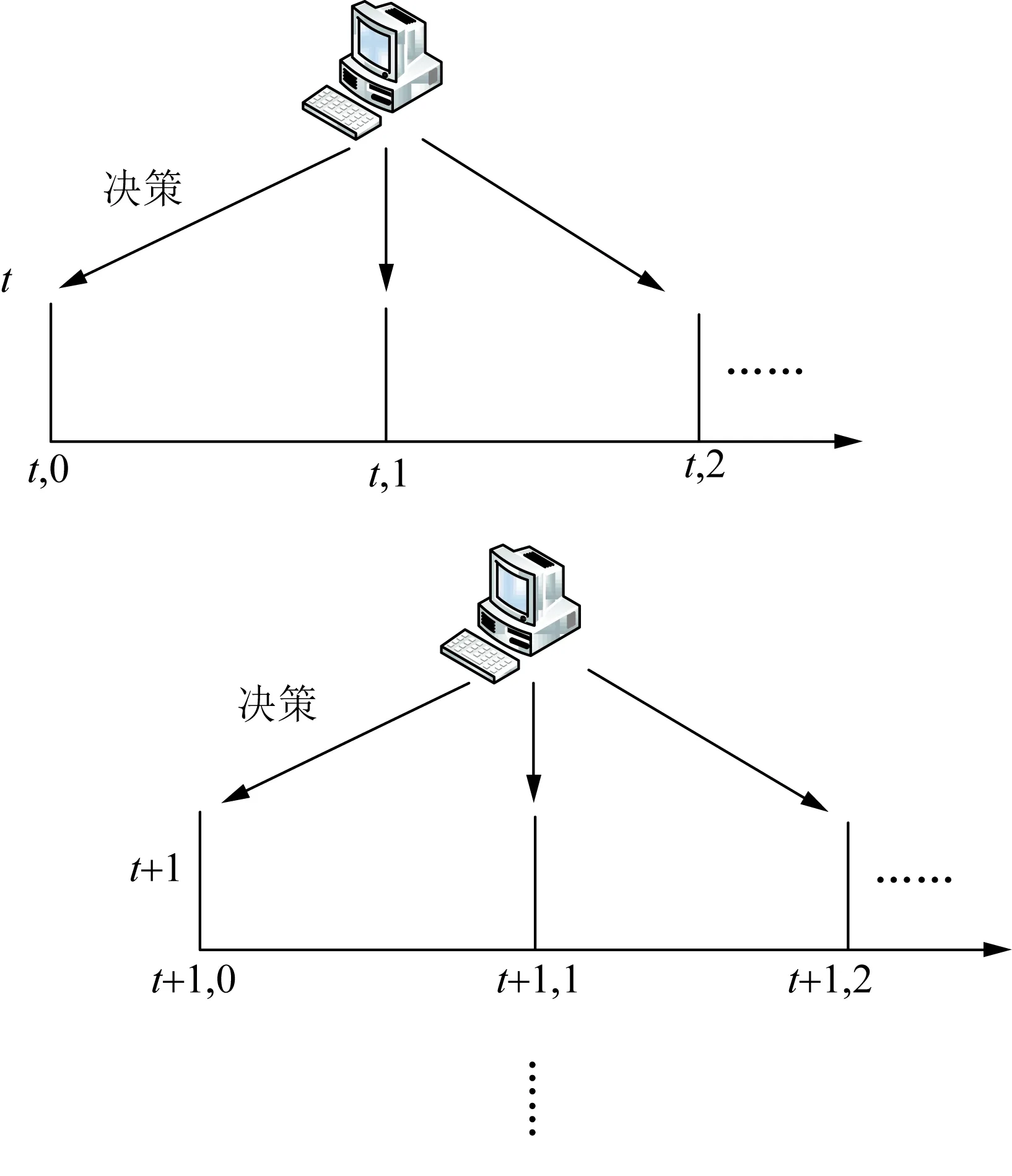
图1 在线优化决策方法框架Fig.1 Schematic diagram of the framework of online optimization decision algorithm

2.1 在线优化算法

目标函数需要在满足式(2)—(4)的基础上进行求解，基于罚函数将式(2)中的约束转移到目标函数中，构建增广目标函数：

(5)

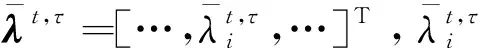
基于式(5)配电网时变最优潮流模型又可以描述为：

(6)

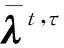
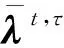
(7)

(8)

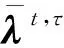
(9)

(10)

从式(6)—(10)中可知，若想求解分布式电源输出设定值，须从配电网获取负荷波动后的节点电压。利用本文所提方法预测各时段负荷波动后配电网节点电压的流程如图2所示。

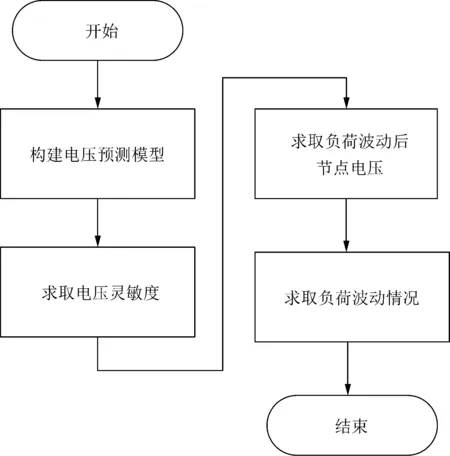
图2 预测负荷波动后配电网节点电压流程Fig.2 Flow chart of distribution network node voltage prediction after load fluctuation

2.2 节点电压预测方法

对系统的节点电压进行预测应首先构建预测模型，然后根据所构建的预测模型，求解所需参量，进而预测负荷以及分布式电源决策设定值变化后的配电网节点电压。

1)预测模型的构建。

(11)

2)预测负荷波动后的配电网节点电压。

(12)

3)预测分布式电源决策值变化后配电网节点电压。

(13)

式中：Ht为依据预测负荷波动后节点电压幅值所求取的电压灵敏度。

从式(12)、(13)中可知，灵敏度矩阵中各参量存在时间耦合关系，因此为了方便计算，对其耦合关系进行解耦。

(14)

式(14)中∂Vt,i/∂Vt,τ=1，因此式(14)又可以描述为：

(15)

将式(13)求取电压量测值的方法代入到增广目标函数式(5)中，增广目标函数又可以描述为：

(16)

利用式(16)其配电网时变最优潮流模型又可以描述为：

(17)

从式(17)可以看出配电网时变最优潮流模型只与负荷以及分布式电源输出设定值的变化量有关。

本文所提方法求取分布式电源决策设定值变化量的流程如图3所示。

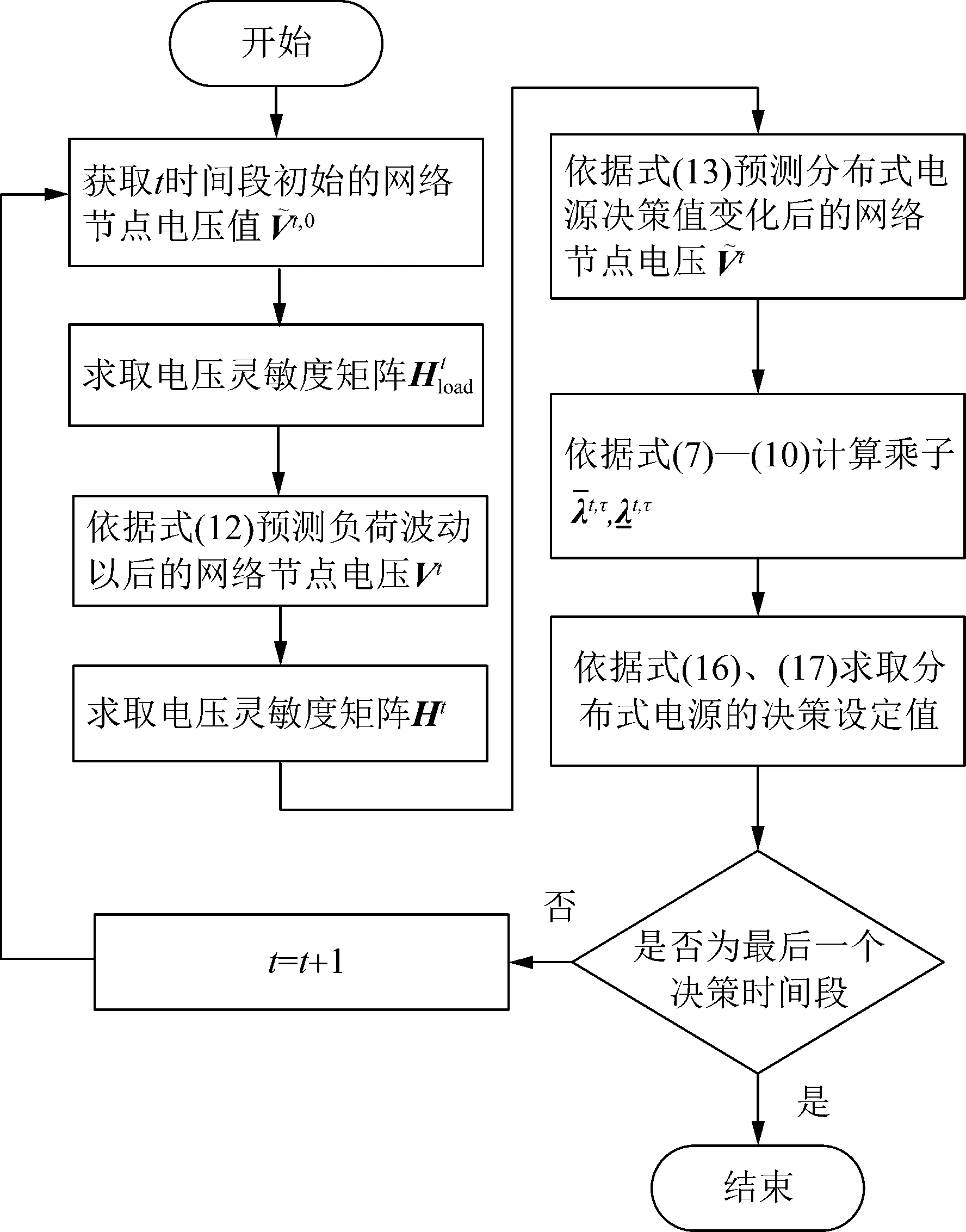
图3 所提在线优化决策方法实现流程Fig.3 Flow chart of online optimization decision algorithm

3 算例分析

在含有高比例分布式光伏电源以及储能电源的配电网中进行算例分析，以验证本文所提在线优化决策方法的有效性。

本文采用502节点配电网算例系统进行算例仿真分析，502节点配电网算例系统拓扑如附录图A1所示。算例系统中各线路参数见文献[20]。算例参数设置见表1。

表1 算例参数设置Table 1 Study parameter settings

算例系统中节点1设为平衡节点。除节点1外，其余节点均接入光伏电源以及储能电源，并且各节点所接入光伏电源以及储能电源的类型均相同，详细参数见表1。各节点负荷采用配电网的实际运行数据，负荷运行数据的时间间隔为1 s。光伏电源的初始有功功率为当前时刻分布式光伏运行的真实数据，光伏初始无功功率以及储能电源初始的有功功率、无功功率均为0。迭代步长α=0.01。目标函数系数为apv=1、bpv=0.01、ab=0.25、bb=0.01。其允许的电压上下限分别为1.05、0.95 pu，电压基准值为12.66 kV，功率基准值为1 MV·A。

3.1 在线优化决策方法求解最优潮流有效性分析

为了验证本文所提在线优化决策方法的收敛性，在各节点注入功率都已给定的13:25时刻，对目标函数L的收敛过程进行分析，分析结果如图4所示。由图4可知，本文所提优化算法在迭代过程中可以使目标函数L逐渐趋于最优值，进而验证了本文所提算法可以使目标函数达到收敛的效果。

图4 目标函数在各节点注入给定下的收敛过程Fig.4 Convergence process of the objective function under the given injection of each node

3.2 在线优化决策方法对电压控制的有效性分析

对未采用在线优化决策方法时一天的原始数据进行分析，并对各节点电压的最大、最小值进行统计，统计结果如图5所示。由图5可知，大约有3/4的节点电压会越限。

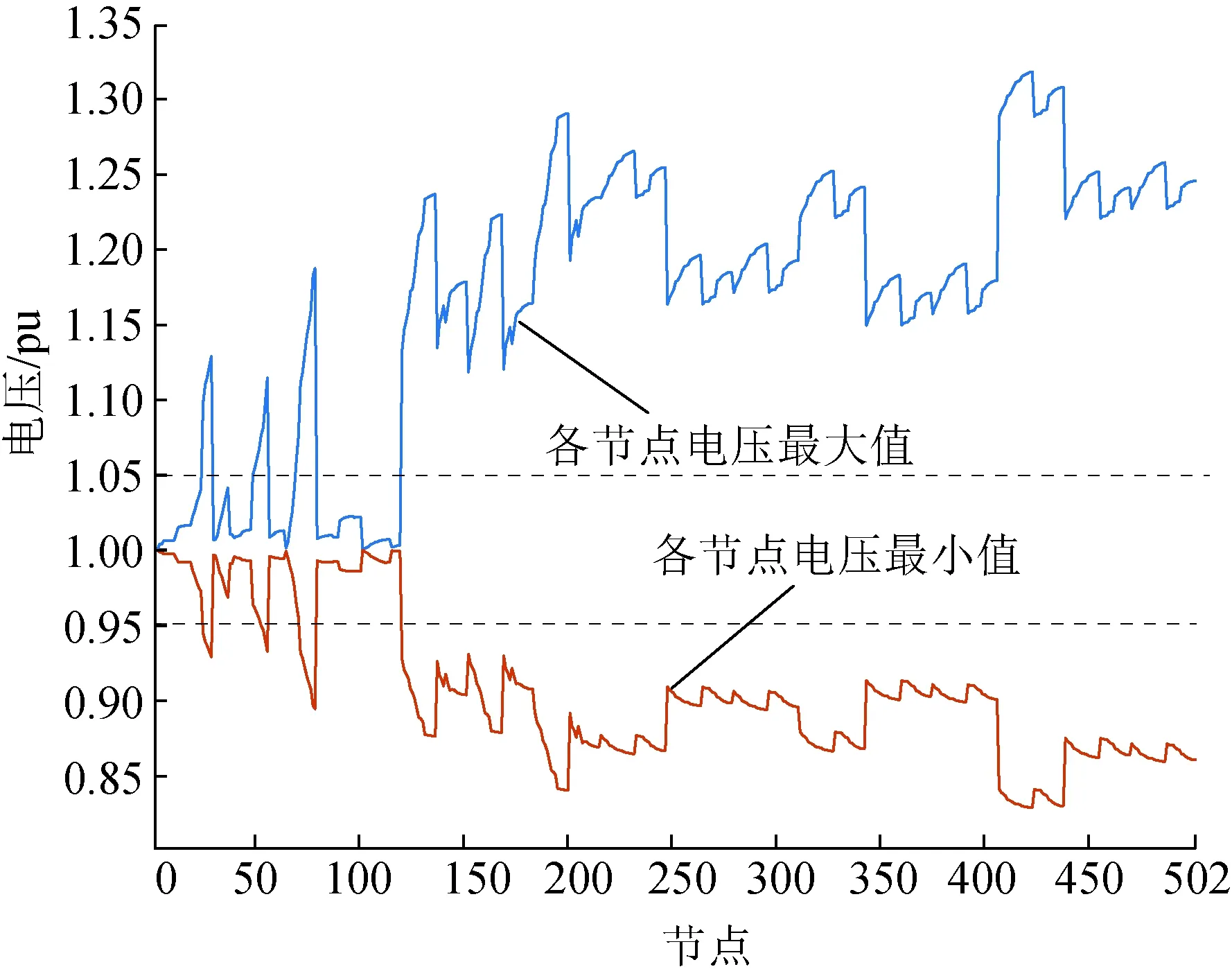
图5 配电网各节点电压的最大、最小值统计Fig.5 Statistics of the maximum and minimum voltage of each node in the distribution network

图6进一步给出了节点电压越限最严重节点(423节点)的电压幅值在一天内的变化情况。选取423节点电压越上限最严重时段13:25—13:35以及越下限最严重时间段19:55—20:05，采用所提在线优化决策方法进行优化计算。

图6 未采用在线优化决策方法423节点电压幅值变化Fig.6 Voltage amplitude change of node 423 without online optimization decision algorithm

采用在线优化决策方法后423节点在时间段13:25—13:35时的电压情况如图7所示，图7中一开始电压仍越限，是由于电压调节需要时间，通过多次迭代可以使越限电压保持在允许范围之内；在时间段19:55—20:05时的电压情况如图8所示，图8中一开始电压仍越限，仍然是因为电压调节需要时间，通过多次迭代可以使越限电压保持在允许范围之内。综上基于本文所提在线优化决策方法可以将节点电压控制在有效范围之内。

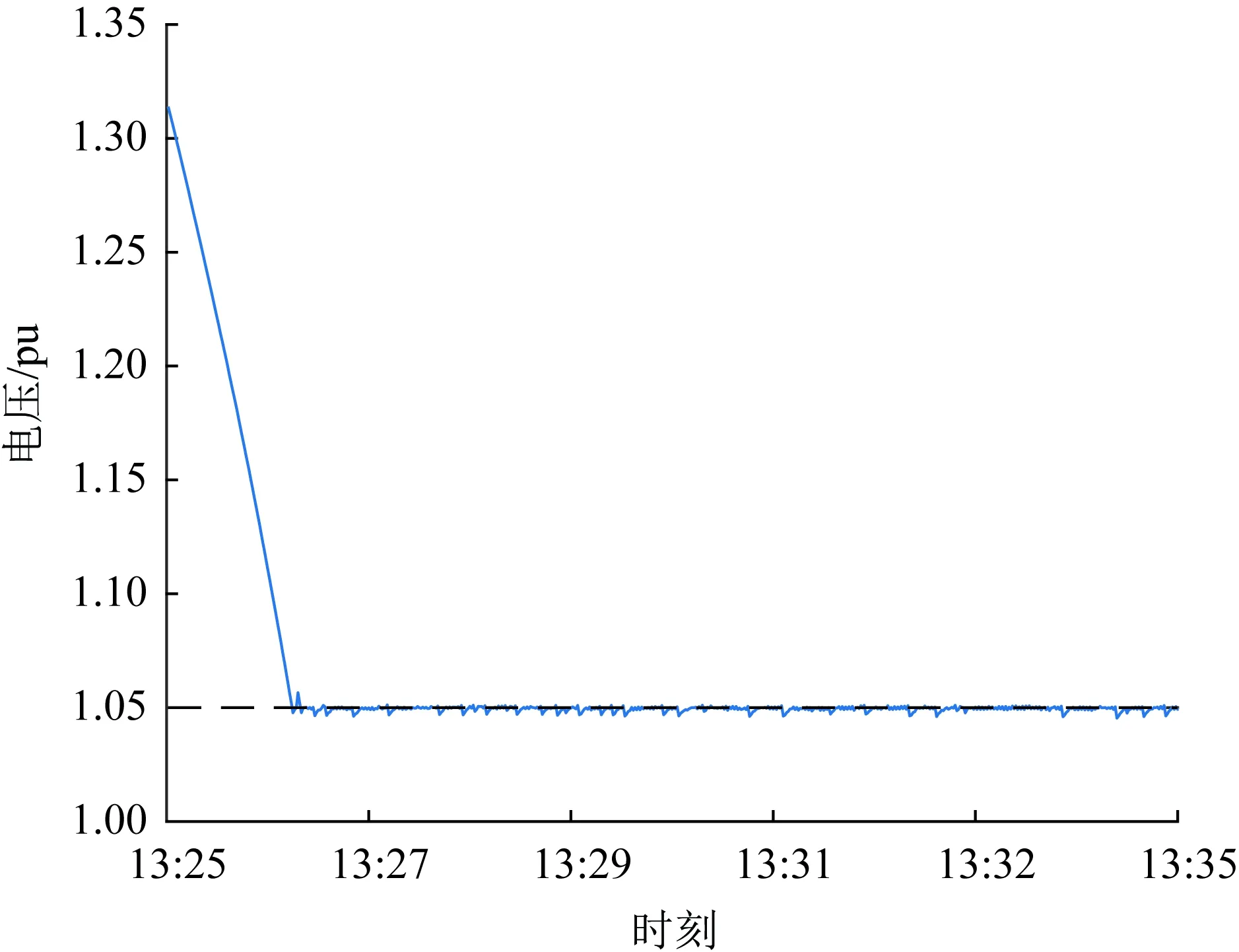
图7 采用在线优化决策方法后13:25—13:35时段423节点电压幅值变化Fig.7 Voltage amplitude change of node 423 from 13:25 to 13:35 after using the online optimization decision algorithm

图8 采用在线优化决策方法后19:55—20:05时段423节点电压幅值变化Fig.8 Voltage amplitude change of node 423 from 19:55 to 20:05 after using the online optimization decision algorithm

3.3 在线优化决策方法对储能能量变化的有效性验证

由于本文所提算法考虑了未来多个时间段的最优潮流问题，因此需要对储能的能量进行一定的约束。针对13：25—13：35时段的423节点储能电源进行分析，储能的能量变化如图9所示。由图9可知，未采用本文所提在线优化决策方法前储能的变化未考虑未来时间段对储能能量的需求，因而在能量到达一定数值后就不再进行充电。而采用本文所提优化算法后，由于储能电源考虑了未来时间段内对储能放电的需求，因此该时段储能所储存能量更多。

图9 采用在线优化决策方法前后储能电源能量变化情况Fig.9 Energy change of energy storage device before and after using the online optimization decision algorithm

4 结 论

1)针对含大量分布式光伏电源以及储能电源的配电网提出了一种时变最优潮流在线优化决策方法，该算法能够在保证各时刻各节点电压均在合理范围之内的条件下，进行时变最优潮流的追踪求解。

2)与已有的在线优化算法相比，所提的在线优化决策方法，考虑了各时段储能电源出力的耦合性。可以根据未来时间段对储能能量的需求并结合当前时间段对储能能量的需求从而制定当前时段储能电源的充放电计划。

未来，随着分布式光伏电源以及储能电源大量接入配电网，网络净负荷波动会更加剧烈。通过预测未来时段内的配电网网络节点电压可以调整各电源的输出设定值，可以有效遏制节点电压越限问题，使配电网更加稳定地运行，因此该研究具有较好的工程应用价值。