基于一次二阶矩法的折臂机构运动可靠性分析*

薛自然 冯 伟 王卫军 熊新红 王世杰,4

1武汉理工大学交通与物流工程学院 武汉 430063 2中国科学院深圳先进技术研究院 深圳 518055 3中国科学院大学 北京 100049 4河北工业大学机械工程学院 天津 300401

0 引言

搬运机器人末端执行器的运动精度问题是机器人设计制造过程中的重要问题，其精度大小直接影响着搬运作业质量，而机器人各零部件的尺寸偏差和关节间隙偏差是导致末端精度超出范围的重要原因[1]，这些偏差往往是不可控的，故会对机构末端的运动精度产生极大影响。运动可靠性表示的是机器人末端执行器在某一特定的时间内落入许用精度范围内的概率[2]，这一概念是评价这些不可控因素的一项重要指标。

许多学者对如何提高机器人末端执行器的运动精度进行了广泛的研究。孙志礼等[3]通过ADAMS软件建立3-RPS并联机器人的参数化虚拟样机模型，在考虑杆长误差和球副误差的作用下通过蒙特卡洛法计算得出了机器人的运动可靠度；Du X P[4]通过建立包络线的方法，对典型四杆机构进行动态运动可靠性的求解；李怀政等[5]通过ADAMS仿真软件，基于蒙特卡洛法对SCARA机器人机构运动可靠性进行研究。Zhang J F等[6]提出了一种混合降维法，实现了在机械装置关节的随机间隙影响下的运动可靠度的分析；文瑞桥[7]考虑关节参数的不确定性，采用一次二阶矩法计算求得了斯坦福机器人末端执行器的运动可靠度。

图1是一款正在设计制造阶段的新型幕墙搬运机器人，其中框选部分即为折臂机构。搬运机器人在幕墙搬运作业中载荷较大，移动底盘倾斜、传动环节间隙、液压缸尺寸误差等因素均会导致机器人末端存在柔性，从而导致作业不确定性，这不仅会影响到搬运机器人作业的质量与效率，甚至会由于末端位置的偏差而导致搬运机器人的倾覆以及末端执行器上所吸附的幕墙的碎裂，因此，提高该款搬运机器人的运动精度，对该款机器人能否真正应用在实际作业中起着决定性作用。

图1 折臂机构在幕墙安装机器人上的应用

本文针对该款机器人的折臂机构进行分析，考虑折臂机构驱动装置液压缸的尺寸偏差对系统准确度的影响，在对该机构的运动学正解求解的基础上，对其进行微分得到位姿输出误差模型，然后应用一次二阶矩法求解机构的运动可靠性，最后通过蒙特卡洛法验证这一结果。

1 机构描述

如图2所示，折臂机构由基平台、2个支臂、3个液压缸推杆机构、末端执行器平台等部分组成。除了每个液压缸推杆机构是通过滑动副连接，其他各部分之间均通过转动副进行连接，3个液压缸为机构原动件，折臂机构具有3个自由度。

图2 折臂机构模型

折臂机构运动简图如图3所示，全局坐标系为{O}设在基平台中心点，取竖直向上为z轴正方向，垂直纸面向里是y轴正方向，水平向右为x轴正方向。A～I分别代表折臂机构各个转动副，J为折臂机构末端执行器位置。

图3 折臂机构运动简图

2 机构建模

2.1 运动学求解

针对折臂机构进行正运动学分析，首先将液压缸看作一个整体，假设液压缸BC、EF、HI的整体长度分别为x1、x2、x3，该长度随活塞杆行程的变化而不断变化。

如图3所示，坐标轴原点位置、x轴方向、y轴正方向和各点位置均已给出，则在ΔABC、ΔDEF、ΔGHI中有

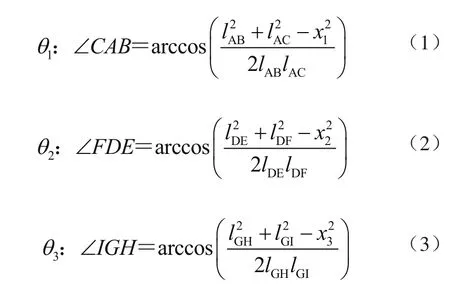
在图3中，已知∠BAx、∠CAD，则有

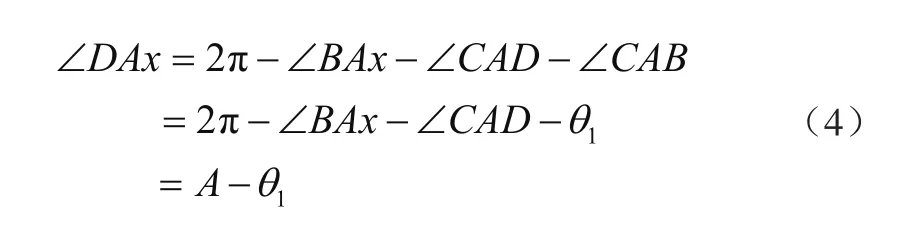
A点坐标已知，假设为(xA，zA)，AD长度已知，为lAD，则D点坐标为

在图3中，已知∠ADE、∠FDG，则有

已知DG长度为lDG，则G点坐标为

在图3中，已知∠DGH、∠IGJ，则有

已知GJ长度为lGJ，则J点坐标为

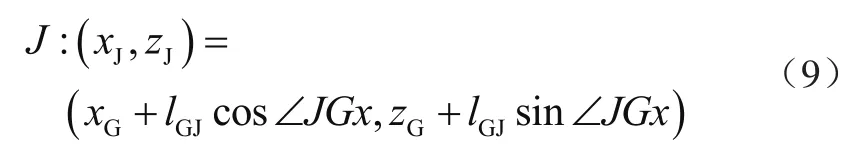
式（9）即为折臂机构运动学正解函数式。

2.2 误差分析与建模

常用的误差建模方法有微分法、摄动法、矢量法等，这里选用微分法对末端执行器偏差进行建模，根据运动学模型，x1、x2、x3的误差Δx1、Δx2、Δx3会对机器人末端执行器的位置产生影响，从而使末端执行器偏离其原始位置坐标。误差建模就是要建立各原始误差与末端执行器位置误差之间的函数关系。

由式（9）可建立折臂机构运动学方程为

式中：J为末端执行器坐标；xi为各输入参数；i为输入参数数量，i=1、2、3。

根据微分法，对式（10）两端分别求导，各原始误差传递系数为末端执行器位置坐标依次对各原始误差参数求偏导，依此可建立末端执行器的位置误差函数关系式为[8-10]

式中：ΔJj为折臂机构末端执行器位置偏差，j为末端执行器坐标方向数量，Δxi为各原始误差参数，Jp为末端执行器位置误差与各原始误差之间的误差传递系数雅可比矩阵。

误差传递系数雅可比矩阵可表示为

进一步整理可得

2.3 系统可靠性建模

运动可靠性是评价机构运动精度高低更本质的评价指标。对机构进行运动可靠性分析，即希望在机构设计之初就可以得到，在各原始误差影响下，批量生产的机构中任意一台其末端执行器运动误差落入许用范围内的概率[11]。从而发现机构中的不稳定部分，为之后机器人运动精度的提高提供指导。

一次二阶矩法(FOSM)作为分析运动可靠性的常用方法，是通过分析末端执行器误差函数的一阶矩和二阶矩来实现对机构运动可靠性的分析方法。其通过确定原始误差的一阶矩和二阶矩，推导出末端执行器误差的一阶矩和二阶矩，从而实现对末端执行器的可靠性的分析[12]。针对单一变量类型可靠性分析，一次二阶矩法往往具有较高的精度[13]，本文选用一次二阶矩法对机构运动可靠性进行分析。

假设之间相互独立，且是正态分布的随机变量，即

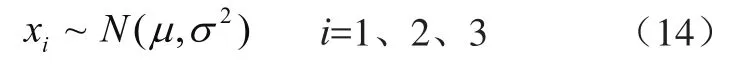
且因为

其中，Ui~N(0，1)，故可知液压缸尺寸误差符合正态分布

根据式(11)、式(16)可得

由正态分布函数变换规律可知，正态分布函数乘以一个系数后仍为正态分布，即折臂机构末端执行器误差ΔJ也符合正态分布，根据式(15)～式(17)可知，ΔJ均值为0、末端执行器误差ΔJ所符合的正态分布函数的标准差为

设折臂机构末端执行器的允许误差范围为ε，根据可靠性概念，在某一姿态下，某一个输入误差参数的可靠度R(Δxi)为

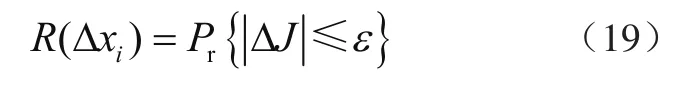
Pr｛·｝代表概率，其相应的失效率为

应用一次二阶矩法来计算串并联机构末端执行器在x、y、z方向上的可靠度，表示为[14]

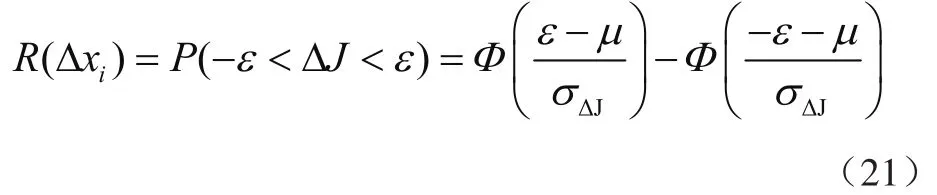
化简后得

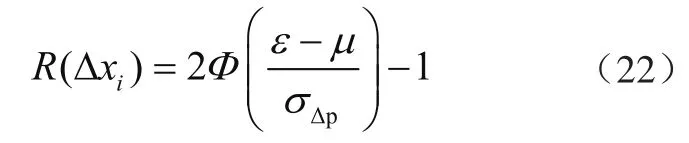
式中：Φ（·）是标准正态分布函数。

相应地，Φ（·）的失效率为

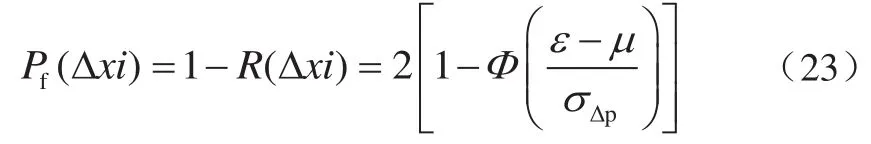
3 可靠性分析

将折臂机构的具体结构参数数据带入正运动学分析计算公式，结合式(9)、式(13)，并取折臂机构姿态为图3所示姿态，带入可求得误差传递系数雅可比矩阵为

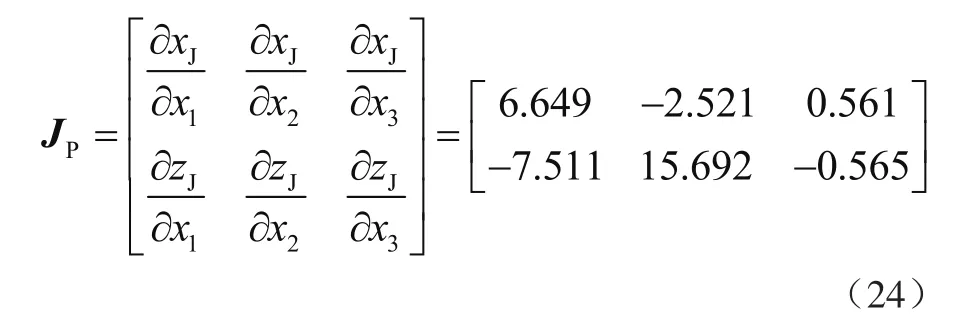
由于x1、x2、x3初始长度依次为145 mm、215 mm、230 mm，其制造加工精度一般可达IT10～IT7，通过查找公差表，取杆长标准差为

根据3σ原则，此时原始误差基本符合实际公差带的情况。

依次取Δx1、Δx2、Δx3为唯一变量，带入式(13)、式(18)、式(24)，即可得到折臂机构末端执行器在各原始误差影响下，在x、z方向上的误差所符合的正态分布的标准差（取绝对值）为

根据市面上常见折臂机构所能达到的末端执行器精度范围，取折臂机构末端执行器允许误差范围ε=0.5 mm，根据式(21)、式(25)，即可得出折臂机构在各原始误差影响下的末端执行器位置偏差的可靠度和失效率分别如图4和图5所示。

图4 末端位置偏差可靠度

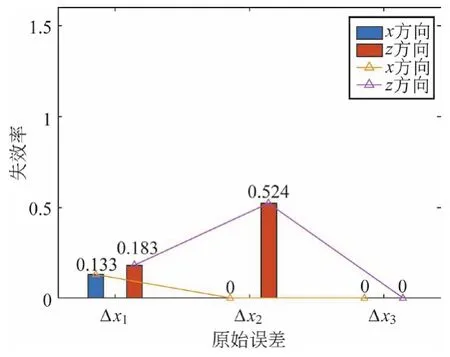
图5 末端位置偏差失效率

由图4、图5可知，原始误差参数Δx1、Δx3对折臂机构末端执行器的位置偏差影响较小，其可靠度高、失效率较低；但原始误差参数Δx2对末端执行器的位置偏差影响较大，极易导致末端执行器偏离预定坐标，从而影响搬运作业质量。因此，该可靠性分析结果表明，要保证折臂机构末端执行器的运动精度，需严格控制原始误差Δx2。

4 虚拟样机仿真分析

4.1 可靠度计算

Monte Carlo模拟法（MCS）作为求解系统可靠性最重要的方法之一，具有方法简单、适用性广、结果准确等优点，能够对任意模型的运动可靠性进行精确求解[15]，其通过计算机技术生成一组符合设定的正态分布的随机误差抽样数据，依次带入模型进行计算，即可得到折臂机构末端执行器偏差为

式中：J*为实际坐标值，J为理想坐标值。

设机构误差允许值范围为[-ε，ε]，则当∣ΔxJ∣＜ε时，代表可靠；当∣ΔxJ∣＞ε时，代表不可靠。

当模拟次数n足够大时，通过MCS方法计算机构的运动可靠度即可表示为

式中：n为总的模拟次数，s为可靠的次数。

失效率为

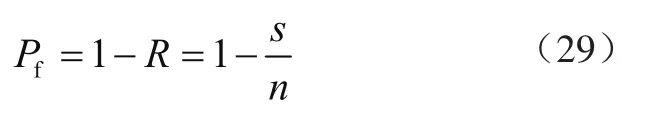
4.2 实例分析

根据图3折臂机构运动简图，在ADAMS/View内建立折臂机构模型如图6所示。

图6 折臂机构虚拟样机模型

利用Matlab软件中的Normacdf函数，根据式(16)与式(25)给定的误差均值与方差，由概率统计方法构造1 000组符合正态分布的误差数据作为折臂机构的误差样本。将样本中参数依次带入图6的ADAMS仿真模型中进行仿真，记录机构位姿输出误差。可统计得到折臂机构末端执行器位置误差可靠次数s如表1所示。

表1 末端执行器偏差可靠次数

将表1数据与n=1 000一并带入式（28）、式（29），可得出在各原始误差影响下的末端执行器位置偏差的可靠度和失效率，分别如图7和图8所示。

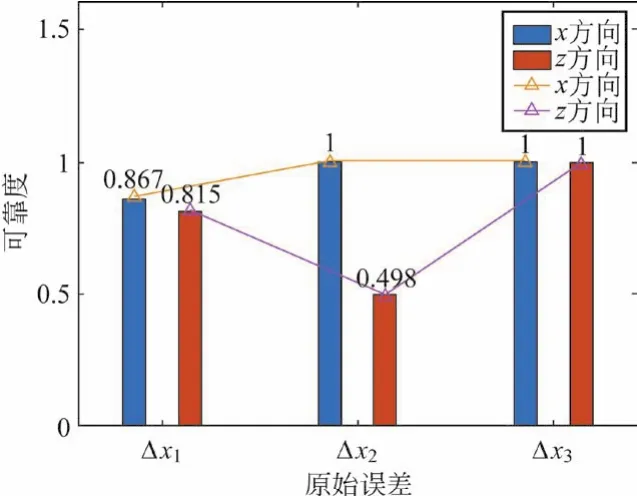
图7 末端位置偏差可靠度

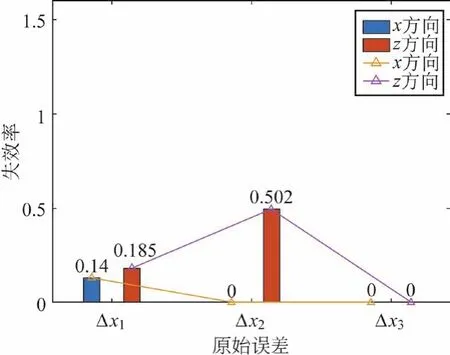
图8 末端位置偏差失效率

对比图4与图7，一次二阶矩法计算的结果与MCS方法计算的结果非常接近。但结果仍存在微小的误差，原因包括：1）一次二阶矩法仅考虑了原始误差与末端执行器偏差之间函数式的一阶偏导，其模拟精度有限；2）MCS抽样次数未趋于无穷大，故也会存在一定的误差。但对照结果可知，计算偏差控制在一定范围内，即可靠度的计算结果是准确的。

5 结论

1)通过对搬运机器人中的折臂机构进行运动可靠性分析，得知原始误差参数对机构末端执行器运动精度影响最大，为搬运机器人后续结构优化设计及末端执行器精度提高提供了优化方向和理论依据。

2)通过基于蒙特卡洛法的仿真分析方法，验证了一次二阶矩法在分析折臂机构末端执行器运动可靠性问题上的准确性。

3)本文分析对其他机器人及机构的运动可靠性分析具有一定的参考与借鉴意义。