基于时空分割的三维动画压缩算法研究
易 茹
(安徽工贸职业技术学院,安徽 淮南 232007)
0 引言
三维动画的发展对三维动画技术提出了更高要求,特别是三维动画数据应用规模的不断扩大,对三维动画压缩方法的研究成为许多学者关注的焦点。杜洪等在对主成分分析的基础上提出了一种新的算法来提取图像的主成分,并将其应用于图像压缩中,通过仿真试验验证了所提出的算法在求取主成分的时候迭代次数少、效率高[1]。罗国亮等对三维动画数据结构化方法进行研究,提出了一种新的三维动画数据压缩算法,通过动画数据结构化子块尺寸优化使得算法的时间性能大大提升,同时对图像压缩算法量化矩阵的优化满足了在相同压缩比下对准确度的要求[2]。杜博等根据K-L变换的原理找到了用于图像压缩的投影矩阵,提出了基于张量主成分分析的人脸图像压缩算法,并通过在人脸数据库中人脸图像的压缩,试验验证了该算法相对于常规的主成分分析法对人脸图像的压缩更具明显优势[3]。主成分分析法作为一种有效地实现数据降维、去冗余的算法,在图像压缩中具有十分广泛的应用,但是直接应用于三维动画压缩中效果并不理想[4]。基于此,拟将时空分割与主成分分析相结合,以实现对三维动画的有效压缩。
1 理论基础
1.1 主成分分析
主成分分析是通过正交变换将可能存在相关性的变量转换为不相关变量的统计方法,通过进行主成分分析能够达到降维、去冗余的目的。采用主成分分析进行图像压缩是将图像分块,每一块作为一个样本向量,计算样本向量协方差矩阵C的前k个比较大特征值所对应的特征向量作为主成分,同时舍弃特征值比较小的,从而达到对图像压缩的目的[5]。设样本矩阵为
X=[x1,x2,…,xn]∈Rm×n
(1)
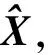
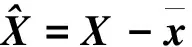
(2)
式中:
(3)
计算协方差矩阵C,即[6]
(4)
计算协方差矩阵C的特征值和特征向量,并将特征值进行降序排序,获得前k个最大特征值所对应的特征向量,分别为v1、v2、…、vk,将k个特征向量组成矩阵B,即
B=[v1,v2,…,vk]
(5)
那么原始数据X的降维矩阵Y表示为
Y=X×B
(6)
1.2 时空分割
设F为三维动画,其包含t帧动画矩阵(f1,f2,…,ft)。动画矩阵由三角形与顶点矩阵所构成,先将三角形矩阵全部转化为顶点矩阵,那么动画矩阵就转变为纯顶点矩阵。每一帧图像的纯顶点矩阵可以表示为一个m×n的矩阵,因此可以将三维动画以列作为标准进行合并,最终得到(m×(n×t))的顶点矩阵D[7]。对顶点矩阵D进行主成分分析,提出主成分以达到对三维动画进行压缩的目的。图1为三维动画压缩算法流程。

图1 三维动画压缩算法流程
定义三维动画区域在时间与空间范围内一致的为刚性区域,三维动画区域在时间与空间范围内不一致的为动态区域。采用主成分分析进行三维动画压缩时必须要考虑刚性区域与动态区域的不同,否则会导致三维动画压缩的效果比较差。
2 时空分割的三维动画压缩
2.1 创建顶点矩阵
由于三维动画矩阵由三角形矩阵和顶点矩阵所构成,需要将其全部转化为纯顶点矩阵vi。由于三维动画帧在空间上是一致的,因此可以将动画帧进行拼接,从而得到矩阵V=(v1,v2,v3)。对三维动画进行压缩的基础矩阵RS为
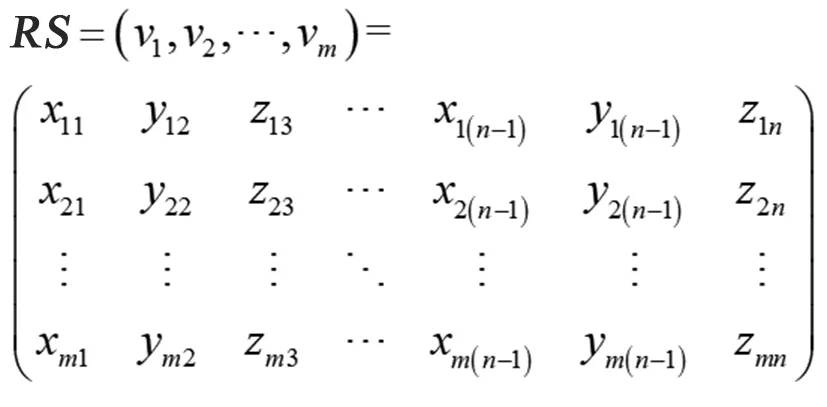
(7)
2.2 创建动态分割块
时空分割是时间域和空间域的分割,在获得顶点矩阵之后,该矩阵的横向为时域,竖向为空间域,顶点矩阵示意如图2所示[8]。
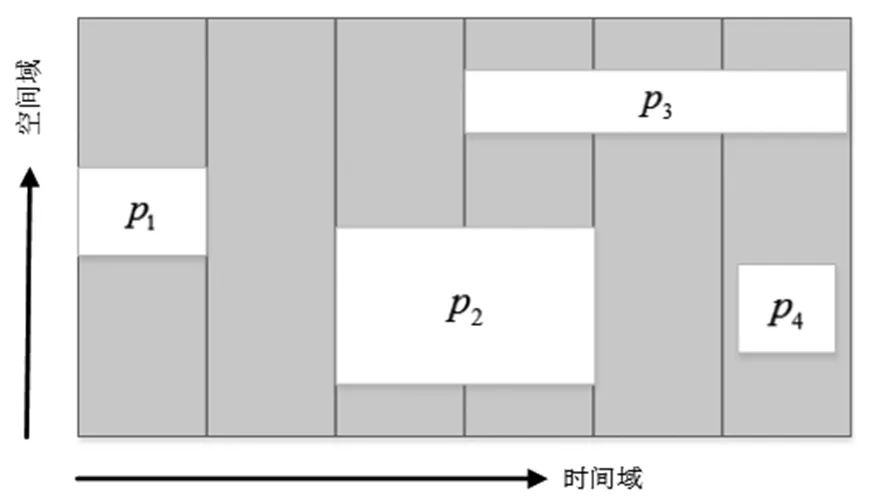
图2 顶点矩阵示意
在图2中,灰色的方块为动画帧数据,p1、p2、p3、p4为时空分割块。根据动画跨域分割算法能够得到动态分割块在基础矩阵RS中所对应的位置,记为StSi。很明显,矩阵StSi为基础矩阵RS的子矩阵,其为图2中的白色方块。StSi在时间上是跨域的,时空分块p1和p4在同一个动画帧,且p4不满一个动画帧,时空分块p2和p3跨越多个动画帧。
2.3 刚性区域
刚性区域顶点矩阵的构造需要在基础矩阵RS中寻找到动态分割块顶点矩阵StSi所对应的分块,使得分块元素被替换为一致性比较好的值。定义RS′为刚性区域顶点矩阵,那么分割静态区和活动区的关键是判断那些数据需要分割,活动区数据往往和矩阵的整体具有比较大的差别。
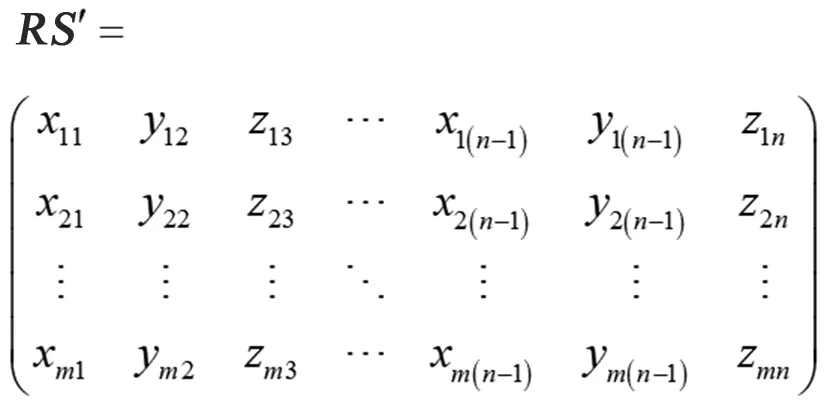
(8)
为了区分静态区和活动区,设置考量活动区或者静态区(刚性区)的阈值τ。如果数据的区别超过了设定的阈值τ,那么就可以判定为活动区[9]。
三维动画动态分割之后进行图像压缩,同时剩余的刚性区也需要进行图像压缩,而此时由于动态分割动态区是空白的,因此必须对动态区域进行填补。由主成分分析的原理可知,一致性高的数据,其主成分的维度小,可以大大提高压缩的效率。因此采用剩余刚性区域均值来对动态区域进行填补,即
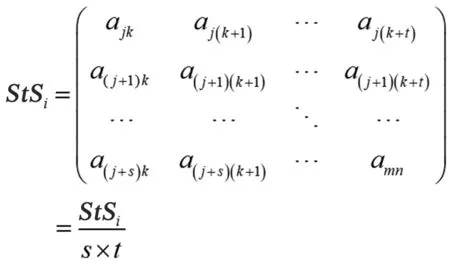
(9)

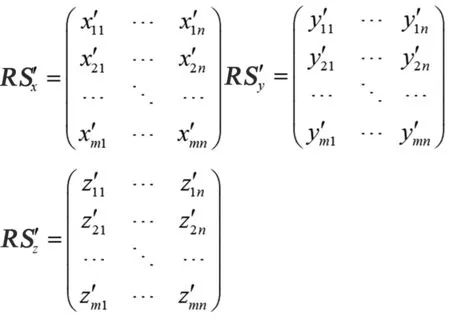
(10)
2.4 三维动画压缩流程
三维动画划分为活动区和刚性区,对刚性区采用主成分分析进行压缩处理,活动区域进行动态分割。另外,考虑不同维度数据离散导致采用主成分分析对图像压缩性能的不利影响,对刚性区域进行维度分割,这样就可以将空间3个不同维度的数据组成3个时空分割矩阵。采用主成分分析法对3个时空分割矩阵进行分析,同时对动态分割块也采用主成分分析法,从而实现对三维动画的压缩。基于时空分割的三维动画压缩算法流程如图3所示。
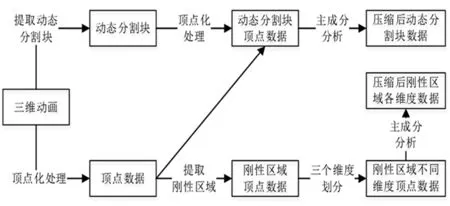
图3 基于时空分割的三维动画压缩算法流程
3 实例分析
3.1 试验数据
选择4个动画进行三维动画压缩效果的仿真分析,4个动画的顶点数、面片数、帧数信息如表1所示。
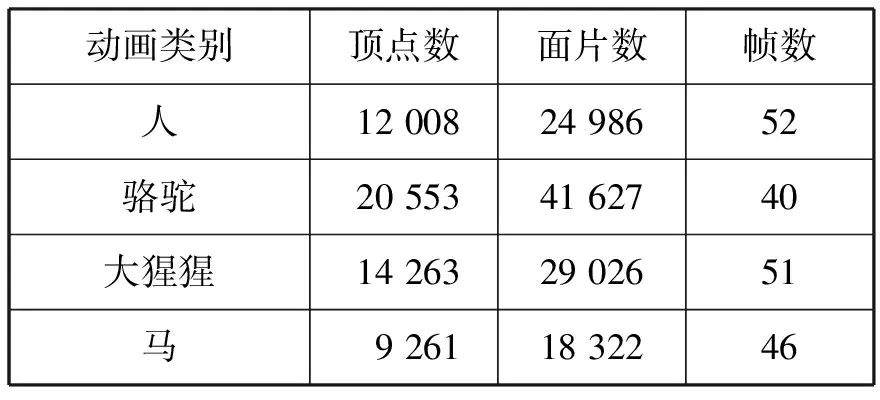
表1 4个动画数据信息
设置考量活动区或者静态区(刚性区)的阈值τ=0.65,采用基于时空分割算法分别对动态分割与刚性分割应用主成分分析法(方法1)、基于时空分割区分3个维度应用主成分分析法采用动态分割与刚性分割压缩法(方法2)对2种三维动画压缩,对比2种方法对三维动画的压缩性能。对三维动画压缩性能的评价指标为压缩比γ和误差Rrror,其数学表达式为[10]
(11)
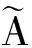
三维动画压缩算法的压缩比越低,其压缩效果越好;压缩比越高,其压缩效果越差。三维动画压缩算法的误差率越低,其压缩效果越好;误差率越高,其压缩效果越差。
3.2 结果分析
采用2种算法对4个三维动画进行压缩仿真试验,结果如图4所示。
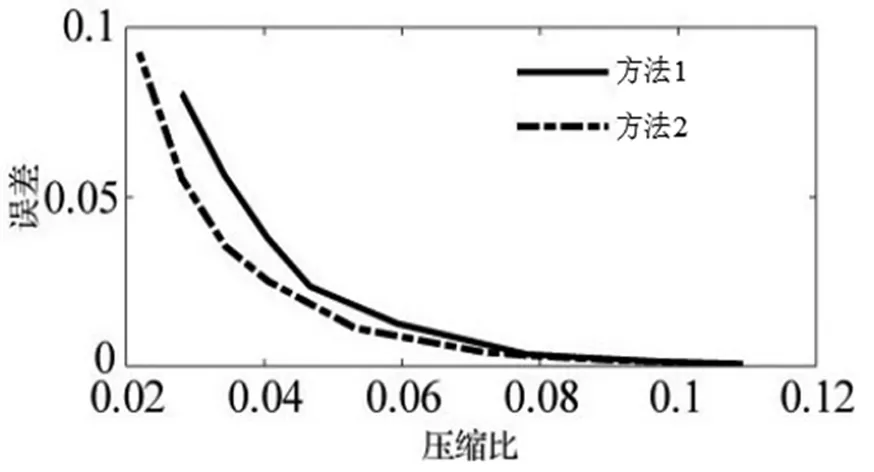
a) “人”三维动画压缩仿真结果
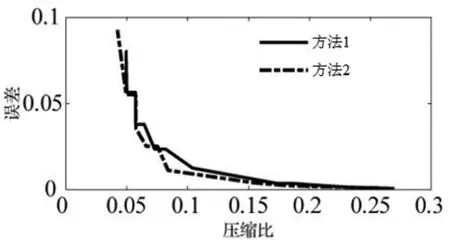
b) “骆驼”三维动画压缩仿真结果
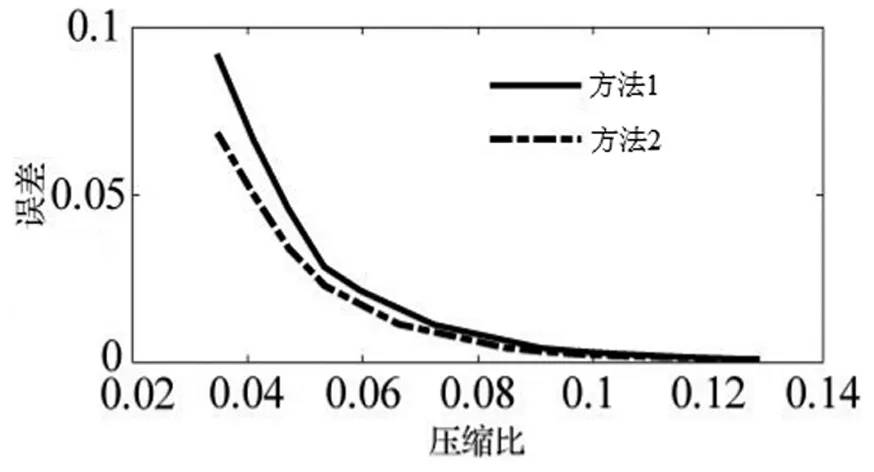
c) “大猩猩”三维动画压缩仿真结果
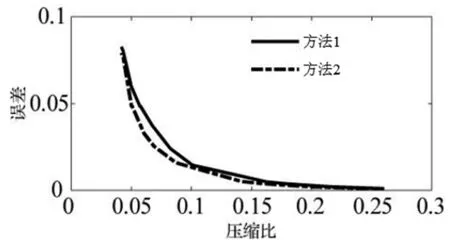
d) “马”三维动画压缩仿真结果
由图4可知,动画序列往往比较长,这使得其动态冗余信息量比较大,提取动态分割并进行压缩往往能够取得更好的压缩效果。另外,当压缩比较小时,方法2的误差比方法1的误差小,具有更好的压缩效果。这是因为在压缩比较大的情况下,空间数据不同维度独立进行压缩时往往能够得到更加充分的主成分维度需求,从而使得各个维度具有更加良好的还原效果。
4 结论
针对三维动画数据量大,冗余信息多导致三维动画分析、传输、存储困难等问题,对三维动画压缩算法进行了研究。对三维动画进行跨域时空分割以及维度划分,刚性区域采用主成分分析算法进行压缩处理,活动区域进行动态分割,同时对动态分割块采用主成分分析法。将其应用于4个三维动画的压缩仿真试验中,结果表明,基于时空分割的三维动画压缩算法能够对三维动画取得良好的压缩效果。

