一种基于柔性装置的配电网网架结构设计与研究

肖文浩，彭卉，刘兴栋，赵理，张程柯

（1.国网重庆市区供电公司，重庆 400010；2.国网重庆市电力公司，重庆 400010）

0 引言

随着社会经济的发展和分布式能源的广泛接入，对供电可靠性和供电质量的要求也越来越严格，提高电能传输效率和能力的方法和技术也不断涌现[1-3]。由于电力电子器件及控制技术的迅速发展，采用基于功率半导体器件的电力电子技术是实现配电网功率优化控制和分布式能源并网的新技术手段[4-6]。基于功率半导体器件的柔性设备可以高效可靠地实现电网电能变换和大小调节，实现分布式能源的即插即用[7-8]。

根据换流器特性，基于功率半导体器件的换流器拓扑可以分为电流源换流器（current source converter，CSC）和电压源换流器（voltage source converter，VSC）两大类。目前，应用于电网功率控制和电能传输领域的换流器拓扑大都是基于晶闸管的电网换相换流器（line commutated converter，LCC）。LCC 采用大功率晶闸管器件级联，具有结构简单、造价低、可靠性高、技术成熟、损耗小等优点[9-11]。然而，由于晶闸管是半控型器件，即只能控制开通不能控制关断，LCC 存在交流电压谐波大、功率因数低、逆变侧换相失败等缺点[12-13]，并不适合功率需要灵活控制的配电网系统。

相较于LCC，基于全控型功率半导体器件的电流源换流器（CSC）同样具有结构简单、造价低、损耗小、穿越交直流故障能力等优点[14-16]。CSC 目前已广泛应用于船舶电机驱动和风力发电系统，但尚未见CSC 应用于配电网系统。目前关于CSC 的控制策略研究已经成熟，但学者提出的控制策略基本采用定直流电压控制，并不能实现CSC 的全功率范围单位功率因数运行[17-18]。

相较于CSC，由于电压源换流器（voltage source converter，VSC）能够功率四象限运行、有功功率和无功功率完全解耦，且输出的交流电压谐波含量少、交流侧滤波设备简单，VSC 在配电网功率控制领域的应用也更加广泛。目前，VSC 拓扑主要有两电平VSC、三电平VSC 及模块化多电平换流器（modular multilevel converter，MMC）结构。两电平或三电平VSC 结构简单、损耗低、控制技术成熟，但由于直流侧并联有滤波电容，不具备直流短路故障穿越能力[19-20]。MMC 由于桥臂采用功率模块级联，具有模块化结构、输出交流电压谐波含量低、冗余设计、鲁棒性强等优点[21-23]。但为了穿越直流故障，需要有能够输出负电压的功率模块，需要大量的功率半导体器件和模块电容，存在造价高、损耗大的缺点。因此，两电平或三电平VSC 和MMC 并不适用于配电网功率控制系统或实现分布式能源并网。

前述CSC 和VSC 均是仅能够实现AC/DC 或DC/AC 变换的拓扑，而为了实现光伏、电动汽车、储能电池等直流负荷的有效利用，需要一种能够实现DC/DC 变换的换流器拓扑，即DC/DC 换流器。根据功率大小和电压等级的不同，学者们也提出了不同类型的DC/DC 换流器拓扑。文献[24]提出了一种高压侧串联低压侧并联的级联有源桥结构拓扑，文献[25]提出了一种模块化直流链接固态变压器结构拓扑。文献[24-25]提出的拓扑结构都是以双有源桥（dual active bridge，DAB）结构为基本组成单元，需要大量的功率半导体器件和高频变压器。文献[26]提出一种基于模块化多电平换流器的（modular multilevel converter，MMC）front-to-front 结构DC/DC 换流器，该换流器交流侧采用工频变压器连接。文献[27]提出交流侧采用LCL 结构和高频梯形波调制策略的基于MMC 的DC/DC 换流器结构。然而，由于采用模块化结构，文献[26-27]提出的DC/DC 换流器成本很高，损耗较大。

综上所述，为了发挥CSC 和VSC 的优势，同时实现配电网的功率控制和分布式电网的有效并网，本文提出了一种基于CSC 和VSC 的交直流智能配电网网架结构。通过CSC 连接不同交流配电网系统，可以实现功率在不同配电网系统中的优化分配，避免了配电网重载的出现。同时，为了实现分布式直流电源或负荷的并网发电，本文提出了一种基于CSC 和VSC 混合的DC/DC 换流器。本文提出的交直流配电网架构控制简单且成本较低。为了实现换流器的单位功率因数运行，本文提出了配电网架构中某端交流配电网CSC 定直流电流控制，其余端交流配电网CSC 定有功无功功率控制，混合DC/DC 换流器定直流电压控制的综合控制策略。通过改变有功功率参考值或直流电压参考值即可实现配电网功率控制或分布式能源并网功率。

本文首先介绍了提出的交直流智能配电网架构，分析了交直流配电网系统的数学模型。基于数学模型，提出了适用于交直流智能配电网系统的控制策略。最后，在Matlab/Simulink 仿真软件中搭建了基于柔性装置的交直流智能配电网系统仿真模型，对本文提出的网架结构和控制策略进行了仿真验证。

1 交直流智能配电网网架结构

提出的基于柔性装置的交直流智能配电网网架电路结构见图1，其中配电网通过CSC 连接，分布式直流电源或直流负荷通过混合DC/DC 换流器并入直流电网，分布式交流电源或负荷通过CSC 并入直流电网。

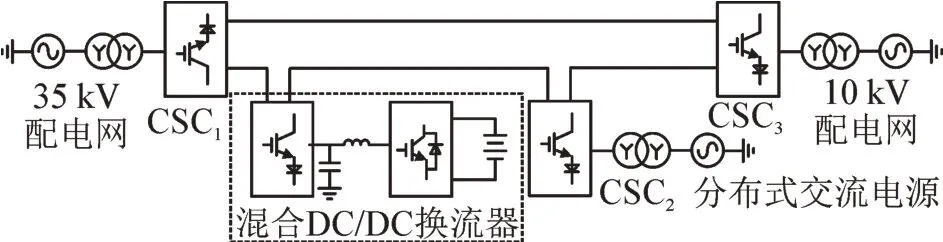
图1 交直流智能配电网网架结构电路原理图Fig.1 Circuit principle diagram of AC-DC intelligent distribution network

系统中的配电网通过CSC 互相连接，由于35 kV配电网侧CSC 采用定直流电流控制，其直流侧承受较大的直流电压，故采用多个CSC 直流侧串联、交流侧并联的结构，电路原理图见图2。

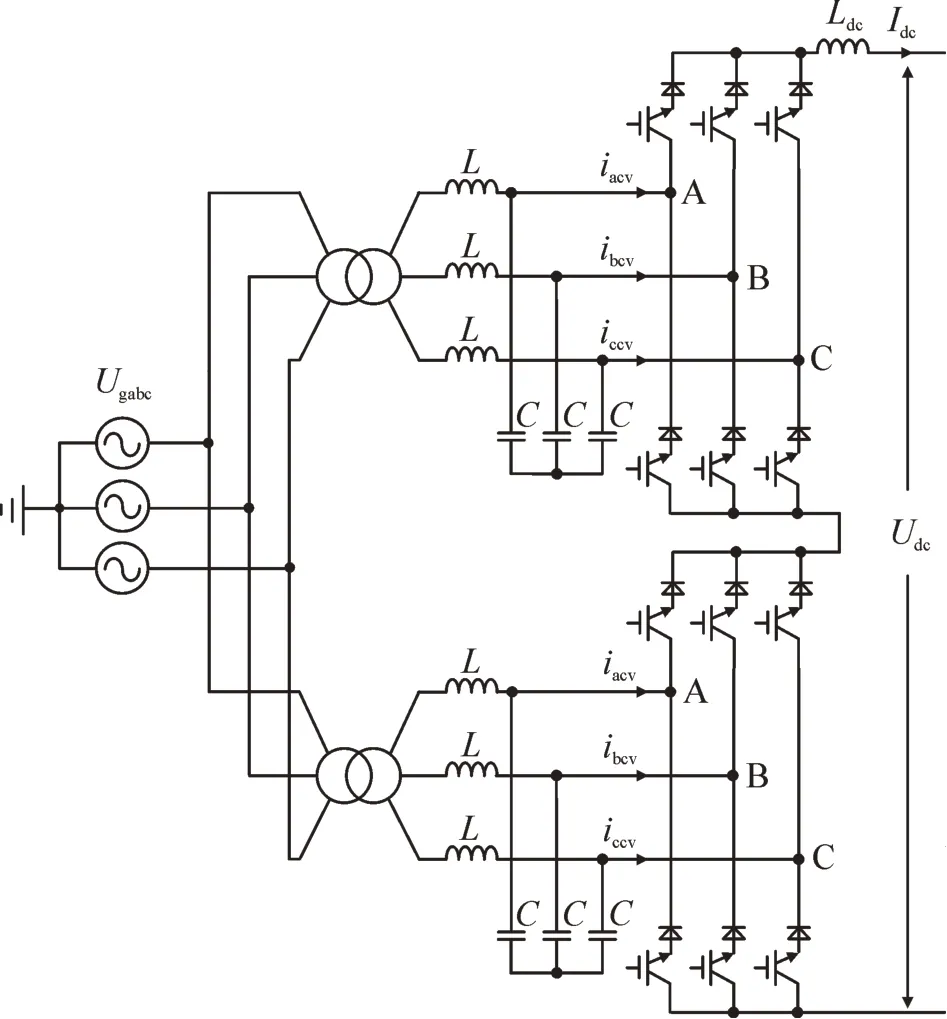
图2 35 kV配电网侧CSC电路拓扑Fig.2 Circuit topology of CSC at 35 kV distribution network side

10 kV 配电网侧CSC 的电路结构见图3，采用传统的两电平结构。

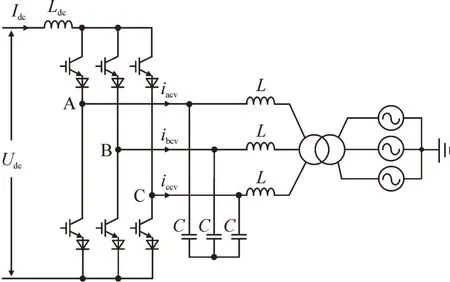
图3 10 kV配电网侧CSC电路拓扑Fig.3 Circuit topology of CSC at 10 kV distribution network side

系统中的直流电源或负荷通过提出的基于CSC-VSC 的混合DC/DC 换流器拓扑实现并网，其中直流电网侧采用CSC，直流负荷侧采用VSC，见图4。由于VSC 直流侧并联有大电容，可以实现直流负荷的电压控制。

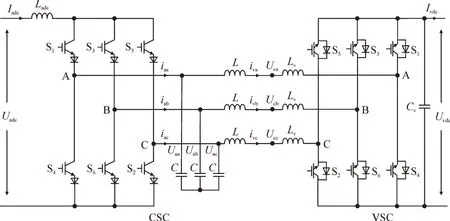
图4 混合DC/DC换流器电路拓扑Fig.4 Circuit topology of hybrid DC/DC converter

2 交直流智能配电网系统数学模型

2.1 配电网CSC数学模型

交直流智能配电网系统中，通过CSC 实现配电网互联以及分布式交流电源的并网。根据基尔霍夫电压和电流定律，可以得到CSC 在三相静止坐标系下的电压电流关系表达式为

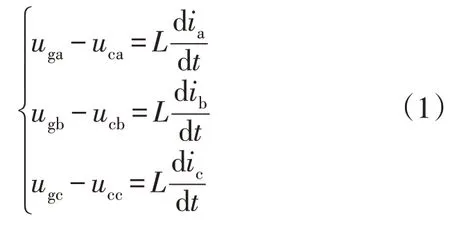
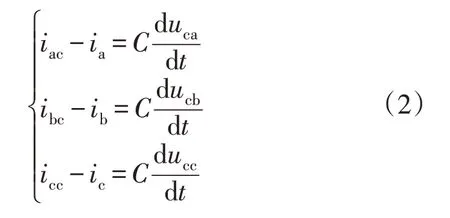
式中：uga、ugb、ugc为电网三相电压；ia、ib、ic为三相电网电流；uca、ucb、ucc为滤波电容电压；iac、ibc、icc为换流器交流侧电流。运用等功率变换，结合式（1）-（2），可以得到CSC 在两相旋转坐标系下的数学模型为

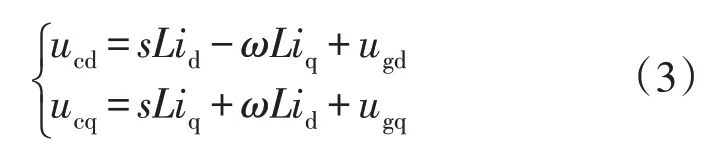
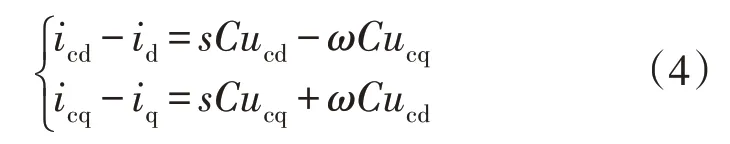
式中：ugd和ugq为电网电压的d、q轴分量；id和iq为电网电流的d、q轴分量；ucd和ucq为电容电压的d、q轴分量；icd和icq为CSC 交流输出电流的d、q轴分量。

CSC 正常工作时，上下桥臂均是有且仅有一个桥臂处于导通状态，采用SPWM 调制，CSC 交流侧电流可以表示为

式中：md和mq为ACC 调制度的d、q轴分量；Idc为CSC 直流侧电流。CSC 向配电网输出的有功功率和无功功率的表达式为

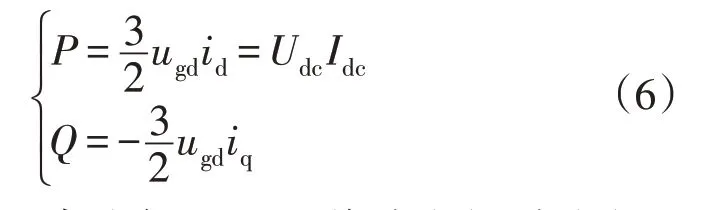
式中，Udc为CSC 直流侧电压。将式（3）、式（4）和式（6）代入式（5）可得到调制度与功率的表达式为

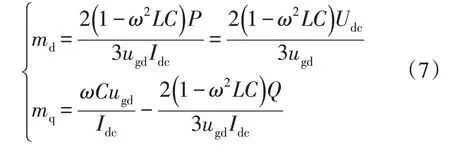
从式（7）中可以看出，通过改变调制度的d轴分量即可实现CSC 传输有功功率的调节，为了实现单位功率因数运行，调制度的q轴分量大小为

从式（8）中可以看出，若CSC 在功率变化过程中始终保持直流电流为额定值，则调制度的q轴分量基本维持不变。

2.2 基于CSC-VSC的混合DC/DC换流器数学模型

混合DC/DC 换流器并网侧采用CSC 拓扑，直流负荷侧采用VSC 拓扑，通过改变CSC 直流侧电压大小即可实现DC/DC 换流器功率调节。由于混合DC/DC 换流器的CSC 与配电网侧的CSC 结构完全相同，其数学模型不再赘述。在两相旋转坐标系下，混合DC/DC 换流器的VSC 的数学模型为

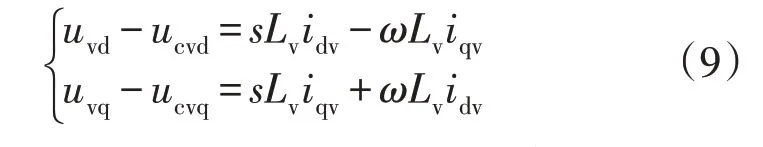
式中：uvd和uvq为DC/DC 换流器交流链路电压的d、q轴分量；idv和iqv为交流链路电流的d、q轴分量；ucvd和ucvq为VSC 交流侧电压的d、q轴分量。

混合DC/DC 换流器正常工作时，交流链路的电压和电流可以分别表示为

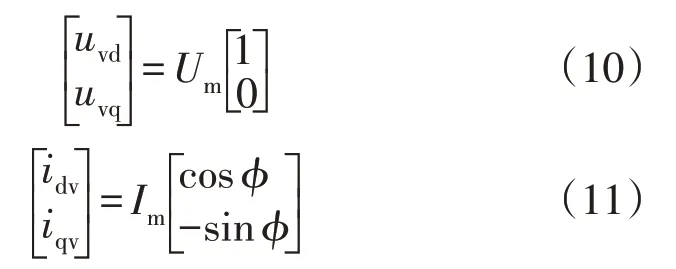
式中，Um和Im分别为交流链路电压幅值和电流幅值；f为电压电流之间的相角。

混合DC/DC 换流器的VSC 向直流负荷传输的有功功率和交流链路侧无功功率表示为

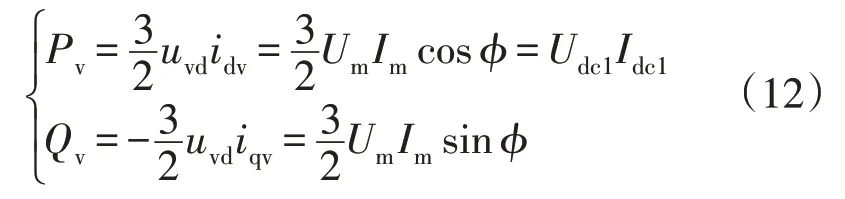
根据式（13），混合DC/DC 换流器单独控制VSC的d轴和q轴电流分量即可实现有功功率和无功功率的解耦控制。

3 交直流智能配电网系统控制策略

3.1 35 kV配电网侧CSC控制策略

根据前述分析，本文提出的35 kV 侧配电网CSC 采用定直流电流控制，控制框图见图5。

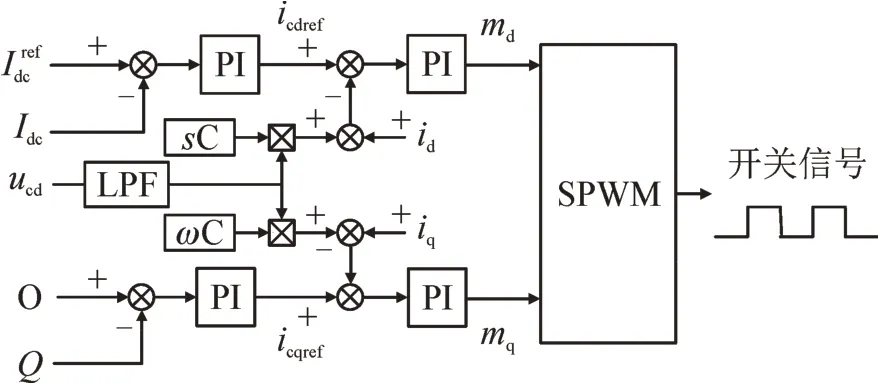
图5 35 kV配网侧CSC控制策略框图Fig.5 Control strategy block diagram of CSC at 35 kV distribution network side

直流电流通过PI 控制器输出后得到CSC 输出交流电流的d轴分量参考值，无功功率通过PI 控制器输出后得到CSC 输出交流电流的q轴分量参考值；结合CSC 的数学模型，CSC 输出交流电流参考值与计算实际值通过PI 控制器输出后得到调制度的d、q轴分量；采用SPWM 调制，得到CSC 的开关信号。由于35 kV 配电网侧CSC 采用多个CSC 换流器交流侧并联、直流侧串联结构，其中一个CSC采用图5 闭环控制，其余CSC 开环运行，其余CSC调制信号直接取图5 闭环控制输出的开关信号。

3.2 10 kV配电网侧和分布式电源侧CSC控制策略

根据前述分析，本文提出的10 kV 配电网侧和分布式电源侧CSC 采用有功功率和无功功率闭环控制，控制框图见图6。

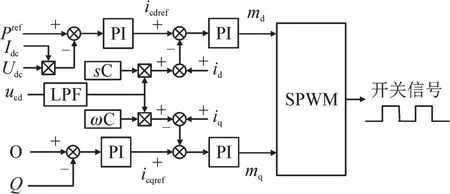
图6 10 kV配网侧CSC控制策略框图Fig.6 Control strategy block diagram of CSC at 10 kV distribution network side

有功功率通过PI 控制器输出后得到CSC 输出交流电流的d轴分量参考值，无功功率通过PI 控制器输出后得到CSC 输出交流电流的q轴分量参考值；结合CSC 的数学模型，CSC 输出交流电流参考值与计算实际值通过PI 控制器输出后得到调制度的d、q轴分量；采用SPWM 调制，得到CSC 的开关信号。

3.3 混合DC/DC换流器控制策略

本文提出的适用于混合DC/DC 换流器的控制策略框图见图7。

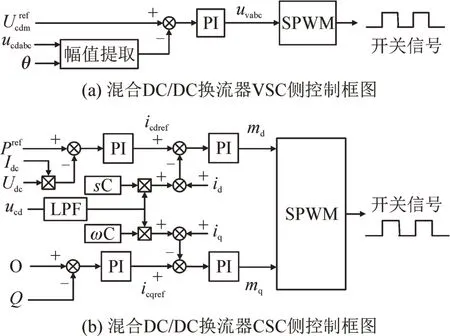
图7 混合DC/DC换流器控制策略框图Fig.7 Control strategy block diagram of hybrid DC/DC converter

通过采集混合DC/DC 换流器交流公共耦合点的三相电压，并在给定初始相位角的情况下求取公共耦合点的电压幅值，与电压参考值比较，电压差值经PI 调节器输出得到三相调制电压，从而得到混合DC/DC VSC 侧桥臂器件的开关信号。

通过采集混合DC/DC 换流器CSC 侧直流电压和直流电流得到换流器有功功率并与参考值比较后经PI 调节器输出得到调制度的d轴分量。通过采集交流侧电压电流得到公共耦合点处的无功功率，与参考值比较后经PI 调节器输出得到调制度的q轴分量。经过SPWM 调制，得到混合DC/DC CSC侧桥臂器件的开关信号。

4 仿真研究

为了验证本文提出系统及控制策略的正确性和有效性，在Matlab/Simulink 中搭建了图1 所示的仿真电路模型，电路参数见表1。

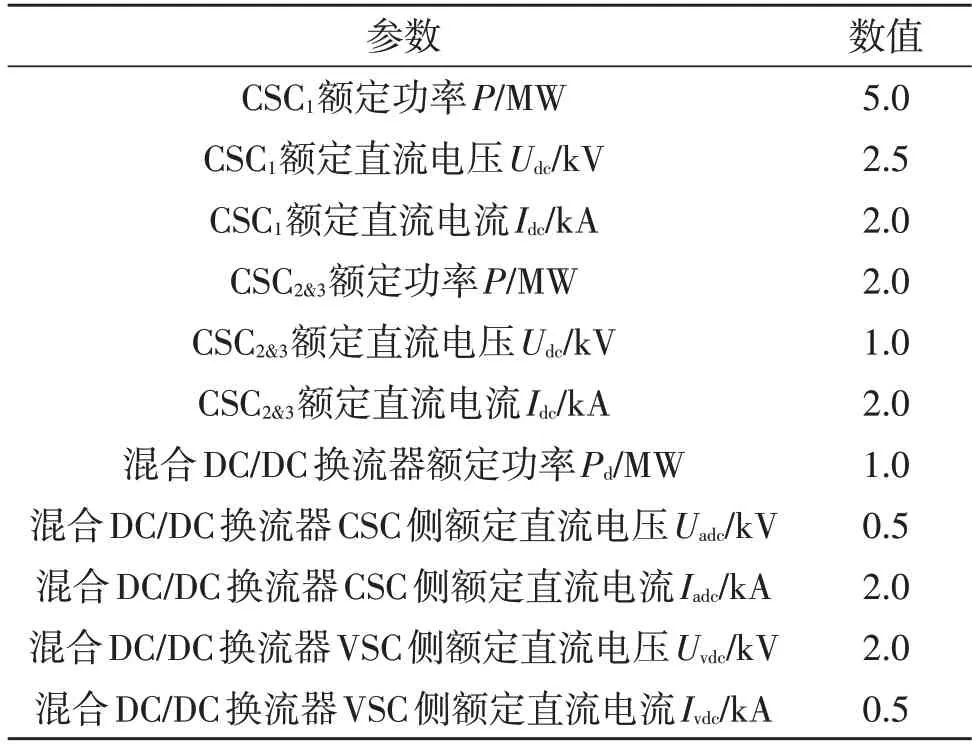
表1 交直流智能配电网系统运行参数Table 1 Operation parameters of AC-DC intelligent distribution network

1）算例1：系统稳态运行仿真。

系统处于稳定功率传输工况，仿真中设置35 kV配电网侧CSC1向直流电网侧输送3.0 MW 的有功功率，混合DC/DC 换流器向直流电网侧输送1.0 MW 的有功功率，10 kV 配电网侧CSC3和交流分布式电源侧CSC2分别从直流电网吸收2.0 MW 的有功功率，系统仿真结果见图8。

从图8（a）中可以看出，CSC1侧35 kV 配电网向直流电网输送了3.0 MW 的有功功率，混合DC/DC换流器侧分布式直流电源向直流电网输送了1.0 MW的有功功率，CSC2侧分布式交流负荷和CSC3侧直流电网分别从直流电网吸收了2.0 MW 的有功功率。

配电网系统直流电压水平如图8（b）所示。由于10 kV 配电网侧CSC3和分布式交流电源CSC2采用定直流电压控制，CSC2和CSC3侧直流电压稳定在额定值1.0 kV。仿真中，混合DC/DC 换流器VSC侧直流电压被认为处于额定值2.0 kV，由于混合DC/DC 换流器采用定功率控制，混合DC/DC 换流器CSC 侧即直流电网侧的直流电压在额定值0.5 kV附近。35 kV 配电网侧CSC1采用定直流电流控制，直流电压取决于其他换流器直流电网侧的电压和，即1.5 kV。

系统直流电流如图8（c）所示，系统直流电流稳定在额定值2 kA，混合DC/DC 换流器VSC 侧直流电流稳定在额定值0.5 kA。

CSC1、CSC2和CSC3交流侧电压电流波形分别如图8（d）和图8（e）所示，从图中可以看出，电压电流同相位，换流器均处于单位功率因数运行工况。

图8（f）所示为混合DC/DC 换流器交流链路电压波形。由于VSC 斩波的效果，交流电压波形含有大量的谐波分量，但基波幅值稳定在设计值0.8 kV。图8（g）所示为混合DC/DC 换流器交流链路有功功率和无功功率波形，从图中可以看出，交流链路处的无功功率为零，混合DC/DC 换流器处于单位功率因数运行工况。

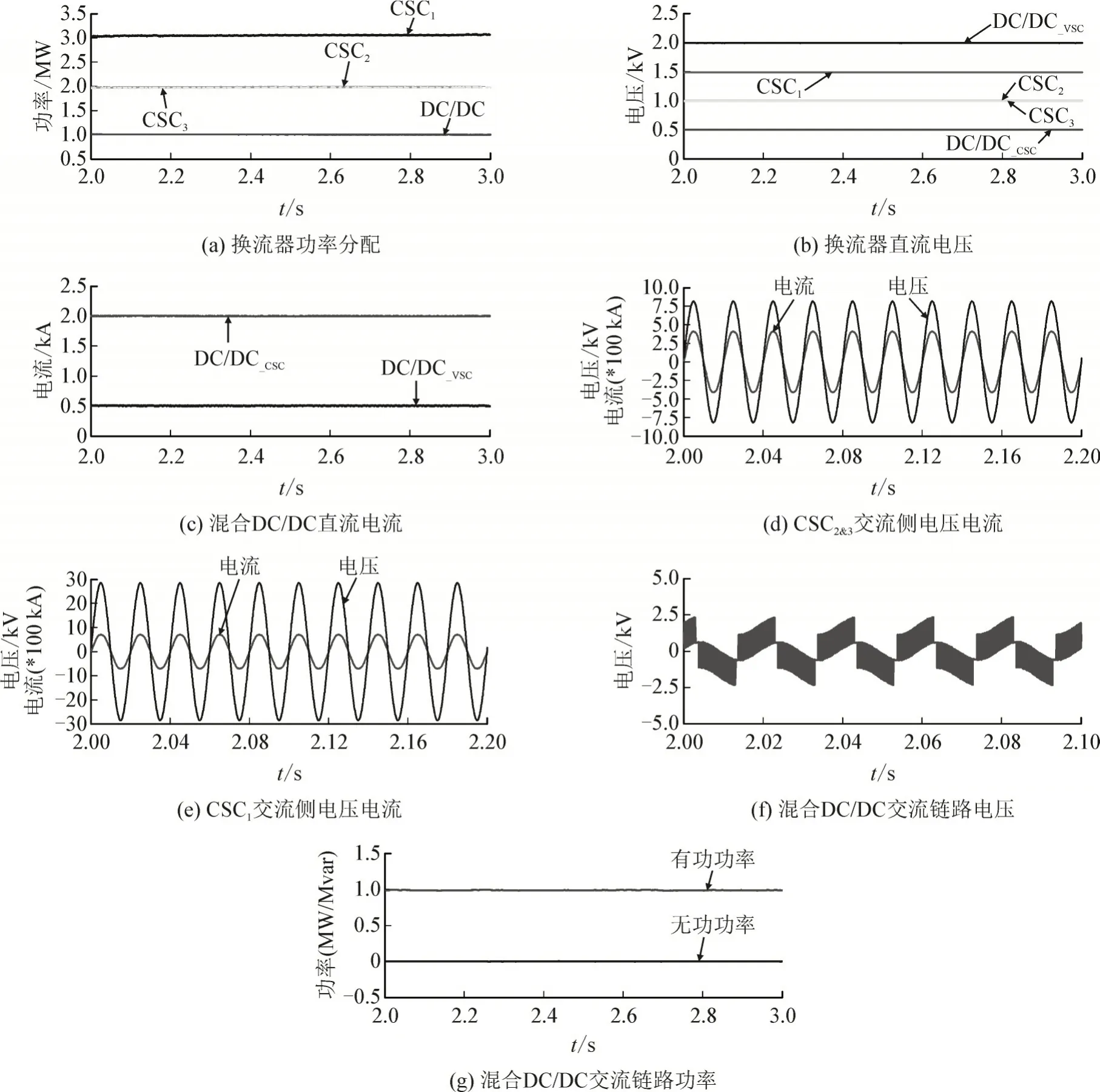
图8 系统稳态运行仿真结果Fig.8 Simulation results of steady operation of system

仿真结果验证了本文提出的网架结构和控制策略能够实现系统的功率稳定传输。

2）算例2：系统功率变化运行仿真。

仿真中设置系统5.0 s 前处于算例1 功率运行工况，5.0 s 时设置混合DC/DC 换流器向直流电网传输功率逐渐减小，而后变为从直流电网吸收功率且逐渐增大至1.0 MW，10 kV 配网侧CSC3和交流分布式电源侧CSC2传输功率保持不变，整个过程持续2.0 s，仿真结果见图9。

图9（a）所示为换流器的功率分配，从图中可以看出，CSC2和CSC3传输功率维持为2.0 MW。混合DC/DC 换流器向直流电网传输的有功功率由1.0 MW线性减小至-1.0 MW，CSC1向直流电网传输的有功功率由3.0 MW 线性增加到5.0 MW，功率变化过程平缓，没有任何冲击。

系统直流电压波形如图9（b）所示，从图中可以看出，混合DC/DC 换流器CSC 侧直流电压由0.5 kV 线性减小至-0.5 kV，VSC 侧直流电压维持在额定值2.0 kV，CSC2和CSC3侧直流电压稳定在额定值1.0 kV，CSC1侧直流电压由1.5 kV 平滑地增加至2.5 kV。

系统直流电流波形如图9（c）所示。由于CSC1采用直流电流闭环控制，在功率变化过程中，电网直流电流始终在额定值2.0 kA 附近，混合DC/DC 换流器VSC 侧直流电流由0.5 kA 线性减小至-0.5 kA。

由于CSC2和CSC3传输功率维持不变，故CSC2和CSC3仍然处于单位功率因数运行，CSC1交流侧电压电流波形如图9（d）所示，CSC1交流电流线性增大，在功率增加过程中，电压电流同相位，CSC1处于单位功率因数运行工况。

图9（f）和图9（g）分别是混合DC/DC 换流器交流链路电压和交流链路功率波形。从图中可以看出，交流电压幅值在功率变化过程中维持在额定值0.8 kV，混合DC/DC 交流链路无功功率始终为零。在功率变换过程中，混合DC/DC 换流器一直处于单位功率因数运行。

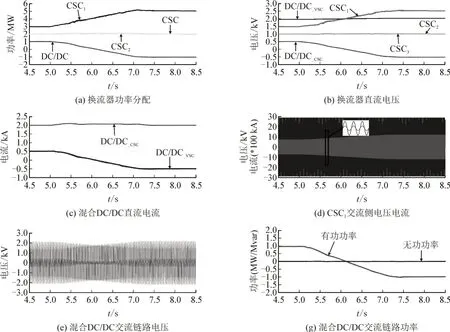
图9 系统功率变化运行仿真结果Fig.9 Operation simulation result of power variation of system

仿真结果表明了本文提出的配电网网架结构和控制策略能够实现系统传输功率的平滑切换。

5 结语

本文提出了一种基于电力电子柔性装置的交直流智能配电网网架结构，通过级联的CSC 拓扑实现35 kV 配电网的连接，通过CSC 实现10 kV 配电网和交流分布式能源的连接，通过提出的混合DC/DC 换流器拓扑实现直流分布式能源的并网。对智能配电网系统的数学模型进行了分析与研究，提出了适用于智能配电网系统的控制策略，实现了系统内所有换流器的单位功率因数运行。在Matlab/Simulink 仿真软件中搭建了仿真模型，仿真结果表明本文提出的控制策略能够实现系统稳定运行和功率切换。