基于多种群遗传算法和剩余矩形匹配算法不规则件优化排样

秦振浩

（河北工业大学经济管理学院， 天津 300400）

引言

二维不规则件排样问题是指将一系列形状不规则的二维平面零件尽可能以最优方式排放到矩形板材当中，使得板材的利用率最大。该问题广泛存在于现实的生产生活中，从钣金下料、玻璃切割、纸品剪裁再到家具生产，都能够看到其应用，在数学上该问题属于NP-Hard 的组合优化问题，计算过程复杂多变，计算量是呈爆炸性的，很难求出最优解。因此，对二维不规则件排样问题的研究具有重要的理论和实用价值。

本文通过矩形包络法将二维不规则件排样问题转化为矩形件排样问题，研究基于多种群遗传算法在零件入排序列和角度上的应用，以及剩余矩形匹配算法在零件排放策略中的应用，从而实现二维不规则件排样问题的综合求解。

1 问题描述及模型建立

二维不规则件排样问题通常可以描述为：将n 个形状不完全相同的二维不规则件{p1，p2，…，pn}不重叠地排放到m 张长为W、宽为H 的矩形板材A 中，在排样过程中，入排零件需要满足特定的条件才能保证排样过程顺利进行。这些约束条件包括：

1）pi与pj互不重叠；i≠j，i，j=1，2，…，n.

2）pi必须排在板材A 内部；i=1，2，…，n.

3）pi可以旋转一定的角度；i=1，2，…，n.

假设F 表示板材利用率，S 表示所有入排零件的面积之和，本文的研究目标为板材利用率最大，定义板材利用率为所有入排零件的面积之和与板材面积之比，则二维不规则件的数学模型如下：

其中：式（2）确保了入排零件之间没有交叠部分；式（3）确保了入排零件不超过板材的边界；式（4）中的表示零件旋转的角度，式（4）限制了零件可旋转的角度。

2 相关方法描述

2.1 不规则件的预处理

直接将不规则件排放到板材内部，操作起来相当复杂，需要考虑到复杂的几何问题，包括需要计算不规则件的大小、判断其排放位置和是否重叠等，为了简化不规则件的排样问题，学者们相继提出了一些零件预处理方法，包括矩形包络法、组合包络法等[1]。本研究组合使用这两种方法，对近似矩形的不规则件直接使用矩形包络法求其最小包络矩形，对形状互补的两个或多个零件首先进行平移、旋转进行组合包络，然后运用矩形包络法求其最小包络矩形，如图1 所示。

2.2 多种群遗传算法

零件的入排顺序问题属于典型的NP-Hard 组合优化问题，针对该问题，本研究采用多种群遗传算法，设置3 个进化种群，并将这3 个进化种群分为两部分，第一部分有1 个种群，该种群内的个体基因序列依据待排零件的面积有序生成，这是启发于现实中工人的经验排样，先排放面积大的零件再排放面积小的零件，这种排样方式能够起到加速收敛的目的，同时优先排放面积大的零件，面积小的零件在后续排样中将具有更高的灵活性[2]。第二部分有2 个种群，这2个种群内的个体序列都是随机生成的，设置2 个随机种群也是为了提高算法的搜索范围。

2.2.1 编码

本研究采用组合编码方式，用整数编码来确定零件的入排顺序，每个零件给定一个入排序号；用二进制编码来确定零件的入排角度，1 代表零件旋转90°，0 代表零件旋转0°，将零件入排序号排列成串再加上一个与之对应的二进制编码串就是一个可行解。

2.2.2 适应度函数

适应度函数是用来评价个体质量优劣的，个体的适应度值越高则质量越高，反之质量越低，文中采用的适应度函数为第2 节中的目标函数。

2.2.3 选择操作

本文基于轮盘赌法对个体进行选择操作，该方法以个体的适应度值为选择和淘汰的依据，个体的适应度值越大被选中的可能性越大，反之被淘汰的可能性越大。

2.2.4 交叉操作

为了提高算法的局部寻优性能，本研究采用自适应交叉概率pc，交叉概率的调整公式为：

式中：f1、favg和fmax分别表示要执行交叉操作的两个父代个体中较大的适应度值、种群内当前进化代数中父代个体的平均适应度值和种群内当前进化代数中父代个体中最大的适应度值；pc1和pc2为预先设定的两个固定值，从上式中可以看出个体的交叉概率pc会随着适应度值的取值情况动态地进行调整，为此可克服算法的不成熟收敛并避免优秀染色体被破坏[3]。判断两个父代个体是否交叉，通过在（0，1）内随机生成一个数r，当pc＞r 时，执行交叉操作，否则不执行。当染色体执行交叉操作时采用两点环形交叉方式[4]。

2.2.5 变异操作

与交叉操作相同，本研究同样基于自适应的思想，采用自适应的变异概率pm，变异概率的调整公式为：

式中：fm代表种群内待变异个体的适应度值；pm1和pm2为预先设定的两个固定值。对变异概率进行动态的调整既能保持种群内个体的多样化，还可以克服算法限入局部解的弊端。判断某个染色体是否变异，通过在（0，1）内随机生成一个数r，当pm＞r 时，执行变异操作，否则不执行。文中变异操作是对零件的入排顺序向量和入排角度向量进行的，对零件的入排顺序向量执行交换变异[3]，对入排角度向量执行旋转变异[4]。

2.2.6 移民操作

移民操作主要通过移民算子来进行，以使各个种群的进化不是相互独立的，而是相互影响、相互协调、协同进化的过程[5]。实施的原则是将每个种群中适应度值最低的个体用相邻种群中适应度值最高的个体进行替代。

2.3 剩余矩形匹配算法

在由多种群遗传算法产生个体编码后需要对其进行解码，本文采用目前提出的较为有效的排样定位方法- 剩余矩形匹配算法进行解码，该方法排样效果优于其他板材定位方法，可充分利用板材区域，使板材利用率达到最大，具体执行步骤如下：

1）初始剩余矩形集为整个板材；

2）按排样序列将零件排入到板材中，当排入零件时，先从最下方剩余矩形尝试排入，如果剩余矩形的长和宽均大于入排零件的长和宽则排入，排入时将零件放置到剩余矩形的左下方，更新剩余矩形集；如果待排零件不能排入到最下方剩余矩形的话，对其旋转90°再尝试进行排放，如能排入则更新入排零件的入排角度，更新剩余矩形集；如还不能排入，则尝试下一个剩余矩形，如果所有的剩余矩形都不能排入，则尝试排放下一个零件，更新零件的入排序列。

3）直到目前正在使用的板材已经拍不下任何零件后，则将剩余未入排的零件排放到下一张板材中，排放方法同第一张板材，直至所有零件全部排放到板材中。

3 实例验证与分析

为了验证本文算法的实用性和有效性，本文通过Matlab2018 进行编程实现，从A 公司收集了一些已经排样完的零件数据，对其进行预处理，采用预处理完的零件数据作为实验数据，所使用的原材料板材的规格为2 500 mm×1 250 mm。

本文算法的参数设置为：每个种群大小均为40、交叉概率和变异概率分别取[0.6，0.9]、[0.05，0.1]之间的动态值、最优个体最少保持代数为40 代，公司实际排样结果和本文算法所得排样结果见表1 所示。

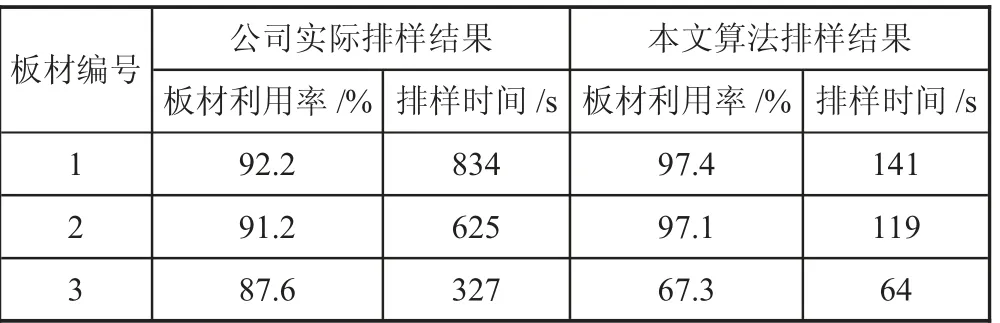
表1 排样结果对比

本文算法得到的第一张板材的排样图如图2所示。

从表1 中可以看出，排完所需零件公司和本文算法均需使用三张板材，但本文算法对原材料利用的更加充分，前两张板材的平均利用率高达97.25%，第三张板材的利用率仅为67.3%，要优于公司的排样结果。并且，本文算法的运行结果相对稳定，运行时间相对也较短，因此使用本文算法对板材进行优化排样可提高板材的利用率和排样效率，节省公司的生产成本。

4 结论

本研究以钣金件排样过程为应用背景，通过对不规则件进行预处理，求出不规则件的最小包络矩形，把不规则排样转化为矩形件正交排样，结合多种群遗传算法和剩余矩形匹配算法进行优化排样，找到问题的最优解，确定零件在板材上的合理排放位置。实例证明，本文算法能够提高板材的利用率和排样效率，降低企业的生产成本。