基于改进型能量控制策略的倒立摆系统控制研究

黄政杰，钟文键

（广东工业大学，广东广州 510006）

倒立摆的本质就是一个摆杆的支点（转轴）在这个摆杆的重心下方。倒立摆系统是一个非线性、多变量、强耦合、不稳定的系统。现实中有许多系统与倒立摆系统非常相似，如摄像机云台的控制，双足、四足机器人的稳定，空间飞行器和卫星的姿态控制等。从倒立摆系统衍生出来的科研成果极大推动了科技的发展，推动了航天科技、深度学习、机器人等领域的发展。

本文针对倒立摆的起摆和稳摆问题，设计一种将改进能量控制策略与模糊PID控制相结合的控制方法，使直线一级倒立摆系统能够实现平滑迅速的起摆和快速抗干扰的稳摆。本文所设计的控制方法通过了Simulink和Simcape MultiBody的仿真验证。

1 倒立摆系统建模

为了便于建立直线一级倒立摆系统的模型，首先假定系统内不存在任何摩擦力和阻力；各结构之间连接紧密，不会互相滑动。这样，直线一级倒立摆系统就可以等效成小车和摆杆所组成的系统，如图1所示。

图1 系统模型

为了方便后续计算，规定摆杆处于垂直向下的位置时，角度θ=-π；摆杆处于垂直向上的位置时，角度θ=0，角度范围为-π～π。定义为摆杆与垂直向下方向的夹角。

实际系统的模型参数见表1。

表1 系统参数

分析小车水平方向所受的合力，可以得到以下方程：

式中，N为由小车与摆杆相互作用力的水平方向的分量，F为小车的前进动力，为小车加速度，M为小车质量。对N进行分析，可以得到：

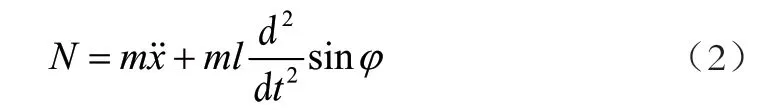
把式（2）代入式（1）中，得到系统的第一个运动方程：

然后对摆杆垂直方向上的合力进行分析，可以得到：

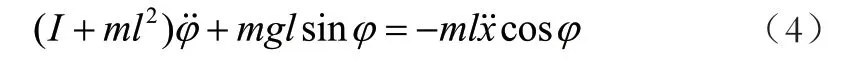
如果摆杆一开始是垂直向上的，控制倒立摆在外部扰动下保持垂直向上，不需要从垂直向下处起摆，那么 非常接近-π，则可以进行近似处理：cos=-1，sin=-经拉普拉斯变换后可得：

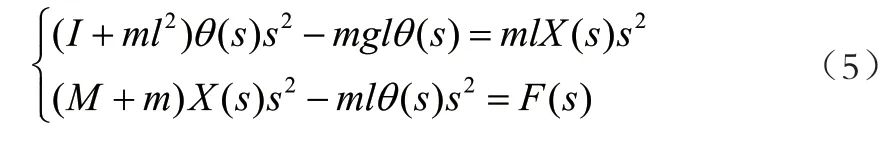
2 起摆算法设计

2.1 能量控制策略

若定义摆杆垂直向上时摆杆的能量为E=0，则摆杆于垂直向下位置（θ=-π）开始，运动到摆杆垂直向上的位置（θ=0），摆杆所需的能量为E=2mgl。设J为摆杆到轴的转动惯量，则J=I+ml2，结合式（4），可得：J+mglsinθ+mlcosθ=0。而摆杆的能量：

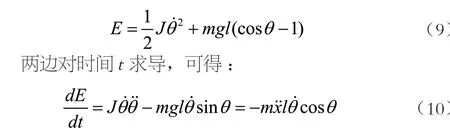
因为分析可知能量比角度更容易控制，且摇摆角θ在一四或者二三象限时小车会随着摆杆速度向上向下运动而左右运动，从而摆荡起来，起摆阶段完成。选择sign（cosθ）作为小车运动的方向，将摇摆角θ限制在一四象限，能量控制策略如式（11）所示：

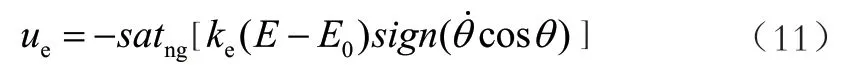
式中，ue为在误差e下的输出，satng为以ng为幅值的饱和函数；ke为比例系数；E为摆杆的能量；E0为目标能量，E0=0。

2.2 改进型能量控制策略

针对能量控制策略的缺点，本文采用改进后的能量控制策略。通过建立小车位置和速度惩罚算法，实现了有限长度的直线倒立摆的起摆控制。同时引入能量保持策略，捕获起摆后的摆杆，使其能维持在垂直向上附近的位置，这样便于后续的稳摆控制。

根据纯能量控制的缺点，将目标能量设为E0+μgl（μ＜1），以加快摆起速度，否则摆杆将近似处于一个无限接近的状态，如式（12）所示。

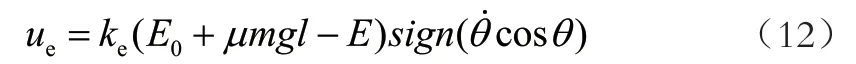
小车的位置惩罚，也就是当小车在导轨中间时位置惩罚为0，当小车在两边时惩罚非常大，迫使小车向导轨中间运动。这种惩罚可以用对数函数来实现，如式（13）所示，xmax为允许小车运动的最长距离，x为小车位置：

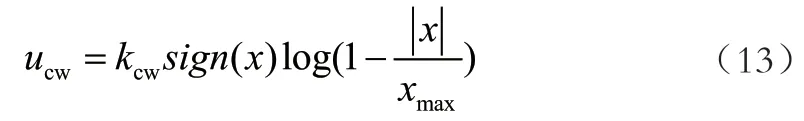
当摆杆摆到θ=0的位置附近时，摆杆经常是速度过大，因此引入能量保持策略，将摆杆的能量捕获在E=0的位置，如式（14）所示。

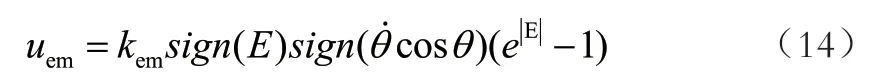
这样当摆杆角度误差较大时，能量保持策略的输出非常大，且显然uem与ue方向相同，此时uem与ue形成正向叠加关系，可以大幅缩短起摆前期用时。而如果摆杆角度在θ=0附近时，uem方向与ue方向相反，速度迅速降低，将摆杆的能量降低在E=0附近，使后面的稳摆控制更加平滑。

引入位置惩罚和能量保持策略之后，小车的速度常常过快，导致冲出导轨，因此需要引入速度惩罚，原理同位置惩罚。如式（15）所示：

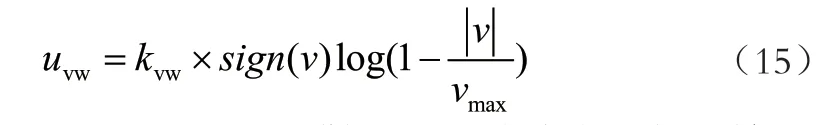
结合式（12）～（15），得到最终的改进型能量控制策略算法：

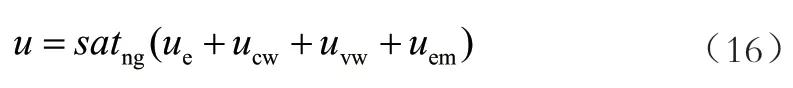
3 稳摆算法设计

本文引入模糊PID控制器，使用模糊控制器来时刻调整内环PID的参数，以求更好的控制效果，结构框图如图2所示。

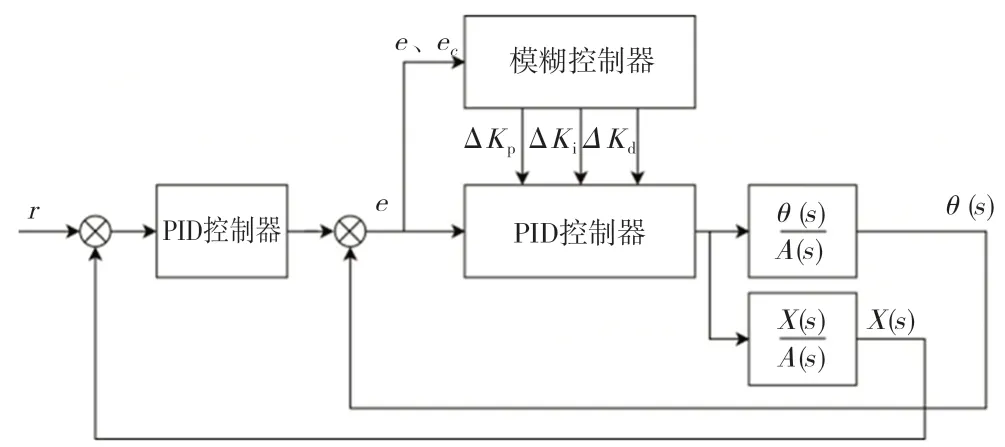
图2 倒立摆控制框图

本文选用Mamdani型模糊控制器，以误差e和误差的差分ec作为输入，以ΔKp、ΔKi、ΔKd作为输出，三者分别见表2～表4。量化因子Ke=2，Kec=0.1。解模糊化使用重心法，模糊控制器各个输入和输出的量化论域均选取为[-3，3]，选 取NB、NM、NS、ZE、PS、PM、PB作为输入输出空间的模糊分割。

表2 模糊规则表dKp

表4 模糊规则表dKd

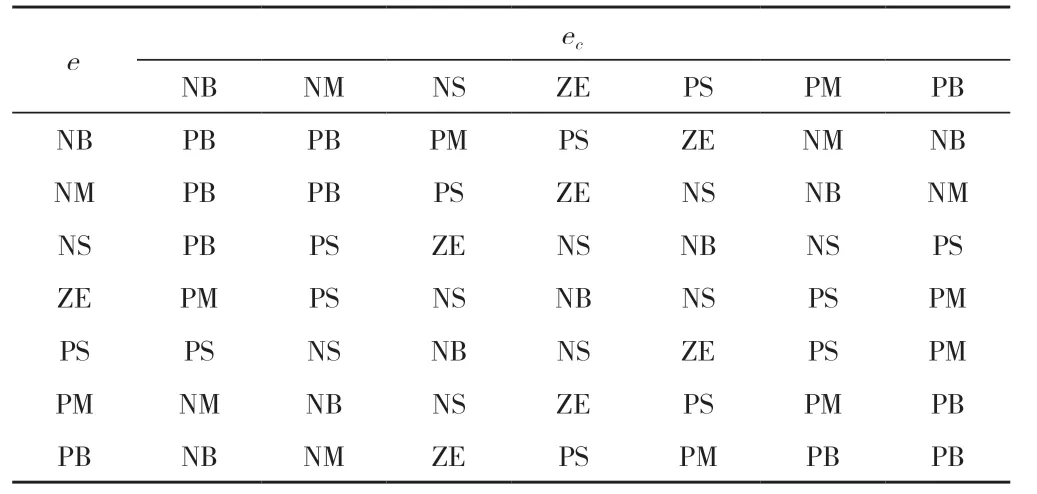
表3 模糊规则表dKi

3.1 模糊控制规则库设计

在本系统中，误差e较大时，应该适当增大Kp，以提高响应速度；在误差较小时，应该减小Kp，以减小超调量；而当误差非常小时，可以稍微增加Kp，以减少稳态误差，提升抗干扰能力。

在误差e较小时，可以增大Ki，以减小稳态误差；在e较大时，需要减小Ki。

对于Kd来说，在调节前期，需要增大Kd，以加快调节速度，减少超调量；在调节中期Kd不宜变化过大；在调节后期，应当减小Kd，避免振荡。

3.2 倒立摆3D仿真

MATLAB中的Simscape工具箱可以快速创建各种系统模型，在生成这些模型的同时与Simulink中其他组件直接连接。本文使用Simscape MultiBody组件建立一个3D倒立摆模型，并用于算法验证。

首先使用Simscape MultiBody建立一个机械仿真环境，并设置重力加速度为-9.80665m/s2。然后建立3个长方体块，分别作为导轨、小车和摆杆，并分别设置好对应的长宽高和质量。其中小车通过一个滑块连接到导轨的顶面上，而摆杆通过一个旋转节点与小车相连，如图3所示。

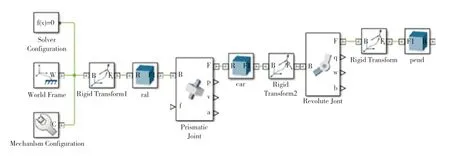
图3 倒立摆3D模型

随后将其封装为一个子系统，并在Simulink中调用。为了对比，首先使用传统的串级PID控制，令比例因子kkp=kki=kkd=0，Kp=140，Ki=100，Kd=44，运行结果如图4和图5所示。

图4 倒立摆3D仿真

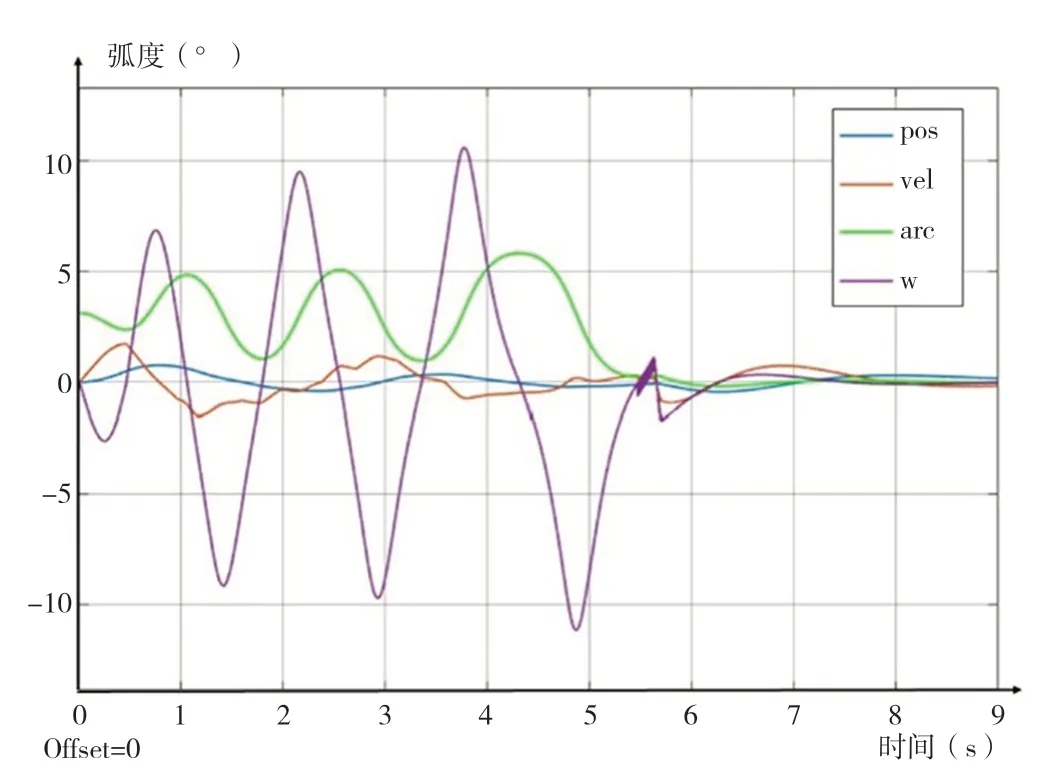
图5 起摆+串级PID控制效果

从图4中可以看到，起摆阶段中，摆杆迅速平滑地荡起，当摆杆接近垂直向上的位置时，其角速度也接近0，同时小车位置也不会偏离原点太多。

稳摆阶段中，串级PID控制的切换不够平滑，而且调节时间较长。并且经过多次实验，切换平滑和调节时间难以兼得。

令比例因子kkp=10，kki=20，kkd=20，Kp=80，Ki=25，Kd=50，仿真结果如图6所示。

图6 起摆+模糊PID+串级控制效果

显然，内环PID控制器改用模糊PID控制器之后，不仅切换变得更加平滑，而且调节时间也有了大幅改善。

4 总结

本文采用改进型能量控制策略，相比于能量控制策略，改进型能量控制策略不仅能够加快起摆速度，还实现了可限制小车位移和速度的起摆控制。

稳摆阶段中，本文在串级PID控制的基础上，将内环控制器改为模糊PID控制器，并成功与改进能量控制策略较好地结合起来，实现了更加平滑的切换、更加迅速的调节、更小的超调，同时也具有串级PID的优点：小车位置可控，抗干扰能力强。