基于ArcGIS Engine的水深点与等深线检查方法及实现

杨广武

（广东省国土资源测绘院，广东 广州 510663）

0 引 言

水深点、等深线是水下地形测量的主要组成部分，能直接地表示水下地形的起伏状态及反映水底地貌。等深线在生产过程中以软件程序初步生成，再进行人工修改，在人工修改部分就难免会出现部分水深点与等深线水深值不一致或者丢失等深线的现象。传统人工的逐点排查水深点与等深线矛盾不仅增加了内业人员的工作量，还容易导致检查不完整出现错漏，甚至产生新的错误，尤其在大批量的数据下，这种人工目视检查水深点与等深线矛盾的方法不但检查效率低下，而且对数据的正确性也难以控制。本文提出将大范围的水深点和等深线进行分区，再利用水深点构建不规则三角网（Triangular Irregular Network,TIN），将TIN 边线与等深线相交比对算法来判断点线矛盾，既能准确的找出点线矛盾和丢失等深线问题，又能更加快速查出错误，并且以.NET 为平台，结合ArcGIS Engine 组件，以Microsoft Visual Studio 2010 为开发环境，Visual C#为系统开发语言实现该算法。

1 算法原理与方法

1.1 数据分区

目前有关等高线点线矛盾的检查方法，已有不少学者提出了算法，比如不规则三角网（TIN）检查法、放射线检查法等。这些算法基本实现高程点与等高线矛盾的检查，但是存在一些缺陷：不规则三角网检查法，结果的准确率较高，但程序运行速度较慢；放射检查法虽然程序运行效率高，编程简单，但是检查结果的错误类型单一，疑似错误率相对较高。本文采用了不规则三角网（TIN）检查法检查水深点与等深线矛盾问题，但为了程序运行效率，增加了先将水深点与等深线进行分区循环再检查的思路，即大大提高检查的速度且不影响检查结果。

数据要分区，其实还有数据本身原因，本文程序成果主要用于1：10 000 比例尺水下地形测量水深点与等深线数据库检查。在1:10 000 比例尺的水下地形图中水深点测量时，设计的航线要求是相互之间隔100 米，航线上的测量水深点相差50 米。在相同陆地比例尺、面积内的高程点数量会远低于水深点数量，导致程序运行起来更加缓慢。等深线直接采用0、2、5、10、15、20、25、30、35、40、50 米（之后以10 米作为等深距）作为等深值，虽然等深线与等高线数量相比要减少很多，但由于海底地形普遍平坦和等深线之间距离较大，等深线横跨距离相当长，且海域范围普遍较大，都会降低程序运行速度，甚至程序直接崩溃。采用水深点与等深线分区再循环检查，这问题就轻松解决了。

数据分区算法原理：首先将水深点与等深线遍历获得检查全区域的范围坐标，其次按照固定的长度、宽度进行分区，由于在1:10 000 比例尺中水深点之间距离保持在100 米左右，因此相邻分区需要重叠150 米左右来解决分区之间遗漏构建TIN 的问题。

1.2 构建TIN

现存关于构建TIN 的方法已经很多，在二维约束Delaunay 三角网（Cormtrained Delaunay Triangular Irregular Network,CD-TIN）构建的方法，首先对约束数据集建立非约束Delaunay 三角网，其次将约束线段嵌入应用，学者刘学军等提出约束线段嵌入迭代算法和学者刘少华对其进行了改进和补充。本文构建TIN 过程采用生长三角形法，由于只用于点线矛盾的检查，未进行最小角最大优化，该方法简单、易于编程实现。在提高程序运行效率和程序简洁，还将构建TIN 工作放置到后台运行。为了防止冗余计算，将TIN 简化为离散边，即将TIN 的各边全部使用单一线连接，两个点之间只保留一条线，不重复连线。

1.3 点线矛盾分析

水深点与等深线矛盾检查的前提是假设每个水深点的水深值都正确，再来检查等深线的水深值正确性及是否遗漏等深线，是等深线重新生成的过程。在利用水深点构建TIN，用TIN 边线与等深线相交，且记录等深线水深值，其次利用该TIN 边线两端的水深点的水深值分析得到穿过该边线的等深线水深值。为数值，为数组，与之间判断逻辑关系为：（1）包含，则合理，从中移除。（2）不包含，则为多余的等深线值。（3）该边线与所有等深线相交后，中还存在数值，则为遗漏的等深线值。

图1为存在多余等深线空间位置关系图，会记录边线AB 之间多余2 米等深线。

图1 多余等深线关系图

图2为遗漏等深线空间位置关系图，会记录边线AB 之间遗漏15 米等深线。

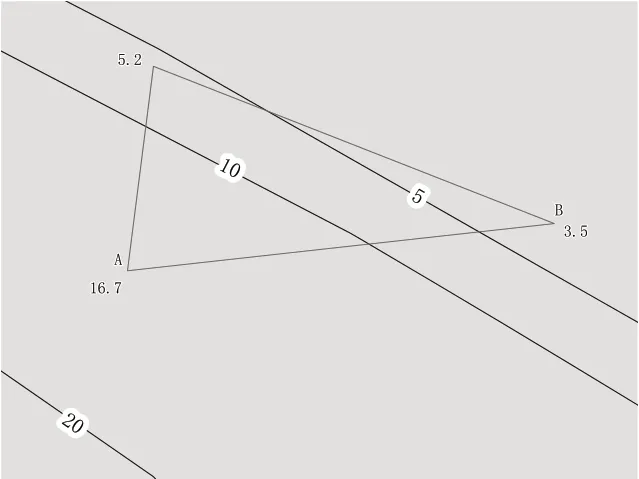
图2 遗漏等深线关系图

2 程序实现步骤

2.1 ArcGIS Engine 简介

ArcGIS Engine 是美国ESRI 公司基于ArcObjects 的推出的独立工具包，主要用于开发C/S 应用系统，它是将ArcObjects 的部分功能进行封装构建组件库，软件开发人员可以调用任何支持COM 的编程语言进行编程，如C#、Visual Basic.NET、Visual Basic、Java、C 语言、C++ 语言等，在不同的操作系统平台和软件开发环境安装相对应的ArcObjects SDK，便可以让开发者能够快速且方便的开发出自定义的GIS 应用程序。用户需要安装ArcGIS Desktop 才能保证应用程序正常运行。开发所具有的特点包括：继承性、专业性、复杂性、实用性、紧迫性等。

2.2 程序设计示意图

本文在假定水深点值是正确的前提下，首先将水深点和等深线分区，其次将分区的水深点构建TIN，遍历TIN 边线，通过比较两端点之间的水深值及分析TIN 边线与等深线的交点，按照1.3 中所述的逻辑关系进行判断可以准确地知道水深点与等深线之间的矛盾是否存在，具体算法流程如图3所示。

图3 程序设计示意图

2.3 关键代码

2.3.1 数据读取

选择数据存储的数据库，筛选出数据库水深点和等深线图层，依次对每个水深点和等深线进行遍历，核心代码为：

2.3.2 数据分区

各分区范围的Min_X、Max_X、Min_Y、Max_Y 值，遍历水深点将水深点分区，遍历等深线进行分割得到各分区等深线。部分核心代码如下：

2.3.3 数据判断

利用各分区后的水深点和等深线，再遍历各分区水深点和等深线进行检查，首先将水深点构建TIN，提取TIN 边线且记录两端点的水深值，其次遍历TIN 边线时剔除长度大于300 米的边线，可以减少误报和程序运行速度，再判断TIN边线与等深线交点数量和两端点水深值判之间存在的等深线数量，最后根据点线矛盾关系得到检查结果。部分核心代码为：

3 应用实例分析

为了充分验证算法程序的实际应用效果，本文选取湛江市湛江港附近海域1:10 000 水下地形图数据进行实验性检查，该海域航道较多，地形复杂，最大水深达40 米，共有31 206 个水深点和368 条等深线。现将水深点与等深线数据分成三个区域进行实验，人工检测和程序检测进行比较的结果如表1所示。

表1 程序和人工检测结果对比

通过实验结果分析表明：数据检查的时间跟水深点和等深线的数量有关系，水深点越多数据检查使用的时间越长；同理，等深线越多，数据检查所使用的时间也越长。数据的数量与时间基本成一种线性正比关系。

程序检查的错误100%包含了人工检查出来的错误，同时还检查出人工遗漏的错误。通过对实验数据结果分析，人工目视方式检查水深点与等深线矛盾的遗漏率达到15%左右。在数据检查所需的时间上，程序检查所需时间大大低于了人工检查所需时间。因此本实验表明，该水深点与等深线矛盾检查方法在实际工作中具有很高的应用价值。

在生产工作实际中，作业员只需对水深点与等深线矛盾检查结果进行排查和修改，便可以大大缩短解决点线矛盾问题的时间。

4 结 论

本文对不规则三角网检查法在编程实现运行慢的问题上提出了数据分区解决法，并在ArcGIS Engine 平台下实现了对mdb、gdb 数据进行的水深点、等深线线矛盾检测。从理论上和实际上都达到了预期，可以明显减轻质量检查人员在检查水下地形图的水深点与等深线矛盾错误时的工作强度，并且在提高整体工作效率和数据质量正确率中发挥了重要作用。解决了质检人员人工查找水深点与等深线矛盾的难题，在实际工作中具有很好的应用价值。