面向目标识别的特征聚类与选择方法研究
桂洪冠,位凯
(1.达而观信息科技(上海)有限公司,上海 201203;2.上海海事大学,上海 200135)
0 引 言
目标识别在智能驾驶、智慧交通、智慧安防等多个领域有广泛的应用,是实现系统智能决策的重要基础。为了进一步准确地识别目标,需要使用标注数据预先训练一个分类模型。在识别模型训练过程中,需要对大量的识别目标进行特征选择,所选特征的数量及其重要程度直接影响到分类准确率,进而影响目标识别的识别效果。现有的特征聚类算法以联合非负矩阵分解(Joint Nonnegative Matrix Factorization,JNMF)为主,该算法对噪声较为敏感。联合稀疏典型相关分析(Joint Sparse Canonical Correlation Analysis,JSCCA)是一种具有代表性的特征选择算法,但JSCCA 及其改进算法大多为无监督方法,无法在不同组别之间同时执行并寻找组别之间的特征差异。
本文提出一种未知目标与已有知识图谱中的目标之间的高效特征关联与选择的方法,旨在提高目标识别模型的分类准确率。首先基于JCB-SNMF(Joint Connectivity-based Sparse Nonnegative Matrix Factorization,JCB-SNMF)模型将两个数据集中的显著特征聚类,再将选出的特征放入MTSCCALR(Multi Task-Sparse Canonical Correlation Analysis Linear Regression,MT-SCCALR)模型进行特征关联分析。在模拟数据集的实验表明,该方法可以有效解决目标识别领域训练数据集特征冗余以及分类准确率低下的技术问题。
1 现状
现有的特征聚类算法以联合非负矩阵分解(Joint Nonnegative Matrix Factorization,JNMF)为主,JNMF 算法通过将不同模态数据的矩阵进行拼接,然后再进行分解来达到降维的目的。降维后得到的基矩阵存放样本信息,系数矩阵存放特征信息。对于特征共表达模块的选择,一般对系数矩阵的每一行采用z-score 标准化后与人为设定的阈值进行比较,当标准值大于阈值,则认为该特征有资格进入到该模块。在JNMF 基础上,将先验知识加入能够有效提高模型的特征关联分析性能。但是,大多数改进算法对数据中存在的噪声较为敏感,在噪声较大的情况下无法正确选择重要特征。联合稀疏典型相关分析(Joint Sparse Canonical Correlation Analysis,JSCCA)是一种具有代表性的特征选择算法。JSCCA 通过得到两种数据特征之间最大相关性的线性组合挖掘更显著的特征。在JSCCA 基础上,也可加入各种先验知识以增强数据之间的相关性。但是JSCCA 及其改进算法大多为无监督方法,无法在不同组别之间同时执行并寻找组别之间的特征差异。
当前技术的特征关联分析与选择方法还存在准确率和召回率不高的问题,尚无法达到实际应用的需要。如何高效利用已有的知识图谱中的目标数据集信息进行有效的特征聚类与选择,进而训练出准确率高、召回率高的识别模型,目前尚未提出有效的技术方案。
2 方法
本文提出的面向目标识别的知识图谱辅助特征聚类与选择方法包括两部分,第一部分提出一种JCB-SNMF 的特征聚类方法,该方法能够将目标识别的训练数据集和对应的知识图谱中的目标特征投影到同一个公共特征空间,通过这种方法可以实现将显著特征聚类到显著共表达模块。第二部分提出一种MT-SCCALR 的特征关联与选择方法,该方法能够将第一部分筛选出的训练数据集和目标数据集显著特征进行关联分析,进而按需求选出其中的Top 特征用于后续分类。方法过程如图1所示。

图1 特征聚类与选择过程
2.1 特征聚类方法
2.1.1 特征预处理
训练数据样本集指在目标识别之前预先训练的已有标注的样本,根据标注信息,可在知识图谱中找到与其对应的目标类型和全部特征信息。根据训练数据的标注信息对训练数据按标注类型排序,对应于训练数据的特征(如飞行目标的速度、高度、航向角等),形成一个每行为一个样本,每一列为一个样本特征的数值矩阵。
2.1.2 JCB-SNMF 特征聚类算法
JCB-SNMF 算法是在JSNMF(JointSparseNonnegative Matrix Factorization,JSNMF)算法的基础上进行的改进。具体为:
NMF 是传统的降维方法,其一般模型为:
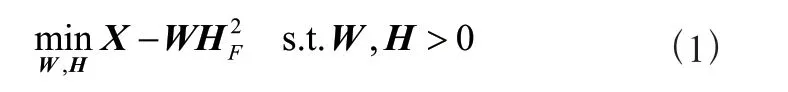
其中,和分别是原始特征矩阵经分解得到的基矩阵和系数矩阵,且的维度是行列,的维度是行列,的维度是行列。、和分别代表样本数、特征数和降维数。JNMF 算法在NMF 算法的基础上扩展了输入数据的种类,即可对多个不同模态数据的特征矩阵同时进行分解,其目标函数为:
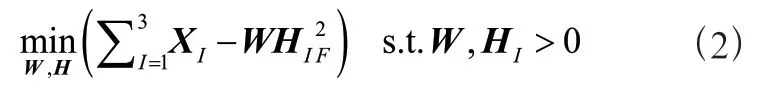
X∈R(=1,2,…)代表不同数据的特征矩阵,行数相同,列数不同。∈R代表分解后的公共基矩阵。H∈R代表分解后的对应于原始矩阵的多个具有很强独立性的系数矩阵,实际使用中<<,有学者提出了JSNMNMF,文中为了改善数据之间关联较弱,假设为相互作用邻接矩阵,JSMNMNMF 采用了范数和范数分别控制和H的稀疏性以实现数据的稀疏化。因此,其目标函数为:
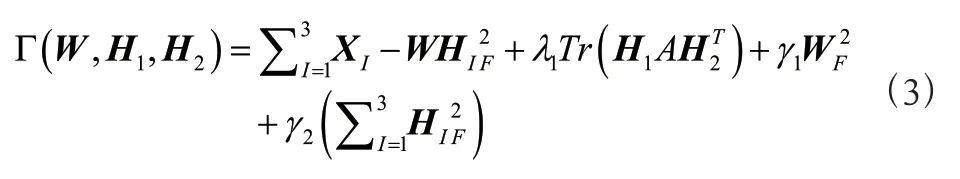
、、分别代表邻接矩阵的权重,用于控制的稀疏度,用于控制H的稀疏度。
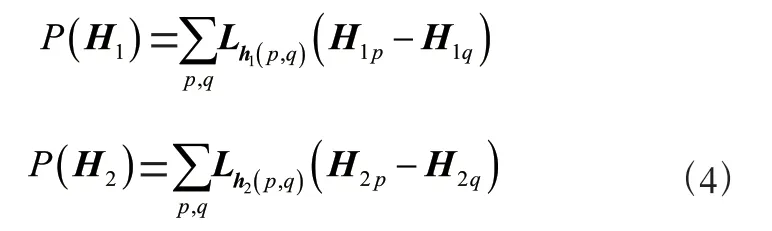
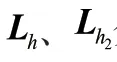
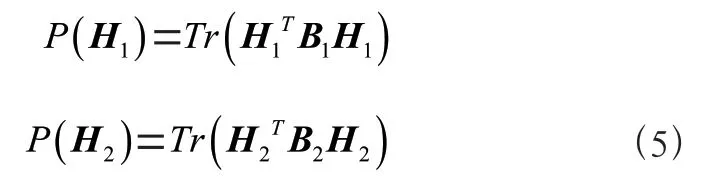
、分别代表、的拉普拉斯矩阵。给出所提出算法的目标函数为:
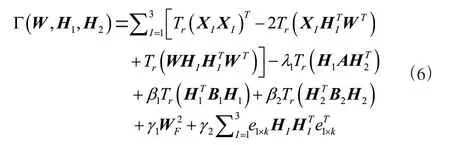
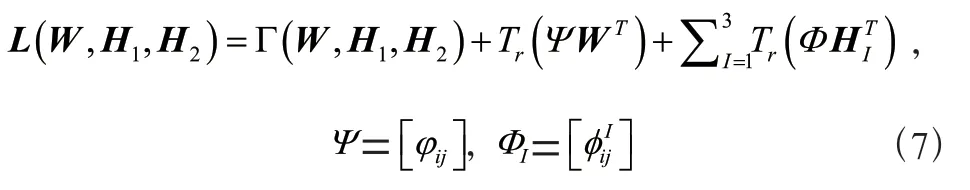
关于和H的偏导为:
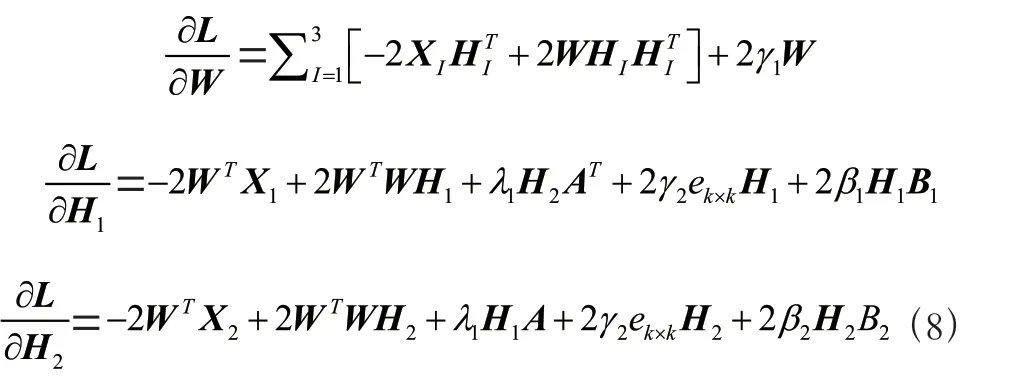
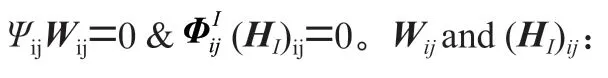
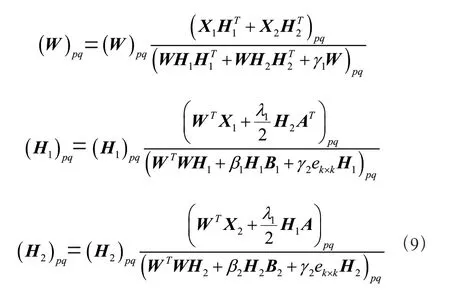
根据式(9)的迭代规则,最终将和分解成基矩阵和系数矩阵、。为了找到的每一行的显著特征对应的权重值,使用z-score 来提取H矩阵每一行的系数。它的定义为:

其中h代表H中的元素,μ代表中H特征的平均值,σ代表标准差。为了确定模块成员资格,须人为设置一个阈值,如果它的z-score 值比给定的阈值大,则有资格分配到模块。
接下来,评估每个模块的显著性。具体来说,假设A=[,,…,]、B=[,,…,]。其中,a、b分别是从、中选出的列向量。然后,使用式(9)计算同一模块中元素的平均关联性。

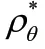
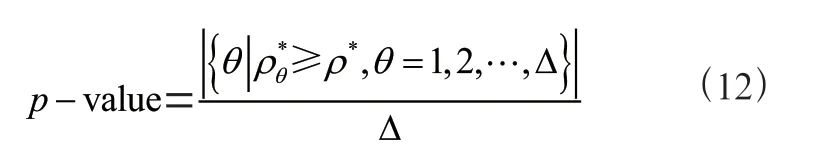
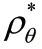
在本专利中,、分别代表训练数据和知识图谱中对应的目标样本集,根据实际样本数量和特征数量确定模块数,一般<<。通过式(8)随机初始化、、,通过多次迭代,使其收敛到一个局部最小值。进而得到公共基矩阵,以及分别对应于、的系数矩阵、。然后根据式(9)计算同一模块中元素的平均关联性。最后根据式(10)、式(11)对所有模块进行显著性分析,筛选得到最显著的模块,模块中包含两个数据集的显著特征用于后续分析。
2.2 知识图谱辅助特征关联分析方法
将2.1 章节所述的不在模块中的特征剔除,保留两个矩阵在模块中的特征。将训练数据标签和两个矩阵拼接放入MT-SCCALR 模型,该模型同时执行多个不同类型目标的任务,对于每种目标类型都会求出其每个特征的权重向量,对取绝对值后,按权重从大到小排列。根据需要取每一种目标的Top 特征用于后续分类器分类。具体有以下4 个步骤:
(1)将训练数据样本集和与其对应的知识图谱中的目标样本集一一对应。其中,根据训练数据样本集标注的信息,可在知识图谱中找到与其对应的目标类型和全部特征信息。进而,分别得到训练样本集和知识图谱的特征矩阵(行为样本,列为特征),其行数相同,列数不同。两个矩阵中样本应是一一对应的。
(2)使用JCB-SNMF 模型将两个数据集中的显著特征聚类。
(3)将选出特征放入MT-SCCALR 模型进行特征关联分析。MT-SCCALR 模型是在传统的基于SCCA的无监督方法基础上实现的改进。
CCA算法是一种确定两个数据集之间关联的算法。给定数据集∈R和∈R,其中有个特征,有个特征,共个样本。该算法能够找到和最大相关性的线性组合。
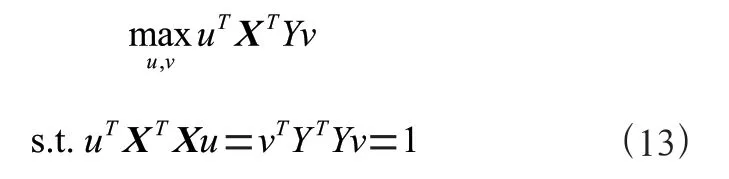
其中,假定和的列已经标准化,和是和对应的标准化后的特征权重。
SCCA 模型是在CCA 的基础上加入了惩罚项,用于控制模型的稀疏性,SCCA 模型定义为:
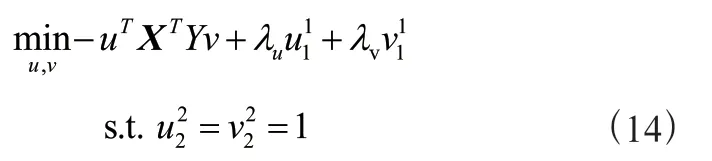
MT-SCCA是一种新颖的模型,它在SCCA 上加入了多任务框架。创新性的在其基础上加入线性回归模型,这使得不同目标的类型标签可以加入。使用来表示目标的种类。分别使用∈R和∈R表示经JCB-SNMF 算法筛选得到的训练数据集中的目标特征和对应的知识图谱中的目标特征。∈R是X的权重矩阵,∈R是Y的权重矩阵。
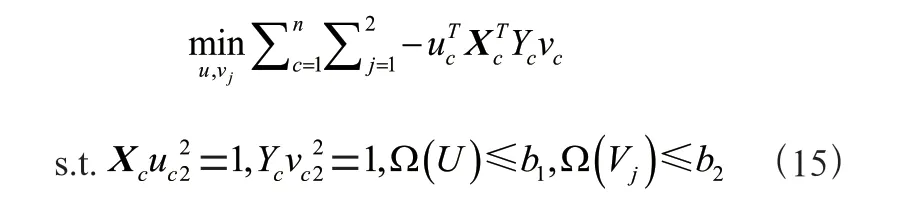
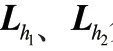
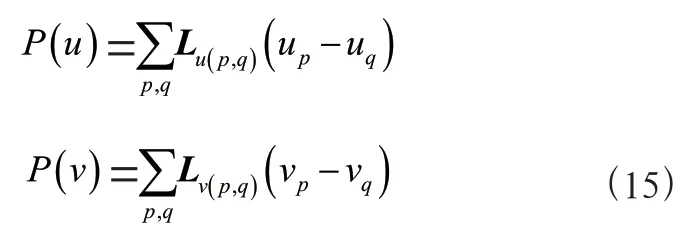
其中,L和L分别代表和的拉普拉斯矩阵,可将其改写为:
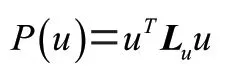

然后在模型中引入线性回归,其目标函数为:
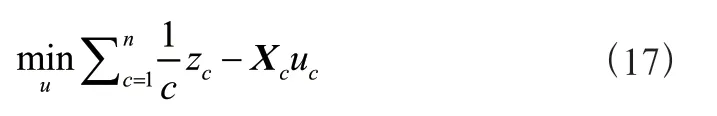
z代表第个任务的第个标签。现在可以给出加入线性回归的模型的目标函数:
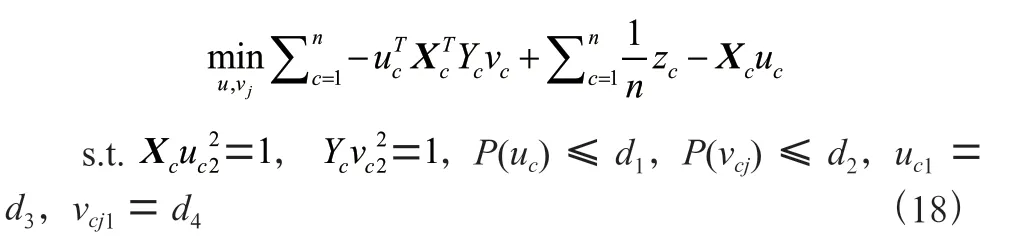
然后,得到MT-SCCALR 算法的目标函数,如式(19)所示:
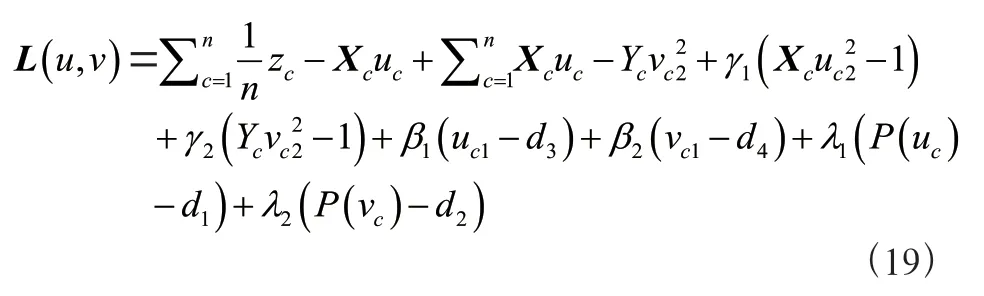
其中,、、、、以及是需要调整的超参数,、、和用于控制模型的稀疏度。删除常量后,得到式(20):
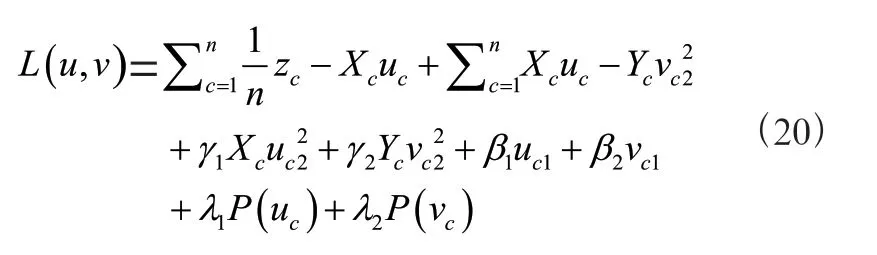
为了最小化目标函数(20)以获得最优的和算法,使用交替凸搜索方法。首先,初始化和,然后,当固定时,修改,反之亦然。并重复上述过程直至收敛。
首先得到一个的值,当是常数时它被最小化。由于拉普拉斯矩阵是正定矩阵,基于连通性的惩罚是凸的,可以使用基于软阈值的坐标进行优化,因此(20)的坐标解定义为:
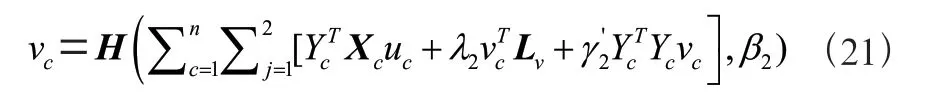
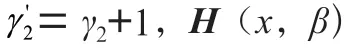
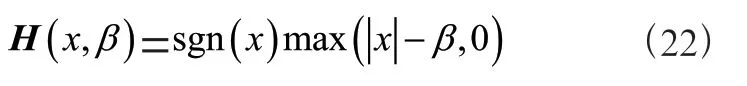
在得到之后,开始对求偏导,的目标函数如式(22):
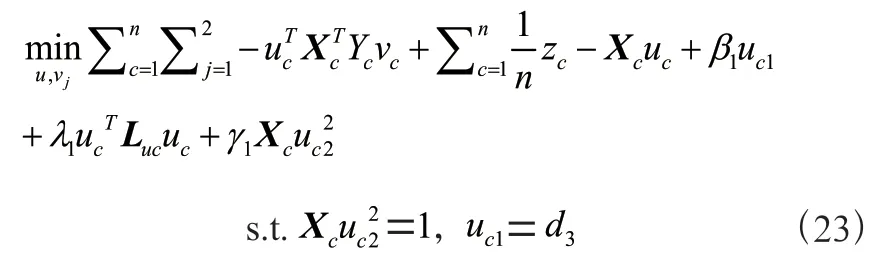
用这种方式,可以迭代得到权重的值,如式(24):

(4)得到训练样本集各特征权重,取绝对值后按需要保留Top 特征。将步骤(3)中得到的权重向量u拼接,得到权重矩阵,对取绝对值,其中中列中的每个元素对应于矩阵的每个特征。将每一列从大到小排序。然后根据需要找到Top 特征,用于后续分类等。
3 实验分析
3.1 数据集预处理
对于原始训练数据集,需要经范数归一化,目的在于:
统一数据单位:可以将有单位的数据转为无单位的标准数据,在目标识别场景下,训练数据集和知识图谱中已有目标的各种参数可能使用了不同单位,将这些数据经过归一化统一都映射到(0,1)这个区间,这样能够保证所有数据的取值范围都在同一个区间里的。
此外,归一化可有效避免模型梯度求导计算时在垂直等高线的方向上走大量无畏的之字形路线,从而减小迭代计算量和迭代次数,加快模型收敛速度。
对应知识图谱中的数据集,在知识图谱中依据训练数据标签找出对应的目标全部特征,然后同样进行范数归一化处理。得到与训练样本集行数(样本)相同、列数(样本特征)不同的数值矩阵。
3.2 模型参数选取
将预处理好的训练样本数值矩阵和与其对应的知识图谱中的数据放入JCB-SNMF 模型中,调整模型参数、、、、。对于模块数的选取,需要固定其他参数,然后将逐渐增大,在保证<<的情况下,比较不同值下的目标函数值,选取目标函数值最小的作为模块数。此外,固定以上参数后,随机初始化100 组、、的参数组合后,计算100 组参数组合下的目标函数值,选取最小的目标函数值对应的参数组合。最后利用式(8)迭代更新使得模型收敛到局部最小值。
3.3 特征聚类
根据式(10)(11)可以计算出个共表达模块的显著性值,选取最显著的模块(<0.01)。提取最显著的共表达模块中包含的特征,更新矩阵和,使用该模块中和的特征,将其余特征删除,进而更新矩阵和。
3.4 特征关联分析与选择
将处理好的、放入MT-SCCALR 模型,调整模型中的、、、、以及。具体调整方法为:
由于盲网格搜索十分的耗时,采用了一些相关方法来加速调整参数的过程。一方面,如果参数太小了,SCCA 和CCA 会产生相似的结果。另一方面,如果参数过大,SCCA将过度惩罚结果。因此,参数的选取不宜过大或者过小。用五折交叉验证的方法来寻找最优参数。使得测试集结果的相关系数最高的参数组合将被定为最优参数。公式如下。
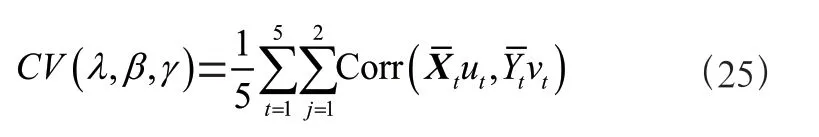
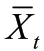
根据式(21)(24)可以得到每种目标在训练集和知识图谱中的权重向量u和v。将得到的每一个权重向量u取绝对值,然后按从大到小的顺序排列,按实际需要选取其中Top 特征,用于后续分类等。
4 结 论
本文提出了一种组合特征关联与选择方法,该方法通过JCB-SNMF 算法进行特征聚类和关联,通过MT-SCCALR方法进行特征选择,获得了更高的准确率。为目标的准确检测提供新见解。然而,该方法也存在一些不足。如基于SCCA 的方法具有较高的时间复杂度,对于较高维的数据特征关联分析较为困难。因此,在未来的研究中,需要对MTSCCALR 算法的目标函数求解进行进一步优化,降低时间复杂度。此外,我们也将尝试使用更多的数据集进行方法有效性验证。

