多环谐振微陀螺性能参数的有限元计算*

卢浩琳，张卫平，谷留涛，冯 军

（1.上海交通大学 微米纳米加工技术国家级重点实验室·上海·200240；2.上海交通大学 电子信息与电气工程学院 微纳电子学系·上海·200240）

0 引 言

陀螺仪作为一种惯性传感器，用于检测物体在惯性坐标系中转动的角度或角速度，是导航或制导系统的关键组成部分，在军事和民用领域均发挥着重要作用[1]。相较于三维陀螺仪[2-4]，基于微机电系统（Micro-Electro-Mechanical System，MEMS）技术制造的多环谐振微陀螺仪具有体积小、功耗低、成本低、可批量生产等优势[5-6]，因此受到了广泛关注。但是对于多环谐振微陀螺而言，由于结构较复杂，不易求解，其解析需要借助有限元方法（Finite Element Method，FEM）。

有限元方法的核心思想是离散化，即将一个连续体离散为有限个单元，通过求解各单元上的解，从而得到整个连续体的近似解[7]。有限元方法自提出以来，经过几十年的发展，已经成为工程应用中常用的一种数值计算方法。并且结合计算机技术开发的有限元软件也不断出现，例如 ANSYS、ABAQUS、COMSOL Multiphysics（简称 COMSOL）等[8-11],使用这些有限元软件可以很方便地求解一些复杂的大规模的工程问题。COMSOL 提供了许多预定义的物理场接口，具有强大的多物理场耦合计算功能。该软件最早源于 MATLAB 的Toolbox工具箱，目前仍提供与 MATLAB 协同计算的接口（COMSOL with MATLAB）。此外，它还提供 Microsoft Excel、SolidWorks、AutoCAD 等软件的接口，为了更方便地实现与这些软件之间的数据交流，本文主要基于 COMSOL 进行仿真模拟。

1 机械灵敏度与机械热噪声

1.1 机械灵敏度

机械灵敏度定义为检测轴方向的振动幅度与输入角速度之比，它表示微陀螺对于输入角速度的灵敏性，单位为m/（rad/s），其表达式为

（1）

其中，qA0=（QAF0）/kA，F0表示驱动力的幅度，kA表示驱动模态的振动位移；Ag为陀螺仪的角度增益；ωA、ωB分别为驱动模态和检测模态的谐振频率；QA、QB分别为驱动模态和检测模态的品质因子。当不存在频率裂解（ωA=ωB）时，机械灵敏度可以达到最大[12]

（2）

其中，ω0表示不存在频率裂解时的谐振频率，满足ω0=ωA=ωB；Q表示不存在频率裂解时的品质因子，满足Q=QA=QB。

1.2 机械热噪声

微陀螺的噪声包括由结构本身带来的机械热噪声和由测控电路造成的电学噪声[12]，如式（3）所示

（3）

其中，Ωoverall表示微陀螺的整体噪声；Ωmech表示机械热噪声；Ωelect表示电学噪声。陀螺仪的结构本身主要受机械热噪声的影响，其表达式为[13]

（4）

（5）

由式（1）、式（2）、式（4）和式（5）可知，要计算机械灵敏度和机械热噪声，需要求解陀螺仪的品质因子、频率裂解、角度增益和有效质量。

2 模态分析

微陀螺模型由SolidWorks 建立，结构参数标注如图1所示，包括谐振子半径R，中央锚点半径r，谐振环宽度Wr，辐条宽度Ws，辐条长度Ls，谐振子厚度H，电容间隙d0，谐振环数目N。

（a）俯视图

（b）侧视图图1 多环谐振微陀螺的结构参数Fig.1 The structural parameters of disk resonator gyroscope

本文研究了有限元仿真平台的搭建，对模型进行了一定简化，基于如下两点假设：

1）微陀螺为全对称结构，并且不存在加工误差，各个结构参数的取值如表1所示；

2）微陀螺的材料为各向同性的硅材料，其材料参数的取值如表2所示。

本文在没有特殊说明的情况下，都是基于以上两点假设进行计算的。

表1 用于有限元计算的结构参数取值

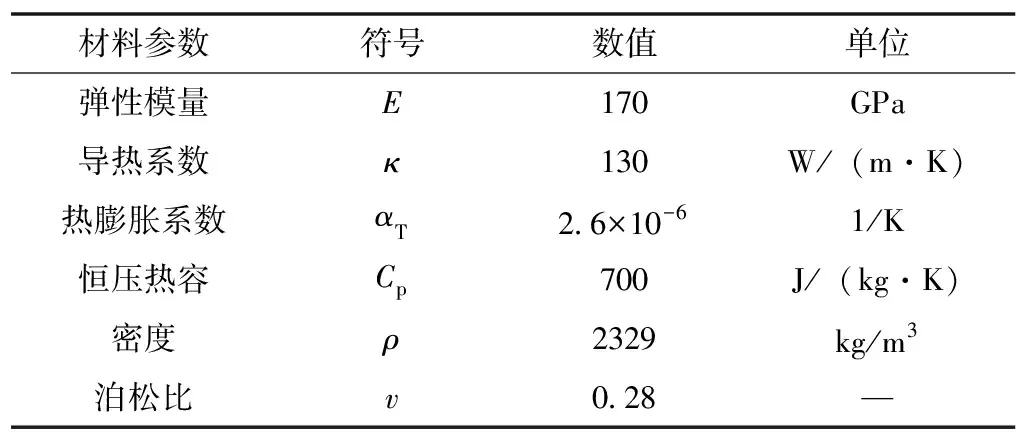
表2 用于有限元计算的材料参数取值

通过模态分析，可找出微陀螺的四波腹工作模态及其谐振频率。从数值求解的角度来看，模态分析本质上是求解矩阵的特征值。根据实际有限元模型的求解需求，选择合适的特征值求解方法可以有效地提高求解过程的收敛性和运算效率。对微陀螺进行模态分析需要添加特征频率研究，四波腹模态的谐振频率约为22kHz，因此可将特征频率的搜索基准值设置为附近的18kHz，所需特征频率数设置为4个，并从基准值开始往更大的频率进行搜索。由于多环微陀螺具有高度对称性，使用三角形与扫掠相结合的网格划分方法可以实现高精度和高速度的计算。此外，相较于Z轴方向而言，XY平面内的网格细化程度对结果的影响更明显。本文将优先采用自由三角形与扫掠相结合的网格划分方法，并且重点关注XY平面内的网格细化程度。图2所示为使用COMSOL进行模态分析求解得到的n=2模态振型。

图2 COSMOL 求解n=2模态的振型Fig.2 Vibration shapes of n=2 mode in COMSOL

3 有效质量与角度增益的求解

完成模态分析之后,即可求解有效质量和角度增益。COMSOL中没有预设的求解器对有效质量和角度增益进行求解，因此需要找出有效质量和角度增益的有限元计算公式。引入一个表征模态形状的参量——振型函数。振型函数定义为该振型中某个单元的位移与所有单元的最大位移（即波腹点位移）之比[14]。对于驱动模态而言，某一单元x、y、z三个方向的振型函数可分别表示为

（6）

其中，u1、v1、w1分别表示驱动模态每个单元在x、y、z三个方向上的位移；q1表示驱动模态的波腹点位移。同理，对于检测模态而言，振型函数可表示为

（7）

其中，u2、v2、w2分别表示检测模态每个单元在x、y、z三个方向上的位移；q2表示检测模态的波腹点位移。

文献[6]给出了有效质量和角度增益的计算公式，分别为式（8）和式（9）。式（8）事实上是驱动模态的有效质量， 理想情况下检测模态的有效质量可由式（9）表示。当考虑微陀螺的不对称性时，求解检测模态的有效质量则需要将式（8）中的振型函数用式（7）替代

（8）

（9）

其中，V表示微陀螺的体积；n表示模态阶数。定义科氏质量γcor为

（10）

则角度增益与有效质量以及科氏质量的关系为

（11）

对于有限元模型，式（8）和式（10）可写成如下离散形式

[φz1（i）]2}δV（i）

（12）

φx2（i）φy1（i）}δV（i）

（13）

其中，δV（i）表示第i个单元的体积；Ne表示单元的总数目；i=1,2，…，Ne表示第i个单元。要求出有效质量和角度增益，应该先提取每个单元的位移，然后求出其振型函数，再对振型函数进行体积分求得有效质量和角度增益。

根据上述分析，求解有效质量和角度增益的关键在于提取各网格单元的位移、体积等数据。MATLAB 与COMSOL可以实现很好的协同计算，因此可以采用MATLAB提取COMSOL有限元模型的节点数据，并在MATLAB中对这些节点数据进行处理和计算。本文采用COMSOL with MATLAB进行计算。计算过程如下：

第一步，在COMSOL中进行模态分析。由于前面已经得到特征频率较精确的值，因此在该值附近提取特征频率，可以设置所需特征频率数为2，得到的二阶模态分别对应驱动模态和检测模态。

第二步，通过MATLAB的mpheval命令提取节点数据，需要提取的节点数据包括x、y、z方向的位移以及体积。使用mpheval命令在 MATLAB 中存储一个结构体，该结构体包括：d1为所计算表达式在每个节点处的结果（如位移、体积） ；p为节点的坐标；t为与节点坐标对应的节点列索引，其每列对应于这些节点所构成的一个网格单元，因此t的列数就是网格单元的个数，t的行数是网格单元对应的节点数；ve为每个节点的网格单元索引；unit为所计算表达式的单位。

第三步，采用节点平均法对节点数据进行处理。由于MATLAB提取出来的是节点数据，并不是网格单元的数据，因此需要将节点数据转化为单元数据。每个网格单元由多个节点构成，通过求解这些节点数据的平均值可以得到对应网格单元的数据。该步骤的一个关键点在于如何将节点与单元对应起来。由于上述结构体中的列索引t存储了每个单元对应的节点，因此只需要依次求解t中每一列所有节点数据的平均值，即可得到每个单元数据的值，其中节点数据的值可以由d1得到。

第四步，通过前面三个步骤已经得到每个单元的数据（位移与体积），接下来只需要根据式（11）、式（12）和式（13）即可求解有效质量和角度增益。

这里给出了三种求解meff的方法和两种求解Ag的方法。

3.1 求解meff

方法1：提取每个单元在x、y、z方向的位移以及波腹点位移，求出每个单元的振型函数，然后根据式（12）即可求出meff。

方法2：将驱动模态和检测模态所有单元的总位移分别构成列向量d1和d2，所有单元在x、y、z方向的位移分别构成列向量u1、v1、w1和u2、v2、w2， 所有单元的体积构成列向量δV。根据式（8）可得

（14）

其中，diag运算表示以向量的形式返回矩阵上的对角线元素。

方法3：式（8）可以改写为

meff=λmMreal

（15）

其中，Mreal定义为微陀螺的实际质量。有效质量的大小为实际质量乘以一个系数λm，其表达式为

（16）

将λm定义为有效质量系数，表示有效质量占实际质量的比例。可以看出,它是一个与模态形状有关的量，与波腹点位移相近的单元数越多则λm越大。通过该方法求解有效质量,需要先求解微陀螺的实际质量Mreal和总体积Vtotal。

3.2 求解Ag

方法1：提取每个单元在x、y、z方向的位移以及波腹点位移， 求出每个单元的振型函数， 然后根据式（6）、式（7）和式（8）即可求出Ag。

方法2：与求解meff的方法2类似，角度增益可以由式（17）求出

（17）

采用非结构化的自由四面体单元进行网格划分，单元大小设置为极细化，计算结果汇总于表3。 求解Ag的两种方法在结果上有些许差异， 但这种差异是由于计算机精度造成的误差，在合理范围内。

当采用自由三角形与扫掠相结合的网格划分方法时，利用上述方法进行计算，得到的结果为：meff=7.3469×10-7kg，Mreal=2.3232×10-6kg，Vtotal=9.9753×10-10m3。这与表3的结果有很大差异， 并且Vtotal的值与实际值不一致（COMSOL 与SolidWorks 中测量得到的实际模型体积为 0.3324mm3），这说明该计算结果不正确。通过分析发现，此时结构体中的t仍然是4行的矩阵，t的列数与实际的网格单元数也不相等。这说明此时在 MATLAB 中，每个网格单元仍被视为四面体单元，这与实际情况是不相符的。事实上，当采用部分结构化网格进行划分时，每个单元为三棱柱结构，而并非四面体结构。 因此COMSOL with MATLAB协同计算仅仅适用于自由四面体单元的非结构化网格划分。

通过前文分析可知，在相同的精度下，采用非结构化网格的计算量和计算时间远远超过部分结构化网格。COMSOL with MATLAB协同计算只限于非结构化网格划分，将造成计算缓慢且内存需求很大。若利用COMSOL单独计算，可不受网格划分方式的限制。因此，有必要研究单独利用COMSOL计算有效质量和角度增益的方法。

COMSOL提供了一个可提取模型中任意解的算子withsol，该算子既可用在计算过程中，也可以用在数据的后处理当中，使用起来特别方便。例如，使用“withsol（′sol1′,expr,setind（lambda,1））” 命令,即可提取第一阶模态的表达式，其中setind用于控制所提取数据的模态阶数，expr表示所要提取的表达式（x、y、z方向的位移、 波腹点位移、 体积等）。 采用withsol算子设置如下几个变量：波腹点位移、振型函数、有效质量、角度增益。其中还需要定义两个算子：最大值算子maxop1，用于提取波腹点位移；积分算子intop1， 用于进行积分运算。 同样采用部分结构化网格进行划分， 计算结果为：meff=2.4489×10-7kg，Ag=0.3958。 该结果与前文基于COMSOL with MATLAB的计算结果基本一致，其差异是由于网格划分方式不同造成的。

相较于COMSOL with MATLAB协同计算，采用COMSOL单独计算不受网格划分方式的限制，可以提高计算精度和计算速度。

4 品质因子的求解

由于品质因子可以由热弹性品质因子来表示，因此求解品质因子等同于求解热弹性阻尼。研究热弹性阻尼需要同时添加力学场和热学场，COMSOL中的热弹性力学物理场耦合了固体力学与固体传热，可以用于热弹性阻尼的分析。同时添加热扰动和特征频率研究，初始温度T0设置为室温293.15K，热量来源于热弹性阻尼[15]。

COMSOL内置耦合热弹性方程，并将热扰动下的特征频率用复数表示，利用前文所述的复频率方法可以得出热弹性品质因子QTED，求解得到QTED的值为72418。同时，COMSOL还可以求得微陀螺仪中的温度分布，如图3所示，由于各处温度分布不均匀，导致了振动能量以热流的形式耗散。

图3 多环谐振微陀螺中的温度分布Fig.3 Temperature distribution in the disk resonator gyroscope

5 结 论

本文主要介绍了多环谐振微陀螺性能参数的有限元计算方法。 在陀螺仪基本研究的基础上，搭建了基于COMSOL 和 MATLAB 等软件的有限元计算平台，实现了对谐振频率、有效质量、角度增益和品质因子等性能参数的有限元求解。并且这些性能参数既可由 COMSOL with MATLAB 协同计算，也可由 COMSOL 单独计算。本文搭建的有限元计算平台为研究微陀螺结构的性能参数和优化设计提供了有力的工具。