高精度UWB的室内无线定位关键技术研究

王明涛， 汪文元， 叶亚林， 卢玉龙， 汪广明， 何滔

(国能大渡河沙坪发电有限公司，四川 乐山 614300)

0 引 言

无线信号在传播途中受到墙壁遮挡出现反射和衍射的情况，信号发生不同程度的衰减和时延扩展，给室内定位服务带来困难[1-2]。文献[3]利用超声波进行定位，通过反射测量锚节点和用户之间的距离，从而实现对用户进行定位。但在室内环境中出现严重的多径效应，信号发生衰减影响用户定位的精度。文献[4]提出Buletoth室内定位方法，蓝牙发射功率较小且易于集成，通过蓝牙节点的信号强度估计用户节点的位置。但在复杂的室内环境下噪声影响系统的稳定性，接收到信号中含有噪声分量。

针对上述研究中存在的不足，本文分析了超宽带(ultra wide-band，UWB)信号的时域特征和频率特征，针对室内环境中的多径信道提出改进的时延估计算法，并扩展卡尔曼滤波器对室内用的未知节点进行精准定位。

1 三维时空数据库的地信时空可视化技术

本文的创新点在以下两点。

(1) 基于UWB的TOA(time of arrival)估计检测参考节点的到达时延，根据多个参考节点对用户进行定位。通过能量接收机的带通滤波模块去除UWB信号每帧的噪声分量，引入校验窗多次判决提高了噪声信号的检测能力。

(2) 使用非线性函数扩展卡尔曼滤波器，并对用户的状态向量和测量向量的值进行校正，解决了非视距误差对用户定位精度的影响，减小了定位误差。

基于UWB的室内无线定位服务架构，如图1所示。

图1 基于UWB的室内无线定位服务架构

本文采用TOA估计测距时对用户定位的精度更高。根据用户和参考节点建立的联系，以参考节点为中心划分出圆形区域包围未知节点，通过另一端的参考节点测量信号的传播时间，产生第二个圆形区域。两个参考节点的圆形区域的两个交点与用户的未知节点建立联系，测量出第三个参考节点的传播时间，得到另一个区域求解未知节点的位置[5]。TOA测量参数节点接收信号的达到时延或基站确定用户未知节点的信号路径时间，并且用户未知节点和参考节点的时间同步。信号的同步时间精度不高导致各个参考节点接收到信号的时延与实际信号传输时延不一致，将会产生较大的定位误差[9]。超宽带信号使用的间歇脉冲持续时间范围是(0.2 ns，1.5 ns)，由于室内环境下多径传播影响了连续信号或持续时间较长的信号的质量，而超宽带信号可以分离出多个多径分量和发生信号的分量，UWB无线信号的衰落不超过5 dB，在室内对用户的未知节点进行定位的精度更高。

2 关键技术设计

2.1 基于UWB信号的能量检测TOA估计

由于UWB信号在传输过程中受到大量噪声分量的影响导致接收端不容易检测出有用信息。同时在室内环境下出现大量的反射、衍射的多径成分，噪声信号和多径干扰影响了UWB时延估计精度。本文基于能量接收机TOA估计，最大化利用接收信号的特征提取更多的有用信息[6]。

TOA估计用来检测参考节点直达路径和第一路径的到达时延，检测算法可以在时域和频域中展开，对接收信号进行一种线性或非线性的转换，用来识别参考节点的第一路径和噪声信号和多径信号成分。设定用户未知节点发射端与参考节点接收端时间同步，采用连续的UWB脉冲作为发射信号，可表示为：

(1)

式中：Nf为测距符号中的帧数；Tf为帧周期；ES为测距符号的能量；τg为帧信号的保护时隙，用来预防帧间干扰，发射脉冲为高斯脉冲。

w(t)=(1-4πt2/θ2)

(2)

经过多径信道传输后，参考节点接收信号可表示为：

(3)

式中：K为多径信号成分的数量；ak为幅度；τk为到达时延；nc为高斯白噪声。能量接收机如图2所示。

图2 能量接收机模块

其中带通滤波器用来去除UWB信号的带外噪声，参考节点接收到的信号经过滤波后再经过平方律积分模块处理，采样得到用户未知节点信号的能量样本。采样第n帧信号的第i个样本可得到：

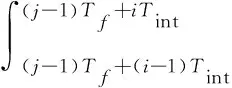
(4)

式中：rbpf(t)为经过带通滤波器的UWB信号；Tint为采样周期。每帧参考节点信号可以得到Tf/Tint个能量样本[7]。UWB信号到达参考节点的每帧信号中噪声能量样本随机分布。由于参考节点的接收特性，在连续的能量样本上引入校验窗，对现有各能量样本独立判别并验证。采用虚假检测准则选取接收信号的能量阈值，可表示为：

ηa=σnQ-1(Pfa)+μn,n=1,2,…,Nf

(5)

式中：Pfa为虚假概率，Pfa越大得到的信号能量阈值出现减小的趋势；σn为接收信号中噪声样本的均值；μn为噪声样本的方差；Q-1为正态逆累积函数。将接收信号的判决变量序列与阈值进行比较，得到的判决结果记录在Ui中，采用滑动窗后的判决变量可表示为：

(6)

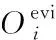
ηw=TNw

(7)

式中：T为权重因子；Nw为滑动窗的宽度。经过滑动窗的二级判别后，完成FP检测，接收到的信号为可信的能量样本。

以上TOA估计算法与第一个滑动窗内的能量样本有关，整个过程包括两次阈值判决，第一次为粗略的判决检测，第二次通过连续的多个能量样本联合检测得到的检测精度更高，提高对参考节点接收到UWB信号中噪声信号的检测能力。

2.2 扩展卡尔曼滤波器

在对用户未知节点进行定位时，室内环境下复杂的信道环境影响了测量精度，给用户定位非线性问题时带来了误差。实际室内空间中存在大量的障碍物和遮挡物造成多径干扰，对用户未知节点测距时造成非视距误差。在实际定位服务应用中，大多数都是非线性问题，本文使用卡尔曼滤波器估计动态系统的状态[9]。

卡尔曼滤波器的状态方程和测量方程可表示为：

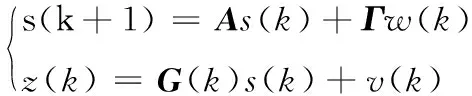
(8)

式中：s(k)为用户的状态；z(k)为用户节点的测量值；A为采样转移矩阵;Γ为噪声矩阵;G(k)为测量矩阵；w(k)、v(k)为噪声分量。给定了状态向量和估计误差的协方差后通过迭代评估用户的状态向量。第一步状态预测可表示为：

(9)

第二步校正用户的测量值，可表示为：

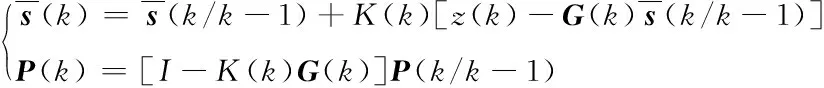
(10)

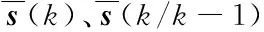
基本的卡尔曼滤波器只能在存在线性噪声的高斯模型的理想状态下使用，要解决实际室内环境下无线定位非线性问题，采用非线性函数的局部特征近似非线性[10]。第k时刻用户的坐标为(xk,yk)，参考节点或基站坐标为(xi,yi)，估计状态为[xk,yk]T，系统状态方程和测量方程可表示为：

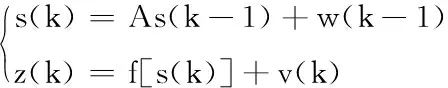
(11)

式中：f[s(k)]为非线性变换函数。在k-1时刻向k时刻转换时，使用泰勒级数展开，可表示为：

(12)

w(k)、v(k)的协方差矩阵分别为Q和R，列数为2，迭代方程为：

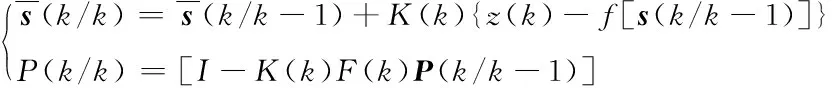
(13)

基于到达时间差(time difference of arrival,TDOA)的扩展卡尔曼滤波器，测量TDOA值。将测量方程中的非线性变换改为用户未知节点和参考节点的到达时延和预测值，根据上一时刻的用户状态实现了对用户的精准定位，减少了非视距误差对定位精度的影响。扩展卡尔曼滤波算法仿真如图3所示。

图3 扩展卡尔曼滤波仿真图

图3中:A曲线表示标准差为0.15时的定位误差变化；B曲线表示标准差为0.25；C曲线表示标准差为0.35。随着仿真次数的增加，对用户未知节点的定位精度逐渐增加，定位误差逐渐减小为0。

3 应用测试

为验证本文高精度UWB的室内无线定位系统的性能，分别使用文献[3]方法、文献[4]方法和本文方法定位系统进行试验，对比三种系统的定位精度和定位误差。

用户需携带定位设备不断发出射频信号，参考节点天线接收到用户发出的UWB信号，测量信号的到达时延并记录到达时间戳，同步用户未知节点和参考节点的时间。用户定位设备工作频率为1 Hz～100 Hz。

本文试验环境为60 m×80 m的室内空间，室内环境均匀配置9个参考节点，在室内随机放置用户进行定位。试验环境如图4所示，阴影部分为障碍物遮挡。

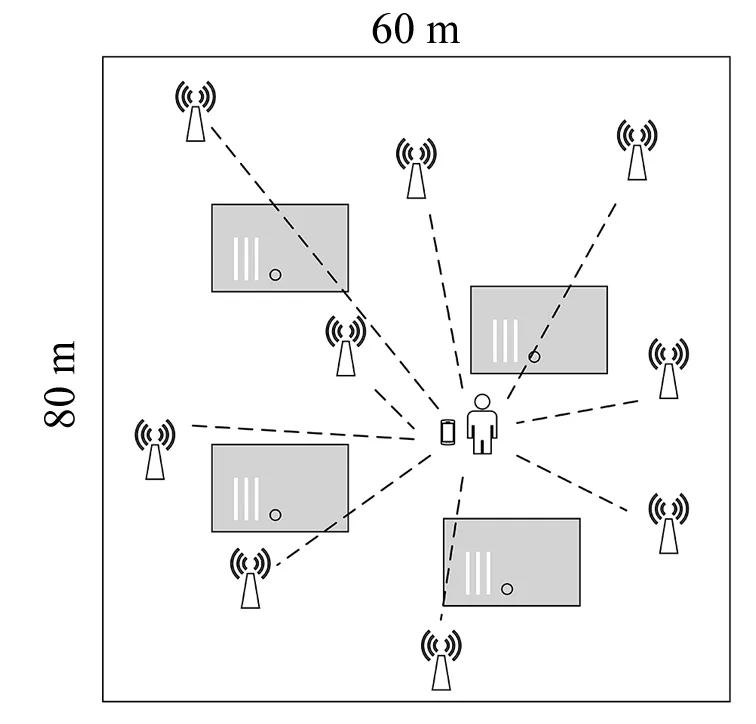
图4 室内无线定位试验环境

使用三种定位系统对用户固定位置时进行定位测量，得到的位置信息和定位误差如表1所示。

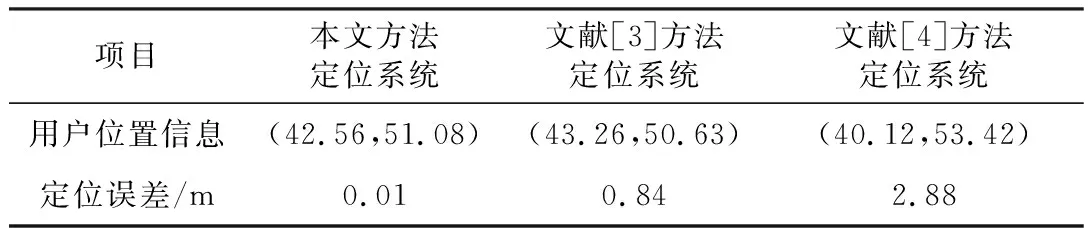
表1 定位结果

对比三种定位系统对用户的定位误差可知，本文研究的高精度UWB室内无线定位系统的定位精度最高，定位误差最低达到0.01 m。UWB信号在室内环境下信道传输过程中对信道衰落不敏感，抗干扰能力较强，且通过卡尔曼滤波器减少接收端信号的噪声分量。文献[3]方法定位系统的定位误差达到0.84 m，虽然能够定位到用户的大致位置，但不适用于高精度的定位服务。文献[4]方法定位系统的定位误差为2.88 m，定位误差高于2 m。说明文献[4]方法受到室内信号多径传播的影响，同时噪声影响接收到用户信号的质量，从而影响对用户的定位精度。

测量用户保持运动状态时的定位误差，控制用户运动速度为1.1～1.5 m/s，根据三种系统的定位结果得到均方根误差，选择300个采集到的位置信息与真实位置进行比较，采样点的均方根误差如图5所示。

图5 采样点均方根误差

根据三种定位系统的采样点均方根误差变化曲线可知，本文方法对室内用户的定位精度更高，均方根误差变化幅度不明显，定位误差趋近于0。文献[3]方法定位系统对运动中用户位置的定位误差总体保持在1 m以下，采样点均方根误差最大达到1.1 m，变化幅度不大。文献[4]方法定位系统的定位误差最大为2.93 m，定位系统不稳定，均方根误差上下幅度最大达到0.51 m。说明受到较大非视距误差的干扰，定位精度较差。

4 结束语

本文采用纳秒级的极窄脉冲的UWB信号来传输数据，穿透性更强且抗多径效果好，并分析了UWB信号特征，提出改进的时延估计算法对用户未知节点进行定位。在参考节点能量接收检测下引入校验窗，判决多径信号成分，获取额外的性能增益。

本文在二维平台对三维空间场景中的用户位置进行研究，以后的研究方向可以向3D场景发展，并针对特殊的3D空间进行扩展应用。