基于机器学习的海上蒸发波导特性智能化预测

石广亮 杨 铖 王 健,3

1.天津大学微电子学院 天津 300072 2.天津大学青岛海洋技术研究院 山东青岛 266200 3.电子信息系统复杂电磁环境效应国家重点实验室 河南洛阳 473003

作战决策是海上编队作战任务规划业务乃至整个作战指挥活动的核心,其前提是有效地掌握和应用海上作战环境[1].海上作战环境特性的预测是系统论证设计[2-3]、指挥控制、占领电磁环境与频谱战优势[3]的重要基石.海上是大气波导的多发地带,在海上大气波导几乎是永久性出现的.大气波导是影响海上作战和辅助决策的重要因素,也是低空无线信道的重要组成部分[4].作为海上大气波导的一种重要形式,蒸发波导是在特定气象水文条件下海气相互作用引起的海面水汽蒸发,海面上大气湿度随高度锐减造成的较大的湿度垂直梯度变化,所形成的一种海洋大气边界层内的底层大气结构.蒸发波导在世界各大海洋环境及其沿海地区几乎是永久出现的[5],并且它对雷达和通信等无线电系统的海上应用和作战指挥具有重要影响.

常用的蒸发波导预测模型有BYC（babin young carton）模型,P-J（paulus-jeske）模型,NPS（naval postgraduate school）模型,Gerstoft 多参数模型,伪折射率模型,MGB（musson-gauthier-bruth）模型[7-11].上述传统的蒸发波导预测模型的建立与更新均依赖于边界层理论的发展和不同的大型现场实验[12-16].其中,文献[12]在Monin-Obukhov 相似理论背景下,对各种稳定条件下的风和温度轮廓线进行了分析.文献[13]提出了一种用于表示预报模式中热、动量和水汽垂直涡动通量的方案,该方案的一个重要特点是扩散系数依赖于大气的静态特性.文献[14]建立了一种包括海气界面两侧的界面亚层在内的海洋大气层模型.文献[15]对地球表面的数值天气预报系统提出了一种新的数据插值方法.由于受边界层理论基本假设的影响,传统预测模型的准确性和应用存在着一定的局限性.

在上述研究成果的基础上,近年国内外学者引入了人工智能方法用于提升模型的可用性.2008年,Douvenot 等通过支持向量机反演方法,并利用传播损失和相应参数值预生成数据库,但是预测精度欠佳[17-18].2017年,Tepecik 和Navruz 等使用神经网络的参数估计作为遗传算法的初始化器实现了反演[19].2018年,Zhu 等使用支持向量机方法对P-J 模型进行改进,得到了一种SVR P-J 模型,改进的SVR P-J 模型预测精度有所提高[20].结果表明,人工智能的方法在蒸发波导参数预测领域行之有效,并且能够带来一定的应用效益.分析发现,上述模型受物理假设的约束,预测精度方面还需进一步的提升.

当前,海洋信息化作为我国国家信息化发展的一个重要方面,正步入重要的战略机遇期.面向海上无线电系统设计、作战指挥和装备应用保障,蒸发波导的精确预测和智能应用将成为海洋作战指挥的完善长板,对于占领电磁环境和频谱战优势、支撑海上作战具有重要意义.同时,考虑到机器学习是一种获取数据潜在规律的有效方法,所得到的规律完全基于训练数据,不受边界层基本假设的约束,且能够给出模型的具体表达式,因此,它能最大程度地挖掘数据的规律,贴近物理特征的变化形态.本文基于机器学习形成了一种重建蒸发波导预测模型的方法.首先,对中国南海典型海域全年不同高度下对应的大气折射率剖面数据进行反演,然后对其进行回归学习,并确定了3 个最优参数,最终重建了多参数模型,并将其与传统模型进行对比.区别于传统预测模型受物理假设的约束,该模型完全基于实测数据.

1 建模方法

机器学习通过数据和统计学方法来提高系统性能,是人工智能领域一个重要分支和研究热点.在现有的数据集的基础上,通过依次确定机器学习模型、机器学习策略以及机器学习算法找到最优模型,可用于预测数据的未来状态.此外,机器学习还可以解决很多问题,例如可以发现数据的某种共同性质或者规律,模型就是用来体现这一规律性.对全年修正大气折射率剖面数据分析发现：修正大气折射率在不同的时间具有一定的规律性.对于预先确定的假设空间,机器学习是从所有模型集合的假设空间中找到某一确定的最优模型.因此,本文将已知的修正大气折射率和对应的高度作为假设空间,并在该假设空间内选择最优模型.通过机器学习得到最优模型对应算法,并依次确定不同时间的最优模型.在寻找最优模型解的过程中,还需要对假设空间里的所有模型定义一个评价标准,然后由最优化算法根据评价准则从假设空间中选出最优的模型.

对于机器学习,首先模型选择是最为关键的过程,本文选择了Gerstoft 多参数模型去预测蒸发波导的高度.该模型参数化地表示了可能出现的蒸发波导,只要给定3 个参数就可以确定修正大气折射率剖面随高度变化的函数值,从而得到此时的蒸发波导情况.该模型得到了较为广泛的应用,同时该模型参数化的反演方法,为基于智能算法与实测数据的可靠实现提供了算法优化基础环境[21-23].分析可知：该模型参数具有多种组合,故假设空间也有多个.然后本文采用均方根误差（root mean square error,RMSE）作为评价标准选取最优参数,从而得到最优模型.最后确定计算模型的具体计算方法,基于训练的数据集,根据“均方根误差最小”的策略从3 个参数的假设空间中选出最优模型,在已知代价函数的基础上求解模型参数,得到修正大气折射率,作出修正大气折射率剖面,预测蒸发波导的高度.

训练模型的数据是基于最新的国家大气研究中心（National Center for Atmospheric Research,NCAR）全球气象同化数据库中的地表气象参数[24].通过NPS模型得到不同高度下的修正大气折射率剖面数据作为模型的测试数据和训练数据,并将此数据作为机器学习的输入,输出为最优参数组合.在使用机器学习之前,需要对该数据初步特征进行分析,反演大气折射率剖面,去除异常剖面,分析蒸发波导特性参数.再采用均值和中值的方法对该数据进行预处理,并对比数据变化趋势.根据假设空间已知参数和目标参数,确定选择多参数蒸发波导预测模型.使用机器学习的方法重建模型,根据评价准则从假设空间确定蒸发波导的厚度t、混合层斜率k 和临界高度hc最优参数,得到不同时刻下的修正大气折射率剖面,预测蒸发波导的高度.机器学习重建蒸发波导模型流程图如图1所示.

图1 机器学习重建蒸发波导模型流程Fig.1 The process of machine learning reconstructing evaporation duct model

本文使用统计机器学习的方式来重建蒸发波导预测模型.根据统计机器学习的思想,重建了计算修正大气折射率剖面的模型,并建立了季节、月份、时刻与其之间的关系.

2 模型重建

2.1 建模数据

选用NCAR 全球气象同化数据库中的地表气象参数,该数据库是对源于卫星、飞机、无线电探空气球、地面、船舶等气象观测资料进行同化处理后,公开发布的全球气象资料数据库,具有分布范围广,分辨率高的特点.本文选择南海海域北部、海南省沿海区域作为代表开展研究.文中获取了该区域2018年和2019年的NCAR 气象遥感数据,主要包括温度、湿度和大气压等气象参数,使用NPS 模型得到分析位置修正大气折射率剖面,据此开展蒸发波导时间特性的统计规律分析.根据蒸发波导特性,在0～40 m 范围内,以0.1 m 取样间隔,分析不同高度下每小时的大气折射率具体数据,将通过NPS 模型计算出来的不同高度下的大气折射率M 所构建的剖面及计算的蒸发波导高度作为模型重建的数据输入.

在对中国南海海域大气折射率剖面数据的分析与处理中,首先去除实测数据中部分异常大气折射率剖面,从而得到大气折射率剖面Mfact.然后根据大气折射率剖面梯度变化拐点即蒸发波导高度这一理论,对Mfact处理进而得到的蒸发波导的高度hfact,并去除hfact中异常数据.最后对每个月的同一时刻取平均值,统计共得到12 个月对应的24 个不同时刻下288 个蒸发波导的高度.原始数据处理流程如图2所示.

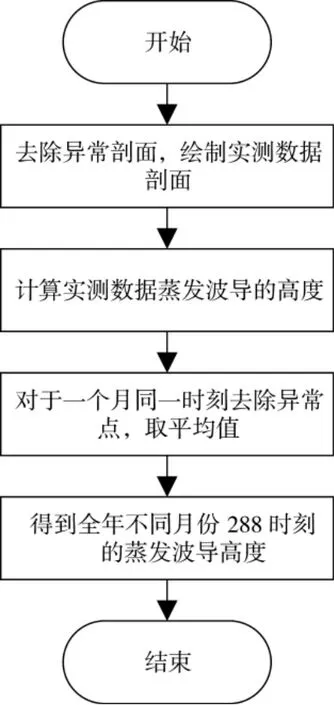
图2 原始数据处理流程Fig.2 Original data process flow

2.2 初始模型

Gerstoft 多参数模型适用于气候稳定、年平均温湿度数据变化稳定的区域.分析表明,研究地区在1959年-2015年年均温湿度数据变化稳定,同时该地区在近50年来未出现过热浪[25].故选择此区域数据作为模型重建基础,以实现区域化蒸发波导模型的重建.

修正大气折射率对蒸发波导的研究至关重要[26].Gerstoft 提出的多参数模型是关于蒸发波导应用比较广泛的一种模型[9].在众多蒸发波导模型中Gerstoft多参数模型是一个最直接计算修正大气折射率的模型.Gerstoft 多参数模型的输入是垂直高度h,输出是修正大气折射率M,通过不同高度下的修正大气折射率数值绘制大气折射率剖面,进而确定大气折射率剖面梯度变化的拐点,即为蒸发波导的高度.

为了参数化地表示海面上可能出现的蒸发波导,参数用矢量表示为

模型所需确定的3 个参数分别是：蒸发波导厚度t,混合层斜率k 和临界高度hc.

用于蒸发波导的折射率曲线可以被建模为在高度范围方向上假定均匀的对数线性函数.该模型主要涉及到一个表层的蒸发波导剖面,其蒸发波导的剖面可以用以高度h 为自变量的修正大气折射率函数表示

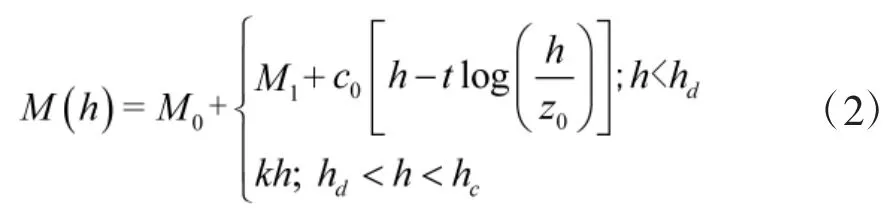
式中,h 是垂直高度；粗糙度因子z0=0.000 15[9]；混合层修正折射率梯度c0=0.13 M units/m[27],对应于中性折射曲线[28]；蒸发波导的厚度t 取0～40 m[9]；混合层斜率k 取-1 M units/m～0.4 M units/m[9]；临界高度hc取40 m～60 m[9]；M0是基础折射率,也可以理解为M 轮廓的偏移,一般取330 M[9].

M1可以表示为

hd为蒸发波导的高度,可以表示为

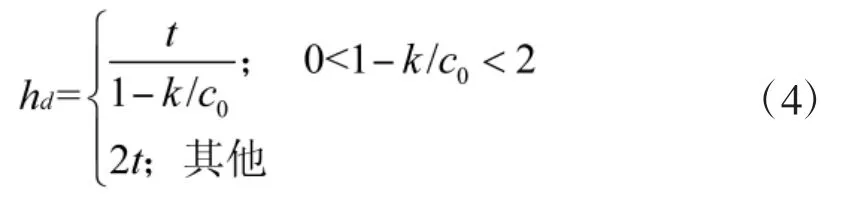
只要给定3 个参数值就可以确定大气折射率剖面,从而得到此时蒸发波导的情况.基于Gerstoft 多参数模型大气折射率剖面反演技术得到的反演值与实际测量值在有效范围内拟合较好,因此,使用Gerstoft 多参数模型反演大气折射率剖面技术在蒸发波导预测上得到了广泛的应用.此模型克服了海上大气折射率剖面难于测量的困难,还具有实时、便捷、易行的特点[21].

2.3 模型重建

本文采取均方根误差最小的方式来挑选参数最优模型,从而确定计算模型的具体计算方法.基于训练的数据集,根据误差最小的策略从3 个参数的假设空间中选出最优参数对应的最优模型,在已知代价函数的基础上求解模型参数,采用最小二乘回归分析方法求解大气折射率,并作出大气折射率剖面,预测蒸发波导的高度.

根据模型M（h）得出,这3 个参数t、k、hc共同决定了修正大气折射率M 的取值.其中,

根据Gerstoft 多参数模型的范围,可知

然后对实测数据每个月同一时刻不同高度下的蒸发波导高度取平均值hfact,并将其与在N 种组合下计算出来的修正大气折射率剖面得到的蒸发波导高度hmodel进行比较,选择均方根误差最小的组合.进而可得

均方根误差（RMSE）通常用于衡量回归任务中回归输出值与目标值之间的偏差,数值越低,则预测

效果较好,其计算方法如下

式中,n 为样本总数；hfact为蒸发波导的实际高度,hmodel为模型计算出来的蒸发波导高度.

对于kopt、hc_opt、topt,本文得到每个月份的24 种组合,全年共计288 种组合.统计机器学习算法流程图如图3所示.

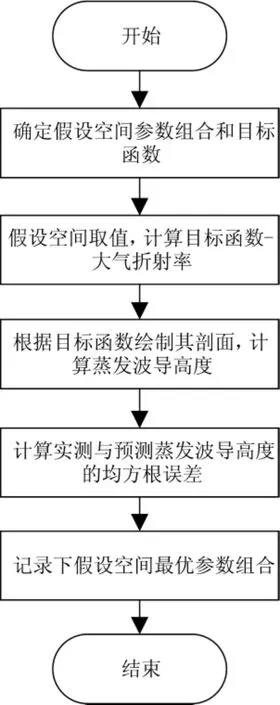
图3 算法流程图Fig.3 The algorithm flowchart

根据文献[9]确定了临界高度hc的范围为40 m～60 m、混合层斜率k 的范围为-1～0.4,依据相应范围对应训练出hc取值为40 m、k 取值为0.090 5.此外,根据文献[9]还确定了蒸发波导的厚度t 的取值范围为0～40 m,本文参数t 出现了288 种组合,它与月份g、时间h 组成了以下平面t（g,h）,如图4所示.

图4 波导厚度训练结果时变特性Fig.4 The tempral characteristics of duct thickness training results

通过使用实测数据训练的Gerstoft 多参数模型,本文利用线性回归的方法确定出3 个参数的取值.在全年不同月份不同时间下,临界高度hc=40,混合层斜率k=0.090 5,蒸发波导的厚度t 训练结果随时间和月份变化的特性平面如图4所示.通过得到的参数对比发现,在春季（12月～2月）,夏季（3月～5月）,秋季（6月～8月）,冬季（9月～11月）具有一定的季节规律性.

3 分析讨论

根据机器学习算法,利用所得模型可预测2020年该海域不同高度下的修正大气折射率M 的取值,图5给出了春、夏、秋、冬四季典型时刻的实测大气折射率剖面与本文模型给出的大气折射率剖面对比的结果.可以看出：本文模型计算大气折射率剖面与实测数据大气折射率剖面变化趋势吻合较好.预测剖面偏差如表1所示.

表1 本文模型预测剖面与实测数据剖面偏差Table 1 The deviation between the model predicted profile and the measured data profile

图5 不同季节实测剖面与本文模型预测剖面对比Fig.5 Comparison between measured profiles in different seasons and predicted profiles in this paper

通过对大气折射率剖面分析,进一步可得蒸发波导高度预测值与实测值对比情况,如图6所示.从图中可以看出：

图6 不同预测模型值与实测值的对比Fig.6 Comparison of the predicted height with the actual height of evaporation duct

1）模型值与实测值的变化规律有较好的一致性,且均为夏季平均值较低、冬季较高,春、秋两季介于冬、夏两季之间,此外,数值普遍为上午高于下午.

2）本文模型较Gerstoft 模型更为接近实测值,具体误差对比将在后面进一步分析.

春季、夏季、秋季和冬季4 个季节的不同时刻的预测误差如图7所示.从图中可以看出：

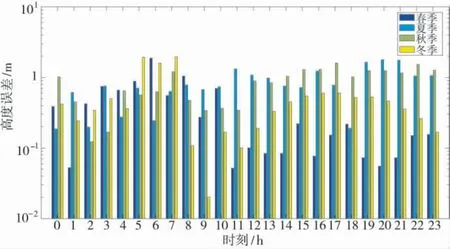
图7 预测偏差的不同时段的分布规律Fig.7 The distribution of predicted deviation in different periods

1）模型值和实测值之间预测的蒸发波导高度误差均在2 m 以内,因此,对电磁波传播预测误差影响较小.

2）本文模型在春季和冬季的凌晨与下午误差较小,预测精度较高.夏季和秋季全天24 h 整体误差较小,预测精度整体较高.

使用本文方法重建的蒸发波导预测模型,在中国南海海域地区预测准确率较高,对比传统模型,其对应的RMSE 如表2所示.结果表明,本文模型比Gerstoft 模型均方根误差更小,预测精度更高.

从表2可以看出：

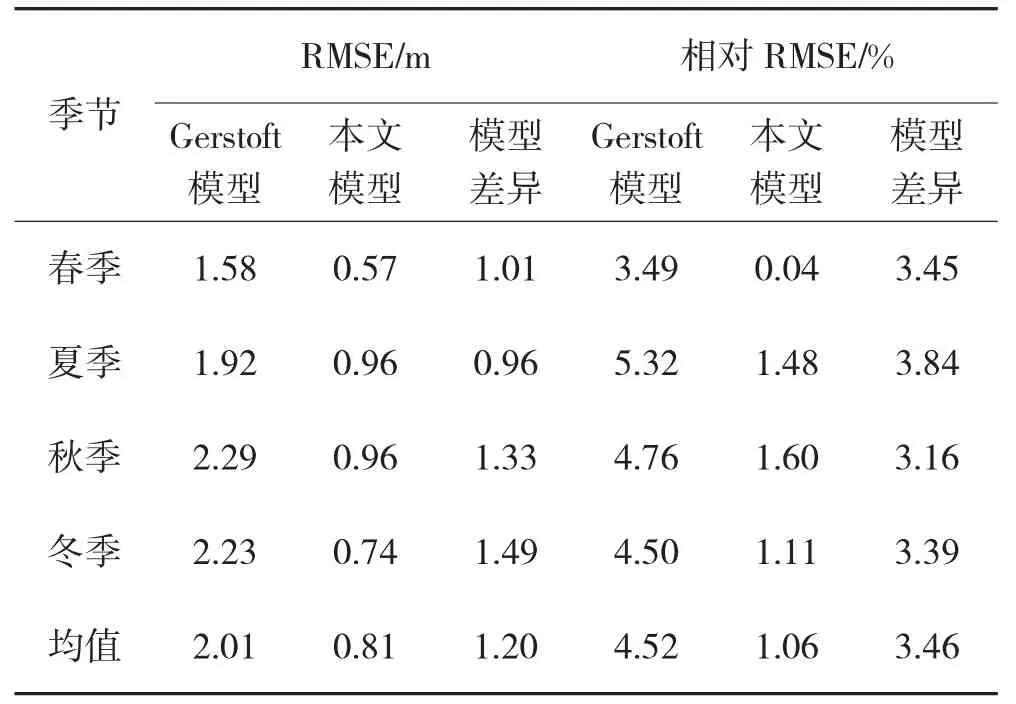
表2 Gerstoft 模型与本文模型的RMSE 对比Table 2 The comparison of RMSE between the Gerstoft model and the proposed model

1）根据全年平均值对比的情况,本文模型较Gerstoft 模型在四季预测蒸发波导高度均方根误差（RMSE）更小.

2）根据全年平均值对比的情况,本文模型较Gerstoft 模型在四季预测蒸发波导高度相对均方根误差（RRMSE）误差更小.

3）模型差异对比发现,本文模型预测结果较Gerstoft 模型有显著的提高.全年平均均方根误差（RMSE）降低了1.20 m,全年平均相对均方根误差（RRMSE）降低了3.46%.

4）通过图表各项指标对比发现,本模型的蒸发波导预测精度在该海域均优于Gerstoft 多参数模型.这说明统计机器学习的方法是研究蒸发波导预测模型的有效工具.

4 结论

本文利用机器学习方法建立了一种蒸发波导智能化预测模型,实验证明该模型的预测结果与输入数据吻合较好.通过与实测结果的对比,本文模型的预测精度比Gerstoft 多参数模型预测结果更加精确,平均提升量为3.46%.

本研究旨在为蒸发波导特性预测模型的研究提供一种新途径,进而为海上无线电系统规划设计、作战指挥控制提供技术支撑.该模型仅需要导入该地区不同高度下的实测修正大气折射率,即可反演出适合该区域的参数,并进一步得出该区域的修正大气折射率剖面,从而对该区域蒸发波导的高度进行预测.预计未来的研究会将重建模型的适用性扩展到更广泛的地区乃至全球,实现使用该模型重建方法在时间和空间上对全球蒸发波导高度的预测,以支撑无线信道及其效应评估,进而为有效掌握和应用海上作战环境、支撑系统规划设计、占领电磁环境与频谱战优势提供技术基础.