基于优劣解距离算法的光储配电网自适应虚拟惯性控制策略

余 威， 杨欢红， 焦 伟， 周 泽

(上海电力大学 电气工程学院， 上海 200090)

随着可再生能源在配电侧渗透率的不断增高和电力电子技术的飞速发展，光伏兼具清洁无污染和维护成本低的优势，仍具备较大的开发利用价值[1].但光伏出力不稳定，需与储能模块灵活配合，才能保证电力系统供电可靠性.目前光储单元大部分经过电力电子设备接入电网，变流器的物理隔离作用导致系统的机械惯性不足，电网中存在扰动时，无法像同步发电机一样为系统提供惯性功率[2].因此，如何采取新的手段来实现光储配电网惯性调控的灵活性，从而提高协同控制效率成为亟待解决的课题.

将虚拟同步发电机控制策略引入电力系统需求侧调频，可以在换流器中模拟出发电机特性，提升系统抗扰动能力[3].文献[4]将虚拟同步发电机应用于微电网，实现并网和离网灵活转换.文献[5]对虚拟惯量恒定(Virtual Synchronous Generator，VSG)展开深入研究，并对其进行完善，结合系统变化状况能够快速且准确地调节惯性时间常数值，增强系统稳定性.文献[6]对各单元虚拟惯量进行研究，发现频率不同时，电源提供的动态支撑功率随之变化.文献[7]在有功频率控制过程中对同步发电机展开了更深入的研究，认为虚拟同步发电机的控制方法与系统的频率变化率有关，当频率变化率发生改变时，控制方式也应对应做出调整.此外，文献[8]还提出了灵活虚拟同步发电机控制策略，认为最佳阻尼比是影响VSG系统振荡的一个重要因素，在对此假设做出论证后作者还研究出了对应的控制策略，有效改善了系统动态指标数值，并提升了动态稳定性.文献[9]研究了VSG频率自恢复控制方法，能较高效地控制频率波动，让其在最短时间内恢复到稳态，且不会因复杂通信系统而波动.文献[10]提出一种自适应惯性的VSG控制策略，通过参数的连续平滑调节，抑制并网逆变器输出功率和输出频率的波动.文献[11]在超级电容器侧应用VSG控制，设计准同期控制单元，消除相位差对并离网切换的影响.上述文献未考虑换流器参数及多光储单元运行情况对控制策略的影响，为了改善系统动态响应能力，在研究过程中会借助VSG中虚拟惯量的灵活可调性.虽能在一定程度上达到控制目标，但也存在不稳定性，主要在于没有充分考虑到虚拟惯性灵活调节受到多种条件的约束，例如瞬间释放功率、换流器的容量限制等.因此，需充分考虑这些因素带来的影响.

灵活虚拟同步发电机所具备的虚拟惯性灵活可控，当系统中的频率发生变化时，虚拟惯性随之进行动态响应，存在功率扰动的情况时，系统的频率仍会保持稳定[12].并且随着多光储单元场景应用的增加，需全面考虑协同控制时各单元参数带来的影响.本文提出一种基于优劣解距离算法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)的光储配电网自适应虚拟惯性控制策略，以多指标评价体系为基础，对VSG单元的虚拟惯量协同分配进行更深入的研究，优化系统动态响应能力，提升电网侧的频率质量，最后通过算例仿真验证所提控制策略的有效性与优越性.

1 光储单元的灵活虚拟惯性控制

1.1 模型的建立

考虑电力系统拓扑结构复杂性及多光储单元接入电网形式多样性，本文重点研究包含混合光储单元的六端系统，如图1所示.储能装置包括超级电容器(SC)和蓄电池(BAT)，共包含3个光储单元，VSG1和VSG2单元相同，VSG3单元由光伏模块和超级电容器组成.G1和G2为传统的发电机组，G1向系统提供恒定功率，G2负责系统的动态响应，即发生扰动时，补充功率缺额，保持频率稳定； PV为光伏模块.

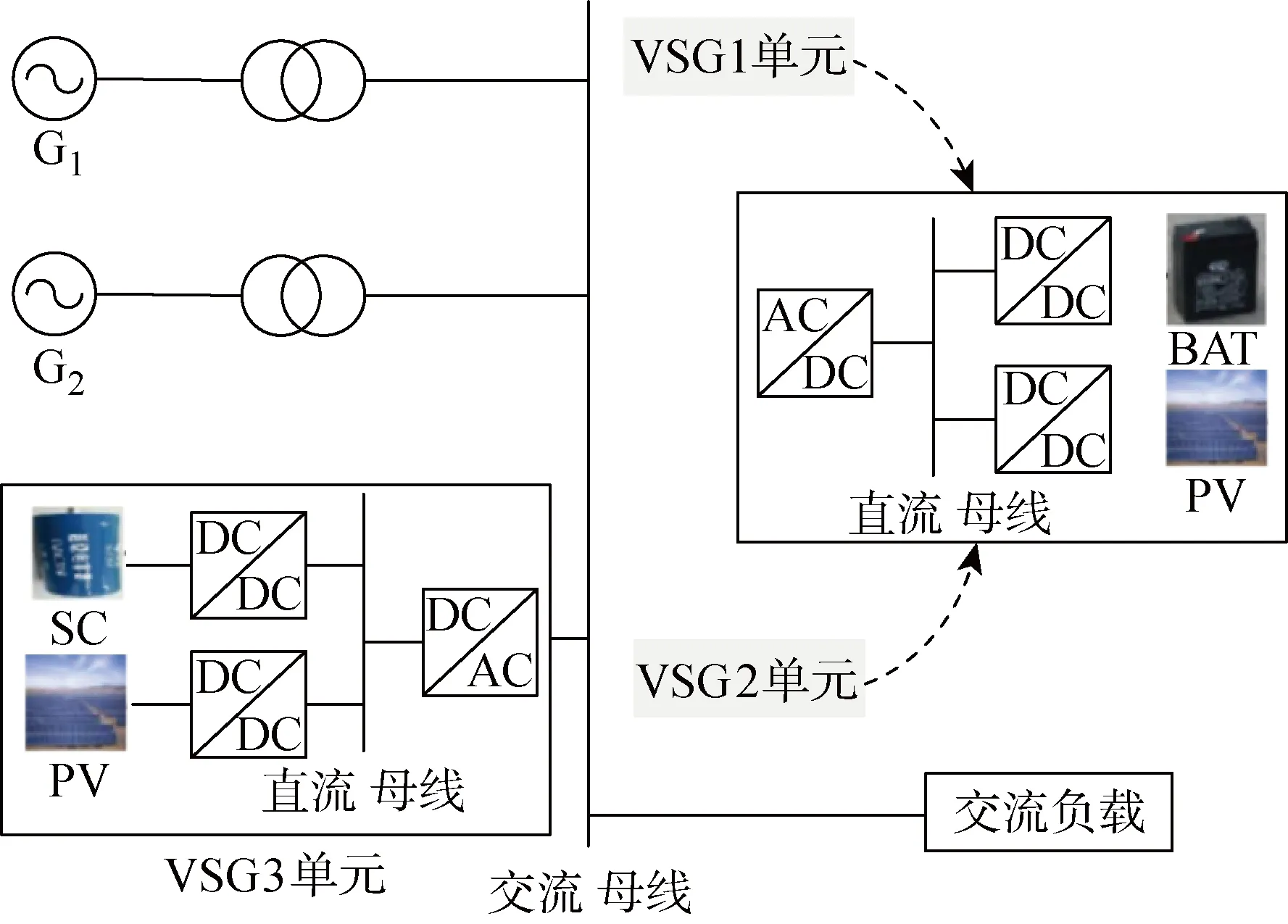
图1 含混合储能的六端系统拓扑Fig.1 Six terminal system topology with hybrid energy storage

1.2 灵活虚拟同步发电机控制策略

根据转子运动方程，引入系统频率变化率，并结合比例函数与指数函数得到灵活虚拟同步发电机控制(Flexible Virtual Synchronous Generator, FVSG)策略：

(1)

式中：H为虚拟惯量；H0为虚拟惯量初始值；f为电网侧频率；t为响应时间；M为所设定的阈值；ke、kf为虚拟惯量的的比例系数及指数系数.由式(1)可知，H取值与系统频率变化率有关，理论分析得到暂态情况下系统频率变化率越大，虚拟惯量取值越大，此时对频率波动的抑制效果越好，有利于改善系统电能质量，并且频率变化率小于设定阈值时，为一固定值，避免了频繁的切换；频率变化率大于设定阈值时，随着频率的变化率进行灵活变换，变流器为系统提供惯性功率支撑，维持系统频率稳定，提高电能质量.ke、kf在频率变化率的基础上对虚拟惯量的大小进行进一步调整，其取值需兼顾虚拟惯量的大小和对系统稳定性的影响.系统正常运行时频率值比较稳定，频率变化率很小，此时系统的虚拟惯量保持恒定为H0，避免了在正常运行时虚拟惯量的频繁切换对系统的稳定运行带来冲击，本文研究依据文献[13]ke、kf分别取25, 0.5.

图2所示为对应控制框图，图中：Pref为系统有功功率参考值；Po为光储单元输出功率；Kd为阻尼系数；ωg为系统角频率；ω为光储单元角频率；1/s为积分环节.

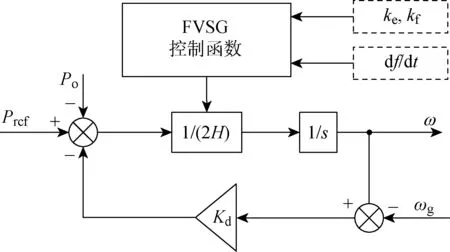
图2 FVSG控制框图Fig.2 Block diagram of FVSG control

1.2.1考虑荷电量影响 上述控制策略引入系统频率变化率进行惯性支撑，光储单元自身参数及性能也会对虚拟惯性的提供产生影响，例如蓄电池充放电极限、频率变化率、系统单位时间功率允许波动量等.蓄电池具体充放电情况为

(2)

式中：SSOC为蓄电池荷电状态；a为蓄电池放电时的极限值；b为蓄电池充电时的极限值.根据荷电状态进行控制，当蓄电池处于极限情况下，无法正常工作，仅考虑SOC与虚拟惯量H之间的关系即可.稳态运行时，有功功率、角频率以及虚拟惯量之间的关系如下：

(3)

式中：Pin为光储单元输出有功功率给定值； ΔP为有功功率的变化量.当蓄电池在充放电极限状态时，希望P尽量小，角频率变化量在短时间内的变化较小，忽略不计，荷电量影响下H的表达式为

(4)

式中：k1、k2为虚拟惯量相关系数.若蓄电池荷电量处于极限状态，H的值会不断减少，这主要是因为反正切函数在发挥作用.当H变小后，有功变化量ΔP也会相应变小，蓄电池减少出力，本文所提控制策略摆脱了固定惯量的弊端.

1.2.2非荷电量影响 在控制过程中，系统频率变化率、换流器容量以及系统单位时间功率可调量等因素十分关键.H值应控制在较小的范围内，此时系统内部的功率变化量就会减小，换流器的负担也会相应减轻.此外，如果VSG系统单位时间内有功变化量较大，那么也应该将H的值控制在较小的范围内，从而保证系统功率变化率在稳定运行范围内.由此可知，如果蓄电池处于正常工作状态时，虚拟惯量H的表达式为

H=η1Hf+η2HC+η3HP+H0

a≤SSOC≤b

(5)

式中：η1、η2、η3为光储单元影响参数的权重系数，3者之间的总和为1，其中的某一个值越大，意味着该影响因素所对应的权重系数越大；Hf、HC、HP为3个不同的虚拟惯量，它们分别受不同因素影响，其中Hf受频率变化率影响，HC受换流器容量影响，HP受系统单位时间功率可调量影响；k3～k8为虚拟同步发电机控制的相关系数；C1为换流器瞬时交换功率；CN为换流器额定容量；ΔPt为单位时间功率变化量；ΔPtmax为单位时间功率可调量.由式(5)可知，系统频率变化率增大时，H增大；电力电子换流器交换功率增大时，H减小；系统单位时间功率变化量增大时，H减小，该数值变化符合系统运行时的实际情况.在非SOC影响的情况下，如果换流器处在极限运行的状态，为了保证系统的稳定运行，可以对H进行调整.

蓄电池稳定运行，着重分析系统频率变化率、换流器容量以及系统单位时间内功率可调量对蓄电池的作用.由于换流器瞬时交换功率增大，临近额定容量时，H取较小值，功率变化量随之变小，换流器的出力减少.VSG单位时间内有功变化量增大，H随之变小，功率变化量也会减小，保证系统功率在允许范围内波动.综上所述，可以得知虚拟惯量控制策略受多个因素影响：

(6)

式中：H1、H2、H3分别为光储单元VSG1～VSG3向系统提供的虚拟惯量.如果蓄电池处于稳定运行状态，那么可以通过分析其余因素来得出H的数值.蓄电池如果处于极限运行状态，所提控制策略就会受反正切函数影响，则H变小，P也变小，蓄电池出力减少，且过充和过放现象更明显，H降低越快，控制作用就更加明显.所提控制策略可根据实际情况灵活调整H，从而达到改善蓄电池工作情况的作用.

2 多光储单元系统的协同运行

2.1 扰动下协同控制策略

从响应速度方面，超级电容器的效果较为理想，当系统内部存在高频扰动时，由超级电容器向系统提供惯性功率支撑，但是超级电容的能量密度较小，因此储存能量效果并不突出.当超级电容的容量被耗尽时，需用蓄电池向系统供能，提高动态响应稳定性.在高频干扰下，为了由超级电容实现惯性支持，并维持蓄电池输出功率不变，对各VSG单元的虚拟惯量进行合理分配，以保持有功出力恒定.

(7)

式中：λ为一固定值.

超级电容受其体积和能量密度的影响，储存电能容量有限，超出容量范围时，继续使用会影响其使用寿命及电能质量，因此系统频率变化率较大时，需对上述控制策略进行改进.当高频扰动为正，在能量储备供给惯性以补偿能量缺口时，需减小VSG3单位的虚拟惯量，用蓄电池来抑制高频干扰；若系统中的功率扰动为负值，需减小各单元输出功率，减小VSG3单元出力，保证超级电容两端电压在给定范围内，以延长其寿命，改进后控制策略如下.

dP/dt≥0时，

(8)

dP/dt<0时，

(9)

式中：δSOCl为第l个VSG单元中储能模块的实际荷电状态.

2.2 基于TOPSIS算法的多光储单元协同控制

针对储能装置为蓄电池的多光储单元协同控制，对光储单元的结构进行分析研究，得到影响光储单元运行的主要因素如下：蓄电池荷电量δSOC、蓄电池允许功率波动范围ΔPtBAT、电力电子换流器允许功率波动范围ΔPN、系统单位时间内允许功率波动范围ΔPtmax.首先根据各VSG单元中蓄电池的总剩余能量对系统的总惯量进行调整，含蓄电池的多光储单元总虚拟惯量为

HT=αke|df/dt|k2

(10)

式中：α为调整系数，确保根据光储单元的容量进行惯性功率支撑.

引入优劣解距离法，又称逼近于理想值排序算法，找到最佳虚拟惯性功率分配方案，将各光储单元为系统提供惯性功率设定为一分配方案，系统中所有的光储单元构成方案集，配合蓄电池的影响指标，构成评估矩阵：

(11)

各光储单元构成方案集A，A={a1,a2,a3}；δSOC、ΔPtBAT、ΔPN、ΔPtmax构成属性向量；评估矩阵中元素，如x12，表示第1个光储单元在第2个影响因素中的评分.

制作加权规范矩阵，确定各属性达到最好值的方案，即最优解Z*，以及各属性为最坏值的方案，即最劣解Z0，算出所求距离，其中第i个惯性支撑方案到最优解的最近距离及最劣解的最远距离：

(12)

(13)

然后计算各方案的虚拟惯性功率分配比：

(14)

最终得到协同控制下各个光储单元的虚拟惯性系数：

(15)

式中：Hl为经TOPSIS算法评估后第l个VSG单元向系统提供的虚拟惯量.

图3所示为引入TOPSIS算法后的多光储单元协同控制流程图，图中：fN为系统额定频率，一般取50 Hz；ΔPtBATl为第l个光储单元的蓄电池允许功率波动范围；ΔPNl为第l个光储单元的电力电子换流器允许功率波动范围；ΔPtmaxl第l个光储单元的系统单位时间内允许功率波动范围.首先根据系统变化率确定系统虚拟惯量系数，得到各光储单元向系统提供的总虚拟惯量；然后引入TOPSIS算法，根据影响蓄电池运行的4个影响因素，确定指标体系，构造评估矩阵，求出最优解和最劣解；最后根据各方案到最优解和最劣解的距离，确定方案的最终排序，得到最优的功率分配策略.

图3 多VSG单元协同控制流程图Fig.3 Flow chart of multi-VSG unit cooperative control

3 仿真分析

3.1 协同控制策略验证

为深入探究所提协同控制策略的可行性，在RT-LAB硬件(OP5600仿真机)搭建测试平台，结构框图如图4所示.将所提控制策略应用于数字信号处理器(Digital Signal Proces, DSP)中，并与负荷控制器、微源控制器及功率转换系统相连接，产生的脉冲宽度调制(Pulse-Width Modulati, PWM)连接信号输入端.本研究中，光照强度均取 1 000 W/m2，储能装置额定电压为310 V，各光储单元虚拟惯量H均取1.5.

图4 测试平台设计框图Fig.4 Block diagram of test platform design

高频扰动出现后，对超级电容器容量充足时所提协同控制进行试验验证.运行初期，系统稳定工作，在系统运行5 s后，增加3 kW负载至系统交流侧，试验当中各VSG单元惯性参数和有功出力变化如图5、6所示.

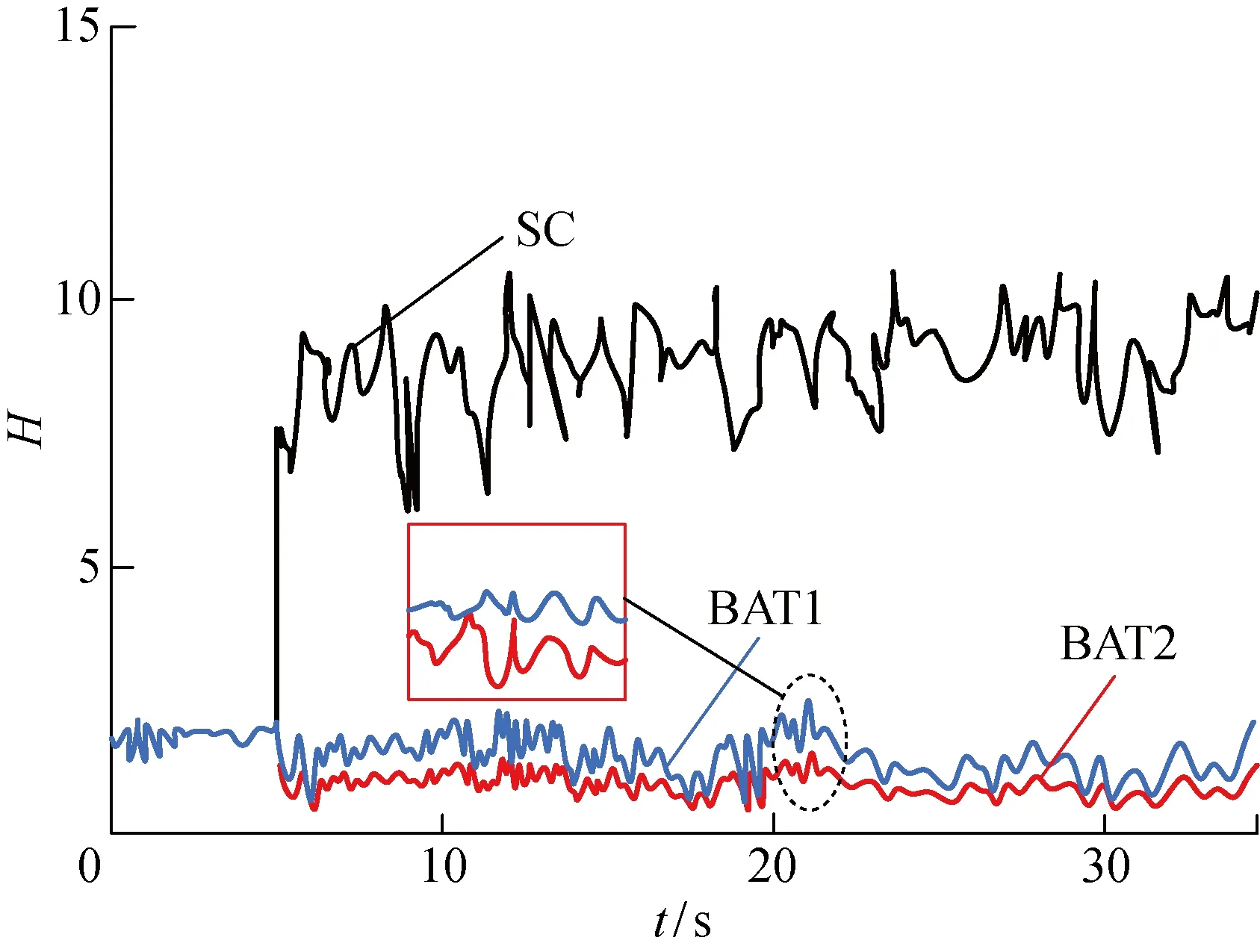
图5 高频扰动下惯性系数变化Fig.5 Variation curves of inertia coefficient in high frequency control

图6 高频扰动下有功出力变化Fig.6 Variation curves of active output in high frequency control

由图5、6可知，初始状态各光储单元虚拟惯量大小相等，均为设定值1.5.系统增加负载后，对频率造成扰动，此时由超级电容优先调整出力，向系统提供功率缺额，储能装置为蓄电池的光储单元出力基本不变，减少其充放电次数，延长使用寿命.图5、6说明在暂态情况下，各光储单元应用所提控制策略后，超级电容可以快速响应，提供支撑功率，同时也达到减小蓄电池充放电次数的目的.

图7、8分别为协同出力下各端惯性系数以及有功出力.当超级电容两端电压不在给定范围时，即电能储存容量较低时，需与含蓄电池的光储单元协同出力.由图7可知，同样在初期给系统增加3 kW交流负载，各光储单元虚拟惯性初始值均为1.5，此时超级电容两端虚拟惯量大小基本不变，主要由蓄电池向系统提供功率缺额，减小超级电容端供电压力，并且由于蓄电池性能参数不同，提供的虚拟惯性功率大小也不同.图7、8表明，协同控制可以根据蓄电池的荷电状态实现各储能装置的有功出力合理分配，储备效果更好，系统更加稳定.

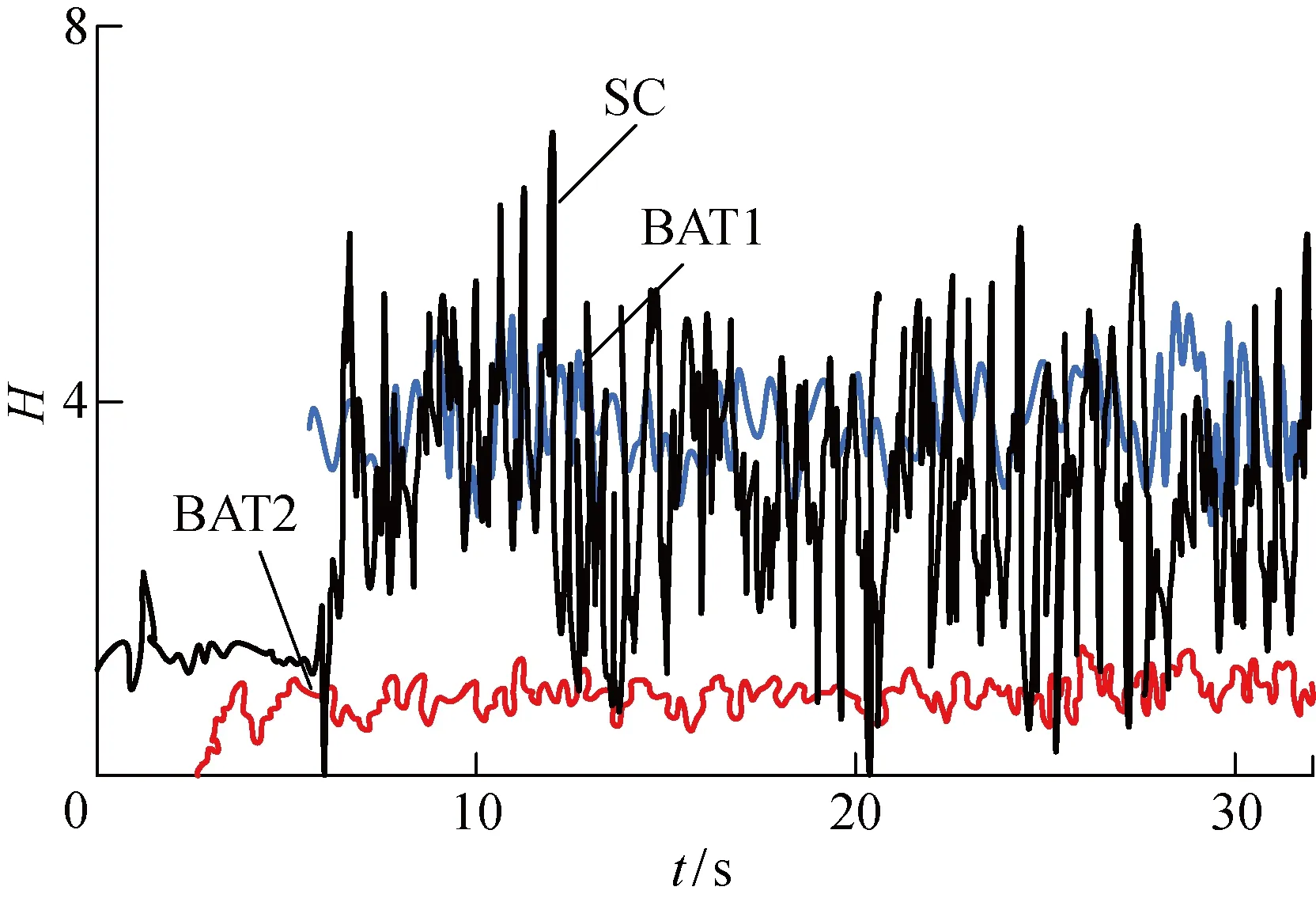
图7 协同出力下各端惯性系数Fig.7 Inertia coefficient of each end in coordinated force

图8 协同出力下各端有功出力Fig.8 Active output of each end under coordinated output

3.2 多指标影响下优化效果

利用引入优劣距离算法后的协同控制策略，对惯性支撑能力进行合理分配.采用控制变量法，将3个光储单元的荷电状态、蓄电池允许功率波动范围、系统单位时间内允许功率波动范围保持一致，改变换流器额定功率，分别取2、4、6 kW，系统稳定运行一段时间后，增加4.5 kW交流负载，观察各端参数变化情况.图9所示为额定功率不同时各端惯量和有功输出变化，图中Pol(l表示曲线1, 2, 3)代表各光储单元输出功率，负载增加后，系统功率缺额增大，各光储单元向系统提供不同大小的虚拟惯性功率.可知，电力电子换流器的额定功率越大，供电可靠性越高，提供的惯性功率越多；额定容量越小，提供的惯性功率越少，保证小容量的光储单元在安全运行范围内运行，同时又能增加系统动态响应能力，具有较强的实用性.

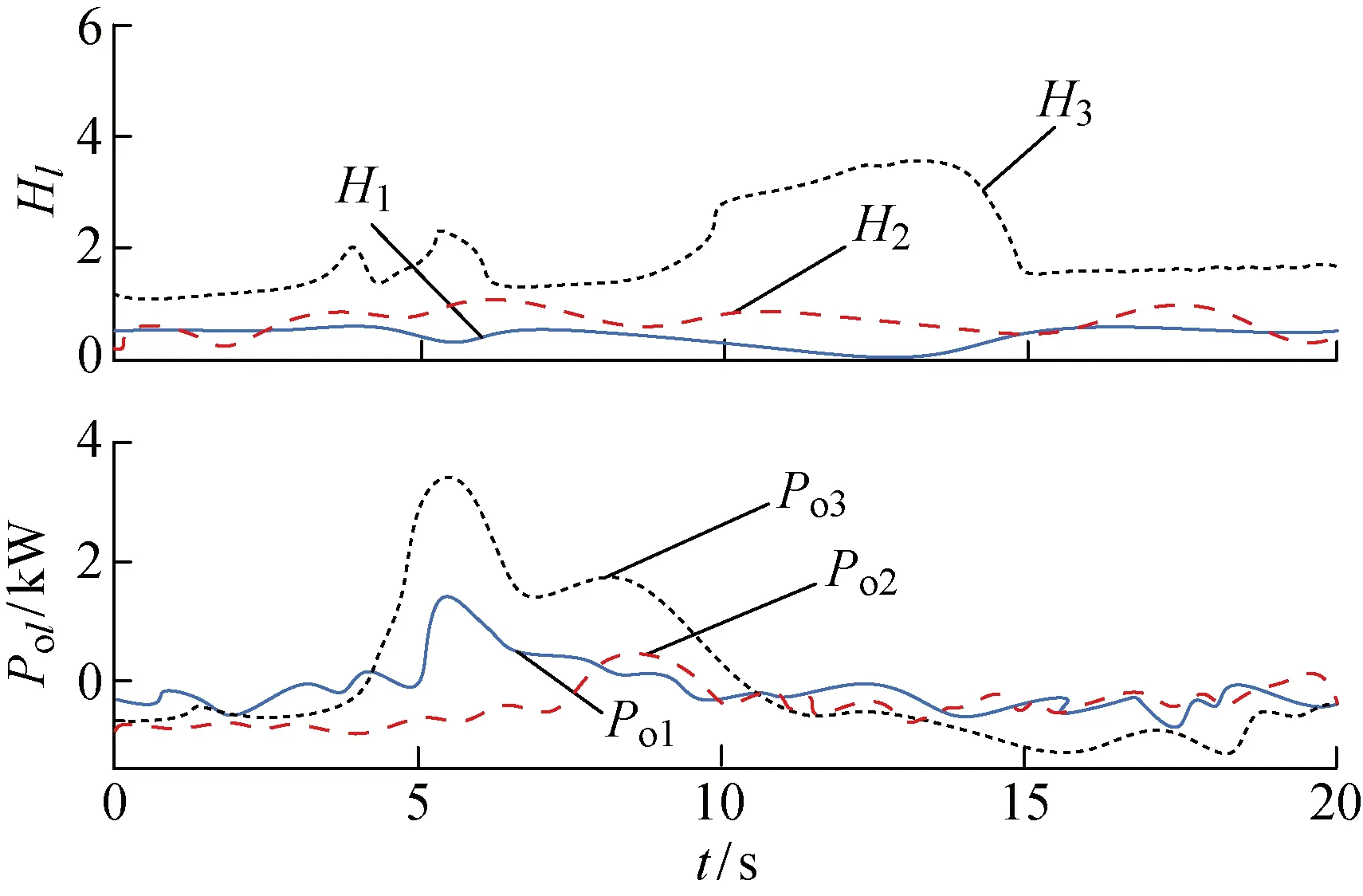
图9 额定功率不同时各端惯量和有功输出变化Fig.9 Change of inertia and active power output of terminals at different values of rated capacity

当各评价指标存在差异时，取其差异最大的评价指标作为根据进行虚拟惯性功率的分配，对其进行试验验证，各VSG单元参数如表1所示，蓄电池荷电量及换流器额定功率不同，其余评价指标均相同，在系统运行5 s后，系统有功负荷减少5 kW.暂态初期，各VSG单元可用容量均较多，此时以蓄电池的荷电量作为主要评价指标，随着各单元向系统提供有功功率，各VSG单元可用容量出现差异，此时以换流器容量作为主要评价指标.由表1可知，光储单元VSG1的数值最差，所提控制策略开始减小其向系统提供的虚拟惯性功率，防止其出现过度放电的情况.

表1 VSG单元参数设定Tab.1 VSG unit parameter setting

图10所示为多指标差异时各端惯量和有功输出变化.图10表明，所提控制策略可以凭借各个评价指标的实时差异进行虚拟惯性功率的分配，保证系统的安全稳定运行.

图10 多指标差异时各端惯量和有功输出变化Fig.10 Change of inertia and active power output of terminals with difference of multiple indicators

4 结论

针对多光储VSG单元的协同运行问题进行了研究，搭建了含混合储能装置的六端交流电网模型，通过理论研究和仿真分析得出如下结论：

(1) 提出一种多VSG单元协同控制方法，系统发生扰动时，初期由响应速度较快的超级电容提供功率支撑；容量不足时，蓄电池与其协同出力，考虑荷电量及非荷电量影响下的控制策略，以改善蓄电池运行工况.

(2) 为了更加深入地进行多指标综合评价下多光储单元之间的协同控制研究，引入优劣距离算法，选取换流器允许功率波动范围、储能装置允许功率波动范围等因素作为协同控制的评价指标，根据评价指标的优劣程度，对各VSG单元的惯性支撑能力进行准确评估，为功率分配提供参考.

(3) 根据六端交流系统的拓扑结构，搭建硬件在环试验平台，经过试验证明控制策略的可靠性，并通过仿真试验证明了该方法能够根据不同的运行特性，实现不同的功率输出，并优化储能储备.在功率扰动的情况下，各储能装置在不影响电能质量的前提下，系统可提高系统动态响应能力.