含瓦斯煤岩流变规律及三维本构模型研究
(华北科技学院 应急技术与管理学院,北京 101601)
煤与瓦斯突出是煤矿井下采掘过程中发生的一种极其复杂的地质动力现象,可在短时间内由煤体向采掘空间抛出大量煤炭及涌出大量瓦斯,并造成一定的动力效应。随着我国煤炭资源进入深部开采,煤与瓦斯突出的危险性进一步增加,众多学者采用各种试验及现场研究方法,对煤与瓦斯的突出机理进行了广泛的研究,并取得了一定的成果,但对突出的机理还没有形成统一的见解,仍停留在各种假说的基础上。由于煤与瓦斯突出机理本身的复杂性,各种突出机理假说对突出过程中的巨大动力效应、复杂的突出过程及突出过程中瓦斯的理化效应等方面还不能作出很好的解释,很大程度上影响了对煤与瓦斯突出的有效防治。煤与瓦斯突出,特别是延期突出与含瓦斯煤岩流变性质密切相关。
长期以来,众多学者对于含瓦斯煤的力学性质以及力学模型的构建进行了大量研究。周世宁等[1]在综合作用假说的基础上首次提出“流变假说”,并初步建立起含瓦斯煤蠕变行为的数学模型;王家臣等[2]通过型煤加、卸载试验研究,发现瓦斯对煤样力学性质的影响随围压的增大而减小;李祥春等[3]发现随着瓦斯压力的增大,煤岩的蠕变变形增大,提出蠕变拐点的观点;陆占金等[4]通过型煤试件渗透率与体积应变试验,发现随着瓦斯压力的增加,煤样的峰值强度呈减小趋势;蒋长宝等[5]研究发现随着含水率增加,煤样变形量和破坏程度增大。以上研究侧重于通过室内试验定性得出含瓦斯煤岩的相关力学性质。基于上述研究内容,大量学者开始构建含瓦斯煤体相关模型实现对含瓦斯煤体的定量化描述:鲜学福等[6-7]得到了含瓦斯状态下的煤岩蠕变状态方程,并构建了含瓦斯煤固-气耦合数学分析模型;蒋长宝等[8-12]对含瓦斯煤岩进行研究,建立了含瓦斯煤岩的固气耦合模型,并利用有限元方法得出该模型在定解条件和相关参数下的数值解;魏建平等[13]利用表面化学与有效应力理论,构建了不同因素影响下的含瓦斯煤体渗透率动态演化模型。随着含瓦斯煤体相关模型的建立,部分学者开始运用数值模拟对其进行更加深入的研究:刘力源等[14]通过引入双重损伤本构关系构建了膨胀应力耦合分析模型,同时通过数值模拟结果与试验结果的对比验证得出饱和CO2压力越大诱发的煤损伤越大的结论;武文宾[15]通过研究煤岩体孔隙度动态变化,形成了水压致裂的应力-渗流耦合模型和水压致裂煤体失效判据,并通过数值模拟预测结果验证了模型的可靠性;郝建峰等[16]构建了含瓦斯煤体的热-流-固耦合模型,并以此为基础进行了煤与瓦斯相互作用机理数值模拟。
在前人研究的基础上,基于含瓦斯煤岩三轴流变试验结果,分析含瓦斯煤岩的流变行为,并依据有效应力和流动法则建立含瓦斯煤岩三维蠕变本构方程,同时验证其合理性,研究成果对于丰富含瓦斯煤岩流变力学理论具有重要的现实意义。

图1 RRTS-Ⅳ型岩石流变扰动效应试验主机Fig. 1 RRTS-Ⅳ rock rheological disturbance effect test host
1 试验概况
1.1 试件制备
切割大块原煤,打磨制成直径50 mm、高度100 mm的圆柱型试件,经声波探测后选取测量结果相近的试件进行试验。
1.2 试验系统
采用自主研发的RRTS-IV型岩石流变扰动效应试验机和含瓦斯煤岩流变扰动渗流试验装置。其中RRTS-IV型岩石流变扰动效应试验机主要由试验主机以及动态数据采集系统组成,试验主机如图1所示,含瓦斯煤岩流变扰动效应渗流试验装置如图2所示。
1.3 试验方案
试验选取两组煤样,每组煤样选取5块,分别编号A-1~A-5以及B-1~B-5。
A组煤样在试验过程中围压均设定为2 MPa,A-1~A-5试件均通入瓦斯,吸附瓦斯时间24 h,并使瓦斯压力值分别保持在预设值0.1、0.5、1、1.5和1.8 MPa。
B组煤样在试验过程中瓦斯压力设定为1 MPa,瓦斯吸附时间同样为24 h,B-1~B-5试件围压值分别设定为1.2、1.5、2.0、2.5和3.0 MPa。
含瓦斯煤岩流变扰动效应渗流实验装置通过自动补卸压能够保持试样围压及瓦斯压力的长期稳定,补偿误差为±0.1 MPa。

图2 含瓦斯煤岩流变扰动效应渗流试验装置Fig. 2 Seepage experimental device for rheological disturbance effect of gas-containing coal rock
两组煤样均采用分级加载的方法,从轴压4 MPa开始加载,加载等级为4 MPa,每级加载待流变稳定后再进行下一级加载,且加载时间保持相同。整个试验过程中记录轴向应变数据。
1.4 试验结果
表1和表2分别为两组煤岩试件的试验结果,图3和图4分别为试件A-5和试件B-5在各级荷载下的试验曲线。
1) 由表1结果可知,在相同围压和轴向压力作用下,瓦斯压力越大,轴向变形越大,且处于稳定蠕变阶段的煤岩变形随瓦斯压力增大呈明显的阶梯性增长。
2) 由表2结果可知,在相同瓦斯压力和轴向压力作用下,围压越大,轴向变形越小,且随围压增大,处于稳定蠕变阶段的煤岩应变不断减小。
3) 由图3和图4可以看出,当最后一级荷载加上去后,试件应变(ε)在短时间内急剧增大并发生破坏,由此推断发生不稳定蠕变的含瓦斯煤岩处于加速蠕变阶段的时间很短,其余发生变形的绝大部分时间都处于稳定蠕变阶段。

表1 A组煤样试验结果Tab. 1 Experimental results of group A coal samples

表2 B组煤样试验结果Tab. 2 Experimental results of group B coal samples
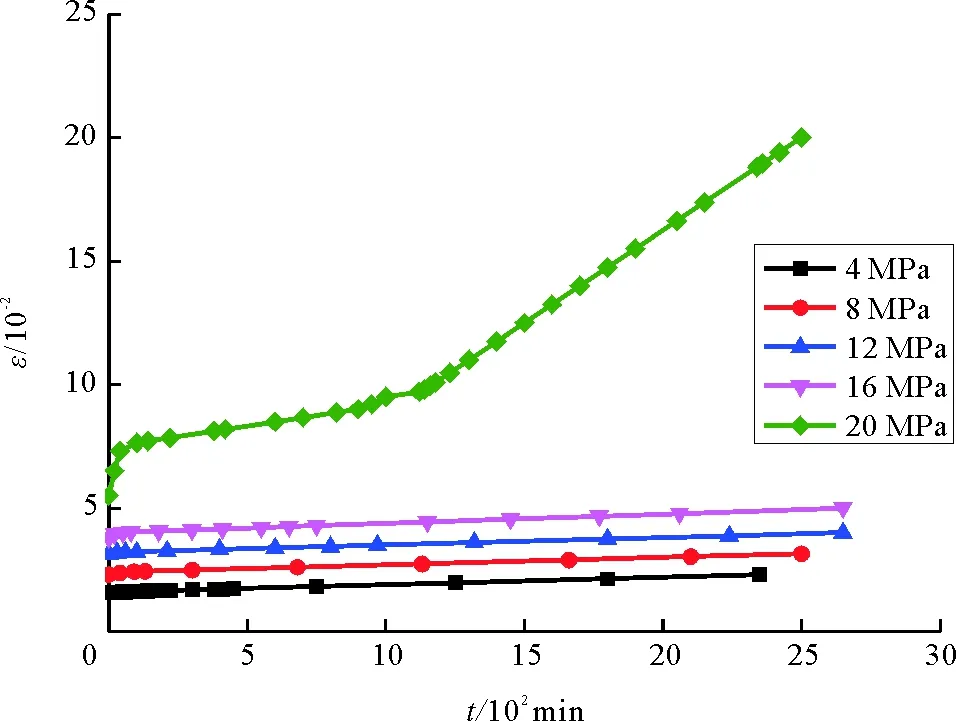
图3 试件A-5试验曲线Fig. 3 Experimental curve of specimen A-5

图4 试件B-5试验流变曲线Fig. 4 Experimental rheological curves of specimen B-5
2 本构方程建立与参数分析

图5 西原体模型Fig. 5 Nishihara model
2.1 西原模型
为建立三维应力状态下的蠕变本构方程,首先建立一维状态下的蠕变本构方程。在一维应力状态下,最能反映蠕变三阶段的模型为西原体模型。西原体模型由胡克体、开尔文体和理想黏弹塑性体串联而成,如图5所示。其中:k1、k2—一维弹性系数;η1、η2—一维黏性系数;σs—屈服应力;σ—模型所承受外压力。西原体的蠕变方程为:
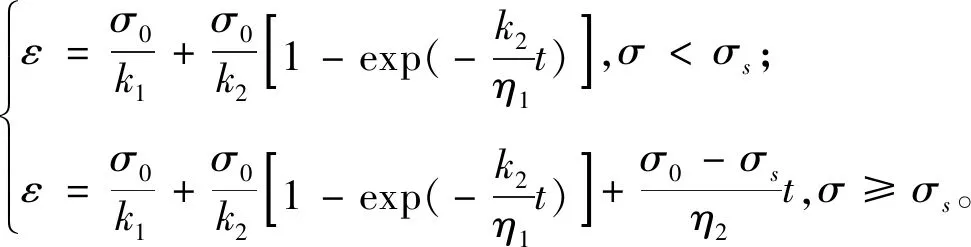
(1)
2.2 含瓦斯煤岩三维蠕变本构方程的建立
由于含瓦斯煤岩的应力与蠕变速率之间的关系并不是简单的线性关系,且应力状态十分复杂,建立蠕变本构方程时做如下假设:①正应力的主方向与变形的主方向相同;②煤岩内部力学性质为各向同性,且变形前后体积不发生变化;③主切应力与滑移变形速度成正比;④切应力的大小始终保持一致。
考虑有效应力原理:
(2)

同时,为了确定在加载过程中含瓦斯煤岩产生的塑性应变的增量,引入流动法则:
(3)

由式(1)和(3)可以得到:

(4)
考虑到t=0时,
(5)
同时,对式(4)中时间t进行一次积分,可以得到式(6):

(6)
式中:G=E/(2+2ν);E1、E2—弹性系数为k1、k2的弹性体弹性模量;H1、H2—三维黏性系数;ν—泊松比;σs—屈服应力;σ—三维有效应力;δij—Kronecker符号。
式(6)是初步建立起的含瓦斯煤岩三维蠕变本构方程。为了确定最大主应力方向的应变,令σ11=σ1,σ22=σ33=σ3,ν取0.5,同时考虑变形开始加速的时间为tα,则最大主应力σ1方向的主应变S1为:
(7)
式(7)为修正后的含瓦斯煤岩三维蠕变本构方程。式中:tα—变形开始加速的时间;t0—单位时间;K—待定系数;σ1-σ3—主有效应力。
2.3 蠕变本构方程的验证与参数分析
2.2节中得到修正后的含瓦斯煤岩蠕变本构方程,选取试件A-5的试验结果验证模型的合理性,首先利用MATLAB得出拟合曲线,然后将拟合曲线与试验得出的曲线进行对比,表3为试件A-5回归反分析各参量值结果,图6为试件A-5的拟合曲线与试验曲线对比结果。

表3 试件A-5三维蠕变模型回归反分析结果Tab. 3 Regression back analysis results of specimen A-5 three-dimensional creep model
利用线性回归分析得到两组煤样拟合曲线与试验曲线的线性回归相关系数,A-5在各级荷载下的回归相关系数分别为0.98、0.97、0.97、0.98和0.99,线性回归相关系数均大于0.97。通过图6可知,拟合曲线与试验曲线的吻合度较高,表明所建立的含瓦斯煤岩三维蠕变本构方程是可靠的。
通过表3可知,在tα之前,煤岩变形速率并未增大,在tα之后,煤岩变形速率开始急剧增大。由此推断煤岩发生破坏时存在一时间节点tα,在tα之前,煤岩变形速率不会发生明显增大,呈现稳定蠕变的特征;而tα之后,煤岩在短时间内发生急剧破坏,变形速率明显增大,呈现出不稳定蠕变的特征。
相关理论认为含瓦斯煤岩的破坏与内部有效应力有很大关系,且变形主要由主方向的主应力来控制,结合表3得出的含瓦斯煤岩蠕变本构方程中各主要参量值与主有效应力之间的关系,如图7所示。

图6 试件A-5在各级荷载下的实验曲线与拟合曲线对比Fig. 6 Comparison of experimental curves and fitting curves of specimen A-5 under different loads
通过图7可以看出,随荷载等级增加,主有效应力(σ1-σ3)一直在增大,E1、E2和H1值则随主有效应力(σ1-σ3)的增大呈现先增大后减小的规律。在达到屈服点之前,随着荷载增加,煤岩逐渐被压密实,内部孔隙逐渐闭合,各成分逐渐黏合在一起,E1、E2和H1值逐渐增大;当超过屈服点之后,由于煤样开始发生破坏,内部出现新的裂隙,并且随着时间推移内部裂隙不断扩展,煤岩内部各组分的黏合性变差,煤岩强度变低,E1、E2和H1值随之减小。其余试件流变规律与试件A-5类似,且拟合结果与试验结果保持一致。
通过建立的含瓦斯煤岩三维蠕变本构方程推断出含瓦斯煤岩存在极限变形量,结合试验过程可知,当含瓦斯煤岩的变形量达到该值时,应变速率会在短时间内急剧增大,导致煤岩发生破坏。
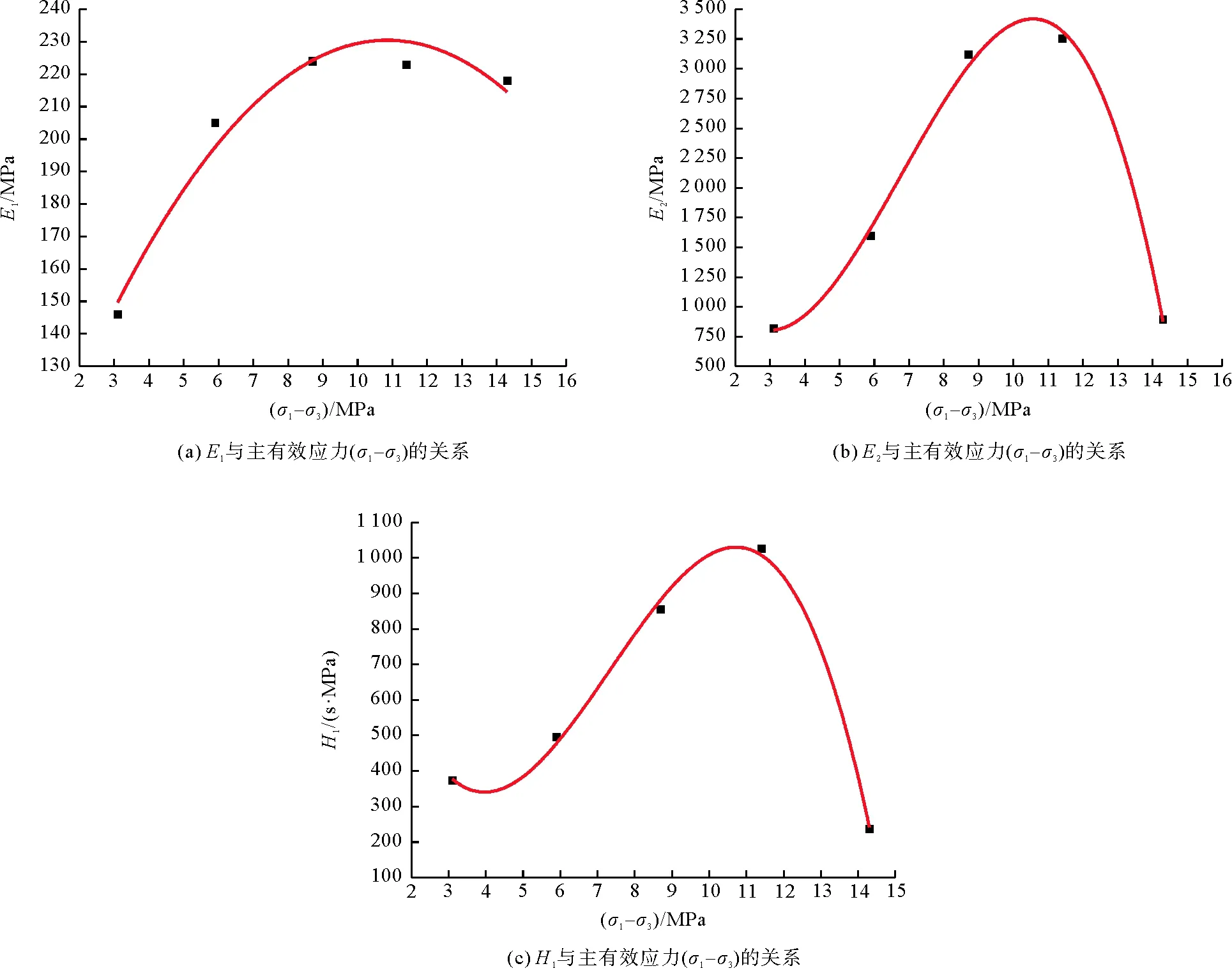
图7 各主要参量值与主有效应力(σ1-σ3)的关系Fig. 7 Relationship between main parameters and main effective stress (σ1-σ3)
3 结论
1) 随着瓦斯压力的梯级增大,含瓦斯煤岩的蠕变变形也相应增大,且呈较为明显的梯级变形,随着围压的梯级增大,含瓦斯煤岩的蠕变变形呈较明显的梯级减小。
2) 在西原体模型的基础上,依据有效应力原理和弹塑性力学中的流动法则构建出含瓦斯煤岩三维蠕变本构方程,所构建方程中不仅将屈服应力σs看作煤岩发生稳定蠕变和不稳定蠕变的特征应力,而且将变形开始加速的时间tα也考虑在内,tα是否存在能够判断含瓦斯煤岩是否会发生不稳定蠕变变形。
3) 利用MATLAB绘制出建立的蠕变本构方程所对应的拟合曲线,将其与试验结果进行对比,拟合程度较好,可以用来表征含瓦斯煤岩的流变过程。通过建立的含瓦斯煤岩三维蠕变本构方程推断出含瓦斯煤岩存在极限变形量,结合试验过程可知,当含瓦斯煤岩的变形量达到该值时,应变速率会在短时间内急剧增大,导致煤岩发生破坏。

