Estimation of the Parameter and Reliability for the Topp-Leone Distribution Under Type-I Doubly Censoring

LONG Qinyi(龙沁怡),XU Liping(徐丽平)

(School of Information and Mathematics,Yangtze University,Jingzhou 434023,China)

Abstract:Firstly,the maximum likelihood estimation,asymptotic confidence interval and Bootstrap confidence interval of the unknown parameter for the Topp-Leone distribution are obtained under Type-I doubly censored samples.Furthermore,the asymptotic confidence interval of the reliability function is also given.Secondly,under different loss functions,Bayesian estimates of the unknown parameter and reliability function are obtained.Monte Carlo simulation is carried out to calculate the mean values and average relative errors of the parameter estimation.Finally,a real life data set is also taken up for illustrative purpose.

Key words:Topp-Leone distribution;Type-I doubly censoring;Maximum likelihood estimation;Bayesian estimation

1.Introduction

Topp and Leone proposed Topp-Leone distribution to fit failure data in [1].Nadarajah and Kotz[2]gave its failure rate function.Topp-Leone distribution has Bathtub shaped failure rate.the mortality rate of human population in infancy is very high due to infant diseases,then it is a constant at some age in adulthood,then it increases again in old age,the graph of the mortality rate is bathtub shaped.Abd-Elmougod et al.[3]estimated the coefficient of variation for Topp-Leone distribution under progressive Type-II censored samples.Some results on statistical inference of stress strength model under Topp-Leone distribution are reported by using frequency method and Bayesian method in [4].In the context of Bayesian set-up,the estimates of parameter and reliability using various prior distributions and different loss functions are discussed in [5-9].

In the statistical inference of reliability and survival analysis,experimental data are often obtained by censoring.Although there have been some research results on statistical analysis of Topp-Leone distribution using complete samples,Type-I or Type-II censored samples in[10-15].However,the estimates of the unknown parameter and reliability for the Topp-Leone distribution under Type-I doubly censored samples have not been reported so far.In this paper,we assume that the lifetimes of the products follow the Topp-Leone distribution.By using different loss functions,the estimates of the parameter and reliability are obtained based on Type-I doubly censored samples.The estimated values of the unknown parameter and reliability are also calculated by stochastic simulation.

2.Maximum Likelihood Estimation

Let the sample observations be independent and identically distributed in the Topp-Leone distribution,and the cumulative distribution function and probability density function are given,respectively,by

whereθis the shape parameter.

Suppose thatXdenotes the lifetime of the product,and follows the Topp-Leone distribution,then its reliability function is obtained asR(x,θ)=1-(2x -x2)θ,0＜x ＜1.In order to understand the reliability indexes of the products,nsamples with failure time following the Topp-Leone distribution are randomly selected for life test.Denote their lifetimes byX1,X2,···,Xn,respectively.Suppose that the test is started from time point zero,the tracking observation is carried out from timet1,and the test is stopped at timet2,satisfy 0＜t1＜t2＜1,at the timet2,all samples without failure are withdrawn from the test.Let

Denote

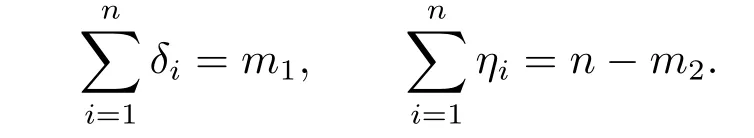
That is to say,in the time intervals (0,t1] and (t2,1),only the number of failed products can be observed,which arem1andn-m2respectively,but the specific failure times are not known,wherem1andm2are random variables.Therefore,the failure times ofnsamples satisfy

3.Interval Estimates of θ and Reliability Function

Sometimes it is necessary to consider the value of unknown parameter in a certain range,which is the confidence interval of parameter.The asymptotic confidence interval and Bootstrap confidence interval of the unknown parameter for the Topp-Leone distribution will be obtained respectively.

Ⅰ Asymptotic confidence interval ofθ

Fisher information reflects the information provided by the population distribution itself,which plays an important role in the study of parameter estimation.Since there is no analytical expression for the MLE ofθ,it is impossible to obtain its exact distribution.However,the asymptotic confidence interval ofθcan be obtained from the asymptotic normality of MLE.From (2.3),the observed Fisher information is obtained by

Ⅱ Bootstrap confidence interval ofθ

There are two methods to construct confidence interval of the parameter by Bootstrap method.One is called percentile Bootstrap (Boot-p) method,which was proposed by Efron(1982);The other is called Bootstrap-t (Boot-t) method,which was proposed by Hall (1982).

(i) The steps of Boot-p method are as follows:

Step 1 Using the method in Section 2,is calculated under Type-I doubly censored samples;

where [x] represents the largest integer not greater thanx.

(ii) The steps of Boot-t method are as follows:

4.Bayesian Estimation

Ⅰ Bayesian estimation ofθ

In Bayesian statistical inference,prior distribution and loss function are two important aspects for the accuracy of parameter estimation,the most commonly used is the squared error loss function.Let’s look at the following lemma.

Lemma 4.1[9]Ifx*=(x1,x2,···,xn) are sample observations from a population distribution,andθis its unknown parameter,then

The prior distribution ofθis taken as the Gamma distribution,and its probability density function is defined by

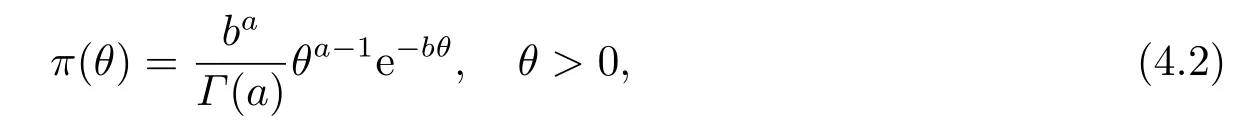
where the hyperparametersa ＞0,b ＞0,andΓ(·) denotes the Gamma function.

Some special prior distributions can be derived from(4.2).Whena=1,π(θ)=be-bθ,θ ＞0 is the exponential distribution.Whena=0 andb=0,π(θ)∝1/θ,θ ＞0 is the generalized prior distribution.Its monotonicity and concavity are related to the value ofa.When 0＜a ≤1,π(θ) is a strictly decreasing function.When 1＜a ≤2,π(θ) is a unimodal function,first convex and then concave.Whena ＞2,π(θ) is a unimodal function,first concave,the middle convex,and finally concave.Therefore,the values ofaandbcan be determined flexibly according to the prior information,which has wide applicability.

From (4.1) and (4.2),the posterior probability density function is obtained as

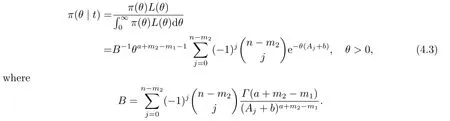
Theorem 4.1Lett=be Type-I doubly censored samples from the Topp-Leone distribution (2.1),if the prior distribution ofθis given by (4.2),the following conclusions can be obtained.

(i) Under the squared error loss function,the Bayesian estimation ofθis obtained by

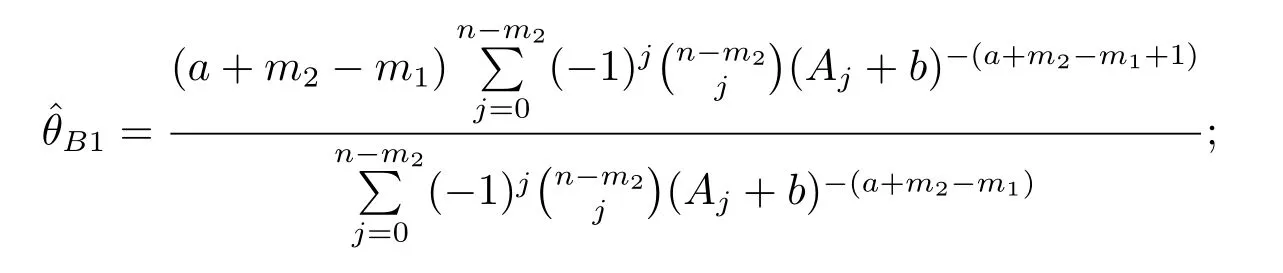
(ii) Under the weighted square loss function,the Bayesian estimation ofθis obtained by

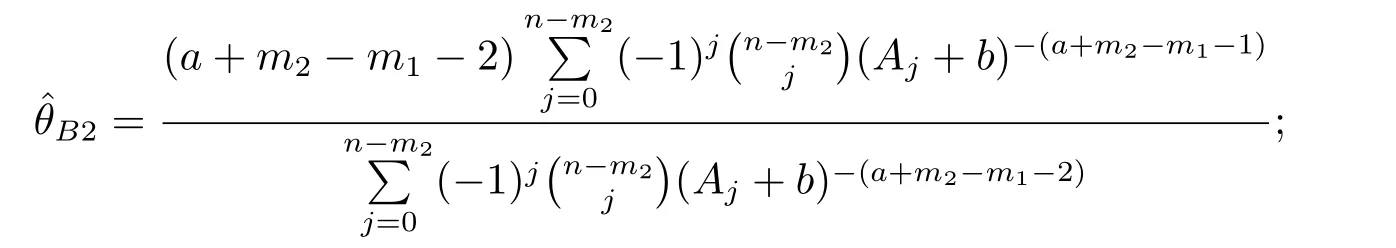
(iii)Under the generalized entropy loss function,the Bayesian estimation ofθis obtained by

Proof(i)Under the squared loss function,the Bayesian estimation ofθis the mean value of its posterior distribution.So we have

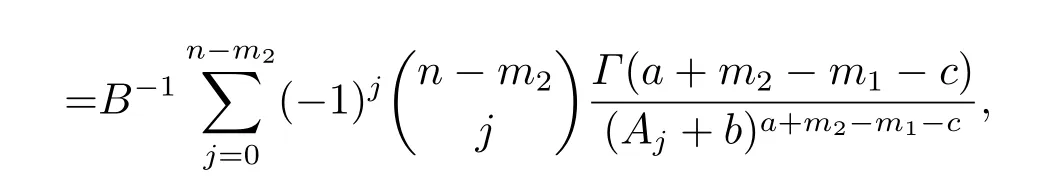
the Bayesian estimation ofθunder the generalized entropy loss function is obtained as

Ⅱ Bayesian estimation of reliability function

From Lemma 4.1,we can obtain the following theorem.

Theorem 4.2Lett=be Type-I doubly censored samples from the Topp-Leone distribution (2.1),if the prior distribution ofθis given by (4.2),we can obtain the following conclusions:

(i) Under the squared error loss function,the Bayesian estimation of the reliability functionR(x) is given by

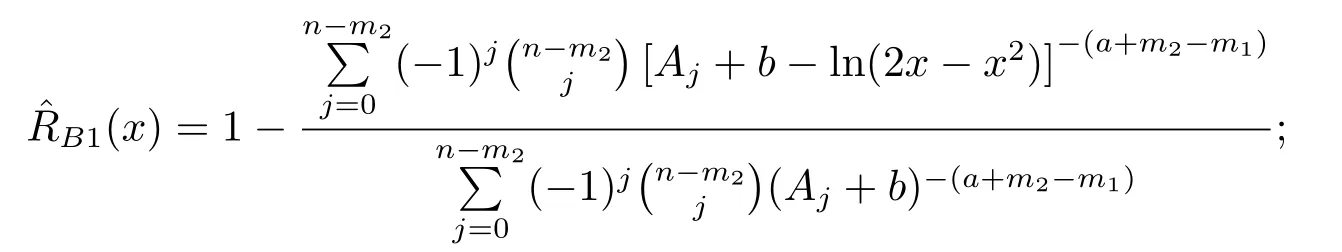
(ii) Under the weighted square loss function,the Bayesian estimation of the reliability functionR(x) is given by

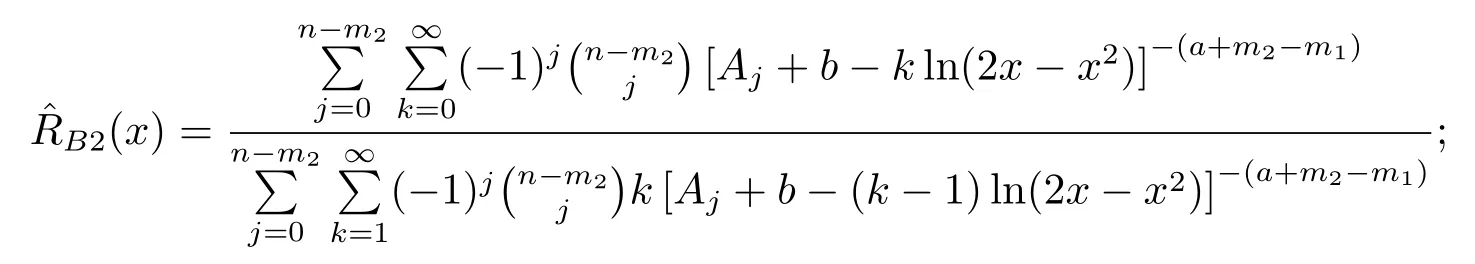
(iii)Under the generalized entropy loss function,the Bayesian estimation of the reliability functionR(x) is given by

Proof(i) Under the squared loss function,the Bayesian estimation ofR(x) is

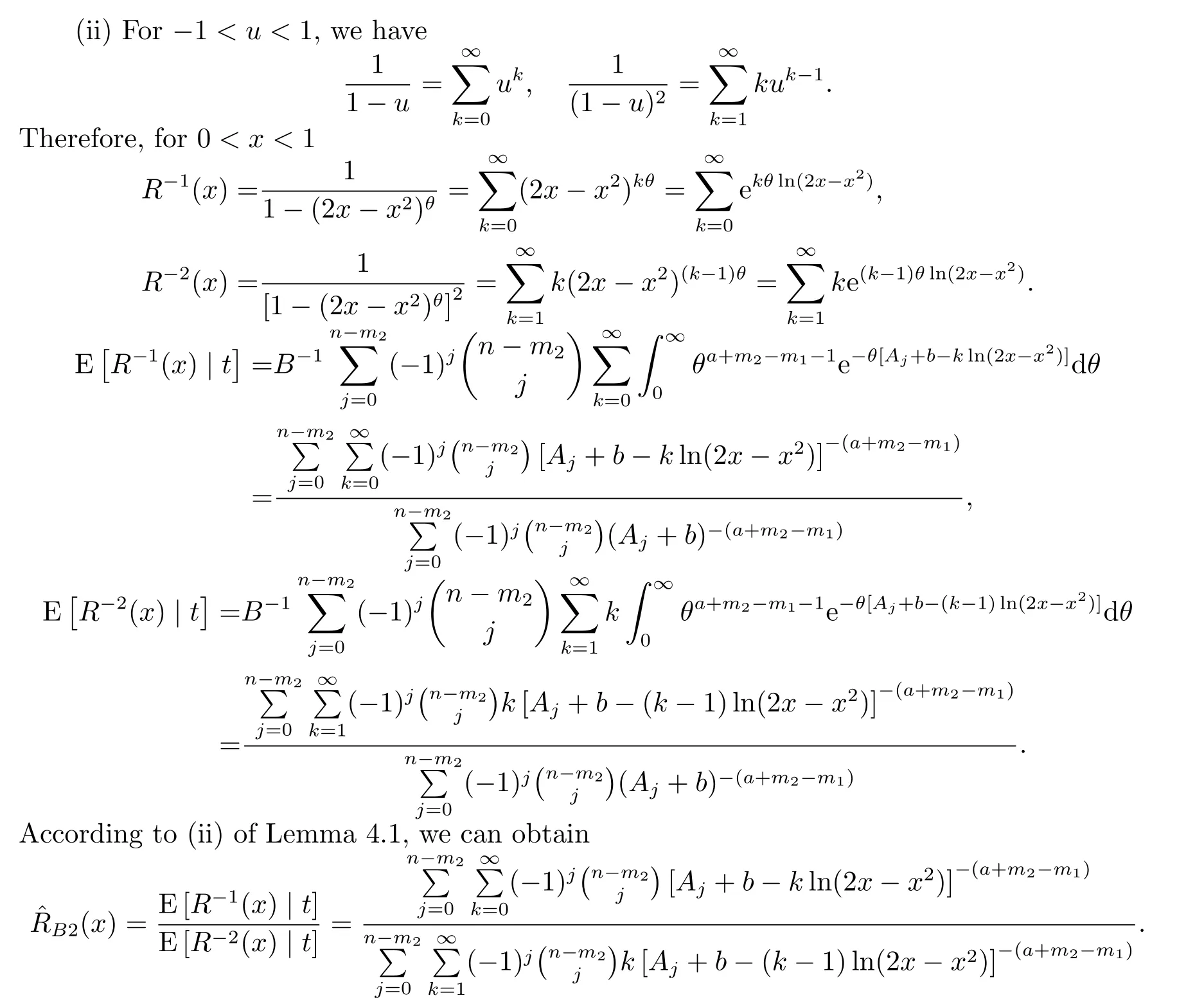
(iii)According to Lemma 4.1,it is not difficult to obtain the conclusion(iii)by using the definition of mathematical expectation.

5.Simulation Study

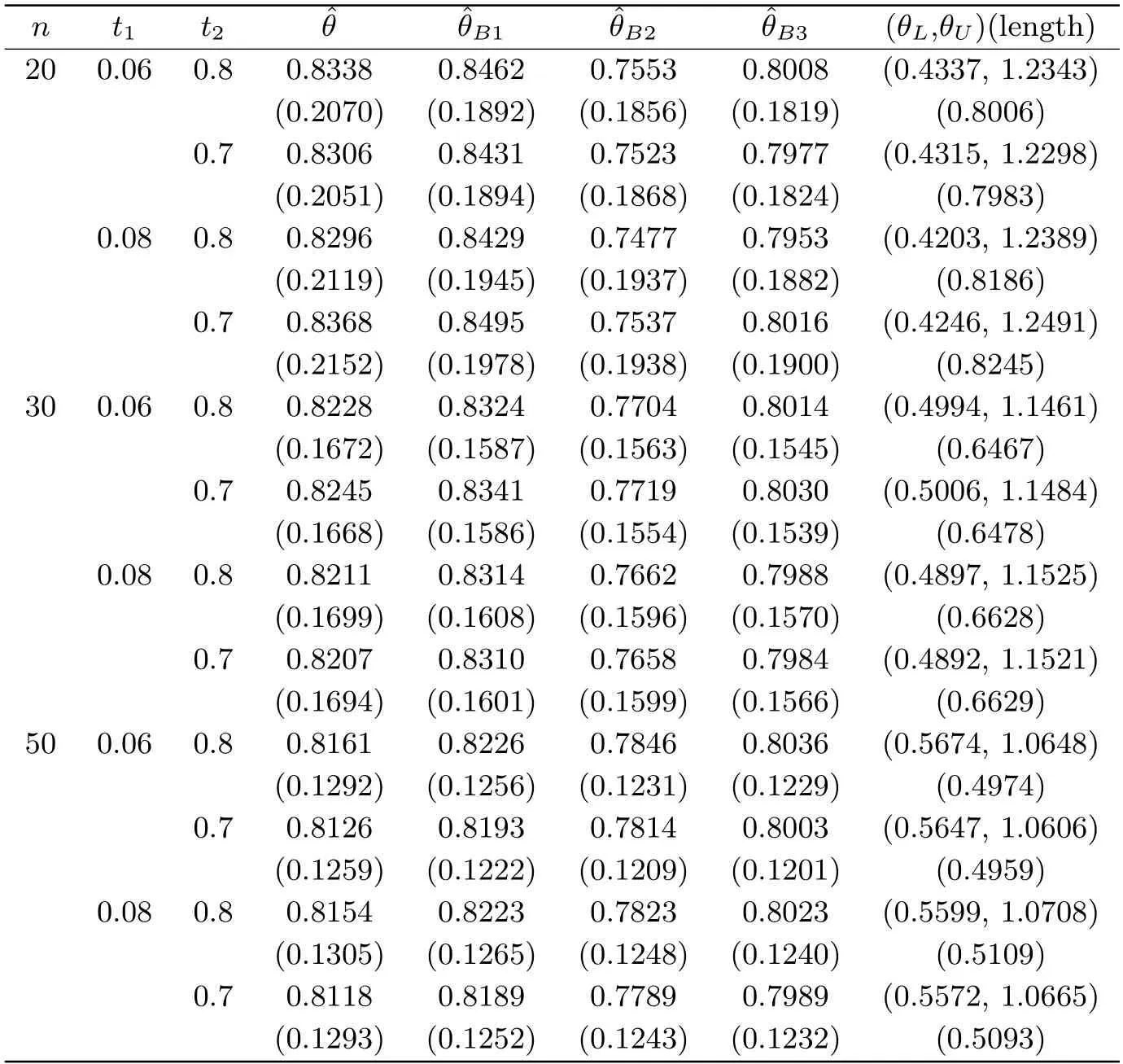
Letr1,r2,···,rnbe independent random numbers from the uniform distributionU(0,1).Whenθ=0.8,according to the cumulative distribution function (2.1),and use the inverse function method,thenxi=1-(i=1,2,···,n) are random numbers from the Topp-Leone distribution.Given the values oft1andt2,Type-I doubly censored samples can be obtained.The values of the two hyperparameters are taken asa=2 andb=2,statistical inference is carried out by using the obtained samples.If the above process is repeated 10000 times,the mean values and average relative errors (in parenthesis) of various point estimates forθcan be obtained.In addition,the average lower limits and average upper limits of the 95%confidence intervals forθcan also be obtained.The simulation results are shown in Table 5.1.

Ift1andt2are kept unchanged,it can be seen from Table 5.1 that with the increase of sample sizen,the average relative errors of various estimates forθgradually decrease.The average length of confidence intervals forθalso gradually decrease.This reflects the consistency of various estimates forθ.

Tab.5.1 Mean values and average relative errors of parameter estimation,the average confidence limits

6.Data Analysis

The following real life data is taken from Mazumdar and Gaver[16]concerning unit capacity factor.The data set consisting of 23 such observations is reported below:0.853,0.759,0.866,0.809,0.717,0.544,0.492,0.403,0.344,0.213,0.116,0.116,0.092,0.070,0.059,0.048,0.036,0.029,0.021,0.014,0.011,0.008,0.006.According to [17],the above data set has passed the Kolmogorov-Smirnov hypothesis test.It can be considered that these data come from the Topp-Leone distribution (2.1),and the MLE ofθis 0.5943.The correlation estimates ofθandR(x) are calculated under different Type-I doubly censored samples,which are listed in Tables 6.1-6.2.

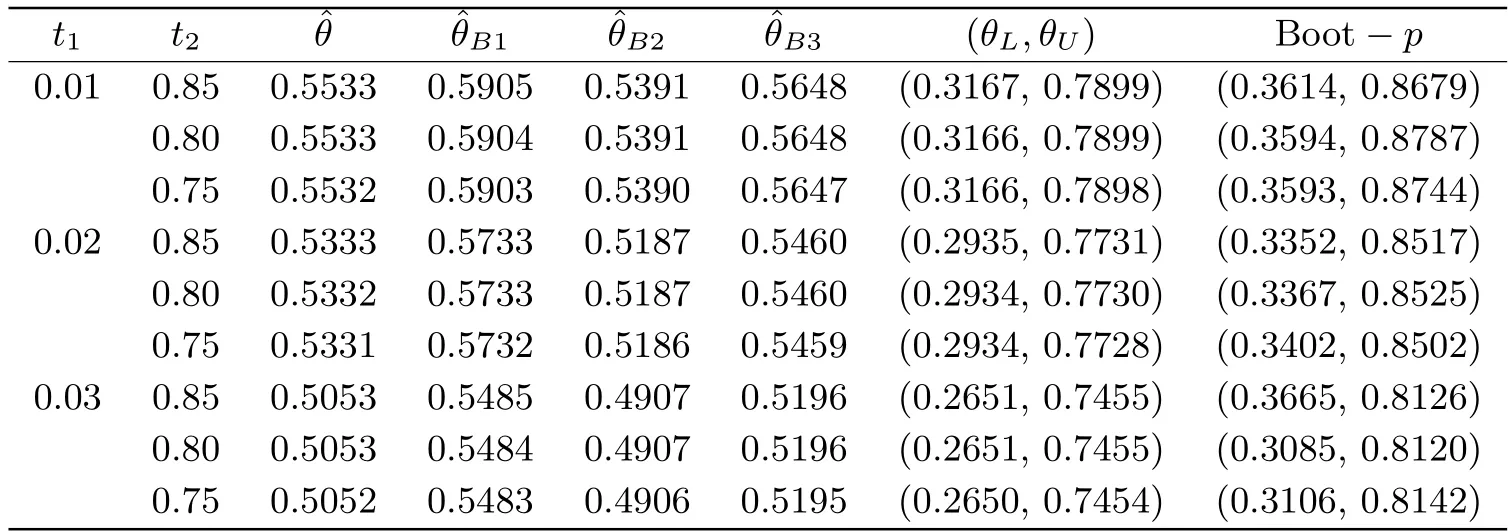
Tab.6.1 Estimates of θ (a=2,b=1,c=1)

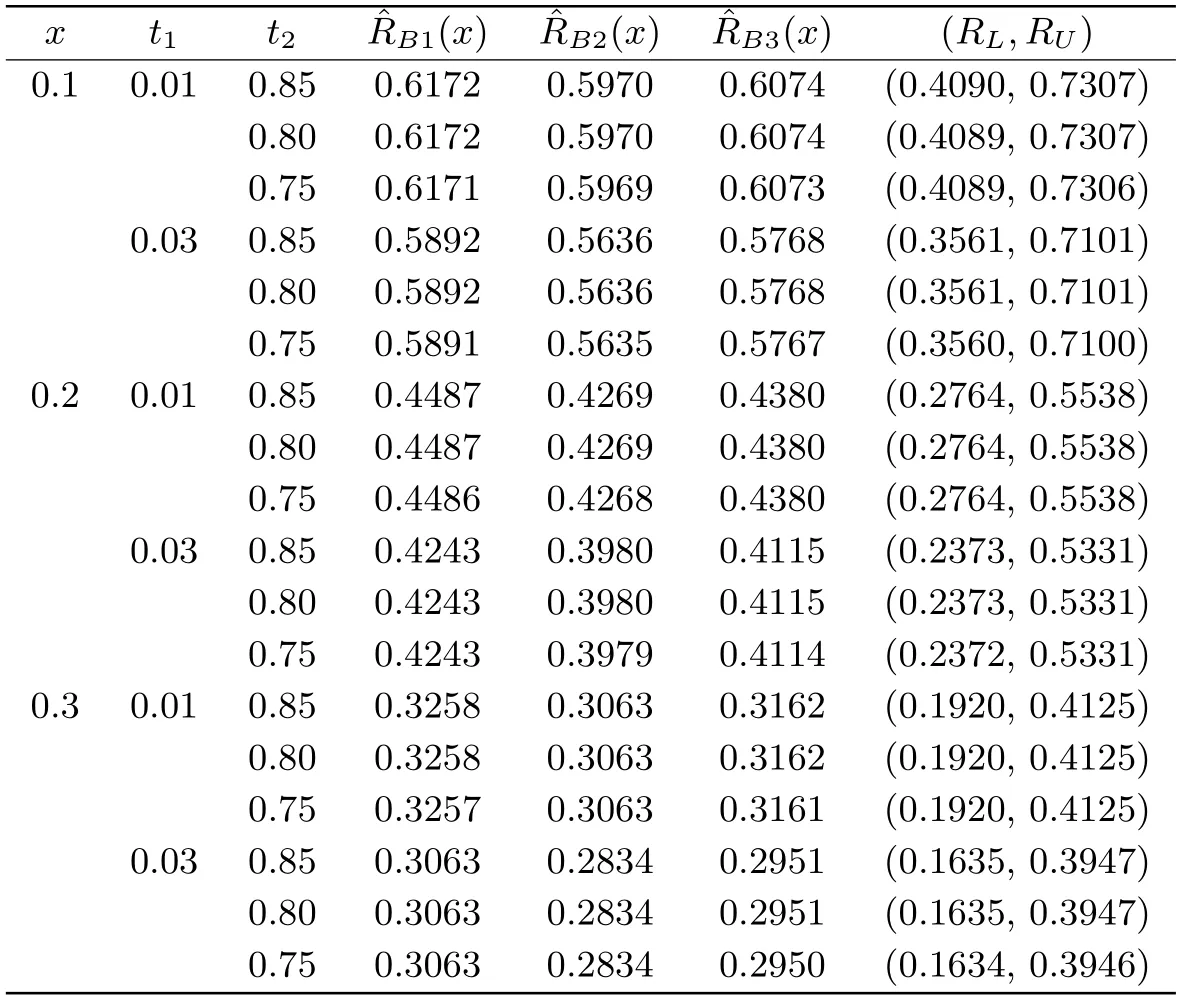
Tab.6.2 Estimates of R(x)(a=2,b=1,c=1)

It can be seen from Tables 6.1-6.2 that whent1is fixed,with the decrease oft2,the various estimates ofθandR(x) all change little,and the change oft1has a great influence on the estimates ofθandR(x).

7.Conclusions

The Topp-Leone distribution is a kind of life distribution,which can be used to fit failure data.In recent years,some research results on this distribution have been produced.In this paper,we discuss the estimates of the parameter and reliability for the Topp-Leone distribution under Type-I doubly censored samples.The estimates of the parameter and reliability are calculated by using classical statistical theories and Bayesian theories respectively.The mean values and average relative errors of various estimates are obtained by stochastic simulation,the results show that the accuracy of various estimates is improved with the increase of sample size.In addition,we can also consider hierarchical Bayesian estimation or E-Bayesian estimation forθandR(x).