CMIP6与CMIP5全球气候模式对中国东北地区气温模拟性能的比较评估

何夏曼, 姜超*, 汪君, 王襄平

1 北京林业大学生态与自然保护学院, 北京 100083 2 中国科学院大气物理研究所竺可桢-南森国际研究中心, 北京 100029

0 引言

观测事实表明,自工业革命以来,全球范围内气温在显著上升(苏京志等,2016),其对自然生态系统及社会经济发展产生的影响引起国内外广泛关注 (Chen, 2013). 中国东北地区处于北半球的中高纬度,对气候变暖响应敏感(本文所述东北地区为狭义的东北地区,即东北三省).该地区的气温在1956—2017年间显著上升,平均气温倾向率为0.327 ℃/10 a(吴金华等, 2021),是全国最显著增温的地区之一(任国玉等, 2005; 贺伟等, 2013; 吴金华等, 2021).同时,作为我国最重要的商品粮食基地之一,东北地区气温的显著增高已成为东北粮食生产过程中的一个重要威胁 (周梦子等, 2017),十分有必要开展对此地区未来气温变化的科学研究,为今后的粮食生产提供科学指导.

世界气候研究计划(World Climate Research Programme,WCRP)的耦合模式比较计划(Couple Model Inter-comparison Project,CMIP)已成为气候预估的最重要手段之一(Papalexiou et al., 2020; Chen et al., 2020).它以“推动模式发展和增进对地球气候系统的科学理解”为目标,有助于我们加深对气候变化的认识和理解(周天军等, 2019).但由于气候系统的复杂性以及模式自身存在的系统误差,使全球模式模拟的结果与实际观测值有所偏差.因此,在对未来气候做预估之前,需从多变量、多指标、多过程对模式的模拟结果进行综合定量评估(赵宗慈等, 2013; 周文翀和韩振宇, 2018).气温作为最基本的气候要素之一(Sun and Ao, 2013),在气候模式的评估中一直受到大家的关注(云翔等, 2020).近年来,基于CMIP5模式模拟气温的结果,已有学者在中国东北地区开展了一系列模式评估工作.陶纯苇等(2016)利用CMIP5中45个气候模式资料进行系统的评估,指出CMIP5模式能够较好地模拟出中国东北地区由南至北气温逐渐降低的空间分布特征,多模式集合结果与观测的差值基本在-1～0.5 ℃之间.崔妍等(2013)也得出相似的结论,并指出多模式集合模拟年平均气温气候态空间分布的等温线更为平直,这可能与CMIP5模式空间分辨率低有关.敖雪等(2021)通过比较RegCM4区域气候模式与CMIP5模式对中国东北气温的模拟结果发现,CMIP5模式对气温年际变化的模拟能力有限,这与CMIP5模式在全国(Guo et al., 2013)和全球(魏萌和乔方利, 2016)尺度上的模拟能力相似.

如今,耦合模式比较计划已经进入第六阶段(CMIP6).与CMIP5相比,CMIP6参与的模式数量更多,设计的数值实验更丰富,所提供的模拟数据更为庞大(Eyring et al., 2016; O′Neill et al., 2016; 张丽霞等, 2019; 周天军等, 2019).Chen等(2020)通过比较CMIP6中的12个模式及其在CMIP5中对应的早期版本发现,CMIP6中大部分模式对中国极端气候的模拟能力有所提高.Jiang等(2020)在0.5°×0.5°水平分辨率上分别评估了49个CMIP5模式与43个CMIP6模式对于1961—2005年中国气温与降水的模拟能力,认为CMIP6模式对我国气温、降水的气候态空间分布具有较好的模拟能力,其模拟结果优于CMIP5模式.You等(2021)将中国分成四个子区,发现CMIP6模式对中国地表年平均温度存在低估现象,但均能较好地反映其空间分布,尤其是对中国北方的模拟能力较高.可见,CMIP6模式对不同区域模拟能力存在差异,需要针对不同区域开展深入研究.

不同模式间模拟结果的差别反映了模式间的差异与不确定性,它主要来自模式自身对物理过程描述的差异(张艳武等, 2016).而多模式集合平均方案可以将模式之间的偏差相互抵消,使得模拟结果比单模式的模拟结果更优(周文翀和韩振宇, 2018; Pierce et al., 2009).已有学者发现通过择优筛选后的多模式集合平均方案比所有模式集合平均方案的模拟结果要更优(蒋帅等, 2017; 王涛等, 2020),且一般也优于绝大多数单模式的模拟结果(崔妍等, 2013; 陶纯苇等, 2016).因此,有越来越多的研究开始分析多模式集合模拟结果的可靠性(Pierce et al., 2009; Chen and Sun, 2009; Yang et al., 2021).Pierce等(2009)发现不同数量模式的集合方案模拟能力有所差异,并指出14个模式作为样本进行多模式集合平均的方案能够抵消不同模式的模拟误差,使模拟效果较优.

目前,关于CMIP6模式对中国东北地区气温模拟能力的评估工作仍然较少.CMIP6模式对中国东北地区气温的模拟相比于CMIP5是否有所改进？围绕这个问题,本文利用CN05.1观测资料、34个CMIP6模式与39个CMIP5模式数据,评估两代模式与优选模式集合方案对中国东北地区(1961—2005年)气温的模拟能力,为预估中国东北地区未来气候变化提供可靠的科学依据.

1 数据与方法

1.1 全球气候模式资料与观测资料

本文使用CN05.1气温数据作为观测数据,选取时间跨度为1961—2005年.该数据是根据2400余个中国地面气象台站的观测资料所建立起来的网格数据,水平分辨率为0.25°×0.25°(吴佳和高学杰, 2013).

本文分别选取CMIP5中39个模式和CMIP6中34个模式的历史模拟数据,进行年平均气温的比较评估,时间跨度为1961—2005年,并选取中国东北地区(黑龙江省、吉林省、辽宁省)作为研究区.表1为本研究中所使用的全球气候模式资料的相关简介,模式编号5-1-39为CMIP5模式,模式编号6-1-34为CMIP6模式; 其中,模式5-1至5-16为模式6-1至6-16对应的早期版本(数据来源: https:∥esgf-node.llnl.gov/search/cmip6/; https:∥esgf-node.llnl.gov/search/cmip5/).

由于各模式的输出数据与观测数据的水平分辨率不相同,为了方便比较各模式间及模式与观测资料之间的差异,将模式的输出数据统一双线性插值(胡芩等, 2014)到与观测数据相同的水平分辨率(0.25°×0.25°)上.

1.2 地形校正

由于不同模式所使用的地形资料与水平分辨率不同,在进行双线插值的过程中会因地形起伏而带来偏差.为了消除地形所带来的偏差,本研究对双线性插值后的模式气温进行地形校正(Zhao et al., 2008; 张蓓和戴新刚, 2017).地形校正方程为

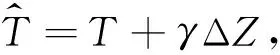
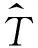
1.3 评估方法

(1) 泰勒图

泰勒图(Taylor, 2001)是模式评估中广泛应用的方法,主要基于相关系数、均方根误差和标准差之比三个指标,比较模式模拟结果与观测之间的相似程度与差异的大小.当相关系数越大,均方根误差越小,模式与观测的标准差之比越接近于1时,即在图上模拟点越接近观测点,模式的模拟能力越强.本文对观测数据与模式数据先进行标准化处理,再采用泰勒图,从区域平均气温的多年变化、年平均气温气候态的空间分布、年平均气温气候倾向率的空间分布这三个方面,对CMIP5与CMIP6模式的模拟能力进行评估.

(2) 技能得分

在泰勒图中,如果模式模拟结果与观测的相关系数和标准差之比均降低,就难以判断模式的模拟性能是否改进.因此,本文引入泰勒提出的技能得分(Taylor, 2001)(S值),用以定量评估模式对气温的模拟能力,并从区域平均气温的多年变化、年平均气温气候态的空间分布和年平均气温气候倾向率的空间分布这三个方面分别对模式的模拟能力进行排名.S值的计算公式为

式中,R为模式模拟结果与观测间的相关系数,R0为模式模拟结果与观测间相关系数的最大值,σm与σo分别为模式模拟结果与观测资料的标准差.S值的取值范围为0～1,S值越接近1,模式模拟能力越强.

(3) 综合评级指标

除S值以外,本文还使用综合评级指标(Mr)(Schuenemann and Cassano, 2009)对CMIP5与CMIP6模式的综合模拟能力进行排名.模式的综合模拟能力越强,Mr越接近于1.Mr的计算公式如下：

表1 模式的基本信息Table 1 Brief introduction of the models

式中,a为CMIP5或CMIP6参与评估的模式个数;b为评估指标的个数,本文使用了模式在区域平均气温的年际变化、年平均气温气候态的空间分布、年平均气温气候倾向率的空间分布的3个S值作为评估指标,因此b=3;ri为各模式对区域平均气温的多年变化、年平均气温气候态的空间分布、年平均气温气候倾向率的空间分布模拟的S值排名,例如,根据S值,ACCESS-ESM1-5(模式编号6-1)模拟区域平均气温的年际变化的排名为3,其r1为3.

1.4 最优模式集合方案的设计

本文通过Mr对CMIP5与CMIP6中的单模式综合模拟能力进行排名.在CMIP6的34个模式中,分别对前2名、前3名…前34名模式进行等权重集合平均(赵宗慈等, 2013; 陶纯苇等, 2016; Chen et al., 2020),得到34种优选模式集合平均.根据Mr的大小,选择34个优选模式集合平均中综合模拟能力最高的方案所对应的模式个数,作为后续评估最优模式集合平均模拟能力的模式个数.CMIP5的39个模式也采用相同的方法,确定最优模式集合平均的模式个数.

2 1951—2005年中国东北地区气温模拟结果评估

2.1 单模式模拟结果评估

(1) 区域平均气温多年变化特征

图1为1961—2005年CMIP5模式与CMIP6模式对中国东北地区区域平均气温多年变化的模拟结果,其中黑色实线为观测值,每年的箱线图表征了模式模拟结果的范围.观测数据表明,中国东北地区年平均气温在0～3 ℃之间波动.CMIP5的39个模式模拟区域平均气温中值的多年变化范围在-0.84～0.71 ℃,其模拟结果存在低估现象; CMIP6的34个模式模拟区域平均气温中值的多年变化范围为-0.6～1.3 ℃,其模拟结果比CMIP5更接近观测值.同时,CMIP5的39个模式模拟区域平均气温的范围在-6～6 ℃之间,比CMIP6的34个模式模拟的范围(-5～4 ℃)要更大,说明CMIP6模式模拟年平均气温多年变化的一致性更高,这在CMIP6模拟东南亚地区气温与降水(Hamed et al., 2022)、澳大利亚极端温度(Deng et al., 2021)的结果中也有所体现.他们认为,与CMIP5模拟结果相比,CMIP6模式的不确定性要低得多,模拟结果更一致.

表2为1961—2005年CMIP5和CMIP6模式模拟的中国东北地区区域平均气温线性趋势.观测资料显示,东北地区呈显著增温趋势,其线性趋势为0.43 ℃/10a(p<0.001).CMIP5的39个模式均能模拟出增暖趋势,模拟的线性趋势结果在0.02～0.65 ℃/10a之间,其中,有30个模式模拟的增暖趋势通过显著性检验(p<0.05).所有CMIP5模式模拟的线性趋势平均值为0.23 ℃/10a,中位数为0.22 ℃/10a,比观测数据要低.CMIP5中模拟增温趋势大小与观测最接近的模式为CanESM2(模式编号5-3),模拟值为0.42 ℃/10a.而CMIP6的34个模式模拟的线性趋势结果分布在-0.05～0.49 ℃/10a之间,其中有25个模式模拟的增温趋势通过显著性检验(p<0.05).CMIP6所有模式模拟的线性趋势平均值为0.26 ℃/10a,中位数为0.31 ℃/10a,比CMIP5模式模拟结果的更接近观测.其中,CMIP6中对增温趋势模拟最好的模式是CanESM5(模式编号6-3)和NorESM2-MM(模式编号6-32),其模拟的线性趋势分别为0.44 ℃/10a和0.42 ℃/10a.虽然CMIP5与CMIP6的模式大部分都能模拟出增温趋势,但普遍存在低估现象,CMIP5的低估程度更大.CanESM2(模式编号5-3)及CanESM5(模式编号6-3)在这两阶段中模拟结果均较好.

图1 1961—2005年CMIP5(a) 与CMIP6 (b) 模式模拟中国东北地区区域平均气温多年变化箱线图 图中黑色实线为观测数据,箱线图由上至下为最大值、第75百分位数、中位数、第25百分位数和最小值.Fig.1 Time series of regionally averaged surface temperature over the three provinces in Northeast China for the CMIP5(a) and CMIP6 (b) models during 1961—2005 Black solid lines indicate the observation. The box indicates the 25th and 75th percentiles, a bar indicates the 50th percentile, and whiskers indicate the max and min datum.

表2 1961—2005年CMIP5、CMIP6模式模拟的中国东北地区年平均气温线性趋势Table 2 Linear trends of annual mean surface air temperature over the three provinces in Northeast China for the CMIP5 and CMIP6 models during 1961—2005

为了进一步评估和比较CMIP5与CMIP6模式对中国东北地区区域平均气温多年变化模拟能力的差异,本文使用泰勒图来评估模式模拟性能(图2).就模式与观测的相关系数而言,39个CMIP5模式模拟结果与观测的相关系数介于0.1～0.5之间,其中21个模式与观测的相关系数大于0.3; 而CMIP6所有模式的模拟结果与观测的相关系数集中在0.3～0.5之间,比CMIP5单模式的模拟结果要更优.从模拟结果与观测的标准差之比来看,CMIP5模式模拟结果与观测的标准差之比在0.3左右,而CMIP6模式的模拟结果与观测的标准差之比在0.4左右,其比CMIP5模式的模拟效果更优.从模拟结果与观测的均方根误差来说,CMIP5与CMIP6模式的模拟结果与观测的均方根误差都相对集中在1.0～1.2之间.总的来说,CMIP6模式对区域平均气温的模拟能力优于CMIP5模式.

(2) 年平均气温气候态与气候倾向率的空间分布

图3为1961—2005年中国东北地区CMIP5与CMIP6模式模拟的年平均气温气候态空间分布和年平均气温气候倾向率空间分布相对于观测的泰勒图.对于年平均气温气候态空间分布而言(图3a—b),CMIP6的34个模式的模拟结果一致性较高,体现为相对应的点在泰勒图中分布更为集中.29个模式与观测的相关系数大于0.95,31个模式与观测的均方根误差小于0.5; CMIP5的39个模式也很好地模拟出了中国东北地区的年平均气温气候态,表现在27个模式的模拟结果与观测的相关系数大于0.9,25个模式的模拟结果与观测的均方根误差小于0.5,但与CMIP6模式相比,CMIP5模式模拟结果之间的差异较大,且模拟能力没有CMIP6模式优.从年平均气温气候倾向率的空间分布的模拟能力来看(图3c—d),CMIP5的39个模式中,有17个模式的模拟结果与观测的相关系数大于0.5,仅有8个模式模拟结果与观测的均方根误差小于0.75; 对于CMIP6的34个模式而言,20个模式的模拟结果与观测的相关系数大于0.5,15个模式的模拟结果与观测数据的均方根误差小于0.75.CMIP5与CMIP6模式对年平均气温气候倾向率的空间分布模拟能力都较低,但相比于CMIP5模式,CMIP6模式的模拟结果更为理想.

图2 1961—2005年中国东北地区CMIP5 (a)、CMIP6 (b)模式模拟的区域平均气温相对于观测的 区域平均气温多年变化的泰勒图 图中黑色空心点为观测值.Fig.2 Taylor diagrams for time series of regionally averaged surface air temperature of the three provinces in Northeast China between CMIP5 (a), CMIP6 (b) models and observations for the period 1961—2005 Black hollow dots indicate observation.

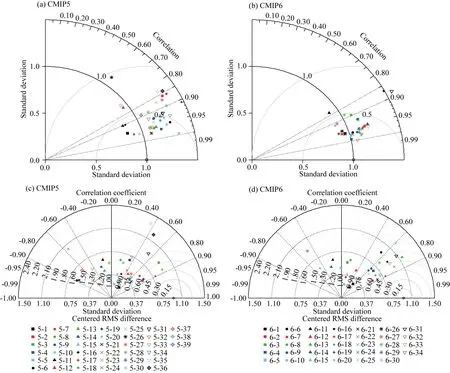
图3 同图2,但为年平均气温气候态(a,b)与年平均气温气候倾向率(c,d)空间分布的泰勒图Fig.3 Same asFig.2,but Taylor diagram for spatial distributions of annual mean surface air temperature (a,b) and its trends (c,d)

2.2 最优模式集合平均对中国东北地区气温的评估

(1) 最优模式集合平均方案的设计

为了筛选模拟性能较好的模式做优选模式集合平均,本文通过S值,将CMIP5与CMIP6模式模拟能力量化,尤其关注CMIP6模式和它在CMIP5中早期版本S值的变化.从表3可以看出,相比于CMIP5,CMIP6模式整体上在区域平均气温多年变化、年平均气温气候态空间分布和年平均气温气候倾向率空间分布的模拟结果均有所进步,平均S值为0.54、0.91及0.49(CMIP5的平均S值分别为0.51、0.84及0.28).CMIP6及相应模式在CMIP5中早期版本的模拟能力相比较,有9个CMIP6模式(占共有模式个数的56.3%)比其在CMIP5中的早期版本对区域平均多年变化模拟结果的S值有所升高,其中,模拟能力进步最大的模式为MPI-ESM1-2-LR(模式编号6-14),S值从0.242提升到0.776.从年平均气温气候倾向率空间分布的模拟结果来看,有8个模式(占共有模式个数的50%)的模拟能力相对于CMIP5中的早期版本有所提高,且其S值提高的平均幅度(0.488)要大于模式对区域平均气温多年变化模拟结果的S值提高的平均幅度(0.267),其中,提高幅度最大的模式为MPI-ESM1-2-LR(模式编号6-14),S值从0.012提升到0.856.对于年平均气温气候态空间分布的模拟结果而言,有14个CMIP6模式(占共有模式个数的87.5%)相对于CMIP5中的早期版本的模拟能力有所提升,提升幅度最大的为FGOALS-g3(模式编号6-7),S值从0.705提升到0.930,有进步的模式的S值提升幅度平均值为0.073.相反,一些模式对气温的模拟能力比其在CMIP5中的早期版本有所下降,如CanESM5(模式编号6-3)对区域平均气温多年变化、年平均气温气候态空间分布及年平均气温气候倾向率空间分布的模拟能力均下降.总体来看,CMIP6的大部分模式比CMIP5的早期版本模拟性能有所提高,这在Chen等(2020)研究CMIP6对中国极端气候模拟性能中也得出相似的结论.

已有研究指出模式个数会影响多模式集合平均的模拟能力(Pierce et al., 2009).因此,本文引入Mr,分析在不同模式个数的情况下,优选集合方案的综合模拟能力的高低,此指标已被广泛运用于模式评估中(蒋帅等, 2017; Schuenemann and Cassano, 2009).Mr的计算是基于S值对区域平均气温的多年变化、年平均气温气候态空间分布、年平均气温气候倾向率空间分布这三个方面的排名,它的高低表示了优选模式集合平均对这三个方面的综合模拟能力,如果这三个方面的S值排名相互之间的相关性过高,就会导致S值排名的评分权重偏大或偏小.本文在使用Mr来评估优选模式集合平均的综合模拟能力之前,先分别对CMIP5与CMIP6中基于S值对区域平均气温的多年变化、年平均气温气候态空间分布、年平均气温气候倾向率空间分布的排名进行了两两相关性检测,结果发现相关系数均不超过0.4,且大部分未通过显著性检验,因此,本文使用Mr作为评估指标是可靠的.

由图4可以看出,无论是CMIP5还是CMIP6,优选集合方案的模拟能力与模式个数的关系都不是简单的正相关关系.随着模式个数的增多,在相同模式个数的条件下,CMIP6模式优选集合方案的模拟能力一般要高于CMIP5,其模式模拟能力下降的速率也要低于CMIP5,且最终会保持在一个较为稳定的水平,而CMIP5的优选集合方案随着模式个数的增多,模拟能力呈现先上升后下降的趋势.从优选集合方案的综合模拟能力来说,随着模式个数的增加,CMIP5与CMIP6优选集合方案的Mr逐渐升高,说明随着模式的增加,优选集合方案的模拟能力也在上升,这与Pierce等(2009)所得出的结论相似.他们通过CMIP3的21个模式对美国西部地区的日最低气温进行了归因分析,发现多模式集合的模拟效果会随着集合样本数量的增加而升高,周文翀和韩振宇(2018)在中国黄河流域使用绝对误差、均方根误差、秩评分等评估指标也得到了类似的结论.CMIP5与CMIP6优选集合的Mr值均在模式个数为12左右达到峰值(图4d),随后逐渐下降.这说明当使用综合模拟能力最佳的12个模式做集合平均时,能够最好地模拟出中国东北地区的气温特点.但在其他地区,使用不同的评估指标对不同气候变量进行研究,该结论是否仍然成立,需要进一步的研究,如对于美国西部的日最低气温而言,Pierce等(2009)使用均方根误差、技能得分等评估指标对CMIP3的模拟能力进行评估,认为未经过优选的CMIP3多模式集合模拟效果将随着随机集合样本增加而提高,且在达到一定样本数量之后逐渐稳定.他认为模式个数至少为14才能够保证不同气候模式的模拟误差相互抵消,提高多模式集合模拟效果的可信度.

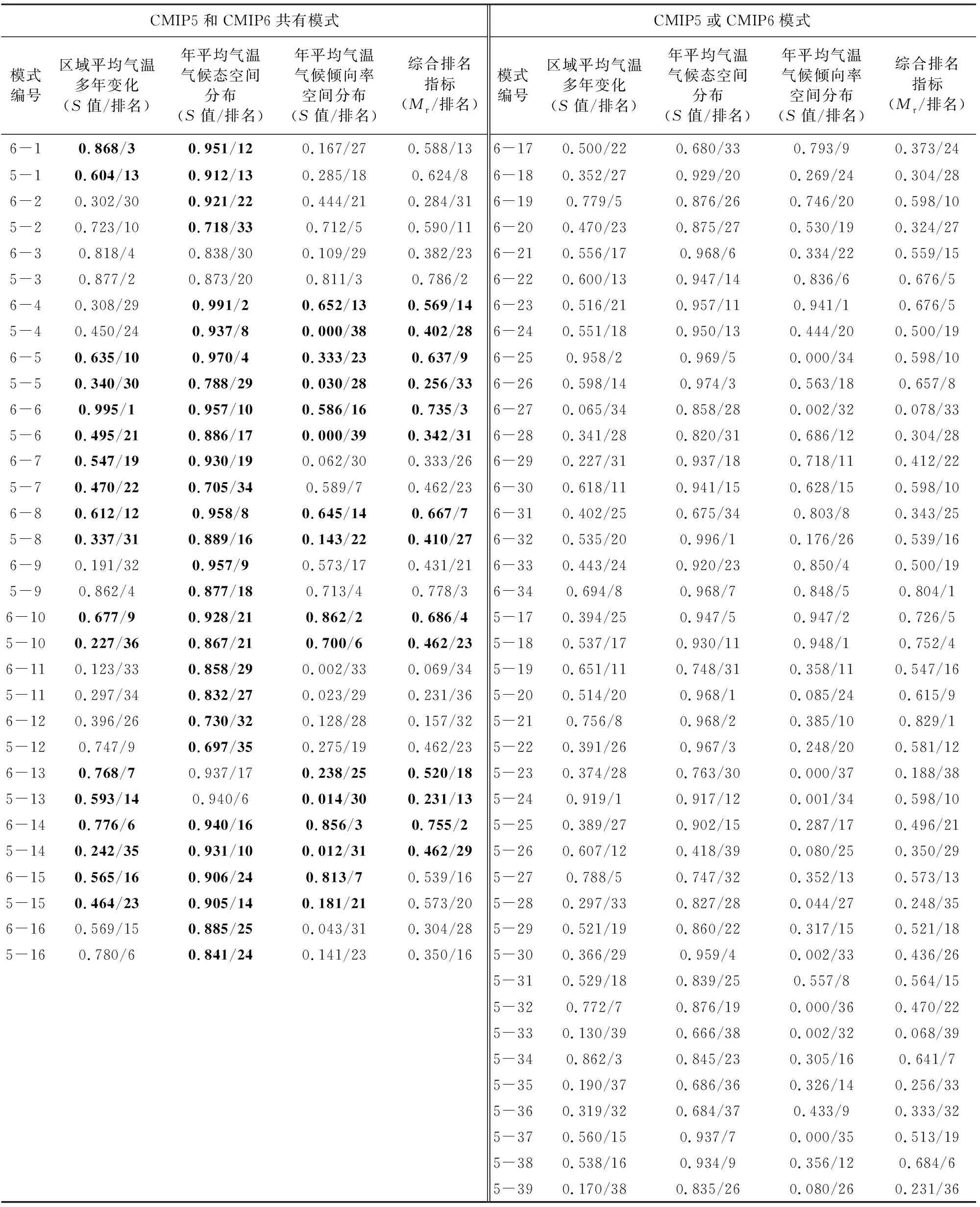
表3 CMIP5模式、CMIP6模式对区域平均多年变化、年平均气温空间分布和年平均气温气候倾向率 空间分布的S值与MrTable 3 The interannual variations of regionally averaged surface air temperature, the spatial distributions of annual mean air surface temperature and the trends for the CMIP5 and CMIP6 models by a comprehensive metric proposed by Taylor and composite rating indicator

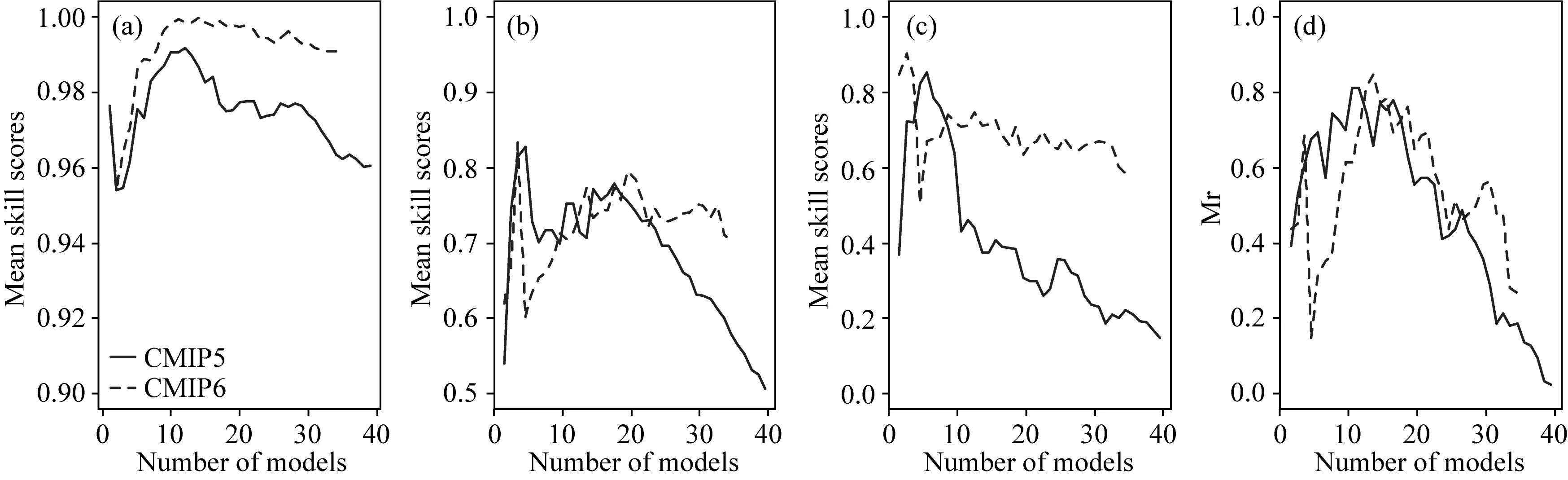
图4 不同模式的个数对优选模式集合平均方案模拟能力的影响. (a—c) 分别为基于S值的优选模式集合平均对年平均气温气 候态空间分布、区域平均气温多年变化及年平均气温气候倾向率的模拟能力. (d) 为基于Mr的优选模式集合平均的模拟能力Fig.4 The influence of the number of ensemble members on the models′ capability for spatial distributions of annual mean surface air temperature (a), interannual variations of regionally averaged surface air temperature (b) and spatial distributions of annual mean surface air temperature trends (c) based on the S value (a—c) and Mr (d)

本文最终通过Mr,筛选出CMIP5与CMIP6中综合模拟能力前12名模式,其中,CMIP5模式的前12名为：CESM1-BGC,CanESM2,GFDL-ESM2M,BCC-CSM1-1-M,ACCESS1-3,MPI-ESM-P,MIROC4h,ACCESS1-0,CCSM4,CMCC-CM,BCC-CSM1-1,CESM1-FASTCHEM; CMIP6选中的模式为：TaiESM1,MPI-ESM1-2-LR,CMCC-CM2-HR4,GISS-E2-1-H,E3SM-1-0,E3SM-1-1,GFDL-CM4,GISS-E2-1-G,CESM2-WACCM,CESM2-FV2,FGOALS-f3-L,NESM3.CMIP5与CMIP6前12名模式分别在等权重系数条件下集合平均,得到CMIP5(MME5)与CMIP6最优模式集合平均方案(MME6).

(2) 最优模式集合平均模拟结果

图5a为CMIP5与CMIP6的最优模式集合平均模拟的区域平均气温多年变化、年平均气温气候态空间分布及年平均气温气候倾向率空间分布相对于观测的泰勒图.MME6对区域平均气温多年变化的模拟能力没有明显进步,然而,相比于MME5,MME6能更好地模拟出年平均气温气候态及气候倾向率的空间分布,在开展对中国东北地区年平均气温气候态及气候倾向率空间分布的预估研究时,可以考虑采用最优模式集合平均的方式进行预估.

从区域平均气温的多年变化来看(图5b),MME5所模拟的区域平均多年变化比MME6平均更接近观测数据,但其模拟的线性趋势为0.27 ℃/10a(p<0.001),略小于MME6所模拟的增温趋势0.28 ℃/10a(p<0.001),也小于观测数据(0.43 ℃/10a).与单模式的模拟结果相比,MME5与MME6的模拟结果并不占优势,均有一定程度低估,这跟筛选指标Mr有关,Mr高虽然说明模式的综合模拟能力强,但是可能会弱化了其对某单一变量的模拟能力,具体是因为MME5与MME6对区域平均气温的多年变化的S值排名靠后(分别为19名和14名),但年平均气温气候态及其气候倾向率的空间分布的S值排名都在前10名,因此Mr较高.

观测数据显示(图6a),中国东北地区年平均气温气候态空间分布整体上由北至南逐渐升高,黑龙江省最北部低温区年平均气温在-4 ℃以下,辽宁省的西南部年平均气温在6 ℃以上.MME5与MME6均能大致模拟出东北地区年平均气温由北至南逐渐升高的分布特点以及高、低温中心的分布,但普遍存在低估的现象.MME5的模拟结果中(图6b),除辽宁东部、吉林东部存在暖偏差,其余地区大部分被低估.MME6的模拟结果比MME5更接近观测值(图6c),尤其是对辽宁东部、吉林东部的暖偏差有了一定改善.

图5 1961—2005年中国东北地区CMIP5与CMIP6最优模式集合方案(MME5与MME6)模拟相对于观测 在3个角度下的泰勒图(a)与其模拟中国东北地区区域平均气温多年变化的结果(b) (a)中圆形、方形、三角形分别表示最优模式集合方案对年平均气温气候态空间分布、区域平均气温多年变化、 年平均气温气候倾向率空间分布的模拟结果.Fig.5 Taylor diagrams for the three provinces in Northeast China between the preferred models ensemble mean for CMIP5 (a, MME5)/ CMIP6 (b, MME6) and observations under 3 dimensions for the period 1961—2005(a) and interannual variations of regionally averaged surface air temperature over the three provinces in Northeast China for MME5 and MME6 during 1961—2005 (b) The circle, square and triangle characters respectively indicate spatial distributions of annual mean surface air temperature, interannual variations of regionally averaged surface air temperature and spatial distributions of annual mean surface air temperature trends in (a).

图6 1961—2005年中国东北地区观测场(a、d)与CMIP5(b、e)、CMIP6(c、f)最优模式集合方案(MME5与MME6)的 年平均气温气候态空间分布(a—c,单位：℃)及其气候倾向率空间分布(d—f,单位：℃/10a)Fig.6 Spatial distributions of annual mean surface air temperature (a—c,units=℃) and trends (d—f, units=℃/10a) of the three provinces in Northeast China over the period of 1961—2005 for the CN05.1 (a,d), CMIP5 (b,e) and CMIP6 (c,f) preferred models ensemble mean (MME5, MME6)

从气候倾向率的空间分布来看,中国东北地区均在升温,其中黑龙江省、吉林省的大部分区域气候倾向率大于0.4 ℃/10a,辽宁省的气候倾向率在0.15～0.35 ℃/10a之间(图6d).MME5与MME6的模拟结果均不理想,虽能大致模拟出东北地区的增温速率由北到南逐渐减小,但数值上普遍出现低估,尤其是在黑龙江北部低估最明显(图6e—f).

3 结论

中国东北地区对全国农业、林业与经济发展具有重要的意义(陶纯苇等, 2016),而模式作为预估未来气候的重要方法(Chen et al., 2020),越来越多地被科学界所使用,评估模式的可靠性并探讨CMIP6对中国东北地区气温的模拟是否有所进步至关重要.本文通过泰勒图、S值以及Mr,系统地评估了39个CMIP5模式和34个CMIP6模式对中国东北地区年平均气温特征的模拟能力,分析CMIP6单模式与MME6的模拟能力是否有所提高; 在此基础上,探讨了模式个数对优选模式集合平均模拟结果的影响.主要结论如下：

(1) 绝大多数CMIP6模式对中国东北地区年平均气温气候态空间分布的模拟效果最好,且模拟结果一致性较高,但对于区域平均气温的多年变化及其线性趋势存在低估.相比于CMIP5,CMIP6整体上能更好地模拟出年平均气温特征,但两代模式对年平均气温气候倾向率空间分布的模拟能力有限.从CMIP6与其在CMIP5中的早期版本比较来看,CMIP6模式对区域平均气温的多年变化、年平均气温气候态空间分布及年平均气温气候倾向率空间分布的模拟能力有所提高,改善模式个数占CMIP5与CMIP6共有模式个数的56.3%、87.5%和50%.

(2) 优选模式集合方案比所有模式的集合平均方案及大多数单模式更优,随着集合平均方案的模式个数的增加,模式的综合模拟能力呈“上升-下降”的趋势.此外,没有一个模式能够在所有情况下都表现最佳,因此,在做多模式集合平均时,模式用户需要根据自己的需要进行优选,并确定模式样本的个数.

(3) MME5与MME6均能模拟出年平均气温由南到北递减以及其趋势由南到北递增的特点.相比于MME5,MME6能更好地模拟出东北地区的年平均气温气候态空间分布及年平均气温气候倾向率空间分布,然而,MME6对区域平均气温多年变化的模拟能力要略低于MME5,这是由于筛选指标Mr会忽略模式对某单一变量的模拟能力.因此,虽然MME6的综合模拟能力较优,但MME6不能很好地模拟出东北地区区域平均气温多年变化.