一种基于WPT和LSTM的孤岛检测算法
黄文聪, 王增雯, 常雨芳, 王明辉
(1 湖北工业大学电气与电子工程学院, 湖北 武汉 430068; 2 江苏金风软件技术有限公司, 江苏 无锡 214000)
非计划孤岛是电网侧故障分布式发电机(Distributed Generator,DG)未及时离网并继续向负荷供电的一种不正常运行状态[1-2]。非计划孤岛会使电压、频率偏离正常运行范围,干扰继电保护动作时序,破坏电力系统的稳定运行状态,威胁电力检修人员生命,因此防孤岛状态装置应该迅速可靠动作[3]。根据IEEE标准1547-2018,防孤岛装置动作时间应当限制在2 s以内[4]。
孤岛检测通常分为主动检测法(有源法,Active Islanding Detection Method,A-IDM)、被动检测法(无源法,Passive Islanding Detection Method,PIDM)和混合检测法(Hybrid Islanding Detection Method,H-IDM)[2]。主动检测法是改变逆变器输入信号进而改变逆变器的输出值,同时监测系统状态量的变化来检测孤岛的方法[5-8]。被动检测法是通过监测电压和电流的幅值、频率、相位及其谐波含量等指标来检测孤岛的方法[9-12]。智能检测法,也称为混合检测法,是将被动检测法与智能算法相结合的一种较新的孤岛检测方法[13-16]。文献[17]提出一种改进的频率正反馈无功电流扰动的孤岛检测方法,通过周期性地施加无功扰动电流使频率越限进而实现防孤岛效应的功能,在孤岛发生时,能够加速频率偏移,缩小检测盲区,但该方法依然给电网增加了扰动,影响电能质量。文献[18]对多机并联情况下应用频移式孤岛检测法时正反馈增益与采用频移法逆变器比例的关系,表明正反馈增益必须根据逆变器并联数量的比例同步增大,但增大反馈增益也会增加谐波干扰,导致电能质量下降。文献[19]提出一种基于小波包能量熵和BP神经网络相结合的孤岛检测法,弥补传统的孤岛检测算法需要设置阈值的问题,将电压、电流信号合成一个多维特征向量,降低网络的输入维度,减小网络的计算量,但未考虑到低次和高次谐波干扰,检测准确率不高。
针对现有的智能孤岛检测方法的不足,提出一种基于db3小波包重构算法与长短时记忆(Long Short-Term Memory,LSTM)神经网络相结合的智能孤岛检测算法。对公共耦合点处的电压信号进行采样;将小波包变换分解的多层信号进行重构,重构信号包含8-40次倍频的孤岛谐波成分,舍弃1-7次的低频信号成分和40次以上的高频谐波成分,避免高频信号混叠。最后,利用长短期记忆神经网络对输入网络的高频孤岛特征进行分类识别,提高孤岛检测的准确率和检测速度。
1 非计划孤岛检测方法
所提出的非计划孤岛检测方法,在小波变换理论的基础上,结合LSTM神经网络对孤岛波形进行特征提取分类,并判断孤岛和非孤岛两种运行状态。若判别为孤岛情况,则动作于断路器跳闸。波形分类训练流程见图1。
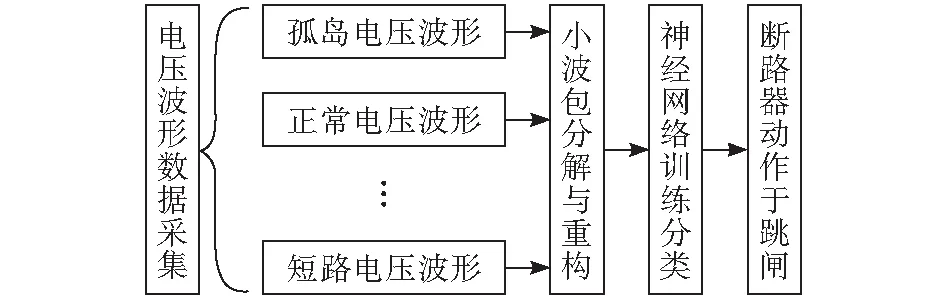
图1 LSTM 神经网络训练分类流程
1.1 小波包变换原理
从公共耦合点提取的电压波形包含基波和不同次数的谐波。电压波形数据集的预处理选用了经典的小波包变换算法。小波包变换可通过其系数幅值表现信号的不规则性,且小波包变换特别擅长处理非线性信号,弥补了传统的傅里叶变换只能分析近似周期性的波动信号的缺陷。
小波包变换的母小波既可以沿着时间轴前后平移,又可以按比例伸展和压缩以获取高频和低频小波,相当于高通滤波器和低通滤波器的组合。小波包变换具有良好的时频特性,可以将信号分解到时频域表示,并能保证频率范围内有良好的时间分辨率和频率分辨率。母小波ψa,b(t)是构建小波变换的窗函数,其归一化的基本小波即母小波函数可以紧凑地写成如下形式:
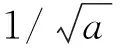
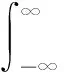
小波母函数ψ(t)的中心和半径分别用t*和Δψ表示,则ψa,b(t)的中心为b+at*,半径为aΔψ,计算公式如下:
式中‖ψ(t)‖2为ψ(t)的范数,ψ(t)的时间窗tω=[b+at*-aΔψ,b+at*+aΔψ]。由于ψ(t)具有衰减特性,时间窗外的信号部分可以忽略不计。
连续时域信号x(t)的积分小波变换在数学上可以表示为
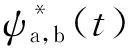
小波变换是可以进行逆变换的,将连续信号进行小波分解后对其进行重构,该过程满足公式
通过上述步骤,即可完成对时域信号x(t)的分解和重构。
1.2 电压波形小波包分解与重构
小波变换非常适合处理瞬态的信号,即频率和幅值同时变化的信号。母小波的选择是至关重要的。所提方法选用的是3阶Daubechies小波。通过使用对比各种小波分解和重构,从分类效果可知使用3阶Daubechies小波能够有效提取孤岛波形处理,使其重构的低频信号代表电压波形的主成分,而重构的高频信号则能体现孤岛特征。
由图2可知,使用小波包分解信号的过程相当于将原始电压信号的低频成分和高频成分进行滤波处理,即第一层(1,1)为原始信号S的低频成分,(1,2)为原始信号S的高频成分,第二层(2,1)为第一层信号(1,1)的低频成分,(2,2)为第一层信号(1,1)的高频成分,(2,3)为第一层信号(1,2)的高频成分,(2,4)为第一层信号(1,2)的高频成分,以此类推。

图2 小波变换包波形分解
需进行预处理的电压信号采样频率5 kHz,根据香农采样定理,最高采样频率为2.5 kHz,当分解的信号接近2.5 kHz时,不能准确分辨该高频信号的频率。对小波包分解系数进行重构时,为避免低次和高次谐波干扰,影响电压波形中孤岛特征的表达和提取,选择滤掉部分低频和高频成分的系数进行重构,即选择(4,2)和(4,15)之间所有成分,舍弃(4,1)和(4,16)这两个分量,重构的示意图见图3。
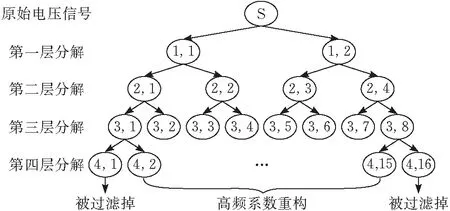
图3 小波高频系数重构信号流程
通过对电压波形进行小波包分解与重构,完成了对输入信号的预处理。为验证小波包重构后的电压中无谐波干扰,对重构的信号进行频谱分析,得到图4所示的频谱能量图。

图4 小波分解再重构的信号频谱
3-7次谐波对电网的影响不可小觑,电网中的滤波设备会将3-7次谐波降到最低,为避免基波与3-7次谐波干扰,通过小波重构得到的高频信号已将其滤除,此外,为了防止高频信号的混叠,40次以上的谐波成分也被过滤掉。由图4可以看出,重构的高频信号的频率范围约在480-2400Hz之间,即在基波的8-40次谐波范围内,因而可将此重构的波形数据作为神经网络的输入进行下一步的特征提取与分类。
2 LSTM神经网络设计
将电压波形进行小波分解和重构后的信号含有大量的孤岛特征,更易于计算和判别,因此需要选择一个可靠适用的神经网络来进行训练学习并判断孤岛。传统的BP神经网络训练过程复杂,无记忆能力,孤岛检测准确率最高为96%。为改善孤岛检测算法性能,孤岛波形的训练及分类采用了经典的LSTM神经网络的结构。LSTM神经网络不必记忆输入信号所有特征,只选择记忆有用的特征信息,可减轻记忆负担,同时提高网络分类准确率。在识别孤岛特征时,能够准确提出孤岛特征,适应数据集的变化,判别孤岛和非孤岛的情况。
LSTM神经网络采用4层结构,包括输入层(input layer)、两层隐含层(hidden layer)和输出层(output layer)。孤岛检测算法采用的神经网络结构见图5。
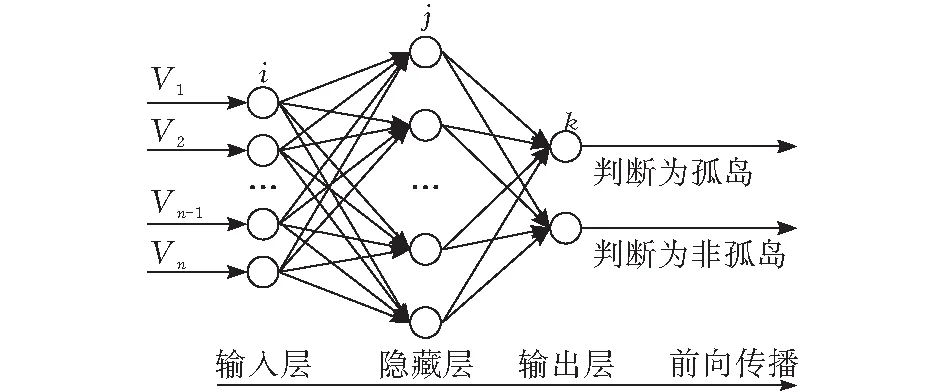
图5 LSTM神经网络模型训练迭代图解
LSTM神经网络输入层的数据是将原始的电压波形信号经过小波变换得到的,滤除了基波及其低次谐波成分,是一个1行400列的数据,因此神经网络的输入层为400个神经元。隐含层神经元的数目主要影响的是均方误差和训练速度,选取过大和过小都不利于网络的学习和正确分类。经过验证,隐含层选用2层的结构,第一层隐藏层含20个神经元,第二层隐藏层含13个神经元。最后,输出层是为了判断输入是否为孤岛的情况,因此只需两个神经元即可。在电压波形数据集中,孤岛波形的标签为1,非孤岛波形的标签为0,则网络输出为1则代表属于孤岛情况,输出为0则代表非孤岛情况。
训练流程框图见图6。

图6 LSTM神经网络模型流程
为了保证网络训练结果的可靠性,训练数据和测试数据之比为7∶3。神经网络的反向传播过程就是使用梯度下降法原理,对权重和偏置进行更新,逐步找到成本函数的最小值,得到最终的模型参数。模型训练的速度取决于学习率的设置,为保证训练的速度和准确度,将学习率设置为0.0002。
3 孤岛效应PSCAD建模仿真
分布式光伏电站并网时,公共耦合点的电压电流信号经锁相环将相位信号送至虚拟同步发电机,脉冲发生器发出控制信号,控制分布式光伏电站逆变器的输出,使光伏电站输出电压的相位同步。光伏电站发电方式采用基于扰动观测法的最大功率点跟踪算法,光伏电站并网逻辑见图7。
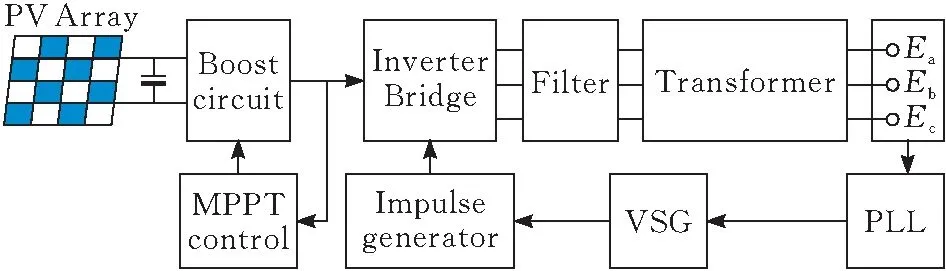
图7 分布式光伏电站并网逻辑结构
以美国某分布式光伏电站并网系统为例,遵照并网逻辑对分布式光伏电站进行建模,使用一个容量为100 MVA 60Hz的交流发电机模型来代替传统的大电网,25 MVA的分布式光伏电站并网,使其能够同时为光伏侧的负载1和电网侧的负载2供电。随机断开并网断路器,并记录离网前后负载侧的电压波形数据,即为孤岛发生的波形数据。系统仿真见图8。
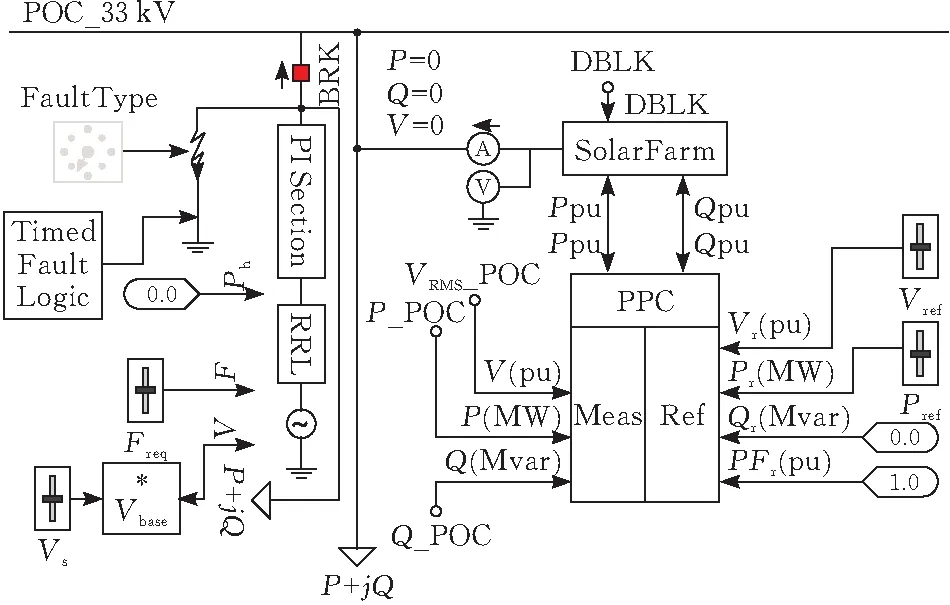
图8 分布式光伏电站PSCAD并网建模仿真
如图8所示,当断路器BKR断开后,右侧的光伏电站和本地负载形成电力孤岛,通过公共耦合点PCC电压波形进行采集,得到孤岛波形数据。另外,在交流发电机侧添加故障元件,模拟电网故障,同时对PCC处电压波形进行采集,得到区别于非孤岛情况下的各种故障波形数据。美国该分布式光伏电站参数见表1。

表1 美国某分布式电站参数
电压波形数据集由三类不同工况下的电压波形构成,电压波形数据是从公共耦合点处采集的,包括正常电压波形、短路电压波形和孤岛电压波形。正常电压波形采集的时间点随机确定,共包含120组数据。短路电压波形是模拟各种短路故障获得的,包含单相接地波形、两相短路波形、两相接地短路波形和三相短路波形,共有13组数据。孤岛电压波形共包含120组数据,采集的时间点也是随机确定的,且光伏侧负载大小也是随机的,保证了实验结果的可靠性。
4 孤岛检测算法评价
为了检验不同孤岛检测算法的效果,引用混合矩阵(Confusion Matrix)来检验基于不同小波的检测算法的性能。混合矩阵中的TP(The Number of True Positive Cases)代表真阳性事件的数量,即实际为孤岛事件的数量,FN(The Number of False Negative Cases)代表假阴性事件的数量,即被误认为是非孤岛实则属于孤岛事件的数量,TN(The Number of True Negative Cases)代表真阴性事件的数量,即实际为非孤岛事件的数量,FP(The Number of False Positive Cases)代表假阳性事件的数量,即被误认为是孤岛实则属于非孤岛事件的数量。运用混合矩阵对基于db3小波的智能孤岛检测方法进行评价的结果见表2。
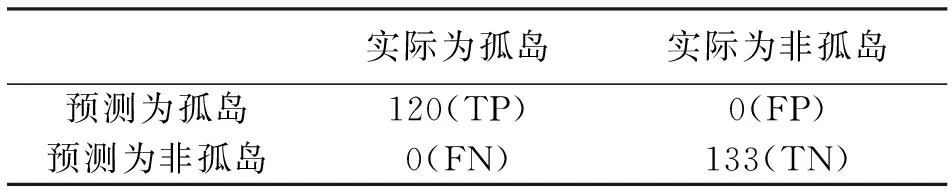
表2 孤岛检测结果的混合矩阵
从实验结果来看,基于db3小波变换的智能孤岛检测方法能够准确地识别孤岛和非孤岛两种,假阳性率和假阴性率都为0。由表3可得,基于小波的智能孤岛检测算法能够准确识别孤岛情况,而基于db3小波的智能孤岛检测算法优于基于其他小波基的处理效果,迭代次数少,仅迭代了10次,能够减少计算时间和计算量,同时也能更快地检测到孤岛情况的发生。迭代准确率变化曲线见图9。由图9可知,基于db3的智能孤岛检测算法的准确率可随迭代次数的增加迅速提高,检测速度更快。
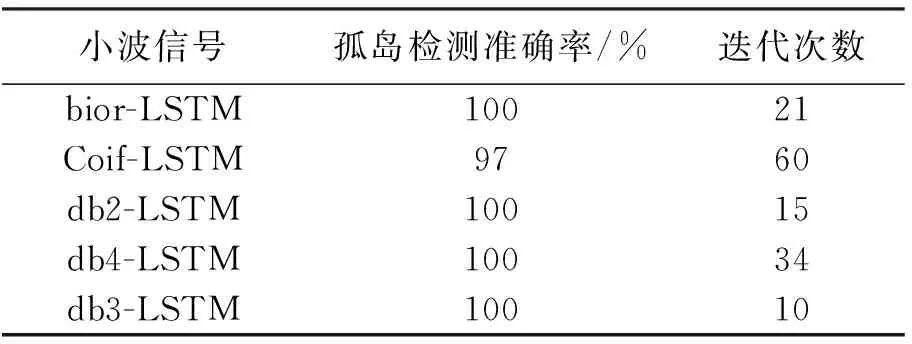
表3 基于不同小波的孤岛检测方法对比
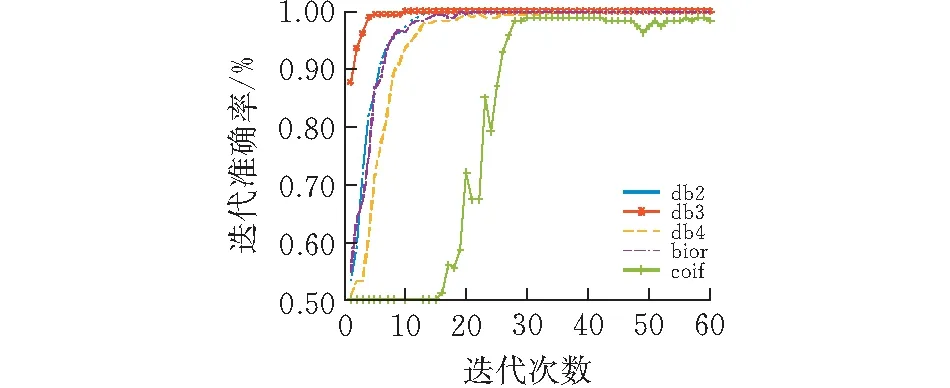
图9 孤岛检测准确率迭代变化曲线
用该法对非孤岛情况识别的效果进行验证,检测结果见表4。
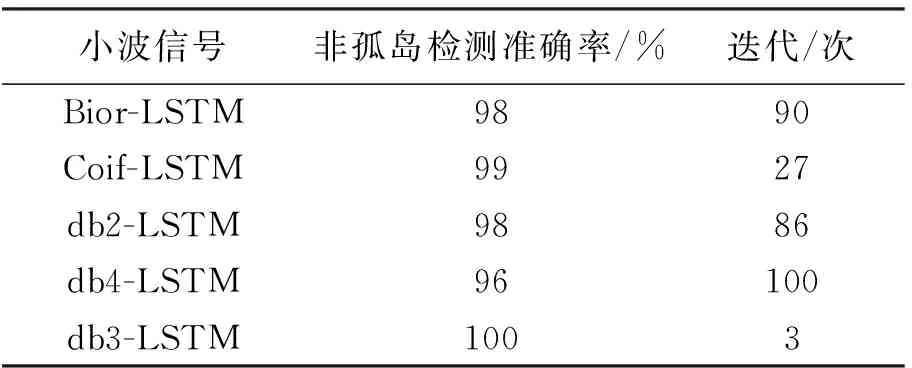
表4 基于不同小波的非孤岛检测方法对比
由表4可得,除db3以外的其他小波都不能够完全识别非孤岛的情况,假阳率均不为0,而基于db3小波的智能孤岛检测算法也能够正确识别分类非孤岛情况,假阴性率为0,算法性能优于其他处理效果,且迭代次数最少,迭代准确率变化见图10。
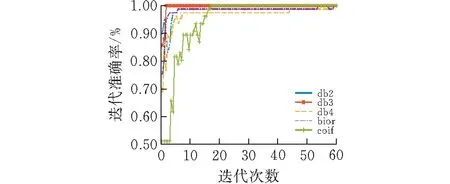
图10 非孤岛检测准确率迭代变化曲线
综上,基于db3小波的孤岛检测算法能够准确将孤岛和非孤岛的运行情况准确识别,假阳性率和假阴性率均为0,且迭代次数少,计算时间短。相较于传统的利用过频/过压来进行孤岛检测的方法,基于db3小波的孤岛检测算法检测盲区几乎为0,且不需要设置固定的跳闸阈值且检测时间较短,非孤岛检测准确率高,即误动作概率小,满足分布式电站孤岛检测需求。
5 结论
对比结果表明,3阶Daubechies小波分解重构方法与LSTM神经网络结合的孤岛检测算法优于传统的智能检测算法,得到的结论如下:
1)所提孤岛检测算法具有拓扑自适应性,弥补了电压/低电压(OUV)和过频/低频(OUF)检测需要设置阈值的缺陷,在功率匹配的运行工况下,仍具有孤岛检测能力;
2)利用小波变换对电压波形进行处理,能够捕捉谐波中的高频孤岛特征,提高神经网络对孤岛分类的准确率;
3)在相同的神经网络结构下,基于3阶Daubechies小波孤岛检测的效果优于基于其他小波处理的检测效果,检测准确率较高。

