侧壁角对梯形琴键堰泄流能力的影响
袁 柳,吉庆丰
(扬州大学 水利科学与工程学院,江苏 扬州 225009)
1 研究背景
随着越来越多的水库对蓄水需求的增加,以及对大坝安全的要求越来越高,部分溢洪道的泄流能力不能满足实际需求,需要寻找措施来解决过流的要求。通常采取增加溢洪道宽度、降低溢洪道顶部高程、用其他堰型代替现有的直线堰等措施。然而,增加溢洪道宽度会受到地形条件的限制,降低溢洪道顶部高程则需要在堰顶增设控制建筑物,如闸门等,带来运营管理成本,经济性不高。
琴键堰(P.K堰)最早由法国人Lempérière等[1]发明,它是迷宫堰的进一步发展,将迷宫堰的宫室向上下游悬挑,不仅可以保持迷宫堰原有的堰顶长度,还可以减小基础面积,从而减少建筑成本,克服了迷宫堰的不足。近些年,Pfister等[2]、Ribeiro等[3]对P.K堰的水力设计进行了研究。国内李珊珊等[4]、姜铎等[5]分别研究了堰高和上下游倒悬比对过流能力的影响。祁媛媛等[6]将数值模拟结果与试验结果进行对比,论证了数值模拟的合理性。Machiels等[7]通过试验研究了P.K堰的流动特征。而李国栋等[8]利用数值模拟的优点研究了不同溢流前缘的水流特性。Ribeiro等[3]、Kabiri-Samani等[9]、郭新蕾等[10]和胡晗等[11]拟合了P.K堰的流量系数。Karaeren等[12]、Anderson等[13]比较P.K堰和迷宫堰的水力性能,认为P.K堰的性能更为优越。
尽管人们对P.K堰进行了大量研究,但很少有人去研究梯形琴键堰(T.P.K堰),Safarzadeh等[14]依据梯形迷宫堰的设想,尝试改变侧壁角,将T.P.K堰、P.K堰和迷宫堰3种堰进行对比,从而得出了T.P.K堰可能拥有更高过流能力的结论。但他并没有专门对侧壁角进行研究。
本文在不改变泄槽宽度的情况下,仅改变侧壁角,研究不同侧壁角对T.P.K堰过流能力的影响,并且利用数值模拟的优点,对不同溢流前缘进行监控,同时通过流态、流速等解释侧壁角对过流能力的内在影响原因。
2 T.P.K堰的模型构建与网格划分
2.1 T.P.K堰的几何参数与模型建立
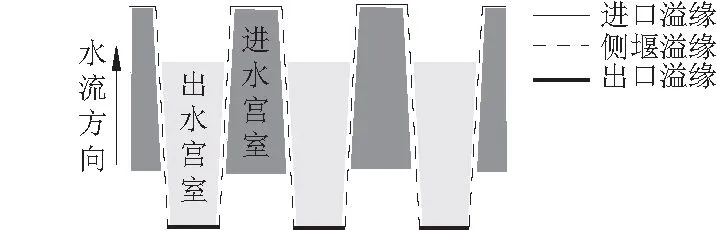
T.P.K堰的结构十分复杂,如图1、图2所示。T.P.K堰的几何参数有:进水宫室上、下游宽度Wiu、Wid;出水宫室上、下游宽度Wou、Wod;T.P.K堰堰单元宽度Wu;泄槽总宽度即堰宽W;进口倒悬长度Bi;出口倒悬长度Bo;基座长度Bb;堰长B=Bi+Bo+Bb;壁厚Ts;侧壁与主流方向的夹角即侧壁角α;T.P.K堰堰高P;T.P.K堰堰以下高度Pd;进水宫室坡度Si;出水宫室坡度So。T.P.K堰单元是T.P.K堰的基本结构,一个T.P.K堰单元由一个进水宫室、两个侧堰、两个半出水宫室组成。
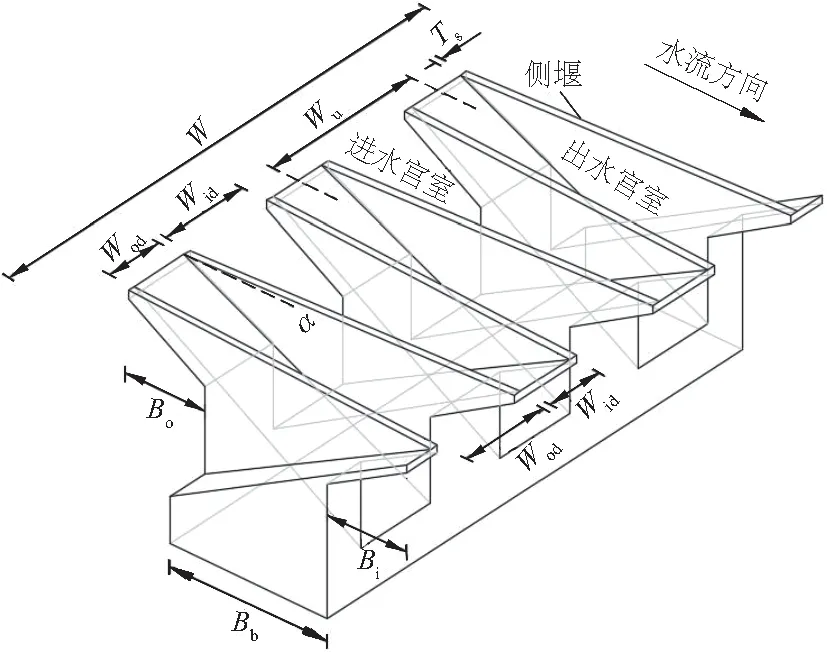
图1 T.P.K堰结构示意图Fig.1 Structure of trapezoidal piano key (TPK) weir

图2 T.P.K堰剖面图Fig.2 Profile of TPK weir
为了研究不同侧壁角对泄流能力的影响,本文采用5组不同的侧壁角,泄槽总宽度为0.39 m。保证相同的堰高、堰宽和堰长。Lempérière把进、出口倒悬长度相等的堰型称作对称A型T.P.K堰,其具有结构稳定的优点,故设置Bo/Bi=1。而Wou/Wid=1也是最基本的体型结构参数。具体尺寸如表1所示。其中,L为T.P.K堰的溢缘总长,L的改变是由于堰长和堰宽一定时,增大侧壁角会挤压进、出口溢缘,而侧堰溢缘的长度却拉伸得很少,从而使L减小。
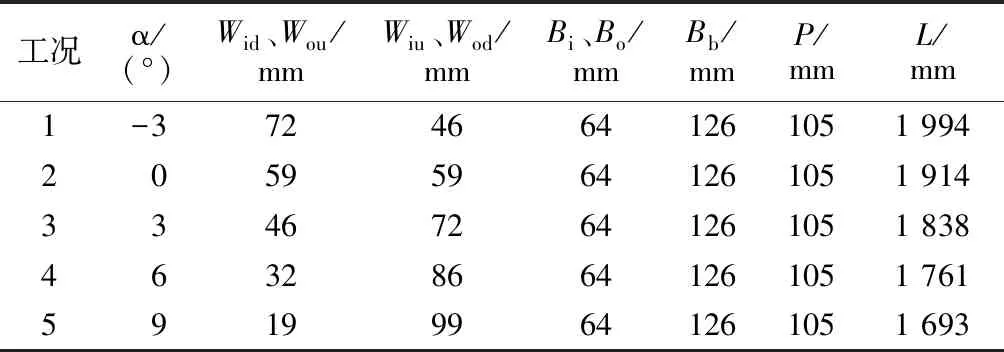
表1 T.P.K堰模型几何尺寸
2.2 网格划分
计算区域如图3所示,为了使水流稳定,上游行进段设置为4 m,下游设置为2 m。整个区域的网格划分在ICEM软件里进行,在T.P.K堰段,由于区域的复杂性,选择四面体非结构网格,即网格一。网格二选择均匀的六面体结构化网格,堰体局部网格如图4所示,网格总数约为3.2×106。
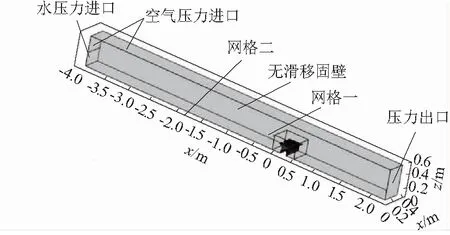
图3 T.P.K堰计算模型Fig.3 Calculation model of TPK weir

图4 堰体局部网格Fig.4 Local grids of weir body
3 数学模型及边界条件
3.1 湍流模型
本文选用RNGk-ε模型,该模型通过在大尺度运动和修正后的黏度项中体现小尺度的影响,而使这些小尺度运动系统地从控制方程中去除,所得的输运方程为:
ρε-YM+Sk;
(1)
(2)
式中:Gk为平均速度梯度引起的湍动能产生项;Gb为浮力引起的湍动能k的产生项;YM表示可压缩湍流中脉动扩张的贡献;C1ε、C2ε和C3ε为经验常数;αk和αε分别为与湍动能k和耗散率ε对应的Prandtl数;Sk和Sε是用户定义的源项;ρ为密度;t为时间;ui为xi方向上的速度分量;uj为xj方向上的速度分量;μeff为湍流粘性系数;Rε为方程附加项。
3.2 自由水面处理
T.P.K堰的水流属于带有自由表面的水流流动,采用VOF法对该复杂自由水面进行处理,通过求解动量方程和体积分数的方法来模拟多种互不混掺的流体运动。在VOF法中,不同的流体共用一套动量方程,通过引进体积分数这一变量,实现对每一个计算单元相界面的追踪,其中水和气不发生质量交换,具有相同的速度和压力场。在VOF法中,追踪第m相流体自由水面的控制微分方程为
(3)
式中:αm为水的体积分数;t为时间;ui和xi分别为速度分量和坐标分量(i=1,2,3)。
3.3 边界条件
如图3所示,入口边界由水压力进口和空气压力进口组成,均为压力进口边界;出口为自由出流,设为压力出口边界,墙壁为无滑移边界条件。湍流参数k、ε采用经验公式计算,即:
k=0.003 75u2;
(4)
ε=k1.5/(0.4h) 。
(5)
式中:u为进口流速;h为T.P.K堰堰上水头。
3.4 模型验证
本文采用Kumar等[15]的试验数据进行模型验证(P.K堰,即α=0°),采用的模型尺寸与试验一致,共设有10种不同的水头条件,用H/P表示,H包含堰上水头和行进流速水头,即H/P=0.102、0.208、0.354、0.490、0.626、0.775、0.860、0.935、1.061、1.197。通过和试验结果的比较发现(图5),数值计算结果的平均相对误差为3.04%。当水头极低(H/P=0.102)时,最大相对误差为7.10%,其余相对误差都在5%以内,证明采用数值模拟的计算结果是可靠的。
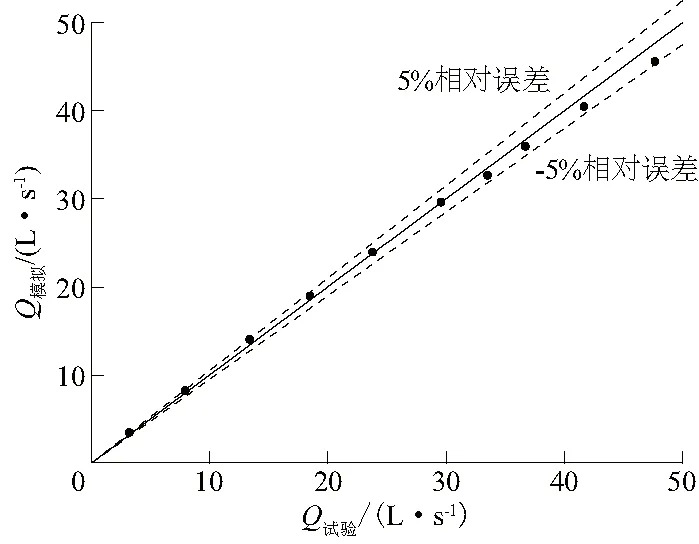
图5 模拟流量与试验流量比较Fig.5 Comparison between simulated discharge and experimental discharge
4 T.P.K堰泄流能力
4.1 总泄流能力
经过数值模拟计算,可以得出T.P.K堰不同侧壁角的总泄流量(表2),结果表明α=-3°时,T.P.K堰的部分泄流能力不如P.K堰(α=0°),而α=6°和α=9°对应的泄流量相对较高。
为了验证T.P.K堰具有超强的泄流能力,Leite Ribeiro等[3]提出超泄比r,即用T.P.K堰的泄流量除以对应情况下等宽薄壁堰的泄流量,薄壁堰的流量公式为
(6)
式中:h为堰上水头;g为重力加速度。
流量系数m用雷卜克公式计算,即
m=0.407+0.053 3h/P。
(7)
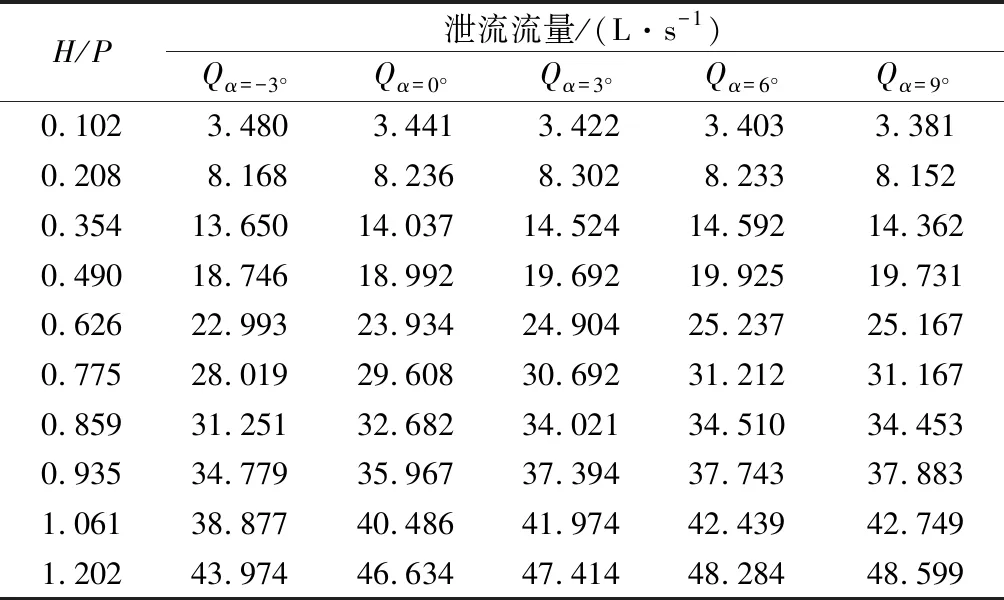
表2 T.P.K堰不同侧壁角的泄流流量统计结果
如图6所示,当水头很低(H/P=0.102)时,T.P.K堰的泄流量是等宽薄壁堰泄流量的4.5倍左右,效率最高,不同侧壁角的超泄比相差不大。随着水头的增加,超泄比下降。当H/P=0.490时,超泄比已下降为2.5左右,衰减的速度较快,不同侧壁角对应的超泄比也逐渐产生差异。其后,水头继续增加,超泄比的下降也趋于缓慢,泄流量只有普通薄壁堰的1.5倍,不同侧壁角之间的泄流量差异也变得更为明显。
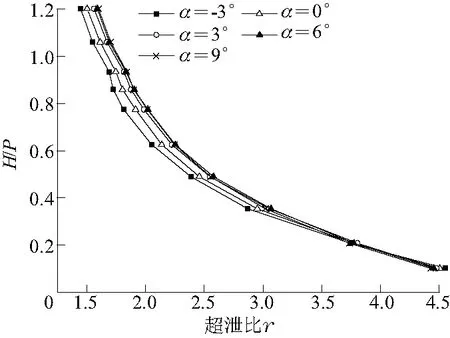
图6 不同侧壁角超泄比与堰上相对水头关系Fig.6 Relations between discharge amplification ratio and H/P with different side wall angles
为了比较改变侧壁角带来的的流量差异,将以α=0°的流量作为参考,绘制不同侧壁角下流量相对增长百分数与相对水头的关系图(图7)。当侧壁角为负数时,在水头很低(H/P=0.102)时,泄流能力比P.K堰高出0.5%,其余泄流能力都不如P.K堰,当H/P=1.197,α=-3°的泄流量比P.K堰的泄流量低出5.7%,说明侧壁角为负数,对泄流能力产生不利影响。当侧壁角为正数时,在低水头(H/P=0.102),T.P.K堰的泄流量低于P.K堰泄流量,随着水头的升高(0.208 图7 不同侧壁角流量相对增长百分数与堰上相对水头关系Fig.7 Relations between relative growth percentage of flow and H/P with different side wall angles 如图8所示,流经T.P.K堰的水流可看作由进、出口溢缘,侧堰溢缘3部分流出的水流组成。在数值模拟中利用面积分的方法,可以分别积分计算通过T.P.K堰3部分溢流前缘上的泄流量,从而可以更细致地研究不同侧壁角对T.P.K堰的影响。 图8 T.P.K堰各溢流前缘 (α=3°)Fig.8 Front overflow edges of TPK weir(α=3°) 绘制不同侧壁角下各溢流前缘泄流量占总流量百分数图,可以得到各溢流断面在泄流过程中所占的比重。 由图9可知,随着相对水头的升高,流经进、出口溢缘流量占总流量的比重上升,流经侧堰溢缘的水流占总流量比重呈下降趋势。由图9(a)、图9(b)可知,不同侧壁角对流经进、出口溢缘的流量百分数影响类似。都为在α=-3°时,流经进、出口溢流前缘的水流比重最多,α=9°时,流经进、出口溢流前缘的水流比重最小。并且随着水头的增加,α=-3°流经进、出口溢缘的百分数增加幅度较大,而α=9°则相反。这说明侧壁角的增大使流经进、出口水流的比重减少,并且随着水头的增加,减少的越多。 由图9(c)可知,与进、出口溢缘相比,侧堰泄流流量在整个泄流过程中所占的比例最高,最高占比为90.36%,随着侧壁角的增大,流经侧堰的水流占比也越大,当α=9°时,侧堰百分比都维持在较高水平。同时侧壁角的增大,侧堰百分比随相对水头升高的变化幅度逐渐减小。 图9 不同侧壁角下各溢流前缘泄流量所占百分比Fig.9 Curves of the percentage of overflow front discharge flow with different side wall angles 用各溢流前缘的泄流量除以等宽薄壁堰的泄流量可以评估各溢流前缘的泄流效率。如图10所示,各溢缘的泄流效率都随相对水头的增加在减小,其中侧堰出流的泄流效率减小幅度较为迅速,减小幅度在65.5%~78.1%之间。由图10(a)可知,在水头极高或极低的情况下,不同侧壁角会对进口泄流效率产生差异,其他水头条件下变化不大。由图10(b)可知,不同侧壁角的出口效率相差也很小,α=9°的出口效率略小于其他侧壁角的出口效率,但随着水头的增加,差距在逐渐减小。由图10(c)可知,α=9°的侧堰泄流效率最高,并且侧壁角越大,对应的侧堰泄流效率越高。随着相对水头的增加,不同侧壁角的侧堰泄流效率差距也逐渐增大。总之,侧堰泄流效率是影响不同侧壁角泄流能力的主要原因。 图10 不同侧壁角下各溢流前缘泄流效率Fig.10 Efficiency of overflow front discharge with different side wall angles 对T.P.K堰的流动特性进行研究,可以进一步阐释不同侧壁角带来的影响。 由图11(a)可知,对于低水头情况,T.P.K堰的进水宫室表面轮廓非常平坦,进入出口宫室的水流沿着出口宫室倒悬坡度自由下泄。图11(b)为T.P.K堰的三维流场,显示水流大概运动轨迹,底层水流主要从进口宫室流出,中部水流从侧堰出口流出,表层水流一部分从出口直接留出,另一部分则通过侧堰向下游排泄。由于相对水头较低,在出口宫室的3股水流挑距很小,水流之间不会相互影响,各溢缘类似于展开的等宽薄壁堰,水流都处于自由溢流的状态,这也是低水头时整体泄流效率较高的原因。 图11 T.P.K堰流态图和三维流场(H/P=0.102,α=3°)Fig.11 Flow pattern and three-dimensional streamlines of TPK weir (H/P=0.102,α=3°) 对于中高水头,表层水流经过侧堰后,在出水宫室交叉碰撞,形成堵塞,如图12(a)所示。随后出水宫室被淹没,阻碍了水流的通过。随着侧壁角增大,出口宫室逐渐扩张,如图12(b)、图12(c)所示,流经侧堰的两股水流逐渐分开,两股水流的冲击的高度也随之下降,降低了两股水流的干扰程度,使流经侧堰的水流顺利下泄,从而提高了侧堰的泄流效率,增加了T.P.K堰的泄流能力。 同时,部分中层水流也会进入出水宫室,加剧堰的堵塞。由图13可知,大量的水流从进水宫室涌入,在进水宫室坡度Si的作用下,水流沿着进口宫室逐渐抬升,进水宫室所能容纳的流量逐渐减小,到了进水宫室的尾端,允许通过的流量十分有限,只有少 图12 3种不同工况出口宫室横剖面水流流态 (H/P=0.860)Fig.12 Flow regime at horizontal profiles of the exit chamber under three conditions (H/P=0.860) 图13 3种不同工况出口宫室纵剖面水流流态 (H/P=0.860)Fig.13 Flow regime at vertical profiles of the exit chamber under three conditions (H/P=0.860) 部分的水流能从进口溢缘流出,此时这些水流只能从侧堰流出,增加侧堰的负担。 侧堰在T.P.K堰的流动过程中扮演着重要的作用,侧堰的效率极大地影响着T.P.K堰的过流能力。图14为T.P.K堰的中等深度的水流在侧堰上的分布。不同的侧壁角在侧堰上的水流分布不同,随着侧壁角的增加,中层水流在侧堰上流经更宽的溢缘(即Lα=9° 图14 3种工况中层流线(H/P=0.490)Fig.14 Mid level streamlines under three conditions (H/P=0.490) 图15显示了3种不同T.P.K堰的近水面层流线,不同侧壁角的表层流线在侧堰上差异比较明显,α=-3° 的T.P.K堰在侧堰的后端没有表面流线,随着侧壁角的增加,侧堰上的表面流线逐渐增多,并且表面流线在侧堰上的分布更均匀。而侧堰又占整个泄流比例最大,所以这些水流特征提高了T.P.K堰侧堰的泄流效率。 图15 3种工况表层流线(H/P=0.490)Fig.15 Surface streamlines under three conditions (H/P=0.490) 在近水层,T.P.K堰的侧堰出流类似于斜侧堰,Borghei等[16]、Ura等[17]对这种类型的斜侧堰进行了研究,认为斜侧堰的流量系数与导流角θ有关(图15)。对于α>0°,α=9°对应的斜侧堰拥有的流量系数最高,并且拥有的斜侧堰长度更长。尽管α=-3°也对应着另一种情况的斜侧堰,但是在这种情况下,T.P.K堰的出口宫室末端更易形成拥堵,抬高了末端水位,导致表层水流向出口宫室前端移动挤压,在侧堰上形成了不良的水流条件。 不同侧壁角对应的进水宫室形状也不尽相同,尽管只有一小部分水流从进口溢缘流出,但还有大部分水流首先进入进水宫室,再通过侧堰流向出水宫室,所以进水宫室里的水流条件也对T.P.K堰的泄流能力产生重要影响。 图16为进水宫室上游悬伸处中层深度的x方向速度云图和速度矢量图。发现随着侧壁角的增加,进入进水宫室的水流面积增大,进而减小了水流流入进水宫室速度,降低了水流的流动惯性,为流经侧堰的水流提供更好的水流条件。 图16 不同侧壁角进口速度分布(H/P=0.490)Fig.16 Distribution of inlet velocity with different sidewall angles (H/P=0.490) 如图16(a)、16(b)所示,侧壁附近出现负速度,形成了一个小型的回流区,回流区的存在减少了水流流经进水宫室的有效宽度,并且导致了流线的集中,阻碍了水流的流动,对水流结构不利。如图16(c)、16(d)所示,随着侧壁角的增加,回流区逐渐消失,使进入进水宫室的速度分布变得均匀,有利于水流的流动。 虽然增大侧壁角会改善T.P.K堰的水流流态,但正如表2所示,并不是越大的侧壁角对应的泄流流量越大,因为在增加侧壁角的同时,会损失进、出口溢流前缘的长度,与P.K堰相比,α=6°的进、出口溢缘长度就已经减少了近一半,损失的长度为侧壁角的正切值与堰长的乘积,从而解释了低水头各侧壁角少许流量差异的原因。同时,无论水头的高低,进、出口溢缘的泄流效率远远高于侧堰的泄流效率,所以无限扩大侧壁角是不可取的。 本文通过三维数值模拟研究不同侧壁角对T.P.K堰泄流能力的影响,对比分析了T.P.K堰的流量、流态、流速等水力特性,结果表明:α=-3°的泄流能力相对较弱,增加侧壁角会使T.P.K堰的泄流能力得到提升,并且在相对水头不是很高时,α=6°的泄流能力最强。通过研究进口、出口、侧堰上的流量百分数、泄流效率,发现流经侧堰的水流比例最大,并且侧堰效率是影响T.P.K堰泄流能力的主要因素。随着侧壁角的增大,流经侧堰的水流所占比例逐渐增加,同时,侧堰的泄流效率越高。 从流动结构上看,对于低水头,流线均匀的分布在T.P.K堰的各个溢缘,且均为自由出流状态,水流之间互不干扰,总体泄流效率很高,并且不同侧壁角之间的差异不大。对于中高水头,增加侧壁角会使出口键逐渐张开,流经侧堰水流交叉碰撞的位置逐渐降低,减少了出水宫室的堵塞,使水流顺利下泄。同时侧壁角的增加会使中、表层水流在侧堰上分布增多并且均匀。并且侧壁角的增加会使T.P.K堰的侧堰倾斜,水流形式类似于经过斜侧堰,进一步增加T.P.K堰的泄流能力。 由于进、出水宫室的俯视平面为梯形,所以侧壁角的增加使水流进入进水宫室的面积增加,降低了入口流速,减小了水流的流动惯性,为T.P.K堰的侧堰提供更好的水流条件。再有,侧壁角的增大会使进水宫室的回流区消失,增加了有效的入口宽度,从而改善水流流态。但无限增加侧壁角会带来进、出口溢缘长度的损失,同样也会减小T.P.K堰的泄流能力。经过比较得出:α=6°是一个合适的侧壁角度,能满足大多数水头条件下泄流能力较强的要求。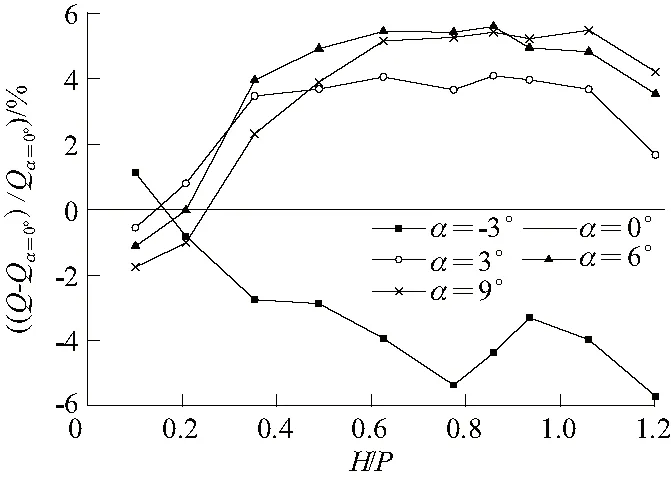
4.2 各溢流前缘泄流能力分析
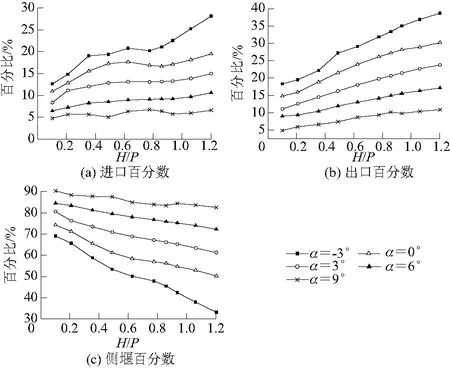
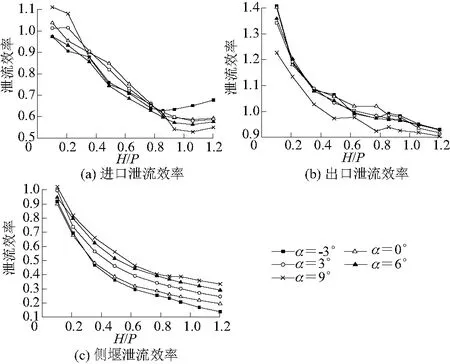
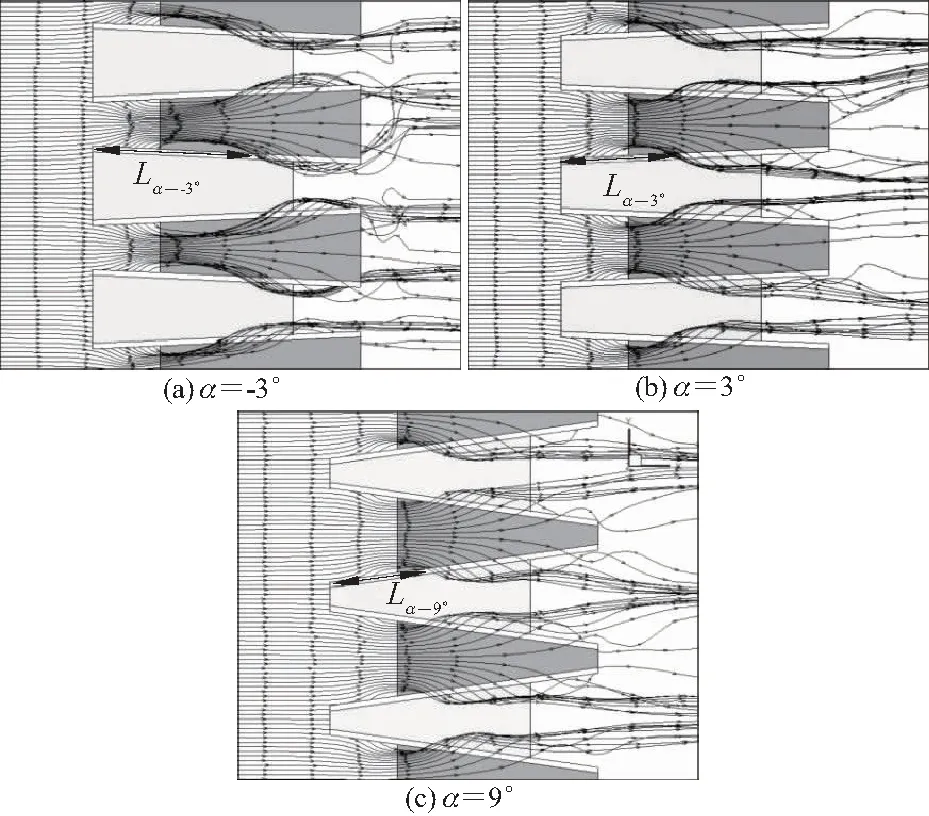
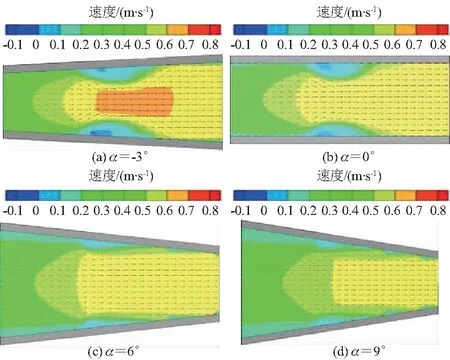
5 流动特性




6 结 论

