管道流体粗颗粒水力输送的研究进展

赵亮亮，来志强，王仲梅，王丽梅，潘丽

（1.华北水利水电大学土木与交通学院，河南郑州 450045；2.黄河水利委员会黄河水利科学研究院，河南郑州 450099；3.水利部黄河下游河道与河口治理重点实验室，河南郑州 450046；4.河南省黄河流域生态环境保护与修复重点实验室，河南郑州 450008）

0 引言

近年来管道输送在工程领域应用范围越来越广，例如水库清淤管道排沙、河流湖泊疏浚工程、深海及陆地矿石管道长距离输送等。管道输送由于其运行成本低、环境友好、受气候影响小等优点，已成为继铁路、公路、航空、水运之后第五大运输方式［1］。

就水库而言，中国20 世纪建设的许多中小型水库，由于其没有布置完善的排沙系统，水库泥沙淤积问题十分突出，需通过人工清淤以改善水库的使用功能和生命健康。据第一次全国水利普查公报［2］统计，中国中小型水库数目约占水库总数的99.2%，其库容约占总库容的19.6%。排沙系统的不完善，加之很多水库位于我国西北地区的多沙河流上，导致需要人工清淤的水库工作量大、任务艰巨。

中小型水库人工清淤常用几种方式有绞吸式挖泥船清淤、管道排沙等。绞吸式挖泥船利用绞刀等机械设备绞松疏浚区内淤积体，使得水、泥、石等混合形成泥浆，然后通过管道输送至指定区域。管道排沙依据其工作原理可分为气力泵式、自吸式等多种形式［3］。气力泵式或自吸式管道排沙的原理是利用压缩空气或上、下游水位差作为动力将库区原状淤积物吸入排泥管道输送至库外。

山区型水库库尾及变动回水区的淤积体内往往含有大量卵石等固体粗颗粒，上述几种人工清淤措施作业时经常会将大量粗颗粒（粒径约为0.5～150 mm）吸入管道。固体粗颗粒进入排沙管道后，不仅增大水流能量损失，而且因其运动速度明显小于管流流速，往往不能及时随浑水排出管外，易在逆坡、弯折管段处堆积，降低管道系统的输送效率。水库淤积物情况很复杂，管道排沙吸入粗颗粒不是小概率事件。管道内固体粗颗粒运动与流体运动产生互馈效应，体现在固体粗颗粒运移堆积行为会对流体结构如流场、流态等产生影响，进而导致流体对固体粗颗粒作用力发生改变，引起粗颗粒下一时刻运动状态的变化。管道流体粗颗粒运动过程是流体运动与固体粗颗粒运动双向反馈的过程。

这里重点介绍管流中粒径约为毫米甚至厘米级的粗颗粒输移问题。目前，国内外学者针对该问题采用理论分析、物理试验、数值模拟等手段开展了大量研究，取得了一系列代表性成果。下面主要对管道流体粗颗粒水力输送及互馈效应的基本理论、试验研究和数值模拟等方面进行总结，分析现有研究中存在的不足，并对将来的研究方向进行展望。

1 管道流体固体运动基本理论

管流中粗颗粒运动是典型的固液两相流运动问题。微观动理学方法是一种描述固液两相流运动特性的基本理论方法，其原理是将固体颗粒运动特性类比于气体分子动理论中分子运动。王光谦和倪晋仁等［4，5］以该理论为基础，提出在连续介质理论中，固相可用动力学理论描述，液相仍可用连续介质理论描述，并借助Boltzmann 方程和变分法得到了颗粒速度分布函数、颗粒浓度垂向分布理论公式。Ding 和Gidaspow［6］在微观动理学理论基础上引入颗粒重力、浮力和阻力项，构造了固相颗粒的守恒方程。随后，傅旭东等［7］在前人研究的基础上增加了升力继续研究，对固体颗粒在流场中的受力特性进行全面分析，建立了针对方型管低浓度固液两相流中固相颗粒运动数学模型。

有些学者假定固液两相可以相互渗透，可通过分别描述固相、液相的运动过程与相互间作用，进而得到两相流的运动特性。针对固相颗粒的处理方式的不同，该理论可分为双流体理论方法和离散颗粒理论方法。双流体理论方法对固相颗粒而言是一种积分的方法，将液相流体、固相颗粒均视为连续介质。Soo等［8］、刘大为等［9］、周力行等［10］、钟德钰等［11-13］在双流体理论领域开展了很多理论研究工作，认为固液两相占据相同的宏观空间，但又具有不同的运动性质，对固液两相引入压力、黏度的概念，建立的典型固液两相质量守恒方程和动量守恒方程如下：

式中：k=f，p 分别代表液相和固相；t为时间；g为重力加速度；εf、εp分别为液相、固相的体积分数且满足εf+εp=1；ρf、ρp分别为液相、固相的密度；Uf、Up分别为液相、固相的速度；τf、τp分别为液相、固相的应力张量；Kpf、Kfp分别为液相、固相交换系数。

离散颗粒理论方法对固相颗粒而言是一种微分方法，其将液相流体视为连续介质，固相颗粒视为不连续介质，通过计算颗粒实时受力特性及其对液相流体的反馈作用，获取其在流体中的运动轨迹。其中，液相流体控制方程为连续性方程和动量方程：

式中：μf为液相黏度；p为液相水体压力；Fpf为固相颗粒对液相水体的作用力，与固相颗粒运动方程中Ffp为一对相互作用力，属于两相间的耦合项。

选取固相颗粒中某一颗粒i，其控制方程为动量守恒和角动量守恒方程：

式中：mi、Ii、和ωi分别为固相颗粒i的质量、转动惯量、平动速度和角速度；为颗粒j作用于颗粒i的颗粒间接触力；为颗粒i所受到的重力；为液相流体作用于颗粒i的力；Mij为颗粒j作用于颗粒i的力矩。黄社华［14］和Liu［15］等进一步完善了离散颗粒理论方法中单颗粒运动方程的构建与求解。

理论研究建立了描述管道固液两相流运动的基本方程体系，考虑了管道近壁区对固液两相流的影响，能够从本质上很好地描述固液两相流运动的基本物理规律。然而，理论方程中的某些参数如τf、τp、Kpf、Kfp、Mij、、Mij等随固液两相流运动状态的演化特性尚不清楚，在分析过程中又引入很多假设，这使得仅采用理论方程无法得到固液两相流运动复杂规律。

2 管道流体粗颗粒水力输送试验研究

很多学者通过管道试验来测定流体、固体的宏观运动特征，用以探明理论方程中流体、固体关键参数与其运动状态之间的关系，进而可对理论进行佐证。目前管道试验大多采用清水或低含沙水流作为载流体，试验用到的粗颗粒粒径范围约在0.1～4.5 mm之间，管道流体的流速基本在0.8～3.5 m/s之间，通过开展管道流体粗颗粒试验研究取得了丰富的研究进展，根据粗颗粒在管道流体中运动形式可将试验研究分为粗颗粒推移运动特性和沉降运动特性两方面研究。

2.1 管道粗颗粒推移运动特性试验研究

国内学者曹斌和夏建新等［16-21］采用管道水力输送试验系统（如图1所示）开展了一系列天然石英砂粗颗粒在管道清水条件下运动试验研究，该试验系统能够观测粗颗粒的运动形式，获取管道输送时压差、粗颗粒输移量等。物理试验结果表明粗颗粒主要运动形式为滑动推移，少量存在跃动、滚动推移等方式，当粗颗粒粒径一定时，管道倾角越大，发生堵管的临界流速越低；当单位长度压差ΔP与水流平均流速V呈线性关系时，垂直管道堵管后粗颗粒无法再起动，当ΔP与V呈非线性关系时，粗颗粒可再次起动，并且建立了考虑流速、粒径、体积、管径等因素推移质运动形式无量纲参数表达式，提出了推移质管道输送时最佳输送速度和输送形式。

图1 管道水力输送试验系统示意图［16-21］Fig.1 Schematic diagram of pipeline hydraulic conveying test system

在上述管道水力输送试验系统基础上，吴优等［22］引入高速摄影技术和粒子成像测速系统（PIV），发现水平管道清水内推移质跟随性参数k在管道上部符合对数分布形式=ln(a1+b1k)，下部满足指数分布形式，其中D为管径，a1、a2、b1、b2分别为与粗颗粒粒径、平均流速、重力计算速度相关的参数。李时等［23］基于小浪底水库管道排沙原型试验，确定了管道输送最优阻力损失模型费俊祥模型，预测了高浓度输沙管道输送时最佳输送参数。

国外学者也进行了有关管道粗颗粒推移运动特性的试验研究并取得了一些进展。Vlasák 等［24］的试验结果表明部分推移质会在管道内会形成静止稳定堆积层；当管流速度较大时，推移质主要运动形式为跳跃型；水平管道沿程水头损失大于垂直管道；当管道倾角由0o增大至90o时，沿程水头损失先增大后减小，在管道倾角为30o时达到最大值。MatouŠek 等［25，26］在进行物理试验时也发现颗粒会在管道内呈现分层现象（堆积层和输运层），颗粒级配会对运动能耗产生影响。Alihosseini等［27］试验结果表明粗颗粒粒径比管壁粗糙度更能影响其临界速度，但颗粒整体速度受管壁粗糙度影响很大。

2.2 管道粗颗粒沉降运动特性试验研究

管道粗颗粒沉降运动主要应用于垂向管道提升深海矿石等粗颗粒等采矿工程领域。唐达生等［28-30］进行的垂直管道水力提升试验结果表明，群体颗粒均匀浮游速度随颗粒浓度、颗粒粒径的增大而增大，非均匀浮游速度随颗粒浓度的减小、颗粒密度的增大而增大；颗粒旋转速度随水流速度的增大、颗粒圆度的增大、颗粒粒径的减小、颗粒密度的减小而增大；输送速度和输送浓度会影响输送安全性，建议固体矿物提升速度应为矿物最大颗粒沉降速度的3倍，才能保证输送安全性。王锋等［31］详细归纳了当前典型垂直管道输送阻力计算公式，比较分析不同工况下各公式计算值和实测值，结果表明夏建新公式和Matousek 公式更适用于颗粒物料垂直管道水力输送阻力计算。Spelay 等［32］试验发现固相颗粒浓度对其沉积速度影响较小，颗粒沉积速度受管道倾角的影响较大，细沙则受其影响不大。夏建新等［33-35］研究了清水管流中粗颗粒浓度分布规律，构造了颗粒垂线最大浓度点相对位置高度与管径、颗粒粒径、平均流速、重力加速度的函数关系；研究了长条状颗粒在垂直上升流中最小输送速度的变化规律及特性，得到了长条状群体颗粒最小输送速度计算公式。

此外，Vlasák 等［36］分别采用了玻璃球、玄武岩卵石来模拟不同形状、密度的粗颗粒，以清水为管流载体，研究发现两种粗颗粒的管流水力要素几乎没有差异。阳宁等［37］探究了粗颗粒垂直管道水力输送系统的振动特性，研究表明颗粒浓度越大，则管道系统振动幅度越大，流体紊流涡激振动也随之加剧。

可以看出，不同学者在进行管道粗颗粒运移物理试验时，研究背景有所不同，采用的试验条件也各有差异，但是基本上均开展的是清水试验。目前已有的试验研究几乎没有涉及粗颗粒在高含沙水流中运动规律。高含沙水流浑浊不清，受限于物理试验观测技术，粗颗粒在高含沙水流中运动过程将难以捕获。水库清淤时高含沙水流和卵石等粗颗粒同时进入管道，因高含沙水流密度、黏性等物理特性与清水有很大区别，必将对粗颗粒运动产生一定的影响，以往清水条件下的研究成果直接应用到高浓度浑水流体时难免会带来误差。此外，水库清淤经常采用柔性管道，淤积物中含有大量的由泥沙细颗粒板结而成的黏性可破碎颗粒（板泥）。而蔡书鹏等［38］发现柔性管道边界在物理试验过程中会抑制流场整体能量，因此物理试验大多选用刚性管道边界条件，对柔性管道边界条件下管流粗颗粒运动研究很少，同时黏性可破碎粗颗粒输送规律的相关研究实不多见。

3 管道流体粗颗粒水力输送数值模拟研究

物理试验比较容易获取水沙运动现象及运动过程的宏观统计数据，而基于水沙运动基本理论的数值模拟技术能够直接获取泥沙运动过程中每个粗颗粒受力特征、颗粒运动轨迹及复杂水沙场的变化特征等相对微观数据，如基于Eulerian 描述方法的计算流体力学法CFD（Computational Fluid Dynamics）较易获取流体运动全过程中流场结构和流态演化特征；而基于Lagrangian 描述方法的离散单元法DEM（Discrete Element Method）则具有连续追踪固体颗粒运动轨迹的功能。

3.1 管道输送CFD数值模拟研究

CFD 兴起于20 世纪60 年代，在管道固液两相流模拟研究中取得了很多研究成果，其主要思想是将流体视为连续流体，将固相颗粒体视作连续拟流体，采用多相流的模式计算网格结点处流体、固体的运动与动力特征。

王继红等［39，40］采用双流体模型，分别进行了水平管道内水沙（固相粒径为0.09、0.27 mm）两相流、冰桨（固相粒径为0.1 mm）两相流运动过程的CFD 数值模拟。熊庭等［41］也利用此方法建立了水平管道清水和泥沙（粒径为0.09、0.27和0.44 mm）固液两相流的三维CFD 模型，研究了管道泥浆的流动特性，分析了管道输送速度、泥浆浓度、颗粒粒径等因素对其输送效率的影响规律。吴国英等［42，43］利用计算流体力学CFD 软件，对不同情况下管道内部流场进行了数值模拟，得到了管道内部压力场分布。陈建宏等［44］借助CFD 商业软件Fluent 模拟了充填料浆管道输运过程，得到了高浓度浆体流速与沿程阻力损失之间的函数关系。

国外学者也进行了大量管道固液两相流CFD 数值模拟研究：Kaushal 等［45］分别采用欧拉双流体模型和Mixture 模型分析了固相细颗粒（粒径为0.125 mm）在管道水流中的运动特性，对比了两个模型对于沿程水头损失、颗粒浓度分布模拟结果的精度。Messa 和Malavasi［46］通过调整CFD 中紊流弥散系数、两相摩擦系数和黏滞系数等模拟参数，较准确地预测了水平放置的90°弯管内固相颗粒分布特征。Sorgun和Ulker［47］计算了旋转状态下水平管道固液两相流（固相颗粒平均粒径为0.45 mm）的沿程水头损失。Singh 等［48］探究了高浓度固相颗粒条件下水头损失与流速、固相颗粒浓度之间的关系。

CFD 模拟的管流固相颗粒一般为毫米级以下的悬移质，此时将其视作拟流体是可行的；而粗颗粒的粒径一般较大、离散性强，颗粒对局部流场的反馈影响也较大，这与连续拟流体的假定有很大的差距。目前，管道粗颗粒CFD 模拟研究很少，部分研究是基于大量粗颗粒运动宏观统计规律进行的，无法根据颗粒的实际受力情况，跟踪模拟各个颗粒的运动过程，进而只能得到网格节点处均化特征，如图2所示。因此，仅采用CFD数值模拟方法来研究排沙管道流体粗颗粒水力输送及其互馈效应仍具有一定的局限性。

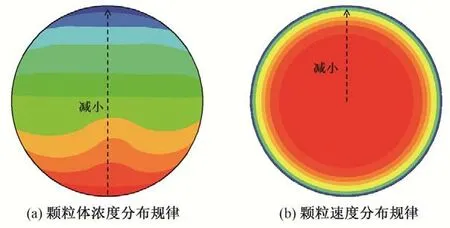
图2 CFD颗粒体积浓度分布Fig.2 CFD particle volume concentration distribution

3.2 固体粗颗粒DEM数值模拟研究

离散单元法DEM 是基于非连续介质力学理论的数值模拟方法，最早由Cundall［49，50］在1971 年提出，目前被广泛地应用于岩土地质工程、工农业制造等诸多领域。DEM 将研究对象离散概化成若干具有一定几何尺寸和物理参数的独立颗粒（单元），可连续追踪各个颗粒的受力、速度、位移等运动信息，主要应用于求解离散颗粒材料大变形、大位移等非线性问题。图3 给出了基于DEM 模拟得到的不同边界条件下颗粒剪切摩擦与碰撞等运动行为，可以看出DEM 能够精确描述颗粒的不同运动行为，这是CFD无法实现的。

图3 DEM模拟的不同边界条件下粗颗粒剪切摩擦与碰撞行为Fig.3 Particle shearing and collision behaviors of coarse particles under different boundary conditions simulated by DEM

输沙管道中卵石等粗颗粒属于典型的离散颗粒材料，目前很多学者采用DEM描述卵石、块石等粗颗粒的运动过程和动力特性［51］。来志强等［52-57］采用DEM 研究了岩体颗粒（粒径0.2～1.2 m）在不同边界条件下的剪切摩擦、碰撞等动力学行为、流动特性以及颗粒材料呈现出的尺寸分离现象。张翠兵等［58］采用DEM 模拟了块石颗粒（平均粒径为0.2 m）在振动荷载作用下受力运动过程，获得了每个块石的加速度、速度、位移随时间的演化规律。陈凯华等［59］模拟了抛石（粒径为0.2 m）在水中运动堆积过程，分析了抛石形状、质量等因素对其运动速度、堆积形态的影响规律。吴东旭等［60］借助DEM 模拟了砂卵石土（粒径为10～60 mm）直剪试验时剪切破坏现象，得到了颗粒剪切曲线。吴跃东等［61］进行了砂砾卵石土（粒径为2～60 mm）DEM 击实试验，探明了砂砾卵石土中卵石含量、粒径对其压实特性的影响。王俊等［62］利用DEM 模拟了土压盾构隧道掌子面失稳导致的卵石层（粒径为2～16 mm）变形运动过程，得到了卵石颗粒受力大小和位移变化。

DEM 在描述离散颗粒材料的运动特性方面具有天然优势。但是受限于其基本理论，DEM 仅能单方面考虑连续液相流体对离散固相颗粒的等效作用力，无法求解离散固相颗粒对连续液相流体运动的影响；当模拟的颗粒数目巨大时（百万级及以上），计算效率大幅降低，对于水流中毫米级以下悬移质的模拟并不适用。然而根据工程经验，当粗颗粒粒径与输沙管道管径尺寸相差1～2 个数量级时，粗颗粒运动将对局部流场乃至水流整体流态产生非常明显的影响。粗颗粒在管流中运移过程是流体与粗颗粒运动互馈的过程。因此，在采用DEM模拟粗颗粒运动的同时，还需结合CFD考虑粗颗粒对液相流体的影响。

3.3 流体-固体耦合CFD-DEM 数值模拟研究

流体-固体耦合CFD-DEM 数值模拟方法是将CFD 和DEM两种数值模拟方法耦合，充分发挥CFD、DEM 两者的模拟特点与优势。图4 为CFD-DEM 耦合求解过程示意图，CFD 求解连续液相后，得到流场信息，计算得到连续液相对离散固相的作用力，如浮力、拖曳力等，并将计算结果传递给DEM；由DEM 计算离散固相的受力情况，根据其运动方程计算得到离散固相新的位置、速度等信息，以及对流场的反作用力，计算结果传回CFD，由CFD 更新流场信息并产生对离散固相新的作用力，整个过程就这样循环往复实现耦合。可以看出两者主要通过液相、固相控制方程中相互作用力项Fpf和来进行动量和能量的交换。

图4 CFD-DEM 耦合求解原理示意图Fig.4 Schematic diagram of CFD-DEM coupling solution principle

目前，国内外学者采用该方法已开展了初步的管道流体固体粗颗粒运动研究工作，利用CFD 计算流体的运动过程，得到流场分布特征［图5（a）所示］；利用DEM 计算毫米级甚至厘米级固体粗颗粒的运动速度和位置［图5（b）所示］，并进行实时数据交换。

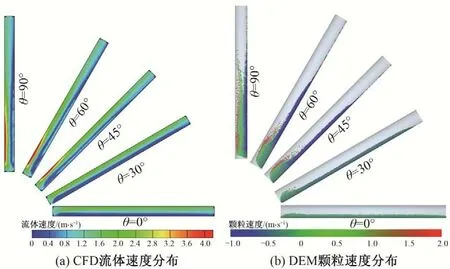
图5 CFD-DEM 模拟得到管道颗粒和流体速度分布示意图Fig.5 CFD-DEM simulation is used to obtain the velocity distribution of pipe particles and fluid

在复杂管道水沙运动机理方面，李亚林等［63］采用CFDDEM 模拟了固相颗粒在水泵变曲率弯管内的运动过程，开展了流场网格、湍流模型、颗粒接触模型等敏感性因素分析，得到了颗粒属性、管道几何特征和流体雷诺数对颗粒运动特性的影响规律。喻黎明等［64-67］和唐兆家等［68］采用该方法分别模拟了灌水器［64，65］、水力旋流器［66，68］、网式过滤器［67］中复杂流道内水沙运动过程，分析了流道内水流流场分布特性、单个固相沙粒运动轨迹、速度演化和沙粒群体运动堆积特性，得到了管内回流区、涡旋区和滞流区变化与沙粒分布之间的内在联系，从沙粒个体运动、群体运动等微观角度明确了水沙运动机理和分离机制。关英杰等［69］数值研究表明垂直管道输送速度随着颗粒粒径增大而减小，颗粒群输送颗粒存在一定程度的碰撞，对输送能量的损耗很大。

Akhshik 等［70-75］利用CFD-DEM 开展了钻井过程中流体与岩屑在移动管道内运移机理研究，模拟了简单规则非圆球碎石颗粒与流体在钻井管道内输运过程，探究了管道转速［70］、碎石颗粒形状［71］、抗转动系数［72］和接触摩擦系数［73］对碎石粗颗粒运动速度、堆积形态、分布位置和管道堵塞程度的影响机制；此外，Akhshik 等［74］通过改变钻杆管道的旋转速度、机械钻速、倾斜角度和管道流速等因素，得到了不同工况下固液两相流动力特性演化规律；在此基础上，进一步考虑管道液体流量、注气量、注气压力和环境温度等因素，深入研究了管道气固液三相流运动特性［75］。Xiong 等［76，77］提出了3 种水平管道粗颗粒输运机制即定床流、滑床流和滑动流，并从颗粒受力角度解释了其形成机制，认为滑动流输送效率最高。

CFD-DEM 具有模拟固液两相流中粗颗粒碰撞行为的功能，还被应用于大粒径固相颗粒对管道内壁冲蚀破坏的研究中。姚利明等［78，79］利用该方法分析了缩径管道内沙粒碰撞行为和缩径斜面受力分布，得到了沙比、流体黏度对管道内部冲蚀深度的影响规律。Varga 等［80］研究了圆弧型刚性管道、柔性管道破损程度、破损模式与水流中固相颗粒冲击内管壁角度、能量之间的关系。Cheng等［81］模拟了不可压缩幂律流体与固体颗粒在缩径管道中运动过程，总结了缩径管道破坏速率、破坏面积随流体速度、黏度和颗粒碰撞频次的演化趋势。Chen等［82］探讨了弯头角度对颗粒运动特性、流场分布特征、颗粒冲击管壁速度与角度分布特征的影响机制。Tao等［83］通过模拟计算揭示了固相颗粒接触力、液压力、配位数和密实度等参数演化过程与管壁破坏过程的内联机制，定量分析了颗粒密度、孔隙率、粗糙度和级配分布对管道流动的影响规律。

在管道固液物料输送特性CFD-DEM 数值模拟研究方面，Huang等［84］模拟了不同法兰连接工况下排泥管道固液两相流运动过程，得到了不同工况下流场、颗粒运动轨迹和颗粒体积率等变化规律。Dabic 等［85］在模拟中引入了声波场的概念，考虑了固相颗粒和流场受到的声波震动作用力，阐明了声波场对固液两相流运动特性的影响机制。Yang 等［86］研究了浆体和块石在管道中运动特性，分析了管道泥浆流速、块石体积分数和管道倾斜角度对泥浆速度场分布、压力分布、水头损失的影响规律。Akbarzadeh 等［87］对矩形管道内黏性固体在牛顿流体中的运移过程进行了模拟，考虑了颗粒碰撞力、胶结力和水动力，探讨了浮力、黏聚力和拖曳力对颗粒运动机制和团聚模式的影响机理。Guo等［88］模拟了水平管道内预置沙粒堆积体在水流带动下的运动过程，分析了流场应力张量项三种简化求解方式对数值模拟结果的影响规律。Zhou［89］模拟了垂直管道中水力输送粗颗粒的过程，研究了传送颗粒浓度、传送速度和颗粒粒径对管道输送的影响规律。Januário 等［90］计算得到了管流粗颗粒临界沉积速度，小于此速度时颗粒在管道底部堆积形成静止颗粒层，大于此速度则颗粒不再堆积。

流体-固体耦合CFD-DEM 数值模拟目前已成为国内外研究热点，近年来学者们已将其成功地应用于管道固液两相流水力输送研究中，特别是对管流中毫米级甚至厘米级固相颗粒运动特性的研究。许多成果颇具特色，均具有一定的学术价值与参考意义。然而，目前数值模拟研究中仍存在一些不足与空白：①绝大部分CFD-DEM 数值模拟采用圆形颗粒或者规则形状颗粒，无法反映复杂的颗粒形状，这与实际粗颗粒不规则形状相出入。②CFD-DEM 数值模拟参数应通过物理试验或现场试验直接率定，使得CFD-DEM 数值模拟结果能够直接应用于工程实践，而部分CFD-DEM 数值模拟参数取值没有依据，就会导致数值模拟结果脱离实际应用。③水库清淤时柔性与刚性管道互联使用，淤积物中含有大量由泥沙细颗粒板结而成的黏性可破碎粗颗粒；然而目前模拟的管道多为刚性管道以及无黏性颗粒，对柔性管道和黏性颗粒输运的模拟很少见。④有必要将细观层面固体颗粒的能量演化规律与流体的能量演化规律相结合以揭示管道输送能耗机制。⑤大部分数值模拟所采用的RANS 湍流模型能够反映出流体运动基本规律，但对涡旋的模拟精度不高。未来可考虑在管流中采用对涡旋模拟精度较高的大涡模拟LES 湍流模型［91-93］，以提高对管流涡旋发展机制的认识。

4 总结与展望

（1）目前理论研究很好地建立了流体固体运动控制方程体系。但方程中一些关键参数随固液两相运动状态的演化特性还不十分明确，还需通过物理试验与数值模拟进一步补充研究。

（2）受限于测试技术，目前相关试验研究大多采用清水或低含沙水流作为管道载流，而高含沙水流物理特性与清水有很大区别，以往清水条件下的研究成果直接应用到高浓度浑水流体时难免会带来较大误差。

（3）CFD-DEM 数值研究大多采用简化的圆形或规则形状的颗粒，对颗粒复杂形状的模拟不足。CFD-DEM 数值模拟参数应通过物理试验或现场试验得到，使得数值模拟结果能够满足工程应用要求。

（4）目前物理试验和数值模拟大多采用刚性管道边界和无黏性不可破碎的粗颗粒。柔性管道边界以及由泥沙细颗粒板结而成的黏性可破碎粗颗粒输送规律研究十分不足。

（5）基于CFD-DEM 数值模拟技术，可从细观层面上将固体颗粒的能量演化规律与流体能量演化规律相结合以揭示管道系统能耗机制以及宏观尺度上输移规律，这方面还需要进一步研究。

（6）大多数值模拟采用的RANS 湍流模型对涡旋的模拟精度不高，有必要进一步采用精度更高的大涡模拟LES 湍流模型，以提高对管流涡旋发展机制的认识。