基于MOOSE框架的热力全耦合仿真方法研究*
陈智源,周晓明,方 芳,何 敏,刘 浩,3,孙佳宁
(1. 电子科技大学机械与电气工程学院,四川成都 611731;2. 中国电子科技集团公司第十研究所,四川成都 610036;3. 中国电子科技集团公司第二十九研究所,四川成都 610036;4. 电子科技大学广西智能制造产业技术研究院,广西柳州 545003)
引 言
热力耦合是指结构中温度场的变化对结构的影响以及结构变形在外部载荷作用下对温度场的影响,即结构、温度场通过交互作用而相互影响的物理现象。热力耦合问题广泛存在于航空航天[1-3]、机械[4-6]、半导体微电子[7-9]等领域,特别是随着现代电子设备向着高度集成化的方向发展,电子设备内部的热力耦合效应更为明显,对电子设备进行热力耦合效应研究的需求逐渐增加。
通过仿真工具对多物理场耦合现象进行工程计算,是现代电子设备研究与设计中常用的方法[10]。目前能够进行热力耦合仿真的多物理场耦合工具有Ansys Multiphysics,COMSOL Multiphysics,ABAQUS,ADINA,MATLAB等。ANSYS提供结构力学、热学等计算程序,程序之间有给定接口,主要耦合方式为顺序耦合、算子分裂和固定点迭代,但核心代码封装,改动耦合方式和求解算法的难度较大;与ANSYS不同,COMSOL Multiphysics是在同一框架内的多场耦合,支持多种模块,部分计算能够实现牛顿迭代的全耦合,主要耦合方式是顺序耦合和固定点迭代;ABAQUS和ADINA可以全耦合求解热电耦合;MATLAB是基于代码的数学软件,通过特定代码可以实现各种耦合算法。
上述基于牛顿迭代的耦合计算工具在面对多场同时求解时可能产生大型稀疏矩阵难以收敛求解的问题,而其他基于多求解器并采用顺序耦合、固定点迭代等的传统耦合策略的仿真软件在双向耦合模式下进行多场强耦合仿真时经常难以收敛,而且多个求解器之间存在异构网格映射、数据传递的问题。鉴于上述问题,亟需探索一种适用于电子设备热力强耦合仿真的新方法。多物理场耦合仿真(Multiphysics Object-Oriented Simulation Environment,MOOSE)[11]作为新一代开源多物理场仿真框架,采用Jacobian-Free Newton-Krylov (JFNK) 方法[12]求解强耦合问题偏微分(Partial Differential Equation, PDE)方程组。本文开展基于MOOSE框架的热力全耦合计算方法研究,有望实现高性能热力耦合仿真,具有广阔的应用前景。
1 方法
1.1 基于MOOSE框架的耦合仿真应用程序开发
实现热力耦合首先需要在MOOSE框架的基础上开发求解程序。如图1所示,MOOSE框架分为3层。底层由libMesh有限元库、PETSc等组件构成。libMesh主要进行网格读入、有限元离散、残差矩阵形成和结果输出;PETSc求解器则可以求解残差矩阵。中间层为框架通用接口,包括耦合接口、残差估算和雅可比矩阵估算。物理层包括内核系统、边界条件和材料系统。工程师可在这3层基础上结合需求开发应用程序。

图1 MOOSE框架结构示意图
MOOSE热力耦合仿真应用程序的核心是内核(Kernel),目前,MOOSE框架中内置了热学、化学、N-S方程、接触、弹性力学、时间处理等多种内核。MOOSE框架下的多场耦合基于多个单场模块的内核组合实现,因此为实现热力耦合,需要构建结构力学和传热学模块。
结构力学模块基于弹性力学方程构建。典型弹性力学问题的基本方程如下:
平衡方程为

式中:σ为应力;F为体积力,即F= [Fx Fy Fz]T;A为微分算子。A的矩阵形式为
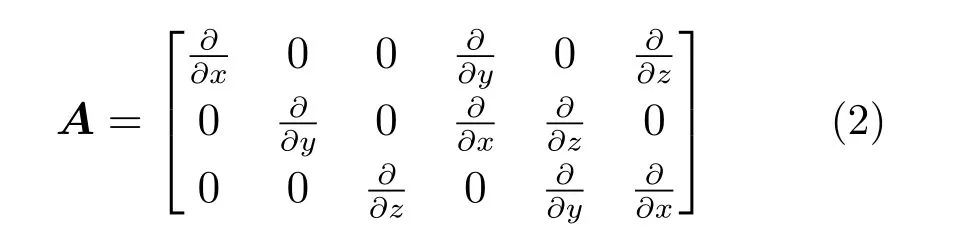
几何方程为

式中:ε为应变;u为位移。对于小应变的线性弹性问题,采用线性化小应变理论,有
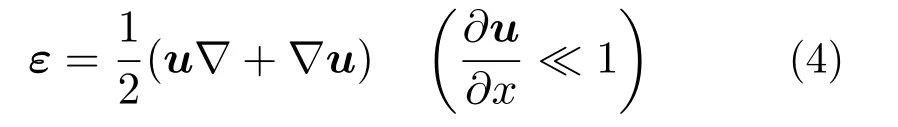
式中,∇为那勃勒算子。
应力应变本构方程为

式中,D为弹性矩阵,它完全取决于材料的弹性模量E和泊松比ν。
将几何方程代入本构方程,再代入平衡方程得:
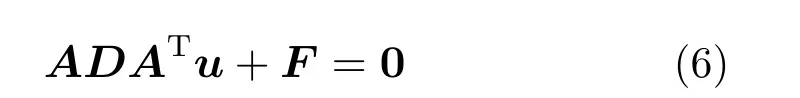
传热学模块构建基于热传导功能,有瞬态热传导方程如下:

式中:cp为比热容;ρ为密度;T为温度;t为时间;k为导热系数;x为空间坐标系下的矢量;˙q为热源。
瞬态热方程弱形式为:

式中:φi为有限元试函数;Th为有限元结果;ˆn为边界向外的法向量。
将上述理论模型写成代码,构成了热传导内核。热力耦合中使用的是ADHeatCondution类内核,此类内核是热传导中热扩散方程在自动微分框架下的实现,为前向微分。ADHeatConduction内核实现了傅里叶定律给出的热方程,其中热通量q为:

在MOOSE中,在默认情况下,热内核在位移网格上运行,其变形由力学模型计算。其本质是通过将热传导计算嵌入到网格可运动的力学计算过程中来求解热力问题,热和力的耦合通过热膨胀本征应变模块施加。对于力学模块的本征应变,需要将力学模块的应力-应变方程替换为下面的热弹性体的应力-应变方程:

式中:ε0为温度引起的应变;α为热膨胀系数;T0为参考温度,即低于该温度材料收缩,高于该温度材料膨胀。
1.2 应用程序校核
热力强耦合现象中温度场产生热变形,热变形又会影响传热,温度场、变形场因此而耦合。本文选择商业软件COMSOL Multiphysics中简单的基准案例(即钢材热变形模型[13-14])在所开发的应用程序中进行计算,所得结果与COMSOL Multiphysics结果进行对比,完成程序的校核。
该模型为一长宽高均为100 mm的钢块,其比热容为453 J/(kg·K),导热系数为45 W/(m·K),杨氏模量为2.1×1010Pa,泊松比为0.3,密度为7 850 kg/m3。在Trelis Pro 16.5中对模型分网,采用尺寸为2 mm的正六面体网格,模型及网格如图2所示。
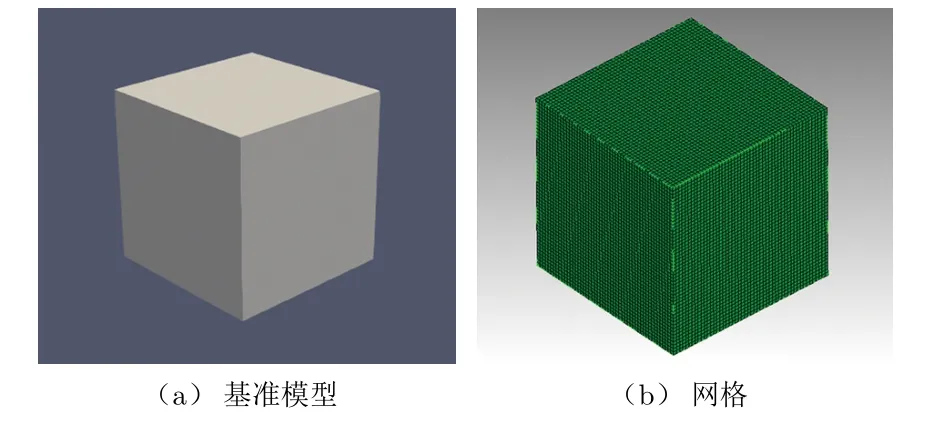
图2 用于校核的基准模型及其网格
在MOOSE中按如下步骤编写输入文件:
1)在输入文档中写入网格命令,并将网格命令导入外网格。
2)主变量规定为钢块温度和三维形变量disp_x,disp_y,disp_z,且均为一阶拉格朗日插值函数。
3)同时写入弹性力学和热传导两内核。
4)设置边界条件。固体外表面设置为狄利克雷边界,在固体一角施加三向固定约束,使材料可以各向形变。
5)设置材料。设置钢材料的杨氏模量、泊松比、导热系数和热膨胀系数。参考温度设为293.15 K。
6)设置求解器。求解算法为Preconditioning Jacobian-Free Newton-Krylov(PJFNK)方法,非线性相对容差为1e-14,线性相对容差为1e-6,默认预处理。
1.3 电子设备热力耦合仿真
电子设备往往由于其中的高功率组件发热而变形,这种问题涉及到热力强耦合。为探索将开发的应用程序应用在复杂电子设备中的可能性,本文面向某机载相控阵天线阵面进行热力耦合仿真。
采用的天线对象来自文献[15]设计的相控阵天线阵面。该天线的总体尺寸为316.8 mm×24 mm×0.404 mm,贴片及微带线为铜质材料,介质板材料为Rogers RT/5880。其T/R组件尺寸为60.6 mm×56.4 mm,T/R 组件单通道总功率为45.88 W。天线高功率放大器的功率为44.80 W,极限热功率为60.65 W,尺寸为6.77 mm×77 mm×2 mm,材料为GaAs。电源尺寸为100 mm×80.74 mm×8 mm,外壳为铝合金。使用Trelies Pro 16.5工具对模型分网,采用正六面体网格,单元尺寸为2 mm,生成如图3所示的网格。

图3 某相控阵天线冷板及阵面模型
2 结果与分析
2.1 校核仿真结果与分析
设置不同热边界条件,在MOOSE框架下运行编制的应用程序,所得热力耦合位移结果如图4所示。
在COMSOL Multiphysics中调取上述基准案例结果,对比MOOSE应用程序仿真结果与COMSOL Multiphysics结果,见表1。

图4 热力耦合仿真校核案例仿真结果
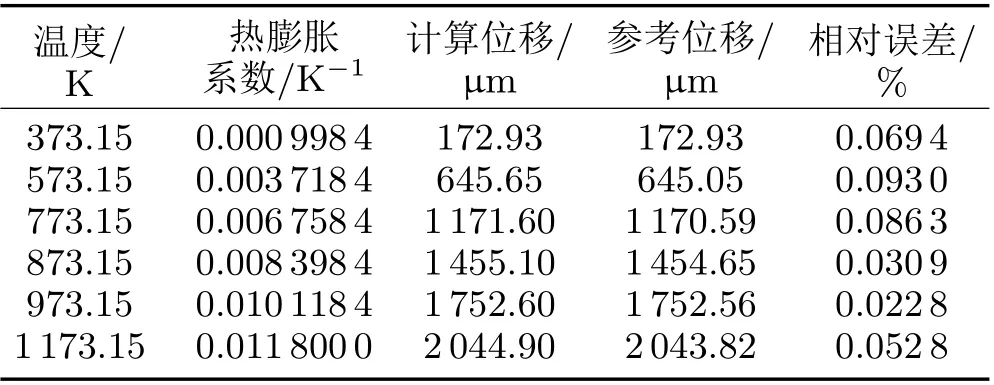
表1 热力耦合校核案例仿真结果
结果表明,MOOSE框架下的位移极值与商业软件COMSOL Multiphysics基准案例提供的位移数值的最大相对误差小于0.1%,说明热力耦合内核能够进行正确、准确的计算。
2.2 天线仿真结果与分析
在MOOSE框架下运行所编制的应用程序,所得热力耦合结果如图5和图6所示。
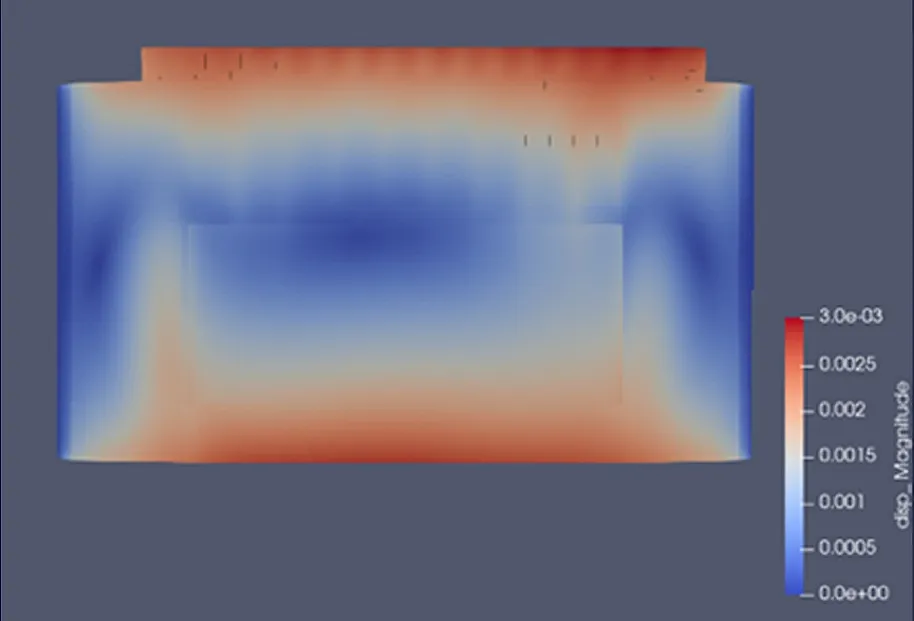
图5 天线热力耦合仿真位移云图

图6 天线热力耦合仿真温度云图
采集热源中心点的温度和热应变数据,结果见表2。由表2可知,天线阵面中心位置温度高,靠近边缘位置温度低,同时天线面板上下两侧的热变形较明显,所得结果与工程经验相符。

表2 热力耦合结果温度及热位移表
3 结束语
本文面向电子设备热力强耦合仿真需求,基于MOOSE框架内置的结构力学和传热学内核,编写了全耦合仿真程序,并且通过商业软件的基准案例对仿真程序进行了校核,进而将仿真程序应用于工程案例。通过对某相控阵天线进行热力耦合仿真,得到了天线阵面温度场和位移场的数据。本文的主要结论如下:
1)在校验案例仿真中,基于MOOSE框架的热力耦合仿真应用程序能够实现热力全耦合仿真。通过在弹性力学内核框架中嵌入传热学的热应变方程组,可以实现网格共享。仿真所得温度场下的热变形位移结果与基准案例结果基本一致,表明所开发的程序可正确计算热力强耦合问题。
2)相控阵天线阵面热变形仿真结果表明,由于天线介质板与冷板表面绑定接触,热变形量为0,因此脱离冷板约束后,天线热变形量呈增加趋势,最大变形量出现在中部上边缘。所述结果符合预期,反映基于MOOSE框架的热力强耦合仿真可应用于复杂电子设备,有望解决当前电子设备热力强耦合的迫切需求,具有广阔的应用前景。

