一道课本习题与高考题引发的变式探究
文/陆丰市玉燕中学 程广安
人教A版高中数学新教材习题是在原先人教版旧教材习题的基础上进行了完善,适合不同层次的学生,教材习题具有典型性、代表性、渗透性、延续性的特点,它能帮助师生更好掌握课本知识。研究教材习题是教师备课教学中不可缺少的一个重要部分。
一、问题引出
教材原题(人教A版高中数学新教材第二册第54页22题)已知a,b,c分别为△ABC三个内角A,B,C的对边,且b-c=0,(1)求A;(2)若a=2,则△ABC的面积为求b,c。
题目评析:第(1)题求角A,条件中只给了一个等式,那么我们就要把这个等式化简,通常有两种方法,一是全部化成边,二是全部化成角,而这道题很明显,采用化角的方法,把等式中的边全部通过正弦定理化成角的正弦的形式,化简求出结果;第(2)题通过面积公式及余弦定理可以求出b+c的和,又由bc的积可以求出b,c的值。
这道题第(1)小题有点难度,如果没把B转化成用A+C表示,那么这道题后面就无法化简求值,但是我们为了应对高考,不能就题论题,而应该对题目加与研究,特别是要将题目进行变式思考、变式探究,以实现对知识的透彻理解。
问题的变式1:如果把这道题第(2)题条件换成,若a=2,求△ABC的面积的取值范围,那该如何求解。
问题的变式2:如果把这道题第(2)题条件换成,若a=2,求△ABC周长的取值范围,那该如何求解。
通过不断更换条件,实现对正余弦定理充分理解,以便把教材内容吃透。带着这些问题,我们研究如何做到对题目进行变式思考。
二、考题链接
(2020年浙江卷18题)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且求B角;(2)求cosA+cosB+cosC的取值范围。
这道题从题目结构看没什么特殊之处,但是从研究高考方向考虑,我们必须对题目进一步深入探究,以更好地让学生掌握知识的规律与方法。
三、变式探究
从教材习题与高考习题引发思考,如何对题目进行变式探究呢?对解三角形这部分知识,可以从以下方面进行深入思考。
1.从三角函数的名称角度进行变式
思考1:既然高考题可以考查两个角余弦的和的取值范围,那是否也会考查两个角正弦的和的取值范围呢?
题目1:在锐角△ABC中,已知角,求sinA+sinC的取值范围。
解:sinA+sinC=sin(B+C)+sinC
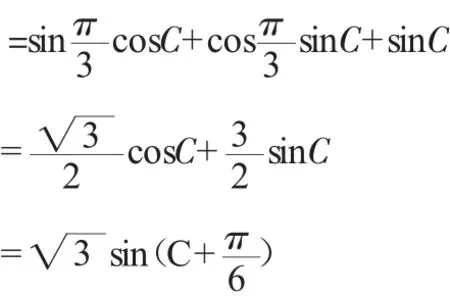
评析:从三角函数名称上进行变式,进一步探究问题本质。
2.从三角函数的运算角度进行变式(差,积,商)
思考2:既然可以考查两个角正弦的和的取值范围,那是否也可以考查它们的差、积、商的取值范围呢?
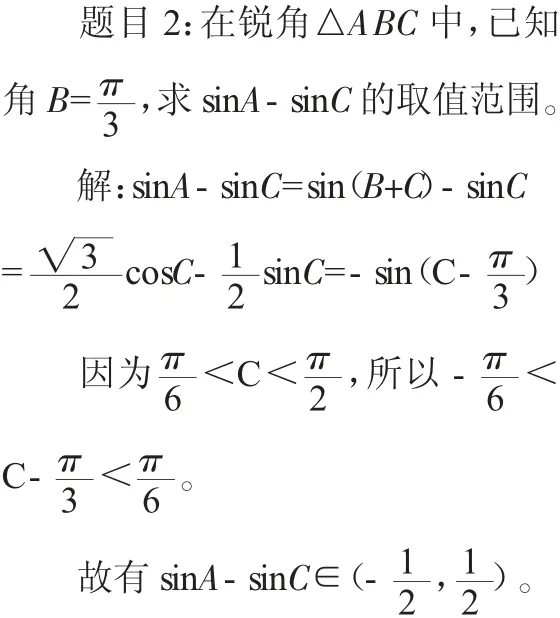
评析:从上面两个角的正弦之和做变式求两个角的正弦之差的取值范围,方法上还是一样,把双变量转化到单变量上来。
总结:通过把双变量转化为单变量,再利用角域进行求解范围。
3.从三角形中边的角度进行变式
思考3:从边的角度进行变式,实际上就回到上述教材习题的变式上,如果探究边的范围,又该如何解决?
题目3:在△ABC中,已知角求a+c的取值范围。
解:由于求的是两个变量的和的取值范围,可以考虑利用基本不等式求解,因为,所以ac=a2+c2-9,故有(a+c)2-9≤从而可以得到a+c≤6,又因为a+c>3;故a+c∈(3,6]。
评析:求两边之和的取值范围,可以将边的取值范围转化到角的取值范围,另外也可以从基本不等式与三角形的性质角度入手,得到两边之和的取值范围。
思考4:上面变式是求两边之和范围,那三角形的边是否也可以通过减法,乘除求取值范围呢?
题目4:在△ABC中,已知角求a-c的取值范围。题目5:在△ABC中,已知角的取值范围。
题目6:在△ABC中,已知角的取值范围。
题目4至题目6显然都可以化成对应角的正弦求解,转化成前面熟悉的问题,对于题目6还可以用基本不等式求解。
4.从三角形边的几何意义进行变式
思考5:从教材习题变式1、变式2我们可以考虑三角形的边角之间关系,由正弦定理我们知道若三角形的一角与一角的对边为已知时,我们可以得到此三角形的外接圆,由三角形的外接圆特殊的几何意义可以快速地解决三角形周长或者面积的取值范围。
题目7:在△ABC中,已知角求△ABC周长的取值范围。
题目8:在△ABC中,已知角求△ABC面积的取值范围。
在平时的教学中,教师应该充分利用教材习题与历年高考题,通过对教材习题的变式探究,培养学生思维发散能力,最后促进数学核心素养的提升。

