问答题“一题变式”分层作业设计初探

文/广州市南武实验学校 陈倩婷

有效分层作业既要满足学困生提高学习积极性，中优等生有拓展的方向，也要满足教师批改方便等优点。笔者以一道常见的“手拉手”全等三角形中等题为例，设计“一题变式”分层作业，通过各层次激励晋级手法展开初探。

一、母题呈现

如图1，C为线段AB上一点，△ACM，△CBN是等边三角形．AN，BM，相交于点O，AN，CM，交于点P，BM，CN，交于点Q，问题（1）求证：AN=BM；问题（2）求∠AOB的度数；问题（3）连接PQ，求证：PQ∥AB。

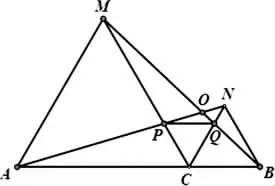
图1

二、设计前准备工作

1.挖掘母题的考点

这是道双等边三角形为背景，“手拉手”全等三角形模型（边角边）典型题目，涉及凑成三角形内角和模型，二次全等判定，等边三角形判定，直线平行判定等知识，题目条件简明，考点明显，满足现阶段学生应掌握的基本图形和拓展需要。

问题（1）为常规全等三角形判定题目，符合“手拉手”的边角边判定考点。问题（2）由问题（1）全等三角形的对应角相等性质推出结论。问题（3）综合考查学生提高看图分析能力，整理条件和结论能力。

2.抽取学生完成母题，找出设计方向

没有老师引导下，学生有的在规定时间15分钟内完整完成，有的只完成部分，有的超出规定时长。

由此可见，直接搬原题是没有达到课后作业评价作用，对学困生太难，中等生不能规范完整完成，尖子生没有拓展方向。

解决此问题，可以通过原题条件下设计“脚手架”问题，可以让学困生有抓手，中等生有提示，优等生有拓展方向，让各层次学生得到发展。

三、“一题变式”分层作业设计、

生可以在三道题中自由选择一题目完成，考点和母题是一样，只是为各层次学生建立“脚手架”和思维拓展，降低教师批改作业压力。具体三题变式如下。

题目1：如图2，C为线段AB上一点，△ACM，△CBN是等边三角形．AN，BM，相交于点O，AN，CM，交于点P，BM，CN，交于点Q，问题（1）写出等边△ACM，△CBN相等的线段，相等的角；问题（2）证明：△ACN≌△MCB；问题（3）写出除等边三角形外，相等的线段有哪些？哪个角也为60°？

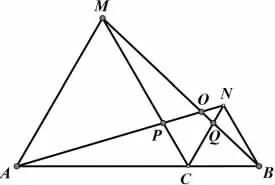
图2

题目2：如图3，C为线段AB上一点，△ACM，△CBN是等边三角形．AN，BM，相交于点O，AN，CM，交于点P，BM，CN，交于点Q，（1）求证：AN=BM；（2）写出除等边三角形的内角，等于60°的角还有哪个？请证明；（3）找出隐藏的全等三角形，试证明；（4）连接PQ，直接判断△CPQ为什么特殊三角形。

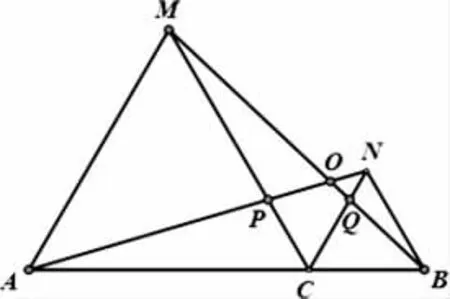
图3

题目3：如图4，C为线段AB上一点，△ACM，△CBN是等边三角形．AN，BM，相交于点O，AN，CM，交于点P，BM，CN，交于点Q，（1）求证：AN=BM；（2）求∠AOB的度数；（3）连接PQ，求证：PQ∥AB；（4）看图5，当A、C、B不在一条直线上，（1）（2）结论还成立吗？（5）看图6，若等边三角形改成等腰直角三角形，(1)结论成立吗，∠AOB是定值吗？

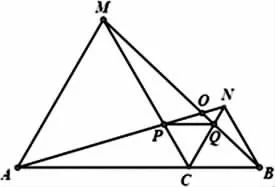
图4

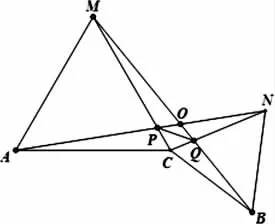
图5

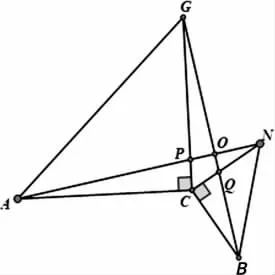
图6