结合工程关联实例的自动控制原理二阶系统教学内容探索

马 彦， 唐志国， 胡云峰， 李佳怡，2

（1.吉林大学a.通信工程学院；b.汽车仿真与控制国家重点实验室，长春 130022；2.吉林化工学院信息与控制工程学院，吉林 吉林 132022）

0 引言

自动控制原理是自动控制技术的理论基础，内容丰富、涉及知识面广，在整个专业课程体系中占据着非常重要的地位［1-5］。在控制工程中，不仅二阶系统的典型应用极为普遍，而且很多高阶系统的特性在一定的约束条件下可以用二阶系统的特性来表征并分析［6-10］。因此，研究二阶系统的建模和分析方法具有较大的实际意义。

1 系统建模思想分析

控制系统按照其内部规律及其结构参数是否完全已知，可以分成白箱、灰箱与黑箱系统。在建模方法中，分析计算法（又称机理法）和实验法（又称系统辨识）可以都可以很好地处理白箱与黑箱的问题。而现实工程中经常遇到灰箱问题，即：只知道系统部分变化规律，另一部分规律则需要实验测得，所以常常是两种方法综合使用。

控制系统的建模只是一种手段，目的是为了分析和设计系统的性能，在建模过程中想要获得更为简化的数学模型，采用抓住主要矛盾，忽略次要因素的方法，如有些情况下摩擦力可忽略不计、直流电机电枢电路中电阻较小亦可忽略等，其控制系统分析过程如图1所示。但是，这些忽略的物理量通常会对系统造成一定的影响，甚至会影响数学模型的精准度，因而，在具体工程系统中需要具体问题具体分析，综合考量。

图1 控制系统分析过程

2 工程案例建模与分析

二阶系统在自然界和工程领域广泛存在，其时域分析是自动控制原理课程的一个重点和难点［11-13］，在本专业实践中占有重要地位，控制类课程群实验设置如表1所示，并且其分析方法又对计算机控制系统、电力拖动及过程控制等课程有借鉴意义［14-15］。

表1 控制类课程群实验设置

2.1 车辆减震器

车辆减震器系统实际上是一个振动阻尼器，可以抽象成质量-弹簧-阻尼器物理模型，如图2所示。

图2 车辆减震器实例分析

图2（b）中，以外力F（t）作为系统输入，滑块m的位移x（t）作为系统输出，根据力学中的牛顿第二定律，以及弹簧的虎克定律、阻尼器的粘性摩擦定律，整理得：

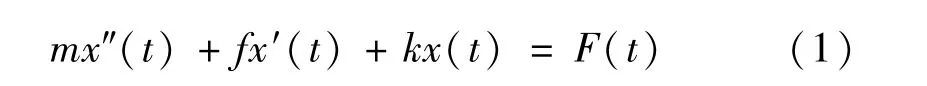
2.2 振荡器

振荡器是一种能量转换装置——将直流电能转换为具有一定频率的交流电能，其构成的电路叫振荡电路。振荡器可抽象为RLC无源网络，如图3所示。

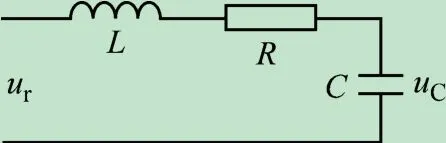
图3 RLC无源网络

以输入电压ur（t）作为系统输入，电容上分得的电压uC（t）作为系统输出，利用电学中的基尔霍夫电压定律以及RLC的伏安特性关系，有：

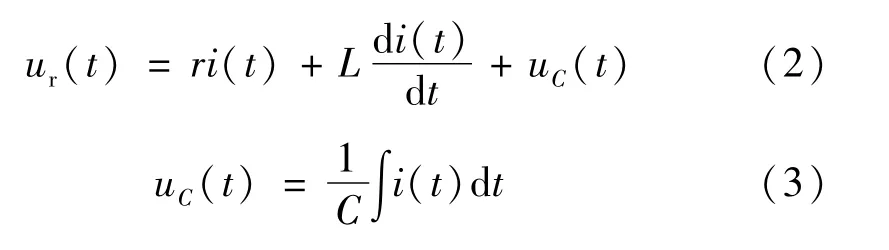
消去中间变量并整理，RLC无源网络的微分方程模型为：

2.3 直流电动机

在直流电动机中，以电枢电压ua（t）作为系统输入，电动机转速ωm（t）作为系统输出，因此，电枢控制直流电动机的微分方程模型为：

式中：La和Ra分别为电枢电路的电感值与电阻值；Jm和fm分别为电动机和负载折合到电动机轴上的转动惯量和黏性摩擦因数；Cm为电动机转矩系数；Mc（t）为折合到电动机轴上的总负载转矩。

2.4 双容系统

双容水槽是工业生产过程中的常见控制对象，它是由两个具有自平衡能力的单容水槽上下串联而成。液位的高低在生产中是一个重要的参数，生产中常需测量容器内的液面高度以计算产品产量和原料消耗，作为经济核算的依据。化工生产等过程控制中的双容水箱系统如图4所示。以流入第1个水箱的流量为系统输入，第2个水箱的液位高度为系统输出。因此，双容水槽一般表现出二阶特性，利用动态平衡关系，有：

图4 双容水箱系统

式中，C1和C2分别为第1、第2个单容水箱的过程容量系数。

2.5 双连杆刚性机械臂

针对工业过程中应用广泛的双连杆刚性机械臂，以关节电动机输出转矩为系统输入，机械臂第2根连杆的关节运动转角为系统输出，利用机械臂系统力学及运动特性，有：

综上分析，车辆减震器、振荡器及直流电动机3个系统的传递函数皆可统一写成欠阻尼的二阶形式：

此外，双容系统和双连杆刚性机械臂均可视为双惯性环节的传递函数，亦可被统一写成过阻尼的二阶形式：

3 高阶系统模型简化方法

在控制领域存在大量的高阶系统，有时也会因系统反应时间过长而出现纯滞后特性，这些都无形中增加了系统分析的难度，因此，需要对模型进行简化处理。

3.1 寻求主导极点

在工程实践中，通常希望被控系统不仅具有较快的响应速度及有一定的阻尼程度，还要求减少死区、间隙和库伦摩擦等非线性因素对系统性能的影响。因此，在分析高阶系统性能时，选取在系统的时间响应过程中起主导作用且随时间衰减缓慢，距虚轴最近的闭环极点作为主导极点，忽略对响应过程影响甚微的非主导极点进行近似分析。

当惯性时间常数T3与T4接近，且T2＜5T1时，高阶系统

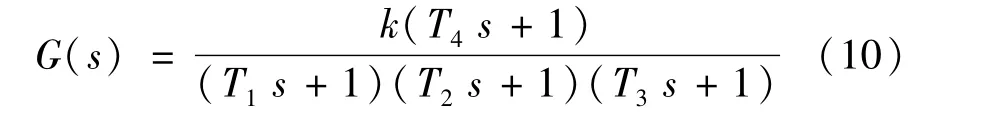
可以近似为一阶系统，即

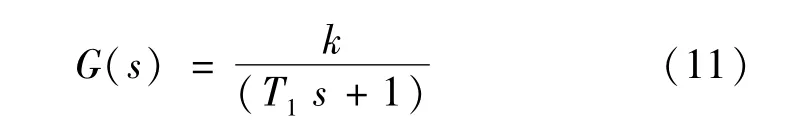
3.2 泰勒级数展开近似

当滞后时间常数τ较小时，若系统中含有惯性环节，一般认为τ小于惯性时间常数的0.3倍时，有

式（12）可以近似为：

3.3 多个小惯性时间常数合并

当惯性时间常数满足T1，T2≪T3，令TΣ=T1+T2，高阶系统

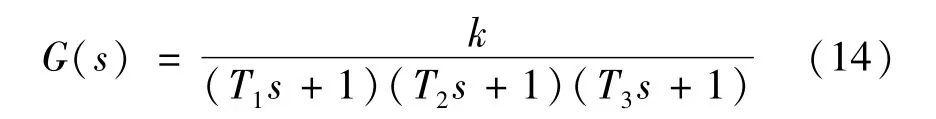
可以近似为二阶系统

3.4 多阶小惯性环节中高阶项忽略

当a，b≪c，且bc＞a时，高阶系统

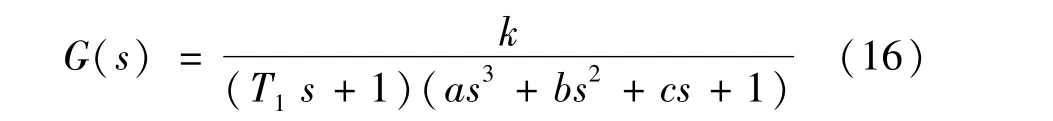
可以近似为二阶系统

3.5 模型结果验证

工程中高阶系统闭环传递函数为：

该4阶系统具有一个闭环零点z1=-2.1，一堆共轭复数主导极点s1，2=-0.5±j0.866，非主导极点s3=-2，s4=-8实部的模比主导极点实部模大3倍以上，零极点分布图如图5（a）所示，故该4阶系统可近似成：

运行Matlab得到原四阶系统及近似二阶系统的单位阶跃响应曲线分别用实线和虚线表示［见图5（b）］，得到的仿真结果见表2。通过主导极点求取的响应曲线与近似欠阻尼二阶系统的响应不完全一致，但结果基本正确，可用作高阶系统的近似分析。

表2 高阶系统动态性能比较

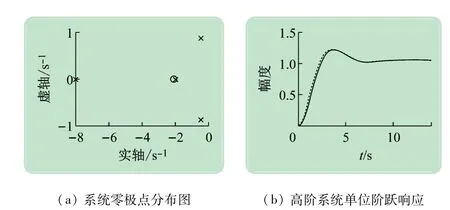
图5 高阶系统的模型验证结果

4 工程思想分析与课程思政

从欠阻尼二阶系统和双惯性环节的过阻尼二阶系统的数学模型可见，不同类型、不同元件组成、不同功能的物理对象可以具有完全相同形式的数学模型，这类物理系统被称为相似系统。相似系统揭示了不同物理现象间相同的数学本质，有利于工程技术人员使用简单系统去研究与之相似的复杂系统，也为控制系统的计算机数字仿真提供了基础。

无论是控制系统建模的思想，还是系统模型简化的方法，甚至是相似系统概念的提出，都一直在强调抓住系统的主要矛盾，忽略次要因素，这也反映出哲学中的解决矛盾问题的思想。有了相似系统这一概念，当工程技术人员已经熟悉某一工程系统的模型、特性及控制方法后，若在其他工程领域遇到与之数学规律相似的系统，可以将之前的知识与经验再一次应用到新系统中，但不可忘记矛盾还具有特殊性，在普适控制方案的基础上理论联系实际，具体问题具体分析，仔细论证，认真调试，做到真正意义上的举一反三。

此外，针对白箱、灰箱及黑箱3类系统进行建模时，还涉及建模方法选取、忽略哪些因素的问题，需要从两方面剖析。①不同的建模方法既有其有效性，也有其局限性，不是固定不变的。②系统的建模只能帮助工程设计人员理解系统的整体运行机制，但不能确保工程设计人员对系统认识的精准性和全面性，因此，不可一叶蔽目，需要统观全局，综合评定。

5 结语

将工程实践中的关联实例引入自动控制原理课程教学中，针对二阶系统的若干典型案例进行展开，将理论知识和实际系统结合起来，在教学中恰当地运用关联教学方法，不但能充分发挥教学的有效作用，而且也能使学生达到事半功倍的学习效率，加深对控制理论的理解和认识，同时有助于培养学生分析问题和解决问题的工程综合能力，拓宽学生的专业面和知识面，为以后的深入学习与工作打下良好、扎实的基础。