Up-conversion detection of mid-infrared light carrying orbital angular momentum
Zheng Ge(葛正) Chen Yang(杨琛) Yin-Hai Li(李银海) Yan Li(李岩)Shi-Kai Liu(刘世凯) Su-Jian Niu(牛素俭) Zhi-Yuan Zhou(周志远) and Bao-Sen Shi(史保森)
1CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China
2CAS Center for Excellence in Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China
Keywords: nonlinear optics,frequency up-conversion,mid-infrared detection
1. Introduction
The mid-infrared(MIR)band covers the absorption spectra of many molecules[1]and is closely related to the thermal radiation of objects, which has been used in many aspects, such as environmental monitoring,[2–4]geology for mineral identification,[5]stand-off detection,[6]and biomedical science.[7–10]Among them, the 3–5 μm band corresponds to one of the atmospheric communication windows,which is of potential importance in remote sensing[11]and communications.[12,13]On the other hand, light that carries orbital angular momentum (OAM) has stimulated considerable research interest in both the classical and quantum optical domains.[14–21]This particular beam with an azimuthal phase exp(ilφ) is well known as possessing an exact OAM ofl¯hper photon,[22]wherelandφrefer to the topological charge (TC) and azimuthal angle, respectively. MIR light that carries OAM is of great value in many specific applications, such as enhancing the information channel capacity in communications[23–25]and helping the understanding and formation of chiral microstructures.[26,27]In contrast, the detection equipment in the MIR band is not mature at present, reflecting on the lower detection sensitivity, higher noise, and narrower bandwidth compared with its visible or near-infrared(NIR)counterpart. Consequently,it is more effective to detect MIR light after converting it into visible/NIR light, utilizing high-performance detectors based on wide bandgap materials like Si.[28]Due to the high effective nonlinear coefficient and elimination of the walk-off effect, the quasi-phase-matching(QPM)technique has been used extensively for frequency conversion of light carrying OAM in previous works.[29–31]Up to now,the effective up-conversion of MIR light has been realized by using a waveguide.[32,33]However, compared with traditional bulk crystals,the loss of spatial information makes waveguide-based up-conversion unable to meet a wider range of detection requirements. In addition, current waveguidebased nonlinear transformation is mainly in the single-mode case,while higher-order mode frequency conversion still faces some difficulties.Bulk crystals have been widely used in many practical applications of frequency conversion because they can keep the phase and spatial information during the nonlinear process.[34–40]In this case,however,the beam waist radius in the center of the crystal is larger than that in a waveguide,which requires a much higher pump power to improve the quantum conversion efficiency (QCE). In previous works on MIR up-conversion detection,cavity-enhanced[41,42]or pulsed light pumped[43–45]systems were employed, achieving satisfactory QCE. However, a systematic study of the frequency conversion of OAM modes in the MIR band has not been reported to date.
In this work, the cascaded frequency conversion of light carrying OAM from 792 nm to 3100 nm and back to 792 nm was demonstrated, pumped by high power continuous-wave(CW) light. The laser light at 3100 nm was generated from a difference frequency generation (DFG) process, serving as the MIR source. Two identical MgO-doped periodically poled lithium niobate (MgO:PPLN from Covesion Ltd.) bulk crystals were utilized in the nonlinear processes above, each of which has a length of 40 mm and has nine poling periods ranging from 20.9 μm to 23.3 μm in steps of 0.3 μm. With the temperature of the crystals controlled, the nonlinear processes satisfied the type-0 QPM condition. Here we used a channel with a poled period of 20.6 μm and an aperture of 0.5 mm by 0.5 mm. For the convenience of discussion,in both three-wave mixing processes,the respective wavelengths were defined asλs=792 nm,λp=1063.8 nm,andλi=3100 nm,satisfying the relation 1/λs=1/λp+1/λi. Based on the nonlinear coupling equations, we proposed an analytical expression in the un-depleted approximation, which described the up-conversion efficiencies for various OAM values. Meanwhile, in the case of the depleted condition, the results given by numerical calculations were presented and compared with the experimental results. The final power efficiencies realized for conversion from MIR to visible are 133.1%, 40.7%,and 13.6% for TC ofl=0, 1, and 2, respectively, and the corresponding maximum QCEs are 34.0%,10.4%,and 3.5%.We also showed that the OAM is conserved in the conversion process. The high conversion efficiency and well-preserved phase information indicated that our primary study for MIR up-conversion is both reliable and useful, and will pave the way for further applications in remote sensing, high capacity optical communications,and image detection.
2. Theoretical model
The theoretical analysis for sum frequency generation(SFG), which is based on a second-order nonlinearity, is shown as follows. The nonlinear process involves the mixing of three waves, including a strong pump wave at frequencyωp, an idler wave to be converted at frequencyωi, and the up-converted beam at frequencyωs. In our experiment, the pump light is a normal Gaussian beam, while the idler light is in the OAM mode with a TC ofl. In the un-depleted pump approximation,the nonlinear coupled equations can be simplified as[46]
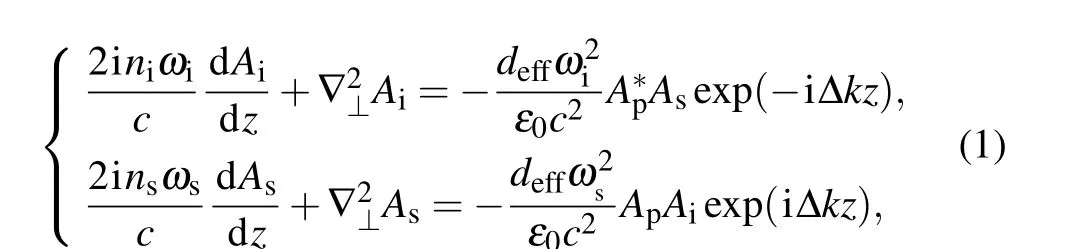
wheredeffis the effective nonlinear efficiency of the crystal;ε0is the permittivity of a vacuum;nj(j=p,i,s) are the refractive indexes inside the crystal and the subscripts correspond to the pump, the idler, and the signal light, respectively;Δk=ks-ki-kp+2π/Λis the phase mismatch in the SFG process andΛis the poling period of the crystal;andAj(j=p,i,s)are the electrical fields of the pump, the idler and the signal beams,respectively,which can be expressed as[47]

wherenj(j=p,i,s)are the refractive indexes of the pump,the idler, and the signal beams inside the crystal;ω0j(j=p,i,s)are the beam waists;Z0j=πnjω20j/λj(j= p,i,s) are the Rayleigh ranges of these beams;lrefers to the value of TC and is equal to zero in Gaussian mode; andφ=tan-1(y/x).We have directly omitted the term containing Gouy phase shift here, which can be ignored since the two input beams have approximately matching phases according to our experimental conditions. When considering the slowly varying amplitude approximation and the un-depleted pump approximation,an analytical expression of the SFG power can be obtained as follows:[48]
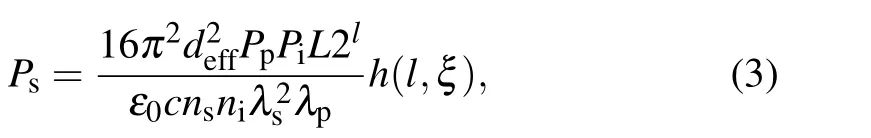
whereLis the length of the crystal;Pj(j=p,i,s) are the pump,the idler,and the signal power of these beams,respectively;andh(l,ξ)is the focusing function defined as
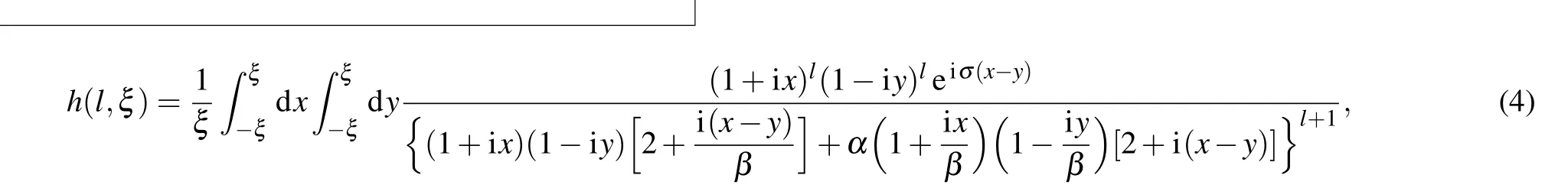
ξ=L/bpis defined as the focusing parameter of the pump beam, wherebp= 2Z0pis the confocal parameter;α=w20s/w20pandβ=bi/bpare determined by the waist ratio of the two beams; andσ= Δkbp/2 is the phase-mismatching parameter. Obviously, the loss of both pump light and input idler light is ignored when obtaining the analytical expressions,which may produce deviations in specific experiments.More discussion will be presented in the subsequent analysis of the experimental results. Therefore, numerical simulation was also conducted based on the coupled wave equations,utilizing a technique called the split-step Fourier method.[49,50]The basic assumption here is that spatial evolution and nonlinear effects can act separately for each small distance traveled by the light field during transmission. In this case,the transfer process fromztoz+dzcan be carried out in two steps. In the first step,only non-linear effects are considered in Eq.(1),which gives
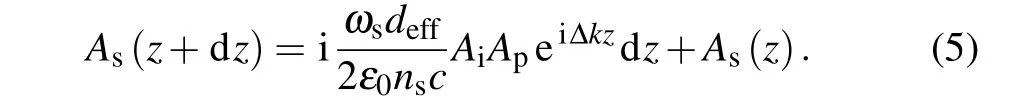
In the second step, there is only space evolution, and the Fourier transform term of the light field satisfies the following relation:
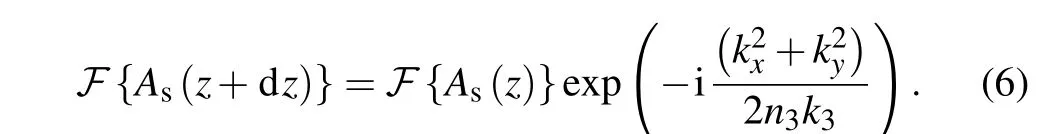
With this method,we obtained a series of discrete points after setting the initial conditions, showing the intensity variations of the idler and signal light at different positions in the crystal for Gauss mode, as shown in Fig. 1. Obviously, the accuracy of the simulation depends on the choice of step size,which also affects the speed of the calculation. An important advantage of the split-step Fourier method is that it simulates the beam mode field evolution process,which is useful for analyzing the effect of beams overlapping on the non-linear efficiency. Taking the signal light in Gauss mode and OAM mode withl=2 as examples,we showed in Figs.1(b)and 1(c)the predicted normalized efficiency at different beam waists,helping to find the best focusing parameters for subsequent experiments.
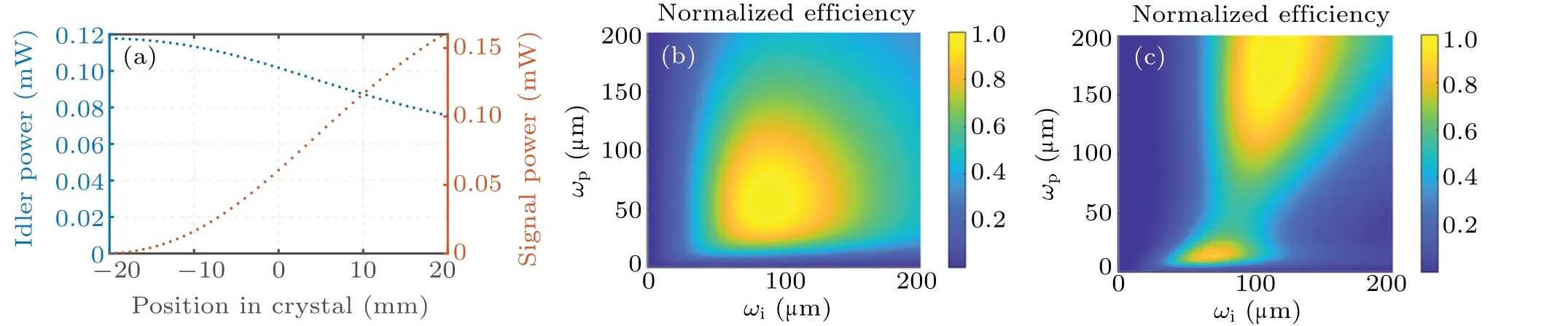
Fig. 1. (a) Dependence of the powers of the idler and signal beams on the propagation distance inside the nonlinear crystal. (b) and (c) Normalized efficiency with different beam waists for l=0 and 2.
3. Experimental setup
The schematic of the experimental setup is illustrated in Fig. 2. The signal beam for the down-conversion came from a diode laser (TOPTICA pro, Graefelfing); its spatial mode was later optimized by passing through a single-mode optical fiber. The pump beam was provided by an Yb-doped fiber laser working at 1064 nm, enhanced by a fiber amplifier, and then separated into two channels,pumping the DFG and SFG modules, respectively. Each laser beam was set to vertical polarization by the wave plates before the nonlinear crystal,satisfying the restriction of the phase-matching condition. A vortex phase plate(VPP)was placed before the focusing lens,imprinting OAM on the signal beam.
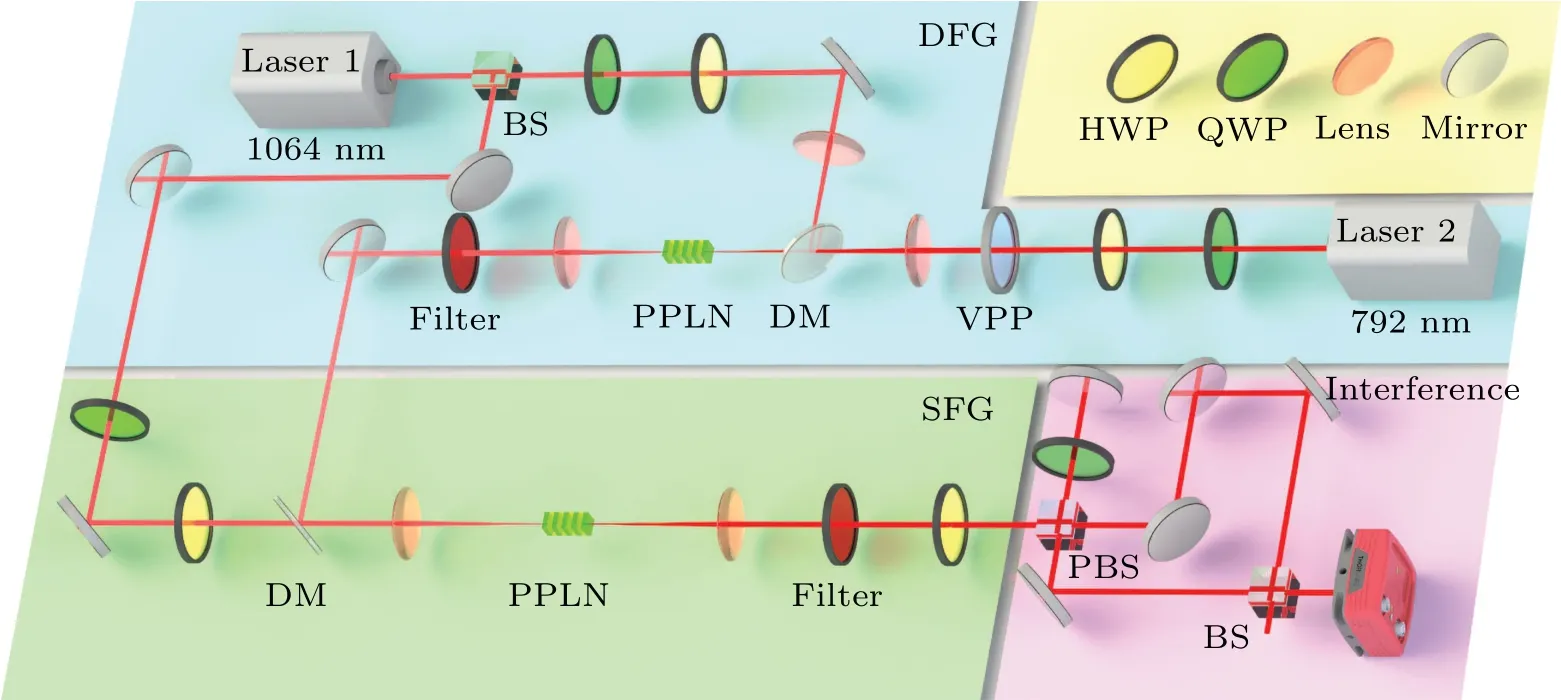
Fig.2. Experimental setup. VPP:vortex phase plate;DM:dichromatic mirror;BPF:band-pass filter;PPLN:periodically poled lithium niobate crystal;HWP(QWP):half-wave plate(quarter-wave plate);PBS(BS):polarization beam splitter(beam splitter);CCD:charge-coupled device camera.
In the first crystal, the waist sizes for the pump and the signal beams were 43 μm and 37 μm at the focus, respectively. The temperature of each crystal was controlled using a homemade semiconductor Peltier temperature cooler,the temperature stability of which is±2 mK.At the end of the DFG module,a long-pass filter removed the pump and signal beam,before the idler beam was measured by a mercury telluride detector(MCT).In the second frequency conversion process,the pump and idler beam overlapped after a dichromatic mirror,focused by the lens with beam waists of 65 μm and 110 μm,respectively. The filter after the SFG crystal removed all the off-target beams except the up-converted beam at 792 nm before it entered the interference module.The input light with an OAM state of|l〉was converted into the form of|l〉+eiφ|-l〉by a specially designed balanced interferometer, as discussed in our previous work.[51]The result of the interference presented a petal-like pattern and was captured by a chargecoupled device camera placed on the output side. The petals had a count of exactly 2l, which signified that the value of the TC carried by the generated beam can be found by simply analyzing the patterns.
4. Results and discussion
In the first DFG module, both the input beams we used had a power of 1 W, preparing a 3100 nm Gaussian beam with a power of 2.36 mW. For ease of comparison, the idler power was adjusted to 0.2 mW with an optical attenuator for different OAM. The final power of the wave to be converted was 0.118 mW at the incident face of the crystal, suffering a total loss of 41.1%during the transmitting procedure,which was mainly introduced by the dichromatic mirror because of the mismatch of the center wavelength. For varying up-conversion pump power (while the idler power was maintained at 0.118 mW), the results of the generated signal power for each OAM are illustrated in Fig. 3(a). Notice that the results given by the analytical calculations agree well with the experimental values initially, but gradually deviate as the pumping power increases. This deviation is not a surprise,as the small-signal approximation was used in obtaining the analytical expressions, which requires a low conversion efficiency. As the pump power increased, the consumption of MIR photons intensified and deviations between theoretical and experimental results were inevitable. The numerical calculation,on the other hand,avoided this problem and gave theoretical predictions that are relatively close to the experimental values. For both thel= 1 and 2 cases, there was some deviation between the theoretical and experimental values. Because the Gaussian light passing through the VPP was not in an exact Laguerre Gaussian mode,[52,53]aberration of the MIR beams carrying OAM generated by the DFG progress was unavoidable.Considering the 2.03%power loss caused by the subsequent filter,the power efficiencies of the SFG system determined usingηpower=P792/P3100were 133.1%, 40.7%,and 13.6% for TClvalues of 0, 1, and 2 respectively with a pump power of 37 W,and the corresponding QCEs defined byηquantum =ηpowerλ792/λ3100were 34.0%, 10.4%, and 3.5%.The conversion efficiency was satisfied in Gauss mode but reduced rapidly for increasing OAM orders. The main cause was different overlaps between the idler and the pump beams,as the OAM charge would affect the beam size and amplitude vividly. Consequently,in the up-conversion of structured beams with different OAM modes, the focusing parameters can be adjusted utilizing the same method shown in Figs.1(b)and 1(c),which would optimize the efficiency of SFG to some extent. To further eliminate the dependence of the conversion efficiency on the TC,modulation methods such as flat-top pump or imaging techniques can be considered.[54,55]
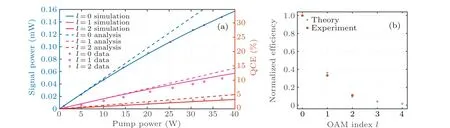
Fig. 3. Experimental results and theoretical predictions of the up-conversion process. (a) Relationships between the pump power and the SFG output powers for l =0, 1, and 2. The dashed lines are the analytical projections based on Eq. (3), while the solid lines present the results of numerical simulation. (b)Experimental results and predictions from numerical simulations of up-conversion efficiency for different OAM indexes.
During the two-step frequency transformation,the OAM should always be conserved as described in our previous study.Take the SFG process as an example,assuming that the two input beams carried TC ofl1andl2respectively, the generated SFG light would have OAM of(l1+l2)¯h.[51]In the DFG process, one of the input light carried the OAM withl, so the resulting MIR and up-converted light should both carry OAM with the same TC. Based on the above theoretical analysis,the experiment result can be well explained now. The intensity distributions of the signal beam withl=1 and 2, shown in Figs. 4(a)and 4(c), were recorded by blocking one arm of the interferometer,and the output images of the interferometer in normal operation are shown in Figs. 4(b) and 4(d). Figures 4(e)–4(h) give the corresponding simulation results for Figs.4(a)–4(d), exhibiting the same characteristics as the experimental results. The petal-like interference pattern shows the mode indices of the generated beam, as discussed in the preceding presentation. The numbers of petals in our experimental results indicated that the TCs of the up-converted light were 1 and 2 respectively,equaling the TC of the original signal beam,which is in agreement with the theoretical prediction and numerical simulations.

Fig.4. Experimental results of the up-converted images. (a)and(c)Intensity distributions of up-converted light for l=1 and 2. (b)and(d)Interference patterns for l=1 and 2. (e)–(h)Images of the corresponding simulation results for(a)–(d).
The dependence of output power on the temperature of the crystal for the DFG and SFG processes is shown in Fig.5.The phase-matching temperatures were 55°C and 55.2°C,while the temperature bandwidths were 7.2°C and 6.9°C,respectively. The experimental results of the power of the generated 3100 nm and 792 nm waves with different temperatures are marked in the figure,and the measured data can be fitted by solving the coupled wave equations.[46]The insert in the upper right corner of Fig. 4 shows how the phase mismatch affects the efficiency of SFG by numerical simulation, displaying a half peak width of 140 m-1, while the same parameter given by the experimental conditions is 137 m-1.
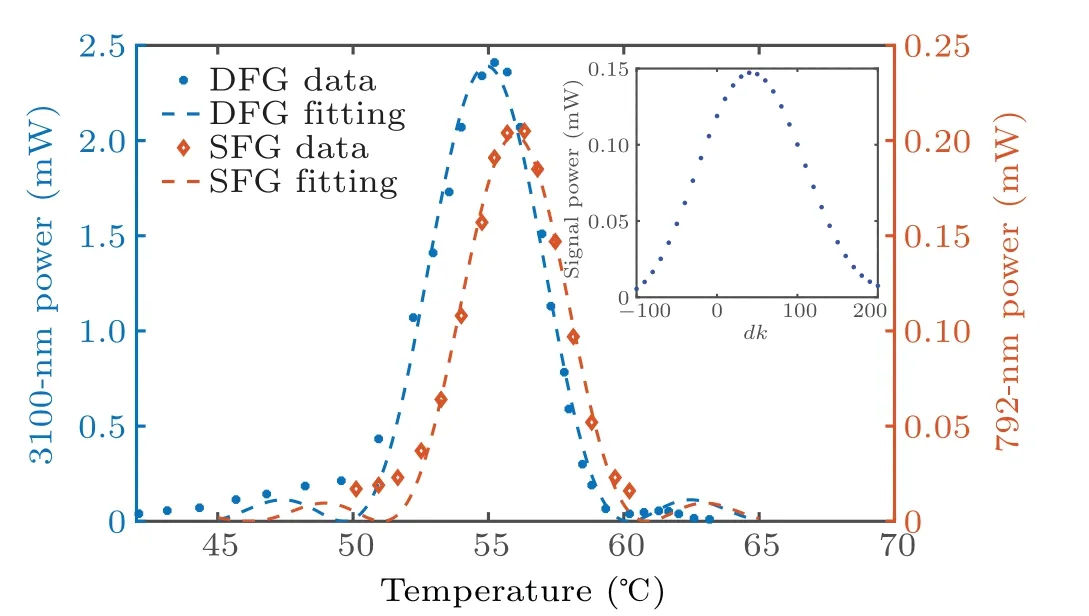
Fig.5. Output power of DFG and SFG depending on temperature.
5. Conclusion
Based on our present experimental conditions,the intensity profile of the MIR beam could not be obtained directly.The length of the crystals and the internal nonuniformity affected the quality of generated beams to a certain extent,such as the generation of distortions and vortex splitting caused by aberration. Besides,the relatively small aperture of the crystal puts a limit on the choice of the focusing parameter,especially for a beam at a long wavelength. For up-conversion of image or light carrying OAM with higher-order TC,a crystal with a larger intersecting surface would perform better.
In summary, we have studied the frequency bridge between the visible and MIR bands for vortex light based on QPM crystals. We generated the MIR beams through a DFG process and then demonstrated OAM frequency up-conversion experimentally for different OAM modes. The maximum QCEs that were achieved for OAM modes with TCs of 0, 1,and 2 were 34.0%, 10.4%, and 3.5%, respectively. The experimental data were compared with the results of analytical expression and numerical simulation, proving the feasibility of theoretical prediction. We also verified the conservation of OAM in cascaded processes and studied the dependence of the output power on the temperature of the crystals. The present work provides a reliable solution for up-conversion detection of light carrying OAM in the MIR band, using a bulk crystal that preserves phase information well. By adjusting the crystal parameters and reducing the noise,this setup could potentially be extended to general image up-conversion detection and works at the single-photon level. This progress will be beneficial and encouraging for numerous applications that use MIR light as an information carrier and a means of detection,for example in the fields of biological detection,astronomical observation,[56]environmental monitoring, and remote sensing.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 92065101 and 11934013) and Anhui Initiative In Quantum Information Technologies(Grant No.AHY020200).
- Chinese Physics B的其它文章
- Design of vertical diamond Schottky barrier diode with junction terminal extension structure by using the n-Ga2O3/p-diamond heterojunction
- Multiple modes of perpendicular magnetization switching scheme in single spin–orbit torque device
- Evolution of the high-field-side radiation belts during the neon seeding plasma discharge in EAST tokamak
- Phase-matched second-harmonic generation in hybrid polymer-LN waveguides
- Circular dichroism spectra of α-lactose molecular measured by terahertz time-domain spectroscopy
- Recombination-induced voltage-dependent photocurrent collection loss in CdTe thin film solar cell

