Measurement-device-independent quantum secret sharing with hyper-encoding

Xing-Xing Ju(居星星) Wei Zhong(钟伟) Yu-Bo Sheng(盛宇波) and Lan Zhou(周澜)

1College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China

2College of Electronic and Optical Engineering&College of Flexible Electronics(Future Technology),Nanjing University of Posts and Telecommunications,Nanjing 210023,China

3Institute of Quantum Information and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Keywords: measurement-device-independent quantum secret sharing,hyper-encoding technology,cross-Kerr nonlinearity,hyper-entangled Greenberger–Horne–Zeilinger state analysis

1. Introduction

Quantum communication is an important branch of quantum information. Quantum communication has unconditional security, which is based on the basic principles of quantum mechanics. Quantum communication begins with the research on quantum key distribution(QKD),which was first proposed by Bennett and Brassard in 1984.[1]QKD can distribute secure keys between two remote participants.[2–17]Besides QKD,there are some important branches in the field of quantum communication,such as quantum secret sharing(QSS),[18–33]and quantum secure direct communication(QSDC).[34–49]

QSS was first proposed by Hilleryet al.in 1999[18]based on quantum technology and traditional cryptographic sharing technology. In QSS protocols, the key sender (dealer) splits a key into several parts and distributes each part to a participant. The participants can read out the key only when they cooperate with each other. Conversely, all the participants can also cooperate to distribute a secure key to the dealer.[20]In 2004,Xiaoet al.[22]proposed a multi-party QSS protocol using the Greenberger–Horne–Zeilinger(GHZ)state.By choosing an asymmetric measurement basis, their protocol can be 100% efficient. In 2005, based on a QSDC protocol, Zhanget al.[23]proposed a (n,n)-threshold multiparty QSS scheme using single photons. In 2014,Bellet al.[25]reported an experimental demonstration of the graph state-based QSS.They showed that one can reliably encode,distribute and share quantum information among four parties with the graph state. In practical applications, there are some attack modes focusing on imperfect measurement devices,such as the fakestate attack,[50]time-shift attack,[51,52]and detection blinding attack.[53]Researchers proposed the measurement-deviceindependent (MDI) technology, which can resist all possible attacks from the imperfect measurement devices.[54–63]In 2015,Fuet al.proposed the first MDI-QSS protocol encoded in the polarization degree of freedom(DOF).[56]However,the key generation rate of the original MDI-QSS is relatively low.Hyper-encoding,which means encoding in two or more DOFs of a single photon,is an effective way to increase the channel capacity of single photons.Recently,the hyper-encoding technology has been widely adopted in the MDI-QKD and MDIQSDC protocols to increase the key generation rate and secure message capacity,respectively.[63–66]

In this paper, we propose a hyper-encoding MDI-QSS protocol. In this protocol,the dealer and the other two participants generate polarization-spatial-mode hyper-encoded photon qudits and send the photons to the forth party. The forth party makes the hyper-entangled GHZ state analysis(HGSA)constructed with the cross-Kerr nonlinearities,which can completely distinguish all the 64 hyper-entangled GHZ states.With the hyper-encoding and HGSA, our hyper-encoding MDI-QSS protocol can achieve higher key generation rate and extend the communication distance. This hyper-encoding MDI-QSS has potential applications in the field of quantum communication in the future.

This paper is organized as follows. In Section 2, we explain our hyper-encoding MDI-QSS protocol in detail. In Section 3, we analyze the security of the hyper-encoding MDIQSS protocol and simulate its key generation rate. In Section 4,we give some discussions and draw a conclusion.

2. The hyper-encoding MDI-QSS protocol

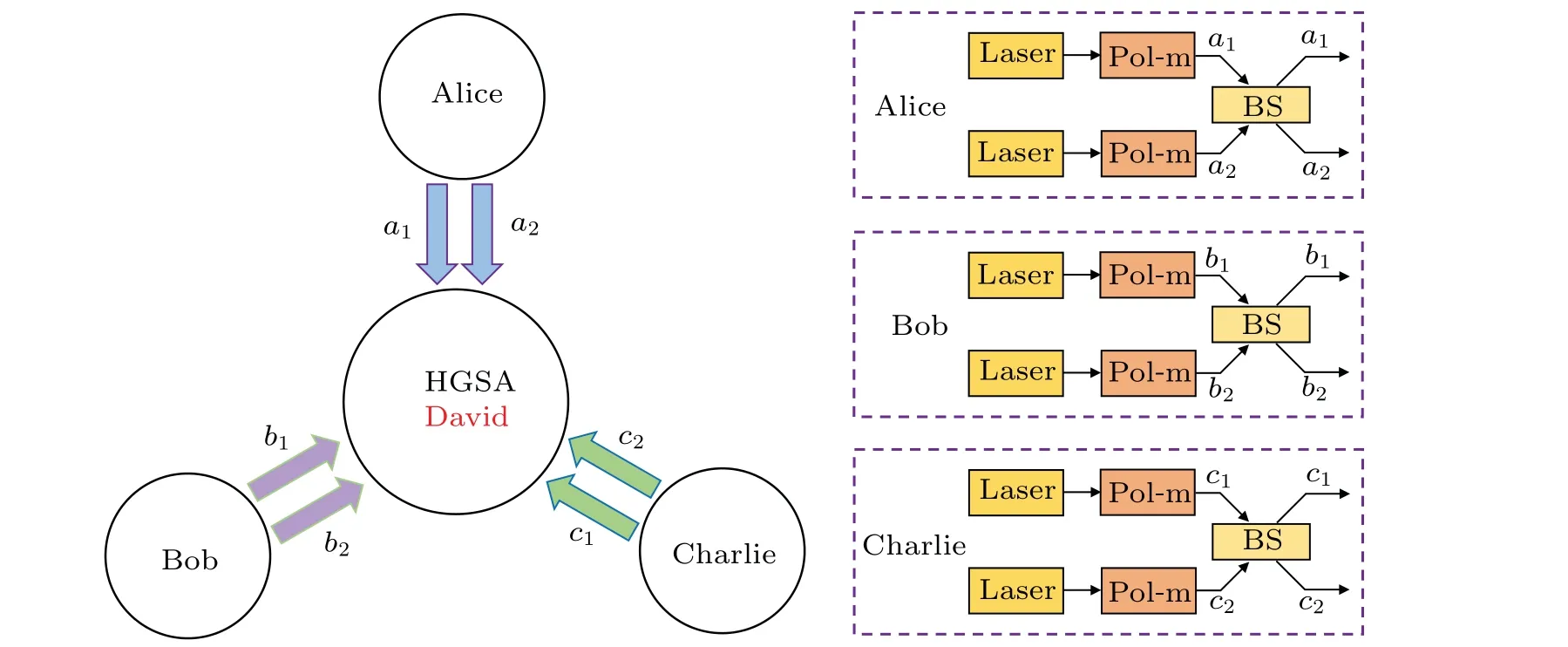
Fig.1. Illustration of the hyper-encoding MDI-QSS protocol. Alice,Bob and Charlie separately prepares phase-randomized weak coherent pulses(WCPs) in BB84 polarization states. The polarization modulator (Pol-M) controls the encoding in the polarization DOF, while the 50:50 beam splitter (BS) controls the encoding in the spatial-mode DOF. Our protocol adopts the hyper-entangled GHZ state analysis (HGSA) technique proposed in Ref.[64]to completely distinguish the 64 hyper-entangled GHZ states. Here,i1 and i2 (i=a,b,c)mean different spatial modes.

Figure 1 illustrates the basic principle of our hyperencoding MDI-QSS protocol,which proceeds as follows.

Step 1 The dealer Alice, and the other two parties Bob and Charlie randomly selectZbasis orXbasis in polarization and spatial-mode DOFs to generate a series of single photon qudits. In detail,the three parties first prepare single photons in BB84 polarization states with the help of polarization modulator(Pol-M).In the spatial-mode DOF,if one wants to generate a photon in theZbasis, he can directly generate the photon in the corresponding spatial mode. If he wants to generate a photon inXbasis,he uses the 50:50 beam splitter(BS),which can make|a1〉→|+〉aS(|b1〉→|+〉bS,|c1〉→|+〉cS)and|a2〉→|-〉aS(|b2〉→|-〉bS,|c2〉→|-〉cS). Then,they send the photons to a forth party David locating in the middle node of the quantum channels. Here,it should be noted that David can be untrustworthy,or even completely controlled by the eavesdropper.

Step 2 When David receives the photon qudits, he performs the HGSA on the photons. Here, we adopt the HGSA protocol in Ref. [67], which can completely distinguish all the possible hyper-entangled GHZ states with the help of the cross-Kerr nonlinearity. The GHZ states in the polarization and spatial-mode DOFs can be written as

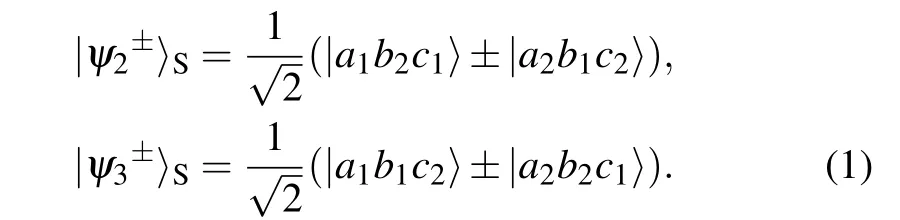
Step 3 Alice,Bob,and Charlie announce the generation basis of each photon qudit in both DOFs. If the three photons for the HGSA are generated in different bases in a DOF,the HGSA result and their encoding in this DOF should be discarded. On the other hand, if the three photons are generated in the same basis in a DOF, the HGSA result and their encoding information in this DOF will be retained. When all the parties chooseXbasis in a DOF,the encoding information in this DOF would be used to generate the original key. Tables 1 and 2 provide all the possible GSA results and Alice’s key in the polarization and spatial-mode DOFs when the three parties use the same basis, respectively. When all the parties chooseXbasis in a DOF,Bob will publish his own encoding information in this DOF.We take the polarization DOF as an example. If the measurement result is|ψ+y 〉P(y=0,1,2,3),the encoding relationship isXA=XB ⊕XC. On the other hand,if the measurement result is|ψ-y 〉P(y=0,1,2,3), the encoding relationship isXA ⊕1=XB ⊕XC. As a result,Charlie can infer Alice’s encoding information in the polarization DOF as the original key. The rule in the spatial-mode DOF is the same as that in the polarization DOF.

Table 1. Possible GSA results and Alice’s key in the polarization DOF when all parties use the same basis.

Table 2. Possible GSA results and Alice’s key in the spatial-mode DOF when all parties use the same basis.

Step 4 The three parties repeat steps 1–3 until Charlie obtains sufficient number of original keys.

Step 5 When Alice, Bob and Charlie all chooseZbasis in a DOF, they will publish their encoding information in this DOF to make the security checking. A bit error happens if the measurement result is not the possible results shown in Tables 1 and 2. As a result,they can calculate the quantum bit error rate (QBER) in both DOFs. If the QBER of any DOF exceeds the tolerant threshold,they ensure that the key generation is not secure and discard all the generated original keys.In contrast, if the QBERs in both DOFs are lower than the tolerant thresholds, they will ensure the security of the key generation and retain the original keys.

Step 6 Alice, Bob and Charlie perform error correction and private amplification to form the final secure keys.

3. The security analysis and key generation rate of the hyper-encoding MDI-QSS protocol

In this section,we provide the security analysis and simulate the key generation rate of our hyper-encoding MDI-QSS protocol.In our protocol,as all the measurement tasks are performed by the forth party, the protocol can resist all possible attacks from the measurement devices. Its security proof is similar to that of the original MDI-QSS protocol[56]and MDIQKD protocol.[54]Here, we have to consider the attack from the forth party David, who can be untrustworthy and totally controlled by Eve. In the first case, if David announces the wrong HGSA results, his dishonesty may make Charlie obtain wrong keys. However, his dishonest behavior would increase the QBER in both DOFs,and thus can be checked out by the security checking. It is worth noting that at the step 3 of the protocol, when all three parties chooseXbasis, only Bob publishes his encoding information. As Charlie does not announce his encoding information,Eve(David)cannot infer Alice’s key even though he can obtain HGSA results. As a result,the forth party cannot cause the key leakage.

Then, we analyze the key generation of the hyperencoding MDI-QSS protocol.According to the basic selection principle in each DOF,there are totally three different cases.

Next, we make a numerical simulation of this hyperencoding MDI-QSS protocol’s key generation rate under practical experimental condition. Based on previous experimental parameters given in Refs.[68,69],we assume that Alice(Bob,Charlie)uses the common WCP sources,in which the photon number follows the Poisson distribution with an average ofμa(μb,μc). The forth party locates in the middle of three parties with the distance between the forth party and any party beingd. In this way, the channel transmission efficiency ista=tb=tc=10-αd/10,whereα=0.2 dB/Km for a standard optical fiber. Based on Ref.[55], we setμa=μb=μc=0.3 and consider the total polarization and spatial-mode misalignment error rates asemP=emS=1.5%.

According to the original MDI-QSS protocol encoding in polarization DOF,[56]the key generation rate of the MDI-QSS protocol encoding in the polarization DOF can be written as

Figure 2 provides the key generation rateRtof our hyperencoding MDI-QSS protocol versus the photon transmission distancedfrom any party to the forth party. Based on the hyper-encoding technology, the parties can generate keys independently in both DOFs. Meanwhile, with the help of the QND gate constructed with the cross-Kerr nonlinearity, we can completely eliminate the influence from the multi-photon emission and the vacuum state emission, and reduce the total gain and total error rate in both DOFs. As a result,our MDIQSS protocol does not require the decoy state method. The above features can efficiently increase the key generation rate and extend the photon transmission distance. Under the photon transmission distanced=100 km,Rtcan achieve about 5.4×10-9, which is about three orders of magnitude higher than that of the original MDI-QSS protocol.[56]

Fig. 2. Total secure key generation rate of our hyper-encoding MDIQSS protocol altered with the photon transmission distance d from any party to the forth party. Here,we suppose that the average photon numbers of the WCP sources satisfy μa=μb=μc=0.3.The misalignment error rates in both DOFs meet emP =emS =1.5%. The inherent efficiency and error rate of the homodyne measurement are ηl =0.98 and ed =0.01, respectively. We also set the inefficiency function for the error correction process in both DOFs to be f =1.16.

4. Discussion and conclusion

In our hyper-encoding MDI-QSS, the high-dimension system comprises two independent subsystems. The two subsystems can be manipulated and measured independently to generate the key, which can effectively increase the key generation rate of our MDI-QSS protocol. Moreover,if the GSA in a DOF fails but the GSA in the other DOF is successful,the parties only need to discard the key encoded in one DOF but still retain the coding information in the other DOF to generate the key. Meanwhile,an error in a DOF does not influence the coding information in the other DOF,which can still be used to generate the key. As a result,the hyper-encoding MDI-QSS protocol is quite flexible.

It is natural that our MDI-QSS protocol can be extended to arbitraryN-party MDI-QSS.In theory,Nparties require to randomly prepare a large number of polarization-spatial-mode hyper-encoded photon qudits. Then,they send the photons to the measurement party for performing theN-photon HGSA,which can completely distinguish all the possibleN-photon GHZ states in both DOFs. After the HGSA,the measurement party announces the results, andNparties announce the generation basis of each photon. They only preserve the GSA result when they generate the photon qudits in the same basis in a DOF. When all theNparties choose theXbasis in a DOF, their encoding bits would be used to generate the original keys. When they all choose theZbasis in a DOF, they will announce their encoding in this DOF to make the security checking. When the security is guaranteed, the parties will perform the error correction and private amplification to form the final secure keys.

Finally, we will briefly discuss the experimental realization of this MDI-QSS protocol. The complete HGSA is the key element of our MDI-QSS protocol. So far, the cross-Kerr is still a challenge in the experiment. The reason is that the natural cross-Kerr nonlinearity is quite weak, so that it is hard to discriminate the weak phase shift by the homodyne measurement. Fortunately, during the recent few years,the cross-Kerr nonlinearity has achieved great progress.[74–76]In 2016, Beck’s group experimentally obtained a cross-phase shift ofπ/6 between signal fields stored in an atomic quantum memory.[74]Later,D¨urret al.reached the strong interactions in the Rydberg electromagnetically induced transparency(EIT) experiments, which created a controlled phase shift of 3.3±0.2 rad by using the incoming pulses with an average of 0.6 photons.[75]In 2019,Sinclairet al.realized the cross-Kerr nonlinearity in a free-space medium based on the Rydberg atoms and EIT technology,where the phase shift is 8 mrad/nW of signal power.[76]Based on the above attractive progress,it is possible to realize the complete HGSA in the near future.

In summary, we have proposed a polarization-spatialmode hyper-encoding MDI-QSS protocol, in which all the three parties, Alice, Bob and Charlie, prepare photon qudits hyper-encoded in spatial-mode and polarization DOFs. They send their photons to the forth party to make the complete HGSA. After the complete HGSA, all the three participants announce the generation basis of their photons in both DOFs,and Bob also announces his codes in both DOFs. If all the three parties choose theXbasis in a DOF,Charlie can speculate Alice’s raw key in this DOF according to the HGSA result and Bob’s code. In the protocol, the parties can encode the keys in both DOFs independently. The measurement errors and imperfect operations in one DOF do not affect the key generation in the other DOF.Meanwhile,the HGSA in the protocol can completely distinguish all the 64 hyper-entangled GHZ states and the incoming number in each input mode,so that the influence from vacuum state emission and multi-photon emission can be eliminated. The above factors can efficiently increase the key generation rate of our MDI-QSS protocol. This hyper-encoding MDI-QSS protocol may have potential applications in the near future.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant Nos.11974189 and 12175106).