测量不确定度评定方法及应用分析

高维胜，羊衍富

(1.四川华丰科技股份有限公司，四川绵阳，621000；2.四川互连创新科技有限公司，四川绵阳，621000)

1 引言

在检测和校准过程中，由于测量误差的存在，被测量自身定义和误差修正的不完善，被测量的真值很难准确复现。一直以来，人们不断追求最佳方式估计被测量的值，用测量不确定度来评定测量结果的质量高低。在ISO17025标准“校准实验室与检测实验室能力的通用要求”中指明，校准实验室出具的每份证书或报告都应包括测量结果的不确定度说明；CNAS-CL01“检测和校准实验室能力认可准则”第7.6条款规定：开展校准的实验室，包括校准自有设备，应评定所有校准的不确定度，开展检测的实验室应评定测量不确定；RB/T214“检验检测机构资质认定能力评价”中第4.5.15条规定：检验检测机构应可在检验检测出现临界值、内部质量控制或客户要求时，需要报告测量不确定度；由此可见不确定度评定的重要性。正确理解测量不确定度的含义，掌握好测量不确定度的评定方法，对提高测试和校准质量水平，推动我国检测和校准事业的发展有着重要意义。

2 不确定度定义

2.1测量不确定度：表征合理的赋予被测量之值得分散性，与测量结果相联系的参数。

2.2标准不确定度：以标准偏差表示的测量不确定度。

2.3合成标准不确定度：由在一个测量模型中各输入量的标准不确定度获得的输出量的标准不确定度。

2.4包含因子(k)：为获得扩展不确定度，对合成标准不确定度所乘的数字因子。

2.5扩展不确定度：合成标准不确定度与一个大于1的数字因子的乘积。

2.6A类评定：用统计分析方法，算出实验室标准偏差。

2.7B类评定: 用非统计分析方法，估计标准偏差。

3 评定方法、流程及实例

3.1 测量不确定度评定方法

3.1.1 建立被测量的数学模型，并计算各分量的标准不确定度

3.1.1.1 被测量的数学表达式：

y=f(x1,x2……xn)

(1)

3.1.1.2 确定各分量中不确定度的来源，不确定度来源一般包括以下几方面的因素：

①测量人员的因素(从业经验等)；

②仪器仪表设备的因素(稳定性、误差及不确定度等)；

③测量及操作方法(各种规范规程及标准等)；

④测量环境(温度、湿度、电压及频率等)；

⑤测量样品(性能稳定性、样品代表性等)。

3.1.1.3 计算标准偏差：对同一被测量进行n次测量，表征测量结果分散性的量，用s表示，其公式如下：

(2)

3.1.1.4 计算各分量的标准不确定度

(3)

(4)

—△为测量值的可能区间，通常用仪表精度、最大允差、仪表校准时确定的扩展不确定度来确定；

—k根据概率分布类型及要求的概率P确定。通常是已知某扩展不确定度是某合成标准不确定度的倍数，或者通过概率分布表查得。常用概率分布表如下：

表1 正态分布表

3.1.1.5 期间半宽度△一般根据以下信息确定

① 以前测量的数据；

② 生产厂提供的技术说明书；

③ 校准证书、检定证书提供的数据；

④ 手册或某些资料给出的参考数据。

3.1.2 计算合成标准不确定度uC

(5)

3.1.3 计算扩展不确定度U

U=kuC(k为包含因子)

(6)

3.1.4 注意事项：

① 不确定度计算结果带有单位，与被测量单位一致；

② 不确定度计算结果按照只进不舍的原则进行数据修约。

3.2 专业实验室测量不确定度评定流程图

测量不确定度评定流程见图1。

图1 测量不确定度评定流程图

3.3 接触电阻测量不确定度评定实例

3.3.1 测量方法和数学模型

本次测量采用直流低电阻测试仪TH2515，根据GB/T 5095、GJB 1217A等标准要求，测试方法为通过接触电阻测试仪测出两端之间的电压降，由该电压降及测试电流计算得出两端的接触电阻阻值，数学模型为：R=RX。式中，RX为仪表显示值，测试电流为直流0.1A。

3.3.2 不确定度来源

由三个不确定分量构成：重复性测量引入的不确定度分量Ua，人员读书引起的不确定度Ub1，校准证书提供的仪器不确定度Ub2。

3.3.3 由重复性引入的A类不确定度评定

取某一固定样品，使用相同的测试电流测试，对应的接触电阻测试仪读数12次测量计算标准差得出；复测量12次，操作人员不变；每次测量完毕，保持样品状态与接线状态及部位不变，复位接触电阻测试仪然后重新测试，测量数据如下：

表2 直流0.1A接触电阻测试数据 (单位：mΩ)

3.3.4 B类不确定度评定

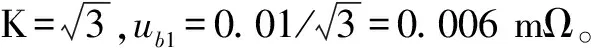
3.3.4.2 由校准证书可知，在测试电流为0.1A时，测试标准10mΩ，不确定度为0.01mΩ，包含概率为0.9545，查表得：K=2,ub2=0.01/2=0.005 mΩ。

3.3.5 合成标准不确定度uc

由于以上各分量互不相关，其测量得到合成不确定度可用方和根计算：

3.3.6 扩展不确定度U：

取p=0.95；则k=2，

则扩展不确定度：U=kuC=2×0.03=0.06 mΩ。

3.4 测量不确定度结果在合格评定中的应用

3.4.1 不确定度合格评定坐标的建立

图2 不确定度在合格评定中应用

3.4.2 合格评定中的几种判定情况

如图2，测量结果是否合格的各种可能情况则可以归纳为A、B、C、D、E、F、G、H等八种情况，这八种可能的情况，也可用表3表示。

表3 测量结果的8种可能情况

① D、H两种情况分别超出规定的误差上限和误差下限，故可判定它们均处于不合格状态；

② A、E两种情况均完全落在规定误差限内，故可判定它们均处于合格状态；

③ B、F两种情况的均值及分布的大部分落在规定误差限内，但有小部分情况超出规定的误差限，如判定测量结果合格，则有一定的“误判合格”的风险；

④ C、G两种情况的均值及分布的大部分落在规定误差限外，但有小部分情况落在规定误差限内，如判定测量结果不合格，则也有一定的“误判不合格”的风险；

4 结束语

本文根据作者在工作中的经验，总结出测量不确定度评定方法及结果在合格评定中的应用；测量不确定评定影响分量很多，在评定过程中，把握三不原则：“不遗漏”、“不重复”及“关注最大项”。遵守这三个原则，才能把不确定度评定准确，提升实验室的技术能力和专业水平，文中内容是作者的心得体会，若有不妥之处，敬请批评指正。