拉伸回弹法在碳纤维单丝压缩强度测试中的应用
王雪飞,李莹莹,钟俊俊,衡芳芳,时晓露,张永刚*,李德宏
(1.中国科学院宁波材料技术与工程研究所,浙江 宁波 315201;2.宁波新材料测试评价中心有限公司,浙江 宁波 315000)
碳纤维增强树脂基复合材料是由高分子树脂基体和碳纤维增强体复合而成的结构/功能材料,具有良好的力学性能、低密度、可设计、耐腐蚀、良好的使用性能等优点。碳纤维复合材料是量大面广的先进基础材料和制约制造业发展的关键战略材料,广泛应用于航空航天、轨道交通、能源电力、交通运输、运动器材等领域[1-2]。
复合材料构件在承受拉伸载荷的同时不可避免要受到压缩载荷的作用,低压缩强度及严重的压拉失衡(压缩强度与拉伸强度之比)使得复合材料容易在低压缩载荷下发生破坏,制约复合材料的应用,更难以满足装备性能提升的需求。为了提升复合材料的应用价值,必须提高碳纤维及其复合材料的压缩性能。
在碳纤维压缩性能研究中,首要解决的问题是碳纤维单丝压缩强度的准确评价。碳纤维直径小,施加轴向压缩应力时极易发生屈曲,压缩试验难度大增。碳纤维压缩强度的各种表征技术得到不断开发,至目前为止先后开发了弹性环法[3]、纤维单丝和束丝复合法[4-5]、弯曲梁法[6-7]、拉伸回弹法[8-9]和直接测量法[10-11]等方法。其中,直接测量法获得的数据最精确,但对仪器要求高,操作复杂;在弯曲梁法和纤维复合法中,纤维被包埋在树脂中,树脂及碳纤维/树脂界面等因素会影响测试结果,基体收缩产生的残余应力会极大影响测试结果;弹性环法中压缩应力在纤维截面上分布不均匀。与上述方法相比,拉伸回弹法尽管对压缩性能的检测不能直接给出压缩强度的结果,但是其制样方法简单,测试流程简便,经过多年发展后,解决了轴向压缩载荷加载问题,形成了压缩强度计算方法,能够获得可重复的结果。
针对拉伸回弹法在碳纤维压缩强度测试中的应用,作者从拉伸回弹法的测试原理和应用出发,简述了拉伸回弹试验中试样的制备及预加应力的获得方法,详细介绍了根据预加应力计算压缩强度的方法,并指出了影响纤维压缩强度的计算和实验因素,以期能够为碳纤维压缩强度测试提供指导,也为碳纤维在复合材料中的应用提供压缩性能的数据支撑。
1 拉伸回弹法的测试原理及影响压缩性能的结构因素
1.1 测试原理
拉伸回弹法最早由S.R.ALLEN于1987年提出[8]。在测试时,纤维试样首先被拉伸到设定的拉伸应力,被拉伸的纤维因此储存了等量的应变能;当纤维从中部断开时,会引发回弹效应;在纤维拉伸应力释放时,储存在纤维中的应变能转化为动能,应力波沿着纤维向夹持端移动;当应力波到达刚性夹持端后,动能又全部重新转换为应变能,由此引发的压缩应力沿着纤维轴向反向传播,当压缩应力超过纤维单丝的压缩强度时,靠近夹紧端的纤维段发生断裂。拉伸回弹法测试过程见图1。
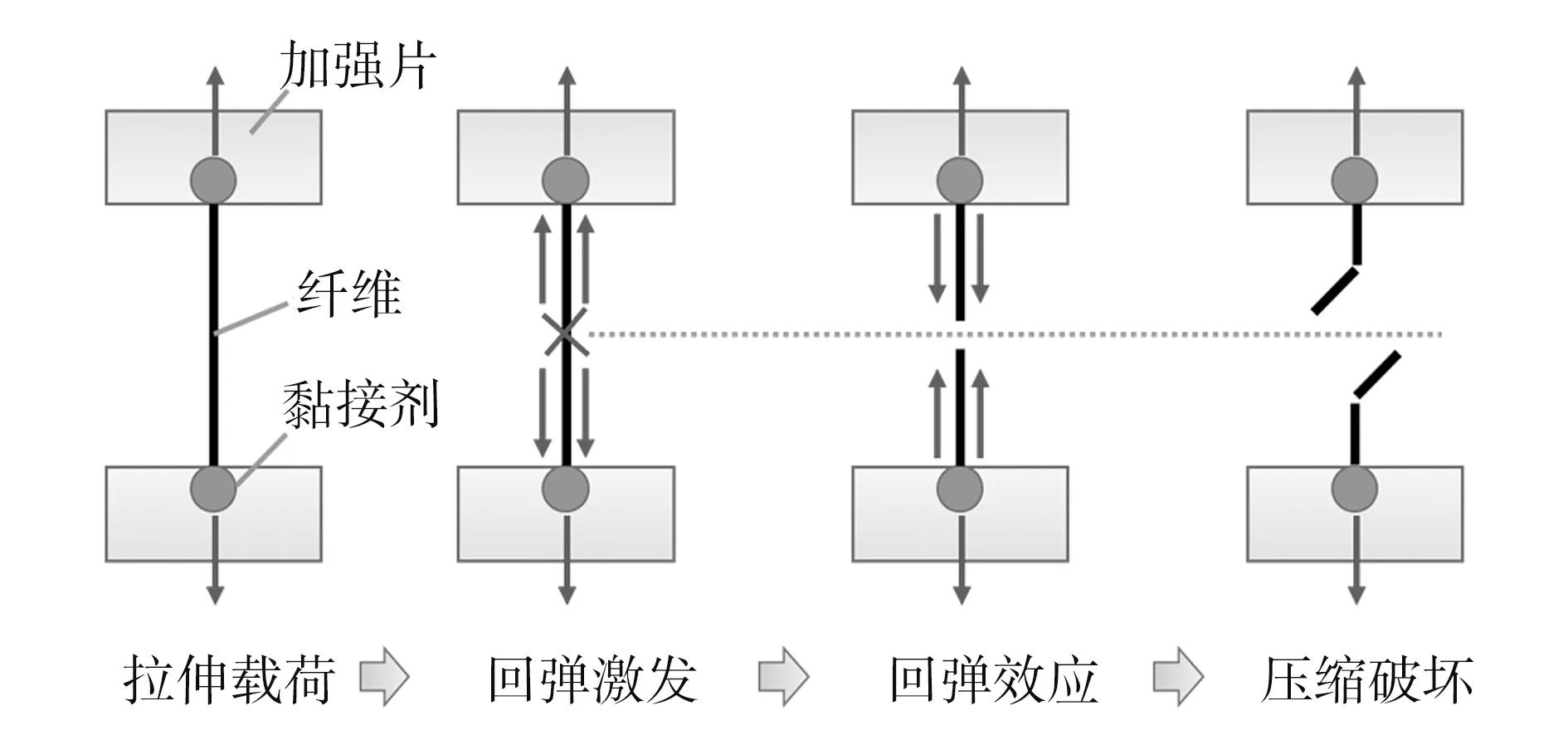
图1 拉伸回弹法测试过程示意
拉伸回弹法遵循以下假设:(1)纤维为线弹性材料,符合虎克定律;(2)标距两端均为刚性黏接;(3)在断裂瞬间纤维无初始速度;(4)在断裂瞬间,除了断裂处应力为零之外,纤维在轴向上具有均匀的拉伸应力分布。JIANG H等[11]通过对聚丙烯腈基碳纤维的回弹断裂形貌进行分析,认为回弹试验中压缩破坏除了来自轴向压缩应力,还可能来自原纤/微原纤的剪切和/或屈曲破坏。
1.2 影响压缩性能的结构因素
通过拉伸回弹法研究碳纤维的压缩性能,研究人员能够获知影响压缩强度的结构因素。G.J.HAYES等[12]对沥青基碳纤维的压缩强度进行研究,发现在各模量水平上折叠径向结构碳纤维比平层织构碳纤维具有更高的抗压强度,这主要归因于褶皱的径向织构抑制了基面的剪切。M.G.DOBB等[13]通过聚丙烯腈基和中间相沥青基碳纤维的微观结构特征与压缩性能分析,认为碳纤维的压缩强度受多种结构特性的综合影响,压缩强度随晶间和晶内无序量的增加而线性增加;对于给定的无序程度,微结构特征分布更均匀的纤维表现出更高的压缩破坏应力。为了提高纤维的压缩强度,应该将其微晶尺寸控制在5 nm以下,同时使其具有良好的取向[13]。石墨微晶晶格之间的强相互作用也能够提升纤维的压缩强度和剪切强度[11, 14]。
2 试样的制备与测试
2.1 试样的制备
碳纤维单丝压缩强度测试试样的制备可参考单丝拉伸强度测试试样的制备方法[14-15]。首先,在纤维试样中剪取一定长度的纤维束;然后,从纤维束中随机选择一根单丝,用合适的黏接剂将单丝黏贴到加强片的两端。制好的试样待黏接剂完全固化后即可开始测试,测试前试样的安装与拉伸试验的相似。
2.2 试样的测试
将试样拉伸至预设的应力水平后,使用手术剪尖端或电火花对纤维中部进行平行切割,然后观察并记录夹紧端的纤维破坏情况以用于压缩强度的计算。纤维上下段的破坏情况主要分四种:上下段均未断裂、上下段单个断裂、上下段均断裂(见图2)。调整预加应力,重复上述实验,获得上下段均未断裂至上下段均断裂的系列预加应力。最后,采用压缩强度计算方法对该系列预加应力进行处理,从而获得碳纤维的压缩强度。测试的关键是预加应力的选择。回弹过程中产生的压应力与破坏时的拉应力大小直接相关。拉应力如果在压缩强度之下,不应观察到回弹压缩破坏;如果大于压缩强度,则能够观察到回弹压缩破坏。有选择地控制拉应力,可以确定回弹压缩破坏的应力阈值,从而获得纤维的压缩强度。
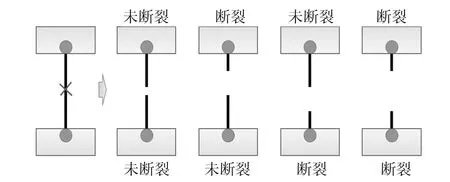
图2 拉伸回弹试验中纤维破坏情况
3 压缩强度的计算方法
拉伸回弹试验无法直接给出单丝的压缩强度。当纤维上下段都断裂时,很难衡量作用于纤维上的回弹应力波比固有压缩强度高多少;同样地,当纤维上下段都未断裂时,也不能确定纤维固有压缩强度比回弹压缩波施加的应力高多少。因此,文献提出了4种统计方法来处理拉伸回弹试验的数据。
(1)极值平均法[8]。首先将施加的应力由小到大进行排列,然后根据纤维上下段的破坏情况,获得上下段均未破坏和均破坏对应的应力,分别作为应力的最小值和最大值,二者的平均值就是该纤维试样的压缩强度。该判定方法直接、清晰,且不需要引入模型进行数据计算,但可能因实验过程的偶然误差,使得试验中纤维上下段均未破坏和均破坏的应力区域变得难以判断的时候,需要进行多次实验,然后求取平均值。
(2)区间择优法[12]。应力以一定范围分区间排列,统计各个应力区间内纤维段破坏的比例,建立该比例与相应应力的线性相关关系。其中,应力区间中最大值和最小值的平均值代表该区间应力值,试样回弹压缩强度就对应于比例为50%时的应力。该方法尤其适用于应用变化范围大的压缩强度测试,缩小应力区间能够获得更为准确的结果。该方法通过图形直观显示了回弹压缩应力的变化,但其基本前提是假设从0~100%破坏是一个连续变化的过程。
(3)Weibull模型与logistic模型。因为纤维的回弹压缩强度破坏数据不符合任何严格的统计分布,因此,需要引入依数据变化而改变分布形态的模型对破坏数据进行描述。G.J.HAYES等[12]基于最弱连接理论提出了Weibull模型,而JIANG H等[16]开发了logistic模型。
根据Weibull模型,累积概率分布函数表述见式(1):
F(σ)=1-e[-L(σ/σ0)m]
(1)
式中:σ为回弹应力,L为标距长度,σ0为与缺陷相关的比例系数,m为与纤维中扭结相关的形状因子。
根据logistic模型,累积概率分布函数表述见式(2):
(2)
式中:a为逻辑曲线的截距,b为回弹应力的回归系数。
这两个应力分布模型被用于对回弹试验数据的拟合,通过每个应力水平下的纤维断裂概率或失效比例的计算,获得了碳纤维的压缩强度。在Weibull模型中,通过双参数拟合,然后推导纤维平均回弹压缩强度;在logistic模型中,确定50%失效时的应力值,从而获得纤维的压缩强度。
I.P.KUMAR等[17]采用上述4种方法计算了碳纤维的压缩强度,具体结果见表1。从表1可知,通过上述4种方法得到的压缩强度差异不明显,最大差值出现在区间择优法和Weibull模型之间,差异仅为16 MPa,仅是所有模型平均压缩强度(869 MPa)的1.8%。

表1 不同计算方法得到的碳纤维压缩强度
4 测试方法的影响因素
计算方法可能影响压缩强度的数值。对于纤维下段,重力作用和弯曲效应是非常明显的,这将导致纤维断裂并非完全来自压缩应力,这增加了模型计算的复杂性[16]。
在测试过程中,纤维切断方式和标距长度是直接影响压缩强度测试结果的主要因素。较早的拉伸回弹实验采用手术剪切断纤维[8],在纤维被切割时,刀片与纤维之间可能发生不对称切割和轴向摩擦,这导致了拉伸回弹应力的不稳定、拉伸应力的异常增加及额外的能量耗散。为了减少系统测试误差,采用电火花瞬时击断纤维[16, 18]。
标距长度是影响测试结果准确性的一个重要因素。当试样长度增加,纤维在测试中容易发生屈曲变形,则压缩破坏可能会发生在屈曲凹面,拉伸形变发生在屈曲凸面,在这种情况下,因为碳纤维拉伸强度通常远高于其压缩强度,纤维断裂需要比轴向压缩时更高的应变能[9]。短标距长度则可能引起夹紧效应,这是因纤维一端被刚性固定所引起,对于各向异性材料来说,夹紧产生的应力的衰减速度非常慢。如果标距长度小于衰减长度,则会在整个试样中产生一些夹紧效应,因此标距长度必须大于衰减长度。通过建立标距长度和压缩强度之间关系,可以消除短标距长度带来的夹紧效应[9],也可以建立含有标距长度的更为通用的logistic模型,从而获得标距为0时的压缩强度[16]。
5 结语
拉伸回弹法是测试脆弹性纤维压缩强度的有效方法。该方法只需借助单丝拉伸试验设备,制样简单,检测过程简便,选择合适的压缩强度计算方法,能够获得可重复的结果。拉伸回弹法在用于评价碳纤维压缩强度时,试样测试与数据计算都非常重要。试样的多次试验能够减小测试结果的偶然误差。通过4种计算方法获得的压缩强度之间差异较小,在评价时可以选择某一种方法作为不同碳纤维试样之间数值的比较。
采用拉伸回弹法用于碳纤维的检测,通过纤维压缩破坏机理和行为的探索,不仅能够为碳纤维微观结构调控提供指导,也能够为纤维在复合材料中的应用提供压缩性能的基础数据。

