基于改进遗传算法的自动控制原理实验考核

肖理庆，储昭霞，王 彬，柴晓宇

(1. 淮南师范学院机械与电气工程学院，安徽 淮南 232038； 2. 淮南师范学院发展规划处，安徽 淮南 232038)

1 引言

为了提高自动控制原理实验教学质量，国内高校积极开展了改革实践。针对电气信息类专业新工科人才培养要求，文献[7]开发了微电机实验平台；针对自动控制原理实验教学现状及改革的必要性，文献[8]提出了多层次实验教学模式；文献[9]结合长期实验课程教学实践，提出了虚拟实验体系。

虽然上述改革实践均有效提高了自动控制原理实验教学质量，但同时存在以下两点不足之处：

1)自动控制原理实验考核反馈的实时性难以满足要求；

2)无法实现自动控制原理实验的差异性考核。

遗传算法作为一种群体型操作算法，被广泛应用于不同优化问题的求解。本文在文献[15]所提出的改进遗传算法基础上，在惯性权重递减策略中引入了指数衰减函数，有效提高了算法的收敛速度与精度。在此基础上，针对上述自动控制原理实验教学改革存在的两点不足之处，自主研发了基于改进遗传算法的自动控制原理实验考核软件，在提高了考核反馈实时性的前提下，实现了差异性考核，达到了“持续改进”的目的。

2 改进遗传算法

2.1 算法简介

所谓改进遗传算法，是指根据随机剖分的变量区间中点适应度函数值和轮盘赌选择生成算法初始种群，并在算法迭代过程中，按概率将粒子群优化算法引入交叉操作中。

为了提高改进遗传算法的寻优性能，首先根据经验知识设置惯性权重的最大值与最小值，然后在按概率引入了粒子群优化算法后，按概率分别采取式(1)-式(5)所示的五种不同递减策略，在算法迭代过程中对惯性权重进行调整，其中采取式(1)的概率值为40，采取式(2)-式(5)的概率值均为15。

(1)

=+(-)·(-)

(2)

=+(-)·(-)

(3)

=+(-)·(-)

(4)

(5)

式中：与分别为迭代次数的最大值与当前值。

2.2 仿真结果

为了对比本文与文献[15]所提出的改进遗传算法性能，现将其分别应用于式(6)-式(11)所示的六种测试函数优化，允许误差设置为10×10，仿真环境和算法其它参数设置均不变，仿真结果分别如图1、表1以及表2所示，其中图1为针对不同测试函数算法平均收敛曲线，表1与表2分别为针对不同测试函数算法收敛精度与收敛代数比较。

(6)

=|sin()+01|+|sin()+01|

(7)

(8)

(9)

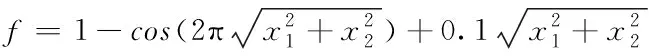
(10)

(11)

图1 针对不同测试函数算法平均收敛曲线

表1 针对不同测试函数算法收敛精度比较

表2 针对不同测试函数算法收敛代数比较

其中：算法1、2分别为文献[15]与本文提出的改进遗传算法。

由图1、表1、表2以及文献[15]可知，在设置改进遗传算法种群数目较少的前提下，应用于式(6)-式(11)所示的六种测试函数优化时，算法1的平均收敛值与平均收敛代数分别为13441×10、69，而算法2的平均收敛值与平均收敛代数分别为27519×10、49。在计算量较小的前提下，本文所提出的改进遗传算法满足自动控制原理实验考核软件对智能算法的要求。

3 自动控制原理实验考核软件

基于改进遗传算法的自动控制原理实验考核软件由基础能力考核和综合能力考核两部分组成，其中基础能力考核部分包含控制系统典型环节模拟电路、典型环节基本连接关系、控制系统稳定性分析、控制系统时域性能指标计算、控制系统根轨迹以及控制系统相对稳定性等六部分，综合能力考核部分为控制系统校正。自动控制原理实验考核软件不仅适用于期末课程实验考核，而且可实现对自动控制原理实验教学过程监控与考核力度的加强。

3.1 基础能力考核

在基础能力考核部分中，首先针对每个设计性实验设置了不同难度系数的考核内容及其对应的时间、分值以及与其它实验的相关性系数等，在此基础上，根据学生所选择的难度系数，以式(12)为适应度函数，利用上述所提出的改进遗传算法确定具体考核内容。

(12)

式中：α、β以及γ均为权值，S与T分别为总分值与总时间，n为考核内容的总数，s与t分别为人为设置的、第i个考核内容的分值与时间，ρ为人为设置的、第i个与第j个考核内容的相关性系数，P为惩罚函数，具体计算方法如式(13)所示。

(13)

式中：D为学生所选择的难度系数，其允许取值范围为0.40-1.00，d与d分别为人为设置的、考核内容难度系数的最小值与最大值，ε为允许误差，其值通常应不超过0.10。

当权值α=β=γ=1、总分值S=60、总时间T=60(分钟)、学生所选择的难度系数D=0.70、允许误差ε=0.10时，上述所提出的改进遗传算法收敛曲线如图2所示，所确定的基础能力考核部分中的考核内容如图3所示。

图2 确定基础能力考核内容时算法收敛曲线

图3 基础能力考核部分中确定的考核内容

由图3可知，根据学生所选择的难度系数和其它设置参数，利用上述所提出的改进遗传算法确定的基础能力考核部分中的考核内容具体为：根据控制系统模拟电路确定其属于何种类型典型环节、补充完整典型环节反馈连接的程序、补充完整赫尔维茨稳定判据的程序、补充完整计算控制系统调节时间的程序、补充完整计算控制系统根轨迹渐近线与实轴交点坐标的程序、补充完整计算控制系统幅值裕度与相角裕度的程序。

在自动控制原理实验考核软件的基础能力考核中，学生可随时交卷，并且在提交试卷后便可查看考核反馈结果，提高了考核反馈的实时性，如图4所示。根据考核反馈结果和当前所选择的难度系数，学生可开展有针对性的复习，掌握之后可选择更高的难度系数，实现“持续改进”。

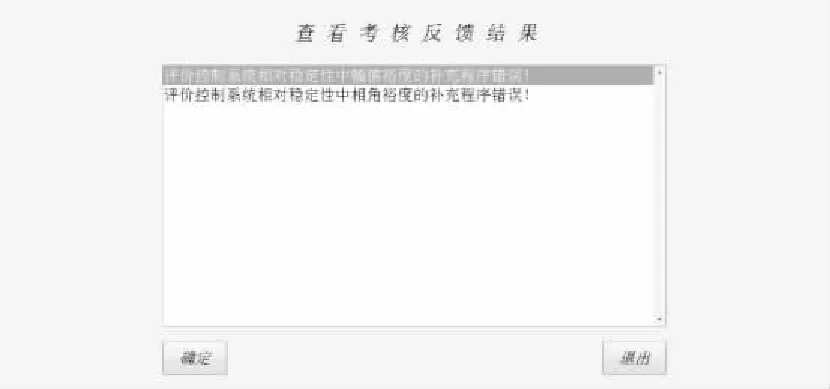
图4 查看考核反馈结果

为了保证最终实验考试成绩的公平与公正，实验考试成绩与软件考核成绩满足式(14)所示关系

(14)

式中：系数η与难度系数D的对应关系如表3所示。另外，在考核补充完整相关程序时，为了避免学生根据题目所显示的参数通过笔算得到对应的结果，自动控制原理实验考核软件采取了“评定所补充程序是否正确时所采用的参数与题目所显示的参数并不相同”的措施。

表3 系数η与难度系数D的对应关系

3.2 综合能力考核

在综合能力考核部分中，首先以式(15)为适应度函数，利用上述所提出的改进遗传算法优化控制器参数，然后根据学生选择的难度系数，确定对采取校正后控制系统各项性能指标的要求。

(15)

式中：t、σ%以及e分别为控制系统调节时间、超调量以及稳态误差。

当权值α=β=γ=100、学生所选择的难度系数D=0.80时，上述所提出的改进遗传算法收敛曲线如图5所示，所确定的综合能力考核部分中的考核内容如图6所示。

图5 确定综合能力考核内容时算法收敛曲线

图6 综合能力考核部分中确定的考核内容

在自动控制原理实验考核软件的综合能力考核中，当学生在比例系数、积分系数以及微分系数对应的方框中分别输入1、0、0时，点击“查看”按钮便可显示采取校正前控制系统的各项性能指标，在此基础上，结合所掌握的控制规律，可不断改变比例系数、积分系数以及微分系数的数值，提交“交卷”按钮便可完成考核，而实验考试成绩与软件考核成绩满足的关系、系数与难度系数的对应关系与基础能力考核时相同。

4 结论

为了提高自动控制原理实验考核的科学性，基于所提出的改进遗传算法，自主研发了包含基础能力考核和综合能力考核的自动控制原理实验考核软件，具有以下特点：

1)所提出的改进遗传算法在惯性权重递减策略中引入了指数衰减函数，在计算量较小的前提下，有效提高了算法收敛速度与精度，满足了自动控制原理实验考核软件对智能算法的要求。

2)在自动控制原理实验考核软件中，根据学生选择的难度系数，利用改进遗传算法分别确定基础能力考核部分中的考核内容和综合能力考核部分中对采取校正后控制系统各项性能指标的要求，实现了差异性考核，达到了“持续改进”的目的。

3)自动控制原理实验考核软件有效提高了考核反馈的实时性。