不确定环境下无人机多目标任务分配问题研究

张力升，郑明发，钟海涛

(空军工程大学基础部，陕西 西安 710051)

1 引言

随着人工智能与飞行器技术的迅速崛起，未来战争正以智能化、无人化的趋势发展，由于其低廉的成本和完善的功能，无人机在军事领域的应用愈加广泛。无人机执行任务过程中，往往存在着多个目标，例如最短航程，最大收益，最小任务执行时间等，这些目标之间往往是相互冲突的，即无法在不牺牲其中某项的同时得到最优，因此，多目标任务分配是无人机作战的关键问题。以往的研究通常是基于确定环境下进行的，文献[4]基于改进粒子群算法对无人机多目标任务分配进行了研究； 文献[5]设计了一种蝗虫仿生算法针对多无人机多目标搜救任务进行研究。这些研究对无人机任务分配的发展都起到了推动作用，然而战场环境复杂多变，我方对于战场情况无法提前检验，有些模型参数信息无法准确描述。为了解决这种问题，最初许多学者采用概率论来进行研究，例如，文献[6]对这种不确定性进行了分析，并通过信息确定性指标来以概率论的方法处理该类问题，文献[7]则是基于SMAA的区间信息条件下解决无人机任务分配问题。但当得到的概率分布足够接近真实频率时才可以概率论。然而实际情况是，由于战场环境动态和复杂的固有特性，无法得到充足的数据甚至有时没有数据，因此，能够获得的样本对于估计一个事件的概率分布来说是很小的。这种情况下，决策者应选择邀请一些军事专家来评估每一个事件发生的信度，而这时应用概率论解决带有专家信度的不确定性问题时会产生与实际情况相悖的结论。那么如何处理这类基于专家信度不确定性的作战任务分配问题呢？ 因此，本文引入了一种新的理论——不确定理论来解决此类问题。不确定理论由刘宝碇教授在2007年创立，并于2010年对其进行完善，它是基于正态性、单调性、自对偶性的一个数学分支，并被广泛应用于各种涉及带有专家信度不确定性的领域。目前，基于不确定理论的不确定规划在研究过程中也得到了迅速的发展。但是在军事作战问题中，研究还不够深入。因此，本文基于不确定理论展开带有专家信度不确定性的无人机任务分配问题研究，采用不确定理论对作战环境中任务分配问题重点不确定因素进行处理，将无人机油耗与毁伤能力描述为不确定变量，建立了不确定多目标无人机任务分配模型； 针对期望值模型没有考虑系统波动性的缺陷，建立了不确定无人机多目标任务分配期望值-标准差模型，从期望值和标准差两个方面考虑了包含不确定变量的目标函数的求解，通过线性加权法与理想点法将多目标问题转化为单目标问题并进行求解，并引入4架无人机，24个目标的任务实例，通过蚁群算法进行求解，得到任务分配的期望值-标准差有效方案，同时对结果进行了简要分析，验证了该方案的有效性和可靠性，最后对今后的研究工作进行了展望，具有一定的理论意义和军事价值。

2 基础知识

不确定测度具备规范性公理、自对偶性公理、次可加性公理及乘积公理，它是不确定理论的基础。

定义21：设为非空集，L为上的一个-代数，事件∈L，为L到[0，1]的一个集函数，若满足：

公理 1(规范性)对于全集，有

{}=1

公理 2(对偶性)对于任何事件，有

{}+{}=1

公理3(次可加性)对于每一个可数序列的事件，可以得到

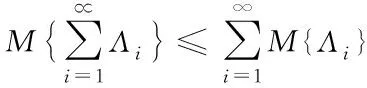
则称为不确定测度，(，L，)被称为一个不确定性空间。

定义22：称为不确定变量，若对任博雷尔集，{∈}={∈|()∈}是L中的一个事件，其中，： (，L，)→为集函数。

定义23：设，，…为实数集的博雷尔子集，若满足

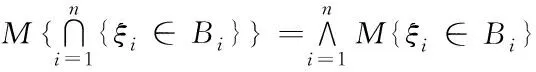
则称不确定变量，，…，相互独立。

定义24：假设为不确定变量，对于∀∈，则称函数()={≤}为的不确定分布。

定义25：假设是一个不确定变量，其不确定分布为，则称()为的逆不确定分布。

定义26：对于不确定变量，定义其期望值为

其中，上式的两个积分至少一个是有限的。

定义27：当不确定变量的分布函数为如下的线性不确定分布：

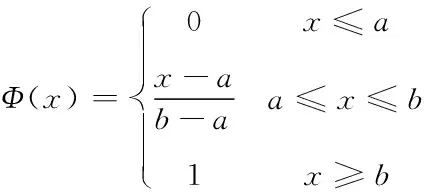
则称为线性不确定变量，记为-(，)，其中，均为实数且<。

定义28：当不确定变量的分布函数为如下的之字型不确定分布

则称为“之”字形不确定变量，记-(，，)，其中，，均为实数且<<。

定义29：对于不确定变量，设其期望值为，则定义的方差[]为

[]=[(-)]

定理21：若不确定变量有其不确定分布，如果其期望值存在，则有

3 不确定多目标无人机任务分配模型

3.1 问题描述

在对需要执行的无人机进攻目标进行明确之后，应当建立详细的进攻任务执行计划。进攻任务规划问题中目标函数涉及到单位油耗以及毁伤能力这些因素，需要领域专家来评估这些具有专家信度不确定性的因素，是随战场实际情况变化的，因此，无人机进攻任务规划问题的目标是不确定的。

3.2 目标函数构建

无人机执行进攻任务时，最重要的是保证任务完成，确保对目标单位的毁伤，实战中并不能像理想条件下实现对目标的确定毁伤，因此在无人机进攻能力和目标单位价值因素的综合影响下，需要建立合理方案以获取最高价值的回报。此外，在执行任务时也要考虑燃油成本，燃料属于重要战略物资，要尽可能减少航程、降低油耗。在这种情况下，将给出如下的目标函数。

1)任务收益目标函数

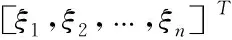
2)燃油代价目标函数

航程即无人机的飞行路程。第架无人机从当前位置前往执行第项任务的航程为，在实际飞行过程中，油耗受航速航高以及天气变化影响较大，因此借助军事专家给出每架无人机的单位油耗记为不确定变量，得到架无人机单位油耗为不确定变量=[，，…]，可以得到燃油代价目标函数为

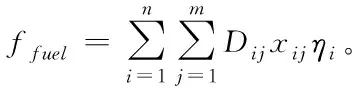
通过上述的目标函数，定义武器毁伤能力和单位油耗为不确定变量，并根据对最大任务价值与最低油耗的考虑，得到如下不确定双目标无人机任务分配模型

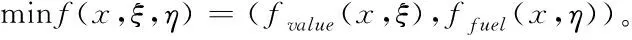
3.3 约束条件建立

在对目标函数进行确立后，下面对约束条件进行分析。由于任务自身要求以及实际战场中无人机自身性能所限制，约束条件可分为协同约束，最大航程两部分，其具体形式如下。

1)任务协同约束

任务协同约束是指对目标的每个任务都只能执行一次，即一个目标不能执行进攻任务多次。即

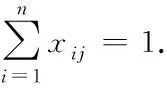
2)最大航程约束

单个无人机执行进攻任务时，最大飞行距离限制了其不能飞行过远距离，只能执行航程内最优进攻任务。即

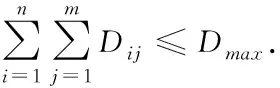
根据上述分析，建立了不确定无人机任务分配问题(Uncertain multi-objective task allocation problem，UMOTAP)模型如下

(1)

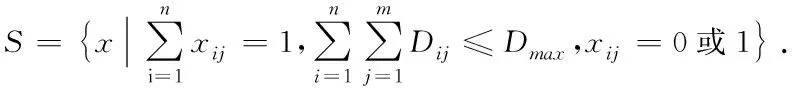
由于目标函数之间的关联性，在实际作战时，仅仅考虑任务收益或航程这一类单个的目标函数是不够全面的，需要对多个目标函数都进行规划。所以，本文建立的模型(1)体现了实际作战需求。

4 问题求解

由于原不确定无人机任务分配问题求解较复杂，本文建立了不确定无人机多目标任务分配期望值-标准差模型，从期望值和标准差两个方面考虑了包含不确定变量的目标函数的求解，通过线性加权法与理想点法将多目标问题转化为单目标问题并进行求解。

4.1 不确定因素的处理

由于UMOTAP模型(1)存在不确定性因素和多目标特征，因此求解存在一定困难。本文首先根据数字特征对UMOTAP模型(1)中的不确定变量进行处理。由于在不确定无人机多目标任务分配中，通常考虑平均收益最大及平均油耗最低，因此从这个角度考虑，采用期望值来描述UMOTAP模型(1)的特征，可以得到如下的任务分配期望值模型

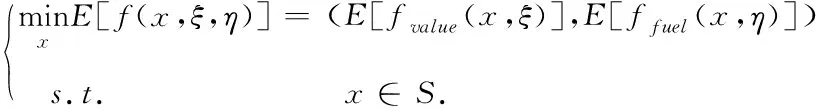
(2)

但因为仅用期望值无法反映问题的波动性，需要通过方差来描述UMOTAP模型(1)，为了计算方便，本文使用标准差。因此，对模型(1)的目标函数分别取期望值和标准差，得到如下含有四个目标的确定任务分配期望值-标准差模型

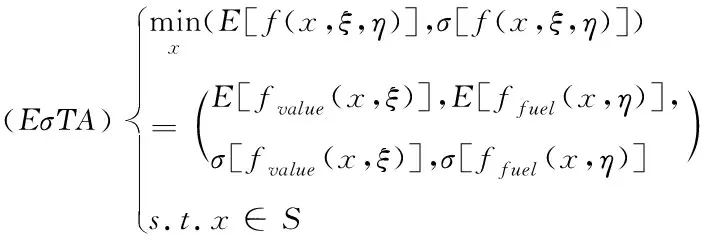
(3)

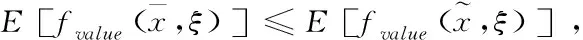
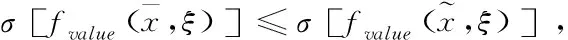
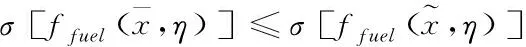
通过从期望值-标准差的角度考虑不确定无人机多目标任务分配问题的有效解，将此问题转化为确定无人机多目标任务分配问题。但由于多目标规划求解较为复杂，本文将其转化为单目标问题进行求解。

4.2 确定多目标无人机任务分配模型求解

在通过期望值-标准差的定义后，原问题就转化为确定无人机多目标任务分配问题。在多目标规划中，通常采用线性加权法与理想点法对多目标问题进行求解，下面给出两种求解方法。

4.2.1 线性加权法

在多目标规划问题中，线性加权法是常见方法之一，其思想是由于每个目标的重要程度不同，因此通过赋予权值并求和来构造新的目标函数，将确定多目标无人机任务分配问题转化为确定单目标无人机任务分配问题：

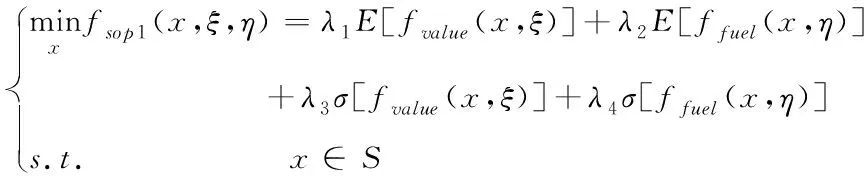
(4)

其中

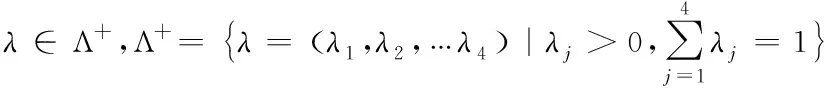
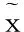
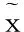
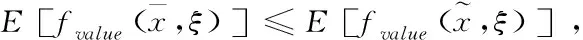
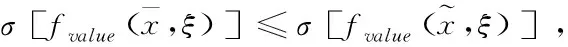
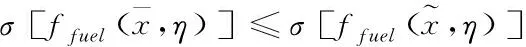
且上述四式中至少存在一个是严格小于的，又因∈，所以存在

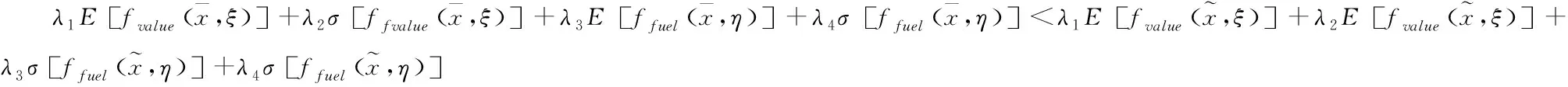
由此可得

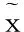
4.2.1 理想点法

在决策过程中，每个目标都有一个较为理想的预期值，称为理想点，当所有目标都达到理想点时，可以得到理想最优方案，但事实上这是无法完成的，退而求其次，最接近理想点的方案就是最优方案。理想点法的思想就是通过最小化目标实际值与理想点的距离函数来求解的，是将原始的确定多目标任务分配问题转化为确定单目标任务分配问题，转化方法是通过最小化距离函数来实现的

(5)

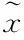
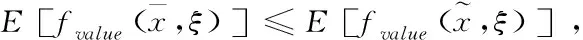
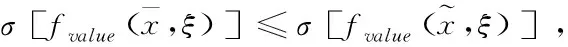
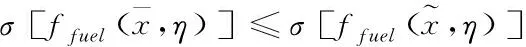
且上述四式至少存在一个是严格小于的，使得

因此可以得到

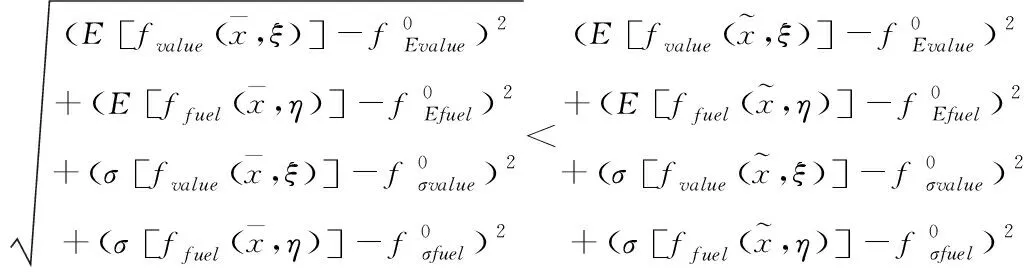
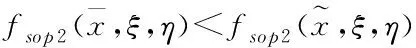
4.3 蚁群算法求解

虽然转化为单目标，但由于模型规模较大，求解任务分配最优方案仍较难，因此本文引入蚁群算法对模型进行求解。蚁群算法(AG)是一种模拟蚂蚁觅食行为的模拟优化算法，它是由意大利学者Dorigo M等人于1991年首先提出，并首先使用在解决TSP(旅行商问题)上。该算法通过蚁群在搜索食物源的过程中所体现出来的寻优能力来解决一些系统优化中的困难问题，算法的基本思想是模仿蚂蚁依赖信息素的机制，通过蚂蚁间信息素强度的正反馈的方法来引导每个蚂蚁的行动。

多目标蚁群算法的流程如下：

1)初始化参数

初始化时间和循环次数，设置最大循环次数为G，初始化路径信息素，将其置为常数c。

2)构造解空间

将m个蚂蚁置于n个元素上，依照概率进行周游并记录最佳路线。

3)更新信息素

获得每条路径上新的信息量，更新禁忌表与信息表。

4)迭代寻优

判定是否满足结束条件，即达到最大循环次数后结束循环并输出优化结果，否则清空禁忌表并继续循环。

算法具体流程如图1所示。

图1 蚁群算法流程图

4.4 数值例子

为了对算法内容进行演示，下面通过一个数值例子的详细求解对算法效果进行测试，设置测试函数表达式为(，)=sin*sin，极大值点位于(0，0)处，极大值为1。设定初始参数：最大循环次数为50，信息素重要程度因子为=1，启发函数重要程度因子=5，信息素强度=50，信息素挥发因子=01。

该算法对测试函数进行优化后，优化曲线如图所示。在迭代30次后基本接近最大极值1。

图2 测试函数求解结果

5 仿真实例

下面通过实例求解来分析本文所建立不确定多目标无人机任务分配模型以及求解方法的有效性及可靠性。仿真中假设有4架无人机对24个目标执行进攻任务。无人机基地所在坐标为(30，2)，飞行最大距离为=[200，180，175，188]，无人机任务目标坐标如表1。

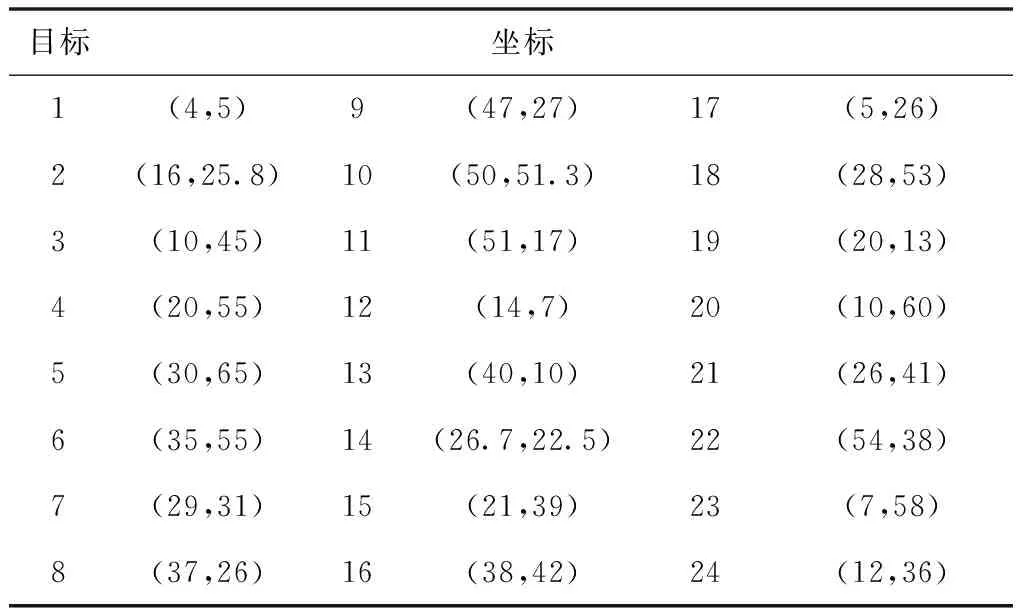
表1 目标所在位置

仿真中最大循环次数为4000，信息素重要程度因子为=1，启发函数重要程度因子=5，信息素强度=50，信息素挥发因子=01。

由于无法准确获知敌目标防空能力，在实战中武器对目标的毁伤能力是不确定的，经专家估计将武器对目标的毁伤能力=(，，)的四个分量定义为之字形不确定变量，记～(3，4，5)，～(2，3，4)，～(1，2，3)，～(2，3，5)，其分布函数如定义28所示，因此可以得到任务收益目标函数。因为天气影响，航行油耗也是一个不确定变量，经专家估计将实际飞行油耗=(，，，)的四个分量定义为线性不确定变量，均记为～(300，360)，其分布函数如定义27所示，并得到期望值标准差有效解定义下的燃油消耗目标函数。同时在对不确定变量进行处理后，将原问题转化为单目标规划问题，并通过蚁群算法进行寻优，得到在满足目标函数下的期望值有效解。

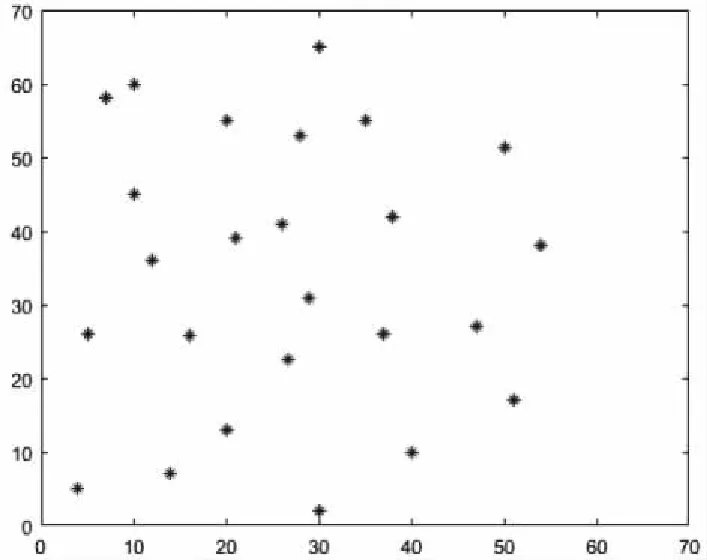
图3 任务目标坐标

通过计算得到的无人机任务分配结果与飞行里程如表2所示。

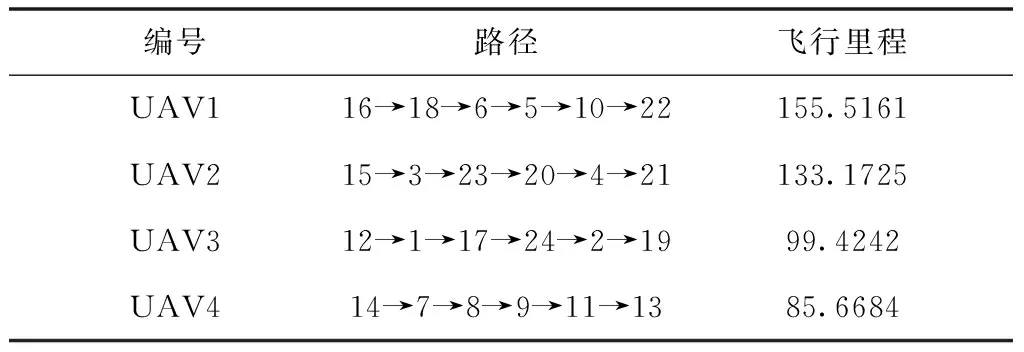
表2 无人机飞行路径及飞行里程

通过数据迭代过程可以看出，引入蚁群算法对模型进行求解，在经过了60次迭代过后就收敛至最优解，且在进行多次迭代后，求解结果都相对稳定，算法求解效果较好； 根据得到的分配方案计算可知总航程距离为473，与期望值模型进行对比后可以发现，目标函数值有一定降低，且本模型具有更好的稳定性，而期望值模型没有考虑系统的波动性，不能完全胜任战场实际情况。综上，按本文建立的不确定无人机多目标任务分配模型来规划无人机进攻任务并通过不确定理论进行求解，可以较好地完成战场不确定环境下的对敌进攻任务。

图4 任务分配路径

6 结束语

本文对不确定多目标无人机进攻任务分配模型进行了分析，针对其不足引入了不确定理论，给出了不确定变量确定方法，对于解决实际空战中的无人机进攻任务分配提供了一个可行的方案。下一步，可以引入协同任务，进一步研究不确定多目标无人机协同任务分配，使模型更贴近实战，实用性更高。