冰粒磨料射流冰粒加速规律及破碎煤岩数值模拟

黄 飞，焦杨洋，米建宇，李树清，赵志旗，刘 勇

(1.湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室，湖南 湘潭 411201；2.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411201；3.河南理工大学 河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地，河南 焦作 454003)

水射流割缝技术作为煤层增透抽采瓦斯的有效途径之一，为预防煤与瓦斯突出、高效抽采煤层气做出了卓越贡献。其中，磨料水射流通过磨料的高速磨削作用，大幅提升了射流破碎煤岩的性能，在煤层割缝领域受到了广泛的青睐。然而，通过大量工程实践发现，传统的高压磨料水射流煤层割缝技术由于大量磨料颗粒(诸如石榴石、陶粒、石英等)的掺入带来了一系列的问题：① 残留磨料颗粒广泛分布在割缝后的缝槽与裂隙内部，极容易堵塞瓦斯渗流通道；② 沿壁面残留分布的磨料颗粒增加了孔壁的摩擦阻力，容易导致卡钻抱死等问题。因此，寻求一种既能增加射流冲击破碎煤岩性能、又能有效避免上述问题的新型磨料射流成为该技术广泛应用的瓶颈难题。文献[4-5]研究发现，将冰块破碎成细小颗粒后混入高压水射流能有效进行物料清洗和表面除锈，这种新型射流被称之为冰粒磨料射流。在相同工况下冰粒磨料射流的冲击性能几乎媲美常规磨料射流，且冰粒冲击靶体后迅速融化可有效规避传统磨料带来的问题。由此可见，采用冰粒磨料水射流代替传统磨料水射流进行煤层割缝有望发挥磨料射流的磨削冲击性能，同时避免传统磨料射流带来的堵塞渗流通道与卡钻等问题。作为一种新型的磨料水射流技术，冰粒磨料射流冲击性能的强弱是判定该技术能否有效破碎煤岩的关键，是该技术能否成功应用于煤层割缝的重要参数。针对高压磨料射流冲击下煤岩体的破碎规律问题，目前已有大量的文献开展了研究。黄飞等通过大量的冲击试验研究了磨料水射流冲击下具有层状节理岩石的多尺度破碎形态。米建宇等采用SPH-FEM耦合算法模拟了后混合磨料水射流冲击破碎岩石的规律，探讨了冲击压力、磨料浓度与围压等因素对岩石破碎的影响规律。黄中伟等提出一种新型的液氮磨料射流，并开展了液氮磨料射流喷射高温花岗岩室内实验。刘勇等对比分析了磨料水射流与磨料气体射流的破岩压力，并基于统一强度理论构建了适用于磨料射流破岩的能量准则。刘送永等采用数值模拟手段研究了在有围压存在的情况下磨料射流的破岩规律，探讨了不同大小围压对岩石破碎的影响。上述文献表明，传统磨料射流通过高速磨料的磨削作用与高速流体的冲刷作用，可以提升射流的冲击破岩性能。然而，鉴于冰粒磨料的物性特征与常规磨料区别较大，其掺入射流后的动能大小与冲击破岩规律都将与常规磨料射流有所差异。针对该方面的问题，目前鲜有文献开展研究。因此，笔者拟开展冰粒磨料加速规律的理论推导，在此基础上采用数值模拟的方法研究冰粒磨料射流的破碎煤岩规律。

1 冰粒磨料加速规律理论研究

根据冰粒磨料的掺入方式，可将冰粒磨料射流分为前混合与后混合冰粒磨料射流。其中，后混合磨料射流是将破碎的冰粒从喷腔直接引入，从而在高速水流的卷携作用下获得加速。在此过程中，细小冰粒受到温度较高且速度极快水流的冲刷作用，极易融化。因此后混合冰粒磨料射流对于喷嘴内的低温环境要求极为严格。目前，大多采用预混合的方式来制备冰粒磨料射流，即先将破碎冰粒与一部分冷却水进行充分预混合，然后再掺入高速流体进行加速。冰粒获得加速的过程几乎都是在高压管路中进行，最后高速冰粒磨料与水的混合流体在喷嘴中进行整形与束能后从喷嘴喷出。因此，本文后续所提到的冰粒磨料射流均是指预先混合的冰粒磨料射流。

1.1 冰粒磨料的受力分析

鉴于冰粒磨料的密度、硬度与水介质的亲疏性以及冰粒消融等特性与常规磨料射流差异极大，因此冰粒磨料的加速规律对其最终的冲击速度影响较大，并最终影响其冲击动能的大小。

冰粒磨料的受力与加速过程极其复杂，为了方便推导其加速过程，笔者作如下假设：① 冰粒磨料加速过程主要发生在高压管路内；② 冰粒磨料在高压管路内的运动为一维流动；③ 冰粒之间不发生碰撞，且不影响水的流动；④ 高压水在管路内的流动为定常流，且水温保持恒定；⑤ 冰粒磨料为规则的球形颗粒，冰粒的温度保持恒定，鉴于冰粒与高压水环境之间的温差恒定，本文假设冰粒的消融过程遵循线性消融规律，即球形冰粒的粒径随时间呈线性减小的趋势。

=+

(1)

式中，为冰粒初始粒径；为冰粒运动时间；为冰粒融化粒径；对应为时刻时间节点；为冰粒随时间的消融常数。

根据上述假设可知冰粒的加速过程主要发生在高压管路内，依据文献[18-19]可获得冰粒在高压管路内的主要受力情况如下：

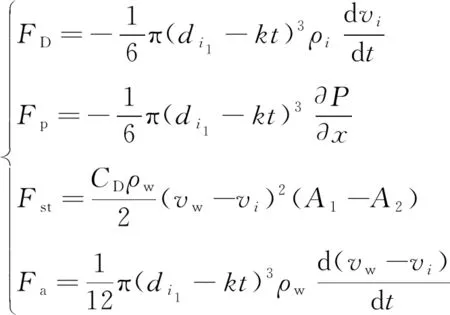
(2)

其中，为惯性力；为压差力；为Stokes阻力；为附加质量力；为冰粒密度；为冰粒速度；∂∂为压力梯度；为阻力系数；为射流密度；为射流速度；为冰粒初始面积；为冰粒融化面积。根据冰粒磨料在高压管道内的运动特征可以推导出冰粒的平衡方程为

+++=0

(3)

将式(1)，(2)代入式(3)可以推导出冰粒磨料的加速度为

(4)

鉴于高速流体在高压管路内的速度基本保持不变，流体的沿程动能损失可以忽略不计。依据伯努利方程可知=0。因此，式(4)可简化为

(5)

1.2 冰粒磨料加速案例分析

依据微积分思想将冰粒磨料的运动时间切分成部分，冰粒磨料在第个微元时间段Δ内的加速度可视为常数。因此可以推导出冰粒磨料从时间节点到+1时的速度变化公式为

+1=+Δ

(6)

已知冰粒磨料的初速度为0，将式(5)代入式(6)便可计算出冰粒的速度表达式为

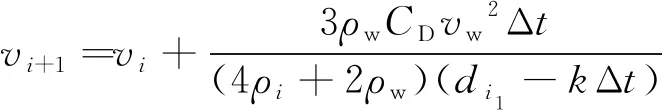
(7)

按照高压管路内流速恒定的假设，射流的速度可表示为

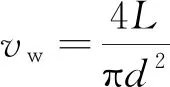
(8)

其中，为管道内的流量，L/min；为管道的直径；m。本文参照了常规前混合磨料射流发生装置的相关参数，选取了流量、管径阻力系数等射流参数，依据冰粒本身的物性选取了冰粒磨料参数，冰粒粒径消融常数主要参考了文献[16-17]，详细参数见表1。基于式(6)～(8)编制计算程序，采用Matlab软件进行迭代计算，获得冰粒磨料的速度与加速度的变化规律如图1所示。

表1 高压管路中所用计算参数

冰粒磨料的加速度变化趋势可以间接反映其在喷嘴内的受力情况。从图1所示的冰粒磨料加速度在高压管路内的变化曲线可知，冰粒磨料的加速大致可以分为3个阶段：从冰粒磨料掺入高压流体的高压管路位置开始至0.14 m范围段为冰粒磨料加速的第1阶段，该阶段的加速度迅速增加至峰值；从0.14～0.8 m范围段为冰粒加速的第2阶段，该阶段的加速度从峰值呈指数形式急剧减小；从高压管路内0.8 m位置至喷嘴出口的范围段为冰粒加速的第3阶段，该阶段的加速度减小的趋势变缓并逐渐趋于稳定。根据冰粒磨料的加速度变化规律可以推测，冰粒磨料掺入高压射流后的受力加速过程非常短暂，且主要集中在第1，2阶段。

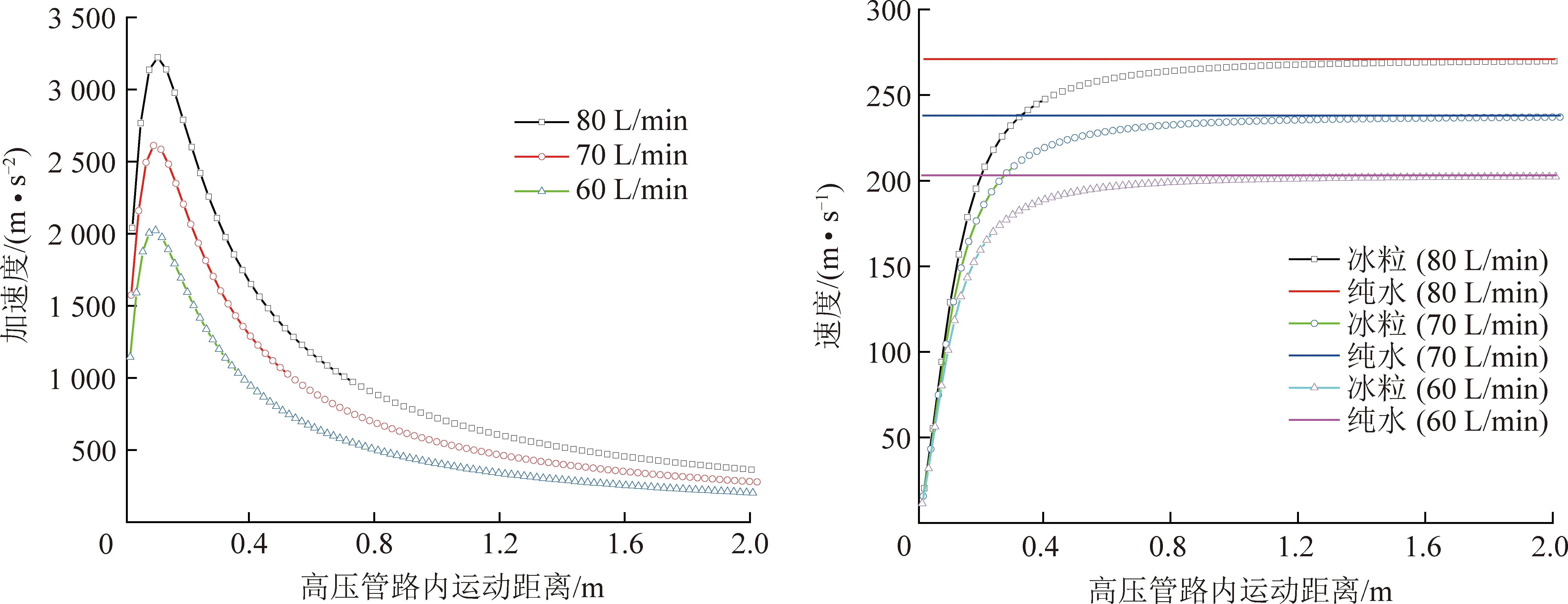
图1 不同流量下冰粒磨料的加速度与速度变化曲线

通过对比常规磨料射流的加速度变化规律发现，常规磨料的加速度通常只有第2、第3阶段，表明常规磨料一旦掺入高压流体后其获得的受力和加速度即达到峰值，随后便逐渐减小。进一步分析表明，冰粒磨料的加速度之所以出现短暂的增加趋势，主要是考虑了冰粒消融导致其粒径逐渐减小，根据式(4)可知在较短时间内冰粒受力变化较小，而冰粒的粒径有所减小，因此其加速度出现增加的趋势；当达到峰值加速度后，冰粒受力急剧减小，此时虽然冰粒粒径也按照式(1)的趋势减小，但其减小幅度逐渐小于受力减小的幅度，加速度出现减小趋势。

另一方面，根据冰粒磨料的速度变化曲线可知，冰粒磨料在混入高压射流后，其速度急剧增加，约1 ms后速度增加的趋势变缓并逐渐趋近于水的速度，最后与高压水一起从喷嘴喷出形成高压冰粒磨料射流。根据冰粒磨料的加速度和速度变化规律可知，鉴于冰粒的特殊性能获得很好的加速过程，最终喷出速度几乎可以接近水的速度，从而能够极大地提升冰粒磨料射流的冲击动能。

2 冰粒磨料射流冲击破岩模型构建

2.1 SPH-FEM耦合方法

SPH-FEM的耦合主要采用罚函数法使质点的力作用在有限元上，从而实现SPH与有限元的耦合。在计算过程中，粒子与有限元表面保持接触，避免穿透。如果粒子穿透了有限元表面，则粒子的位置和速度根据以下等式进行调整：

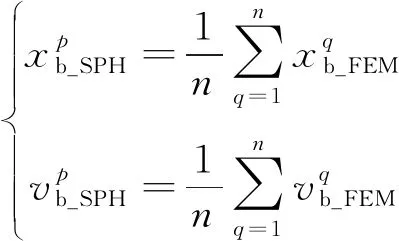
(9)

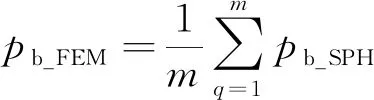
(10)

式中，为界面上有限元的压力；为单元中心附近的粒子压力；为元素中心附近的粒子数。

2.2 水的本构模型

笔者采用Null材料模型并赋予其状态方程Mie-Grueisen，该状态方程可表述为

(11)

其中，为流体所受的压力；为水的初始密度；为水的黏滞系数；为单位体积内能；为质点速度与声波速度(-)曲线截距；，与为-曲线斜率系数；为Grueisen常数；为一介体积修正量。笔者选取表2所示的材料参数来模拟水的本构关系。

表2 水的本构模型参数

2.3 冰的本构模型

笔者只考虑高速冲击下冰的力学行为，因此采用CARNEY等所提出的本构模型来描述冰粒磨料。该本构模型不仅考虑了冰的拉伸屈服强度和压缩屈服强度，而且还考虑了冰在拉伸状态和压缩状态下的应变率效应。

(12)

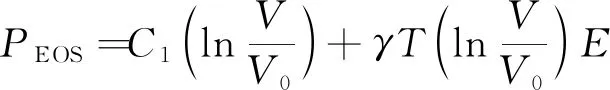
(13)

式中，为冰的参考体积；为冰的体积；与分别为冰的压缩与拉伸参数；为系数。

此外，该本构模型考虑了拉伸和压缩过程中冰粒的阶段压力，计算公式为

(14)

表3 冰的材料参数

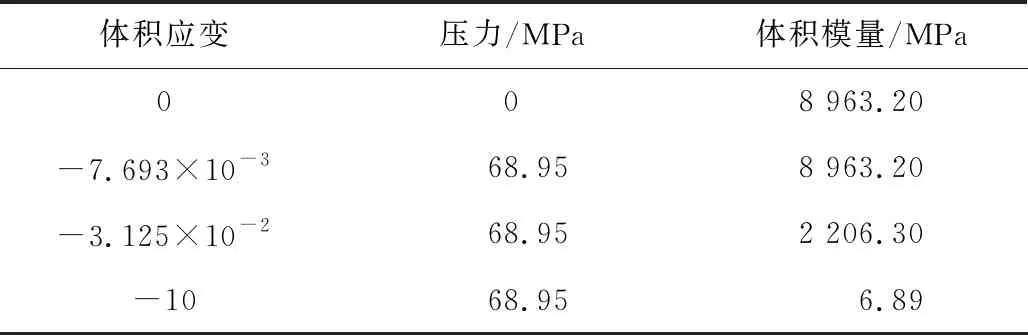
表4 冰的状态方程参数

2.4 煤的本构模型

笔者采用HJC本构模型来模拟高速冰粒磨料射流冲击下的煤岩，详细材料参数见表5。其中，为煤岩密度；为单轴抗压强度；为最大静水抗拉强度；为剪切模量；为规范化最大强度；为允许塑性应变；为压垮静水压力；为压垮体积应力；为压垮体积应变；为极限体积应变；，，，，，，，，为材料常数；为参考应变率。

表5 煤的本构参数

2.5 几何模型构建与速度赋值

为了便于统计冰粒磨料浓度对射流冲击破煤的影响规律，笔者将水与冰粒磨料采用SPH方法构建，将煤块采用FEM方法构建。为了模拟真实的磨料在水中随机分布的情况，采取如下建模方法：

第1步，建立一个磨料水射流圆柱几何模型，在该几何模型中按照体积分数比分别建立纯水SPH模型和冰粒磨料SPH模型。

第2步，建立好2段SPH模型后，提取2段SPH粒子在空间中的坐标信息，然后采用随机函数编程将2段SPH的坐标信息打乱，从而实现冰粒磨料在水射流中的随机分布。构建的冰粒磨料射流冲击破碎煤块的几何模型如图2所示。

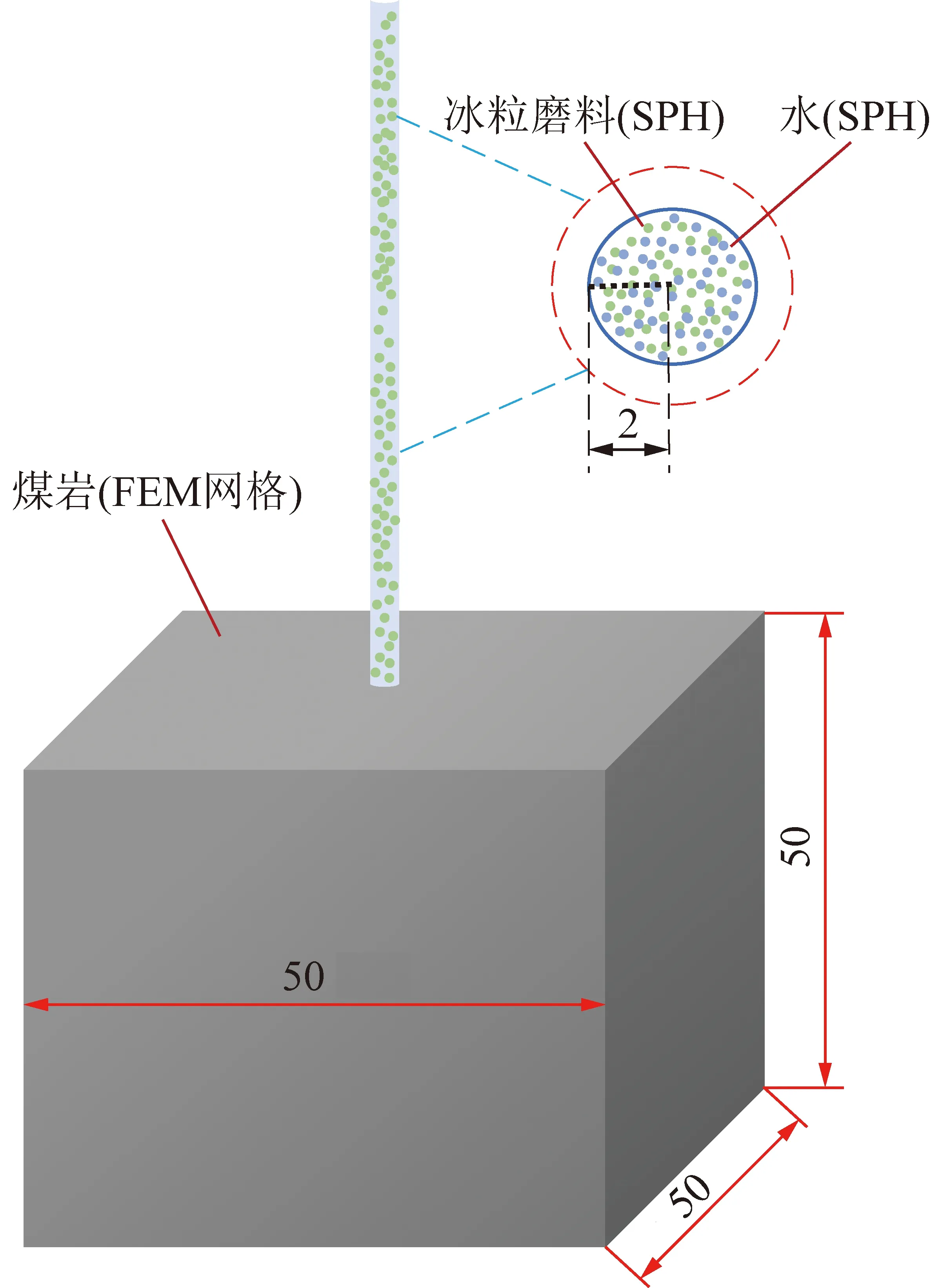
图2 冰粒磨料水射流冲击煤岩模型

根据2.4节的理论研究结果可知，冰粒磨料与纯水介质从喷嘴喷出时，两者的速度几乎相同。本文忽略2个速度间的微小差异，将冰粒磨料与纯水介质设置为相同的初速度进行模拟计算。

3 冰粒磨料射流破碎煤块效果分析

按照上述方法建立数值模型，然后采用LS-DYNA进行模拟计算。图3为冰粒磨料射流冲击破碎煤块的时间序列。从图3可以看出，在冰粒磨料射流的冲击下，煤块中心形成V型的破碎坑，破碎坑外围出现不同程度的损伤。随着冲击时间的增加，破碎坑持续向煤块深部发展，损伤范围也相应扩大。上述煤岩破碎现象与现有大量文献获得的破岩规律几乎一致，表明本文所建立的数值计算模型具有一定可靠性。

图3 煤岩损伤时序

另一方面，从图3可以看出，当冰粒磨料高速冲击煤岩后，部分冰粒迅速融化并转换为液态的SPH水介质。这一现象与实际冰粒磨料射流冲击煤岩后的消融规律相符，进一步表明本文所建立的冰粒磨料射流冲击破碎煤岩的可行性。

为了定量获取煤块在冰粒磨料射流冲击下的损伤规律，本文以煤岩受冲击中心为基点，沿模型轴方向截取煤岩的1/2剖面，沿中心轴向下分别设置压力监测点1号与应力监测点2号，记录所选监测点损伤随时间的变化。此外，在距中心轴15 mm的径向距离范围内连续选择38个损伤监测点，标记为3～40号，并记录这38个监测点的最终损伤。同样的，沿轴轴向距离处选取40个损伤监测点标记为41～80号，以探究煤岩在3种水射流冲击下的损伤范围，详细的监测点布局如图4所示。

图4 监测点布置示意

3.1 不同速度冰粒磨料射流破碎煤块规律

为探究冰粒磨料射流速度对煤岩损伤规律的影响，笔者选取了速度分别为300，400，500，600，700，800，900 m/s的冰粒磨料射流进行破岩试验，冰粒体积分数为12.5%，设置冲击时间为2 s，不考虑围压作用。计算完成后提取了部分煤岩的损伤云图，如图5所示。由图5可知，随着射流速度的增大，煤岩V型破碎坑体积增大，破碎坑附近的损伤范围也随之增大。

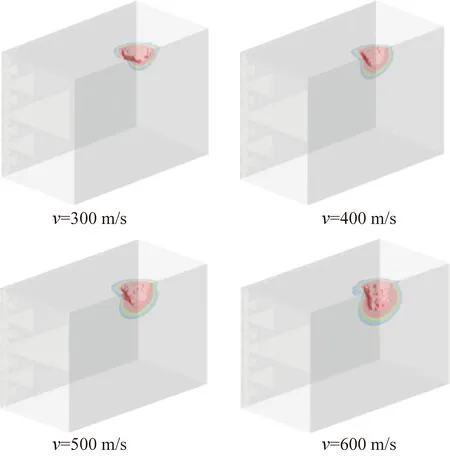
图5 不同速度冲击下煤岩损伤云图

为了定量获取射流速度对煤岩宏观破碎坑的影响规律，笔者采用软件提取了煤岩的破碎深度与破碎深度数据，并绘制了两者随射流速度的变化关系，如图6所示。从图6可以看出，随着射流速度的增加，煤岩的破碎深度呈现近似线性增长的趋势。当冰粒磨料射流速度为300 m/s时，煤块的最大破碎深度约为7.5 mm；当冰粒磨料射流速度增加至900 m/s时，煤块的最大破碎深度达到了约30 mm。反观煤块的破碎宽度出现了不同的变化趋势。具体来说，当冰粒磨料射流速度在300～500 m/s时，煤块破碎深度随速度增加呈现小幅度的增加趋势；当冰粒磨料射流速度进一步增大，破碎宽度不再随速度增加而有明显的增加趋势。分析研究表明，冰粒磨料射流速度增加，其冲击动能=/2呈倍数关系增加，导致煤块受到的冲击能量增加，最终其破碎深度线性增加。然而，随着冰粒磨料速度的增加，其冲击磨削性能得到提升，从而能更好地磨削煤块形成更加完整的切口，促使冲击破碎向煤块内部发展，而破碎宽度不再增加；另一方面，冰粒磨料射流的直径不变，阻碍了破碎宽度的进一步扩展。

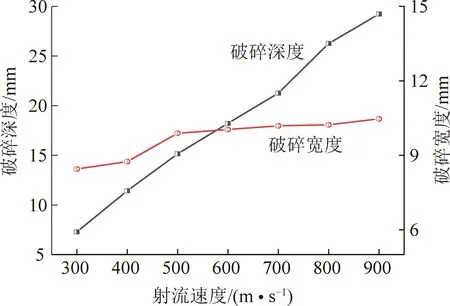
图6 射流速度与破碎宽度和深度的关系

此外，为了掌握不同速度的冰粒磨料射流冲击下煤块的损伤发展规律，提取监测点41～80号的损伤值，并绘制了不同速度下煤岩的损伤曲线，如图7所示。定义损伤的取值范围为0～1，其中，0代表没有受到损伤，具体表现为网格单元未有任何形变；1代表煤块被剥离，具体表现为单元网格出现大变形并达到损伤极限后被删除。根据上述定义可知，煤块纵向破碎坑的最大深度即损伤值为1时对应的纵向距离，而煤块损伤的最大深度即损伤值为0时对应的纵向距离。

根据图7所示，通过计算获得如下关系式：

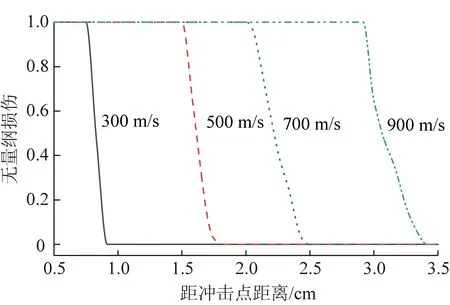
图7 不同射流速度下煤岩损伤范围

(15)

其中，Δ为纵向相对损伤增量，Δ=(-)/×100%，%。根据式(15)可以看出，冰粒磨料射流冲击下，煤块的纵向损伤增量保持在(0.129～0.133)内，且与冰粒磨料的速度没有明显关系。由此推测，冰粒磨料射流冲击煤岩的最大损伤深度约为破碎坑深度的1.13倍。

3.2 不同体积分数冰粒磨料射流破碎煤岩规律

为研究冰粒磨料体积分数对煤岩损伤规律的影响，笔者选取了冰粒磨料的体积分数分别为0，12.5%，25.0%，37.5%，50.0%，进行破岩数值模拟试验，射流速度为400 m/s，设置冲击时间为2 s，不考虑围压作用。计算完成后提取了各冰粒体积分数下煤块的破碎与损伤云图，如图8所示。当纯水射流中加入体积分数为12.5%的冰粒磨料后，煤岩的破碎坑体积与损伤范围明显增大；然而，随着冰粒磨料体积分数的继续增加，煤岩破碎与损伤的范围变化不明显。根据上述结果可以推测，冰粒磨料的掺入能够明显提升射流冲击破碎煤岩的性能。

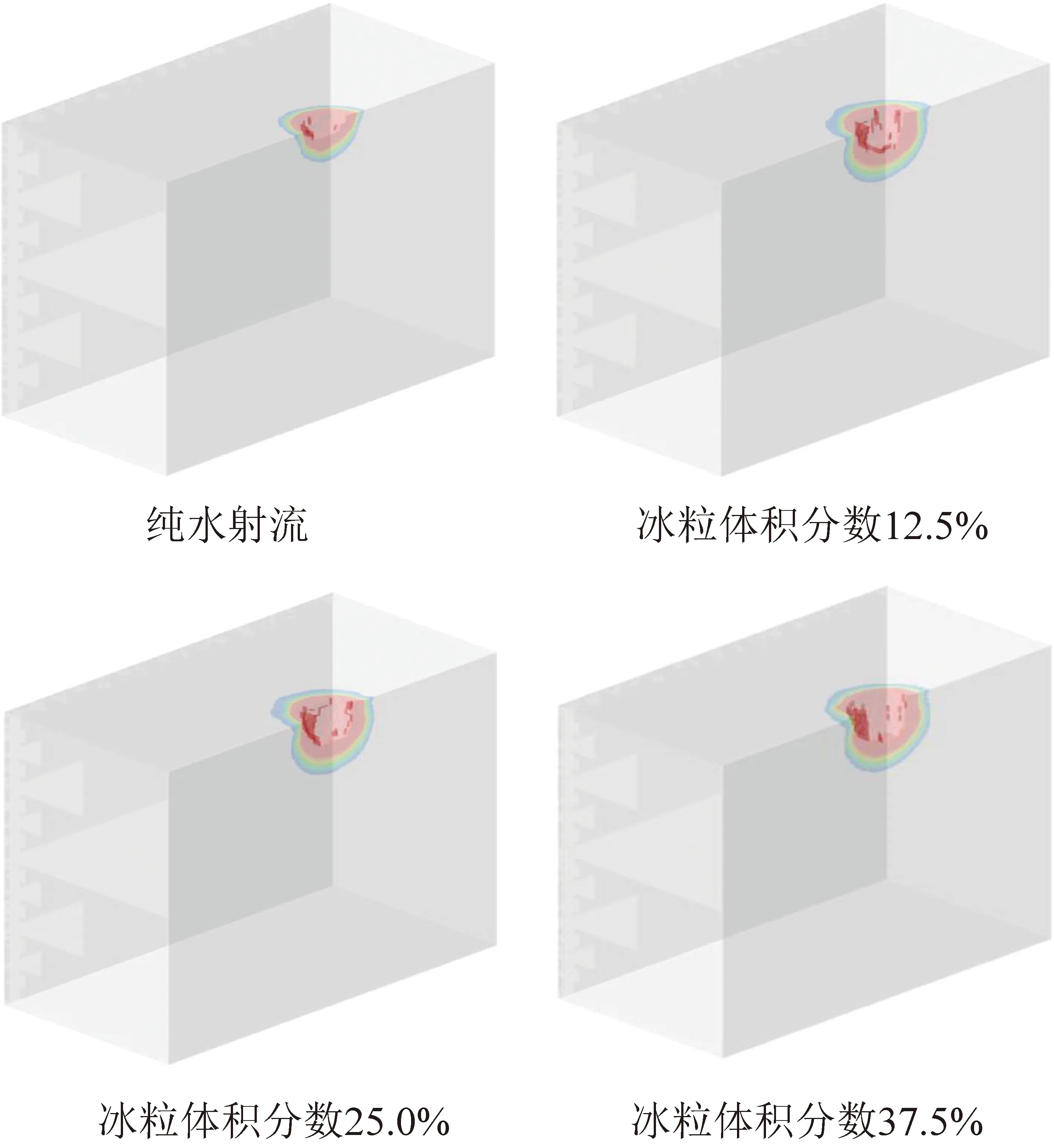
图8 不同磨料体积分数下煤岩损伤云图

为了定量研究冰粒体积分数对煤岩宏观破碎坑的影响规律，依次提取了不同冰粒体积分数下煤岩的破碎深度与破碎宽度数据，并绘制了2者随射流速度的变化曲线，如图9所示。

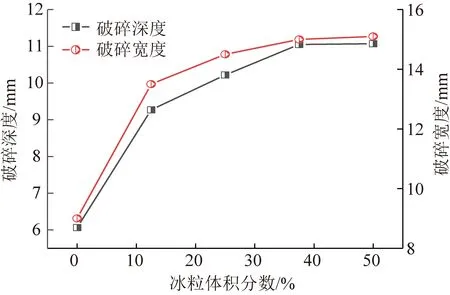
图9 磨料浓度与破碎宽度和深度的关系

由图9可知，在相同工况下的纯水射流中掺入12.5%的冰粒磨料后，煤岩破碎坑的最大深度由约6 mm增加至约9.4 mm，增幅约为56.7%；破碎坑宽度由约9.6 mm增加至约13.6 mm，增幅约为41.7%。继续增加冰粒体积分数至37.5%，煤岩破碎坑的最大深度约为11 mm，增幅约为17%；破碎坑宽度约为14.8 mm，增幅约为8.8%。继续增加冰粒体积分数，煤岩破碎坑的最大深度和宽度几乎不再增加。分析认为，出现上述变化趋势的主要原因是纯水射流与冰粒磨料射流冲击破岩的作用不同。纯水射流主要借助高速流体的水锤压力和滞止压力的冲刷作用破碎煤岩，而掺入冰粒磨料后，冰粒的磨削与切削作用主导了破岩作用，更加有利于煤岩的破碎。因此，在纯水射流中掺入冰粒磨料后煤岩的破碎深度和宽度都大幅增加。由此可以推测，针对特定物性参数的煤岩体，存在一个破碎效果最佳的冰粒磨料体积分数。

为了进一步了解冰粒体积分数对煤岩损伤宽度的影响规律，提取监测点3～40号的损伤值，并绘制了如图10所示的损伤曲线。同理定义破碎坑的宽度为损伤值为1时对应的横向距离，损伤的最大宽度为损伤值为0时对应的横向距离。根据图10进行计算获得如下关系式：

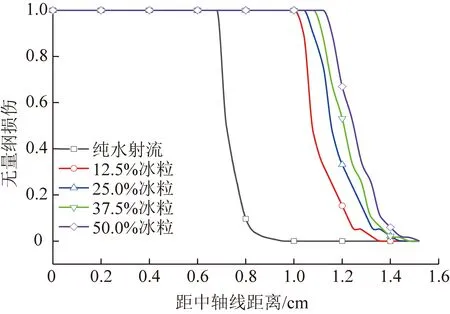
图10 不同体积分数冰粒下煤岩损伤范围

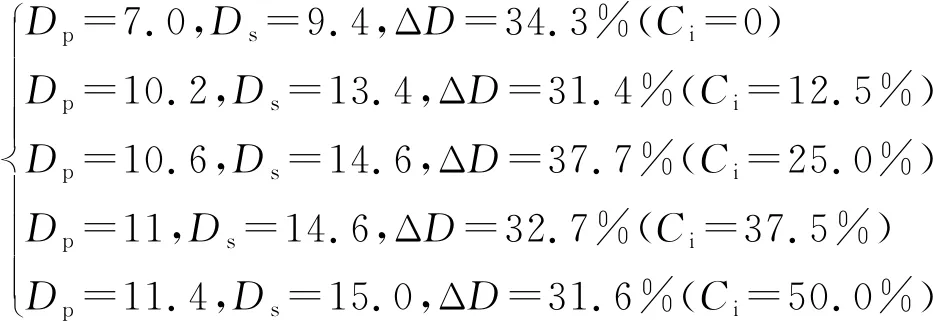
(16)

其中，为冰粒磨料的体积分数，%；Δ为横向相对损伤增量，Δ=(-)/×100%，%。根据式(16)可以看出，在磨料射流的冲击下，煤岩横向损伤直径约为破碎坑直径的1.3倍。

3.3 不同围压下冰粒磨料射流破碎煤岩规律

在具体的煤层割缝实践中，煤岩均处于高围压限制约束状态。为了使本数值模拟更加贴合工程实际，在数值模型中对煤岩4个侧面均施加相同的压力，模拟煤岩受到的围压状态，分别对煤岩施加1，2，3，4，5，6，7，8，10 MPa的围压进行计算，选取射流速度为400 m/s，冰粒体积分数为12.5%，设置冲击时间为2 s。计算完成后，同样提取部分煤岩损伤云图，如图11所示。

从图11可以看出，煤岩的破碎与损伤范围随着围压的增加出现明显减小的趋势。

图11 不同围压状态下煤岩损伤云图

通过软件提取破碎深度与宽度，并绘制2者随围压的变化曲线如图12所示。从图12可以看出，在冰粒磨料射流冲击下，煤岩的纵向破碎深度由无围压时的约15.2 mm降低至1 MPa围压时的13.1 mm；继续增加围压，纵向破碎深度呈近似线性的趋势减小。然而，煤岩的横向破碎宽度随着围压的变化始终在9.9 mm上下波动，未有表现出随围压而变化的趋势。通过上述现象可知，在冰粒磨料射流冲击下，围压阻碍了煤岩的纵向破碎损伤，但是对于横向的破碎损伤没有影响。

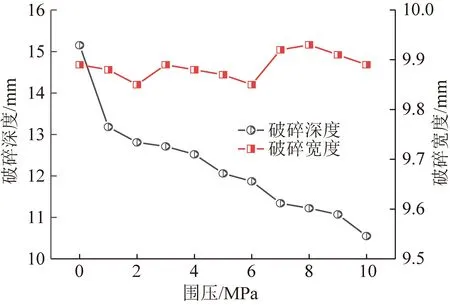
图12 围压与破碎宽度和深度的关系

提取监测点41号在不同围压条件下的损伤随时间的变化数据，并绘制该点的时序损伤，如图13所示。从图13可以看出，随着围压的增加，煤岩在冰粒磨料射流冲击下的损伤明显受到了抑制作用，具体表现为围压越大，损伤需要的时间越长、损伤的程度越小。另外，从图13还可看出，在冰粒磨料射流冲击下，煤岩的损伤几乎是阶梯状发展的。分析认为，这可能是由于煤岩被逐次剥离从而露出新的接触面所导致的。

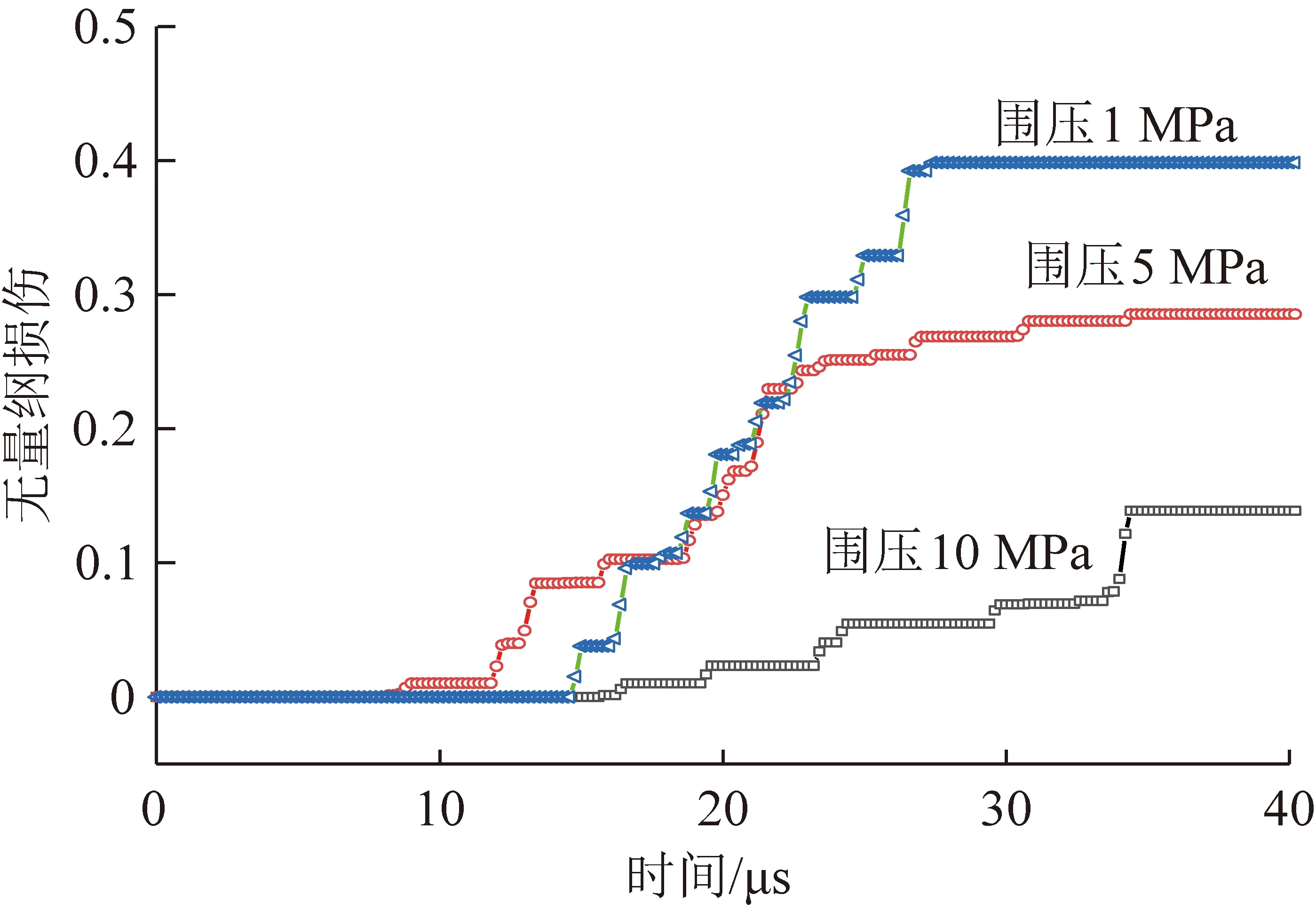
图13 不同围压下煤岩的时序损伤

4 结 论

(1)冰粒磨料掺入高速流体后在高压管路内获得了先增大后减小的加速度，最终其速度几乎接近纯水速度，为后续数值模拟中冰粒磨料和纯水的速度赋值提供了依据。

(2)冰粒磨料在冲击煤岩前后出现消融现象，且煤岩出现V型破碎形态，表明本文所构建的冰粒磨料射流破碎煤岩的数值模型具可行性。

(3)煤岩纵向破碎深度随冰粒磨料射流速度的增加而线性增加，而横向破碎宽度随速度呈现先增加后趋于稳定的变化趋势，煤岩纵向损伤深度约为纵向破碎深度的1.13倍；冰粒磨料掺入纯水射流后，煤岩的纵向破碎深度和横向破碎宽度均出现了大幅增加，随着冰粒磨料体积分数的增加，破碎深度和破碎宽度增加的趋势变缓，最后煤岩横向损伤直径约为横向破碎宽度的1.3倍；围压越大纵向破碎深度越小，表明煤岩所受围压极大地抑制了其在冰粒磨料射流冲击下的纵向破碎深度。